表面粗糙度信号的统计误差特征分析

王焕玲 / 福建省计量科学研究院

表面粗糙度信号的统计误差特征分析

王焕玲 / 福建省计量科学研究院

根据最小二乘法原理对表面粗糙度信号统计误差进行了分析，并绘制了最小二乘法统计直方图。研究成果表明，表面粗糙度信号统计误差近似服从正态分布。由matlab做出的数组normal plot函数图形以及误差统计学中的皮尔逊χ2检验法进一步验证了表面粗糙度误差信号的正态性分布特征。

表面粗糙度；误差信号；统计特征；最小二乘法；正态分布

0 引言

随着现代社会经济的迅猛发展，机械工业对加工零件的表面质量提出了更高的要求，表面粗糙度就是衡量加工工件表面质量的重要指标之一。表面粗糙度反映的是机械零件表面的微观几何形状误差，其准确度极大地影响加工工件的使用性能，因此快速准确地测量出表面粗糙度成为现代社会机械工业的迫切需要［1-2］。

以往一些发达国家如德国、美国、英国的国家标准中都采用了中线制作为表面粗糙度参数的评定方法。具体参数千差万别，但主要评定参数有Ra、Rz和Ry，这也是国际间交流最常用的一些参数。随着当今微机处理技术、集成电路技术的发展，出现了时序分析法、最小二乘多项式拟合法、滤波法、分形法、Motif法、功能参数集法等各种评定方法，取得了诸多进展，但是它们只能得到真实表面的有限信息，仍然存在一些问题有待完善，如缺乏表面粗糙度误差信号统计特征的全面准确描述。

对某一工件进行表面粗糙度测量，并对其误差信号的正态特性分析是本文的主要研究问题。通过对测量信号加以提取分析，从各个方面分析影响测量结果的因素。分析结果表明，表面粗糙度误差近似符合正态分布。最后对其正态分布利用皮尔逊检验法进行检验，总结影响表面粗糙度误差正态分布的因素。研究发现，实验提取数据点数是其主要因素，从而提出最优提取原则，以采用科学有效的方案提取被测表面粗糙度的特征信息。根据国家标准GB/T 4881-2001《数据的统计处理和解释 正态性检验》，当对观测值是否服从正态分布存在疑问时，使用偏离正态分布的检验是有用的，甚至是必须的。该标准中偏离正态分布的检验是针对非分组的原始数据，而不是分组数据，而χ2拟合优度检验仅适用于分组数据。为研究表面粗糙度误差信号的统计特性，本文采用误差统计学中的皮尔逊χ2检验法，最终得出表面粗糙度信号误差确实服从正态分布规律，并且表面粗糙度误差模型和提取点数有一定的必然关系。

1 表面粗糙度误差分析

表面粗糙度测量常用的方法有比较法、触针法、光切法和干涉法［3］。通过综合考虑本文采用触针法。国家标准规定采用中线制评定表面粗糙度，粗糙度的评定参数一般从Ra、Rz、Ry中选取，并且优先选用Ra，故在本文中表面粗糙度误差选取的是参数。

1.1 表面粗糙度误差的最小二乘中线评定模型

根据触针法测量表面粗糙度的原理，触针在被测表面滑出一条直线。选5个0.8 mm的取样长度，总评定长度4 mm，总取点数4 000点，即得到4 000个Ra参数，根据最小二乘法得到表面粗糙度误差的最小二乘中线。最小二乘法是评定形位误差最常用的方法之一，具有计算简单、适用性广的特点。最小二乘评定的基本思想是：寻找一理想要素，使已测得的实际要素各点相对于该理想要素的偏差平方和为最小，并将由此得到的最大极差作为评定的误差值［5-6］。在测量过程中，被测对象坐标x轴跟坐标测量x轴基本是一致的，设测量采样数据为（xi， yi），i = 1， 2， …， N，建立坐标系xoy，x轴代表采样点顺序，y轴代表测量得到的数据，如图1所示。

图1 最小二乘法示意图

假定最小二乘直线（即理想直线）的方程为

式中：a——最小二乘直线的斜率，待定系数；

b——最小二乘直线y轴的截距，待定系数则各采样点（xi，yi）相对于该理想直线的距离即为偏差值εi：

偏差的平方和为

依据最小二乘原理，应有：

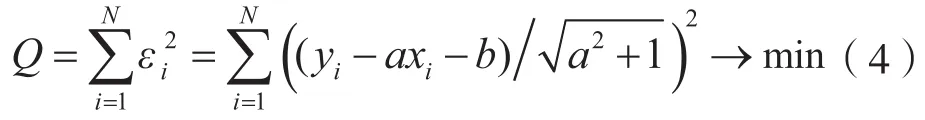
1.2 表面粗糙度误差统计分析

为了更全面地了解表面粗糙度误差的特征，根据误差产生的随机性对其进行统计分析。

1.2.1 表面粗糙度误差最小二乘中线拟合统计分析

通过编程把实验数据导入MATLAB软件，根据最小二乘原理拟合出计算表面粗糙度误差参数Ra的基准中线［8］，并绘出根据最小二乘法转换坐标系后各点的统计分布图（图2）和误差分布图（图3）。图2中横轴代表误差，纵轴代表出现的次数。图3中横轴代表被测物件的长度，纵轴代表误差，即距离基准中线的距离。

实现的具体工作流程如图4所示。

图2 最小二乘法转换坐标后点的分布

图3 最小二乘法转换坐标系后的误差分布

图4 最小二乘中线实现流程

1.2.2 表面粗糙度粗大误差的剔除

在一列重复测量数据中，有个别数据与其他数据有明显差异，它可能是含有粗大误差的数据，称为可疑数据。它会对测量结果产生明显的歪曲，因此从测量结果中剔除粗大误差是必要的。

判别粗大误差最常用方法是莱依达法则，即3σ准则［5-6］。该法则是以测得数据均为正态分布为前提，采用逐步剔出法判别测量数列中是否包含粗大误差。在实际测量中常以标准偏差s代替σ，以测量平均值代替真值。对某个可疑数据，若其满足，则剔除xd。剔除粗大误差后的最小二乘法转换坐标后的统计直方图如图5所示。图5中横轴代表误差，纵轴代表出现的次数。

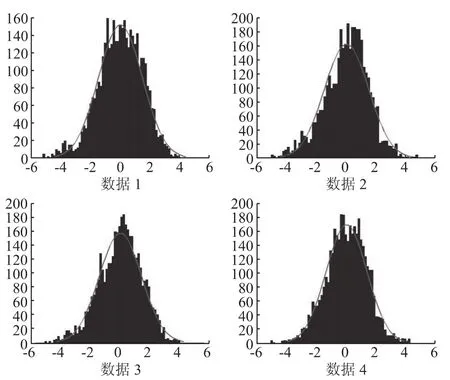
图5 剔除粗大误差后的最小二乘法转换坐标后点的分布

2 表面粗糙度统计误差正态性检验

由以上表面粗糙度误差最小二乘统计直方图可以看出，表面粗糙度误差近似服从正态分布，下面验证其正态性分布。

2.1 表面粗糙度误差的normplot统计绘图函数分析

在MATLAB中做出数组的normal plot函数图形，若落在直线上的数据点越多，则表示该组数据越符合正态分布［9-10］。一般地，中间的点离直线位置偏差不能过大，两头的点的偏差可以允许大一些。图6是本研究中四组图形的normalplot函数图形，图中横坐标代表概率区间，纵坐标代表概率分布。从图6可以看出，除了第二组数据落在直线外的数据点稍多外，每组数据大部分的数据点都落在直线上，因此，可以基本确定表面粗糙度统计误差是服从于正态分布的。

图6 误差的normplot函数图形

2.2 表面粗糙度统计误差正态性特征的验证

表面粗糙度统计误差正态性特征的检验方法步骤如下［6］：

2）将搜集到的样本资料进行组距式分组，并得到实际频数。

3）对各组组距进行标准化处理，并计算出各组的概率。

4）用样本容量乘以各组的概率，得到各组的理论频数。

5）进行检验：

（1）提出假设：H0服从正态分布，H1不服从正态分布；

（3）给定显著性水平α，确定临界值；

（4）作出结论，是接受正态分布原假设还是拒绝原假设。

四组数据的检验结果如表1所示。

表1 检验结果

由表1可知，以上四组数据检验结果都不符合正态分布，并且第二组的χ2系数明显大于其他三组数据。由四组normplot统计函数图而知，皮尔逊检验确实有一定的可信性。与其他检验方法对比，皮尔逊检验法要求样本数量至少为50，D检验法中明确提出样本数量在51～1 000之间，所以提出假设，是不是因为数量过大导致皮尔逊检验法失效。于是分别在各组数据中随机提取了100、300、500、600、800、1 000、1 050、1 125、1 250、1 500、2 000个数据点重新进行皮尔逊检验，每一组实验点数都随机选10次来做重复试验，并取平均值作为最终χ2的值，再与标准的χ2值进行对比，检验结果如表2～表5所示。

由表2～表5可以看出，第二组数据明显不符合正态分布，而其他三组数据提取点数在1 000左右时基本都符合正态分布，而且在提取500左右数据点时正态性最佳。

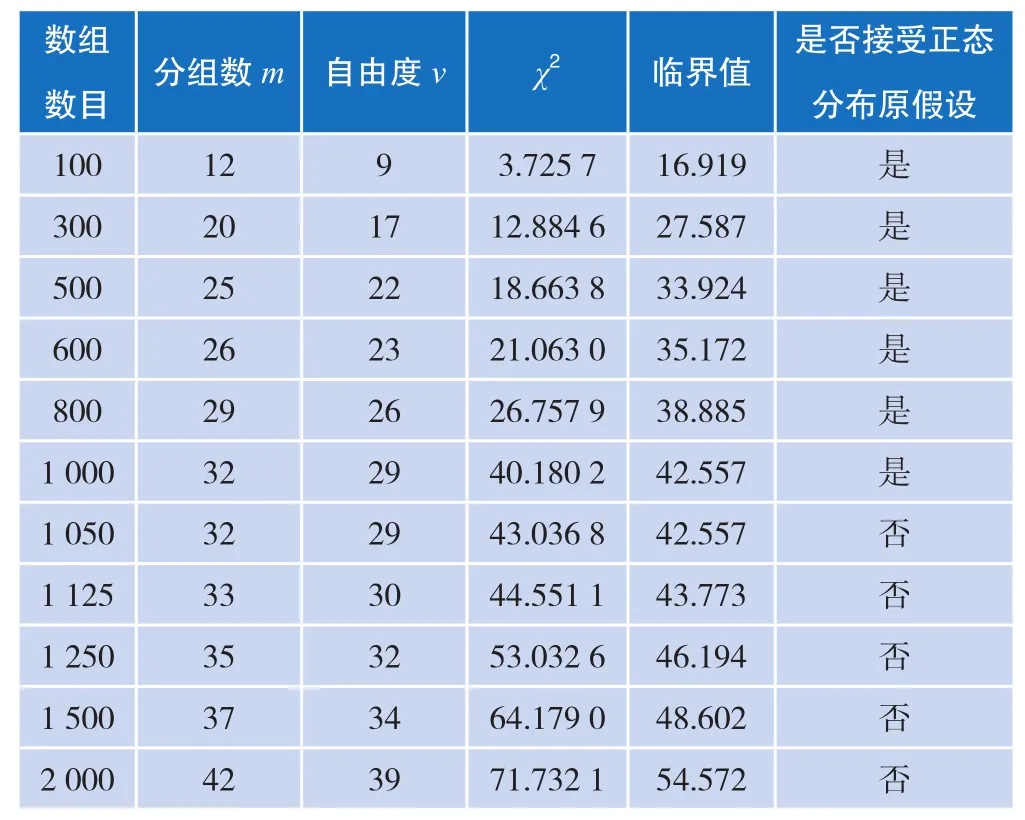
表2 数据1 处理结果表（显著性水平α = 0.05）

表3 数据2处理结果表（显著性水平α = 0.05）

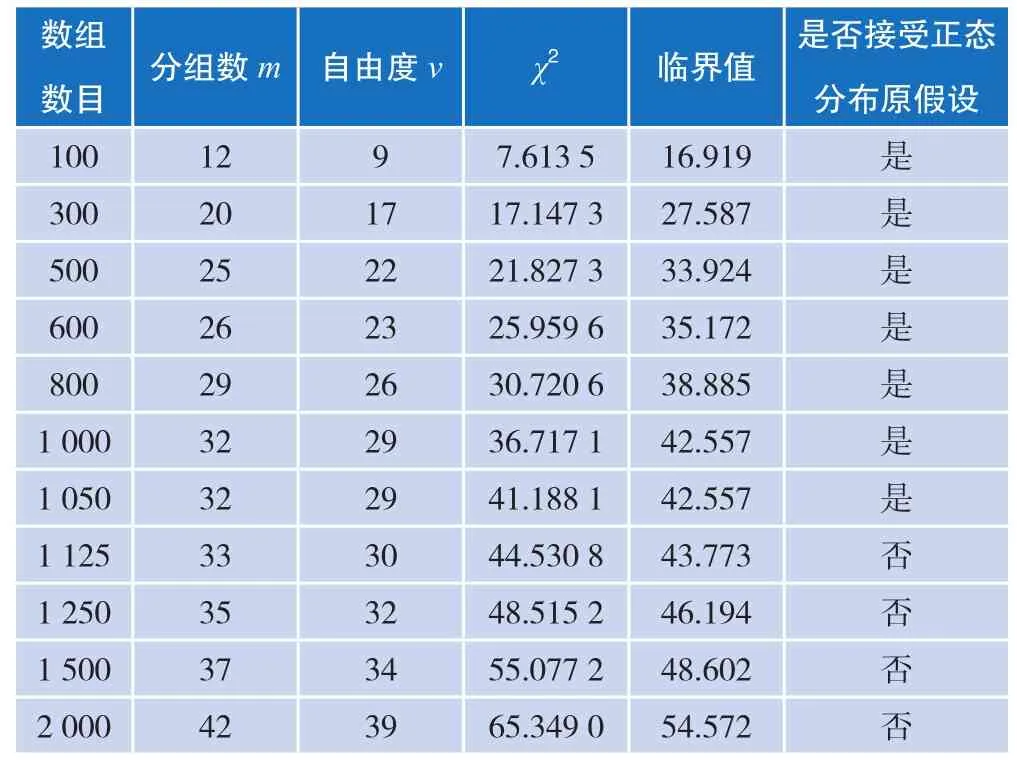
表4 数据3处理结果表（显著性水平α = 0.05）

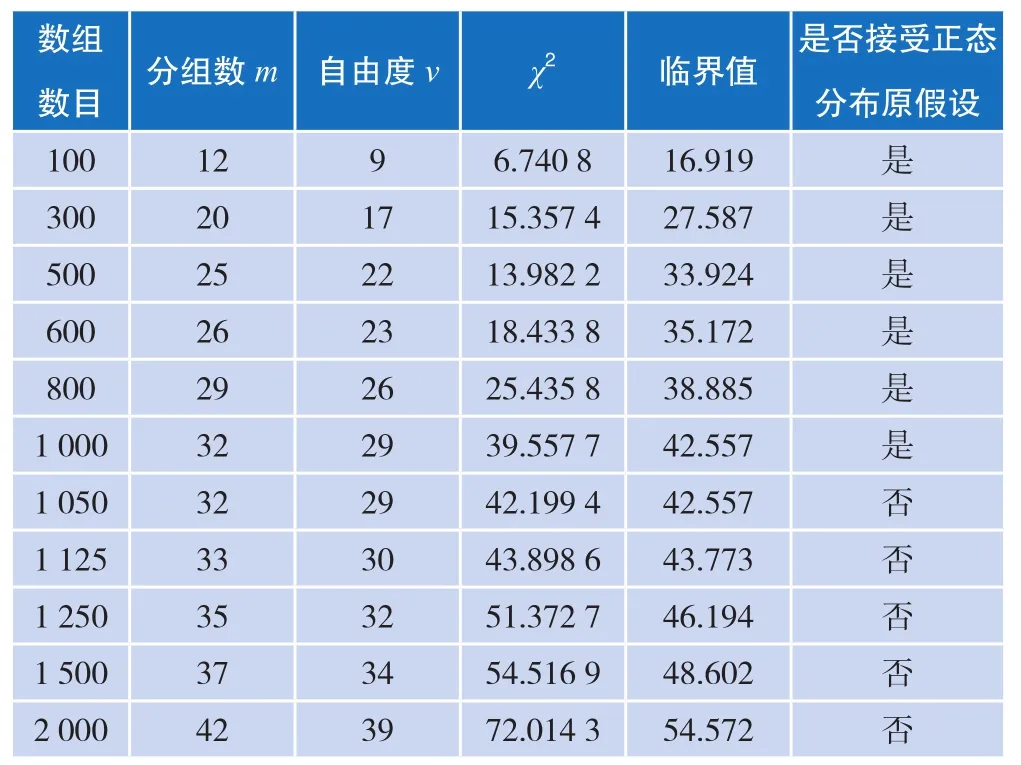
表5 数据4处理结果表（显著性水平α = 0.05）

3 实验结论及分析总结

实验结论：经过皮尔逊检验，数据1、3、4误差分布服从正态分布，数据2不符合。

通过对本实验的初步分析可得出：皮尔逊检验的使用范围样本数应小于等于1 000；在运用皮尔逊假设检验法检验数据时，分组和合并组后，应保证实际频数最多的区间频数不能大于实际频数最小的区间，否则会导致的结果很大，致使检验失效，所以可得出结论：皮尔逊检验需针对不同的样本数量，应对分组后的各组频数进行限定。针对此观点，大样本数据如果要求各组实际频数不相差过大，也必然会使分组数增加，进而大于理论分组数，这与检验原则相悖。

4 结语

本文通过对表面粗糙度误差正态分布特性及正态性检验的研究，得出表面粗糙度误差近似符合正态性分布的结论。特别值得强调的是，在检验正态特性分布时采取了皮尔逊检验法。通过实验探索了表面粗糙度误差特征模型与提取点数之间存在的必然关系，最终得出数据提取点数在1 000左右时基本都符合正态分布，而且在提取500左右数据点时正态性最佳。本文的初步研究成果对于表面粗糙度检测的整个过程完善具有非常重要的科学意义，同时为其他统计误差特征识别项目的研究打下了良好的基础。

［1］杨练根，曹丽娟，宫爱红. 互换性与技术测量［M］. 武汉：华中科技大学出版社，2010.

［2］马宏，王金波. 仪器精度理论［M］. 北京：北京理工大学出版社，2009.

［3］刘斌，冯其波，匡萃方. 表面粗糙度测量方法综述［J］. 光学仪器学报，2004（5）：54-58.

［4］王宏伟. 表面粗糙度的测量与数据处理［J］. 科技信息，2009（35）：738.

［5］沙定国. 误差分析与测量不确定度评定［M］. 北京：中国计量出版社，2003.

［6］费业泰，陈晓怀，秦岚. 误差理论与数据处理［M］. 北京：机械工业出版社，2010.

［7］徐红兵. 几何量公差与检测试验指导书，2版［M］. 北京：化学工业出版社，1992.

［8］刘志平，石英林. 最小二乘原理及其MATLAB实现［M］. 北京：高等教育出版社，2001.

［9］朱旭，李换琴，籍万新. MATLAB软件与基础数学实验［M］. 西安：西安交通大学出版社，2008.

［10］周品，赵新芬. MATLAB 数理统计分析［M］.北京：国防工业出版社，2009.

The analysis of statistical error characteristics of the surface roughnesssignal

Wang Huanling
（Measurement Science Research Institute of Fujian Province）

According to the principle of least square method the statistical error characteristics of surface roughness signal are analyzed， and statistical histograms of least square method are drawn.The research results indicate that the statistical errors of surface roughness signal obey the normal distribution similarly. The normal plot function graphs of array made by matlaband Pearson χ2test method of the error statistics further verify the normal distribution characteristic of surface roughness error signals.

surface roughness； error signal； statistical characteristic； least square method； normal distribution