基于AHP-TOPSIS模型的岩土边坡稳定性评价

姜廷文，靳春玲

（兰州交通大学土木工程学院，甘肃 兰州 730070）

基于AHP-TOPSIS模型的岩土边坡稳定性评价

姜廷文，靳春玲

（兰州交通大学土木工程学院，甘肃 兰州 730070）

选用岩石质量指标、岩体完整性指标、地应力、黏聚力、内摩擦角、坡高和日最大降水量7个影响因素作为边坡稳定性评价指标，采用改进的层次分析法（AH P）计算各评价指标的权向量，结合逼近理想解排序法 （TOPSIS）构建改进的AH P-TOPSIS模型。依据单指标等级分类区间的下限构造5个不同等级的临界值边坡，将其稳定性指标临界值与4组边坡稳定性指标实测数据一同代入AH P-TOPSIS评判模型，通过计算它们与理想解的贴进度来划分稳定性等级分类区间，进而与4组待评价边坡贴进度对比确定出边坡稳定性等级。研究结果表明，采用AH P-TOPSIS模型对边坡稳定性的评价结果与灰色关联法和可拓评价法等结果基本相符，证明该模型的可行性，为边坡稳定性评价提供了一种新的分析方法。

边坡；稳定性评价；改进的AH P；AH P-TOPSIS模型

0　引言

在铁路、公路、水利、建筑及矿山等工程项目中，岩土边坡的稳定性对工程选址、工程质量、工程耐久性及工程安全性有直接和间接的影响［1］，合理地评价边坡稳定性对工程项目具有重要意义。由于边坡稳定性影响因素的复杂性和不确定性，传统的单指标或少数指标评价方法会遗漏重要信息，不能够全面准确地评价边坡的稳定［2，3］。为了适应边坡稳定性影响因素的特征，大量文献已提出了不确定性指标的评价模型，如模糊数学方法［4，5］、灰关联分析方法［6］、因子分析法［7］、人工神经网络法［8，9］及可拓评价法［10，11］等。这些方法都有各自的侧重点和优势，但也存在一定的缺陷。例如，传统的模糊分析方法计算复杂，对指标权重矢量的确定主观性较大；人工神经网络法虽克服了权重确定的主观性，但应用中需要大量的实际学习样本，而样本获取较为困难；因子分析法把多个指标中的大部分信息浓缩到少数几个指标中，使浓缩后因子的意义不能完全确定，而且会有一些信息未被提取。

为此，结合岩土边坡稳定性影响因素的特点，本文采用改进的3标度层次分析法（anal yt i c hi erarchy process，AH P）和逼近理想解排序法［12］（TOPSIS）相结合应用于稳定性评价中。考虑到传统的9标度层次分析法中对判断矩阵一致性检验的问题，采用3标度层次分析法降低权重确定的主观性，避免了一致性检验，减少计算量，提高了计算精度，并且把多目标决策理论中的TOPSIS引入岩土边坡稳定性评价中，构成AH P-TOPSIS综合评价模型，为岩土边坡稳定性评价提供了一种新思路。

1　改进的AH P法及权重确定步骤

1.1改进的AHP法

层次分析法（AH P）是将决策总是有关的元素分解成目标、准则、方案等层次，在此基础之上进行定性和定量分析的决策方法。该方法是美国运筹学家匹茨堡大学教授萨蒂于20世纪70年代初提出的一种层次权重决策分析方法。改进的3标度AH P法是将同一层的指标两两比较，改变传统9标度法中9种判断原则，通过3种判断原则确定其相对重要性，从而减小和避免多原则判断主观性造成的误差［13］。

1.2权重确定的步骤

1.2.1构造比较矩阵

假定指标集Z=｛z1，z2，…，zn｝，其中，zi为第i个评价指标（i=1，2，…，n），n为评价指标总数。用3标度原则对评价指标两两对比，构造的比较矩阵为

其中3标度矩阵含义见表1。

表1　3标度矩阵含义

1.2.2将比较矩阵A转化为最优传递矩阵

最优传递矩阵为

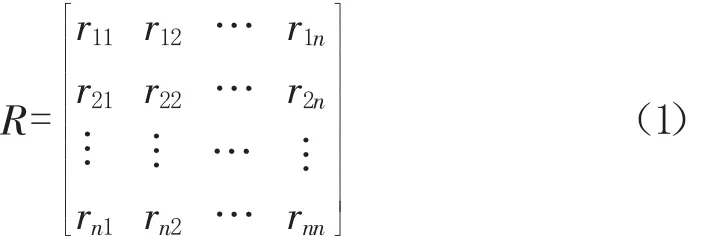
1.2.3把最优传递矩阵R转化为一致判断矩阵

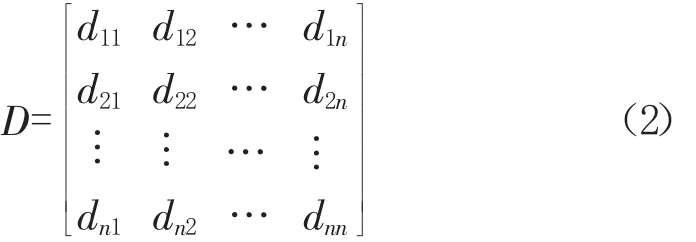
1.2.4评价指标权重计算

通过计算一致判断矩阵D的最大特征值及对应特征向量确定权重，即满足式DW=λmaxW的特征向量作为评价指标的权重，其中特征值向量采用方根法求解。

权重向量W=［w1w2… wn］计算公式为

2　AH P-TO PSI S评判模型的建立

在多目标决策分析中，逼近理想解排序法（TOPSIS）是一种常用的有效评价方法，又称优劣解距离法、理想解法、理想点法。TOPSIS法是通过有限个评价对象正负理想解的贴进度进行排序的方法［14，15］。

2.1构造初始判断矩阵

设评价对象集P=｛P1，P2，…，Pm｝，每个评价对象有n个评价指标X=｛X1，X2，…，Xn｝，相应的评价指标Xij表示第m个评价单元的第n个评价指标。其中，i=（1，2，…，m），j=（1，2，…，n），则构造的初始判断矩阵为

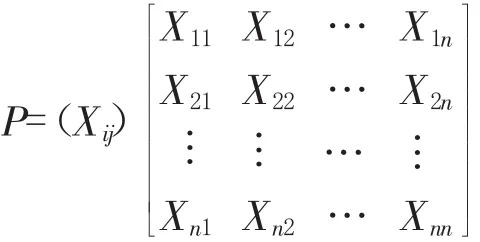
2.2建立规范化决策矩阵

考虑到评判对象中不同的评判指标具有不同的量纲和单位，为了消除由此产生的指标的不可公度性，对评判指标进行无量纲化处理（同趋势化）［12，14，15］，得到规范化决策矩阵B。其中，B=（bij）m×n的元素计算如下：

收益性指标，越大越优，即

2.3建立加权规范化决策矩阵

加权规范化决策矩阵通过规范化决策矩阵B的每列与改进的层次分析法所确定的权重wj相乘得到，即

2.4评价对象贴近度分析

2.4.1确定加权规范化决策矩阵C的正理想解C+和负理想解C

C+=｛maxci1，maxci2，…，maxcin｝=｛c1+，c2+，…，cn+｝

（其中，如果指标没有同趋势化，收益性指标取最大值，消耗性指标取最小值）

C-=｛minci1，minci2，…，mincin｝=｛c1-，c2-，…，cn-｝

（其中，如果指标没有同趋势化，收益性指标取最小值，消耗性指标取最大值）

2.4.2计算各评价对象与理想解的距离

评价对象到正理想解的距离

2.4.3计算各评价对象与正理想解的贴进度

贴近度fi+反映了评判对象靠近正理想解、远离负理想解的程度，fi+越大，评判对象越靠近正理想解。当评判对象为正理想解时，fi+=1；当评判对象为负理想解时，fi+=0。但一般评判对象贴近度都在0～1，故只考虑评判对象靠近正理想解的贴近度，通过贴近度值降序排列，可以对评判对象进行选择评判。

3　边坡稳定性评价实例应用

3.1边坡稳定性影响因素

影响边坡稳定性的指标很多，参考有关岩土边坡稳定性评价体系［10，11］，考虑主要影响因素，经综合分析后确定以岩石质量指标（X1）、岩体完整性指标（X2）、地应力（X3）、黏聚力（X4）、内摩擦角（X5）、坡高（X6）和日最大降水量（X7）7个指标作为影响边坡稳定性的因素。它们基本反映了地层岩性、地质构造、岩体结构、水文地质条件、地应力分布等性质，且这些指标比较容易获得。

3.2边坡稳定性等级分类标准

按照边坡稳定性影响因素的单指标分类区间将边坡稳定性程度划分为5个等级，分别为稳定Ⅰ级、较稳定Ⅱ级、基本稳定Ⅲ级、不稳定Ⅳ级和极不稳定Ⅴ级［6，10，11］。稳定性等级评价准则见表2。

表2　边坡稳定性分类准侧

3.3边坡稳定性评价指标权重确定

根据改进层次分析法的基本原理，查阅大量文献及工程资料，并与现场工作者、有关专家学者协商，构造的比较矩阵为

将比较矩阵A用式（1）转化为最优传递矩阵R，有

由式（2）将矩阵R转化为一致性判断矩阵D，有

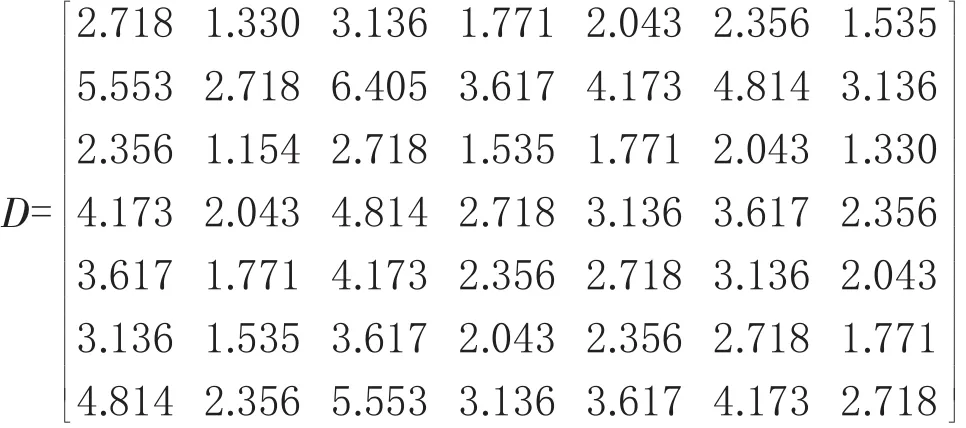
由式（3）计算各评价指标权重为

w1=0.262 4，w2=0.536 1，w3=0.227 5，w4=0.402 9，w5=0.349 3，w6=0.308 2，w7=0.464 7

分析可知，岩体完整性指标对边坡稳定性影响最大，其次是日最大降水量、黏聚力、内摩擦角、坡高及岩石质量指标，影响最小的是地应力。

3.4AHP-TOPSISI模型及实例应用

将改进的AH P-TOPSIS模型应用于文献［16］中公路边坡（S1）和文献［11］中矿区边坡（S2，S3，S4）稳定性评价。其中，S1、S2、S3、S4边坡稳定性指标的实测数据见表3。

根据表2中单指标分类区间下限构造的5个不同等级的临界值边坡Ⅰ0、Ⅱ0、Ⅲ0、Ⅳ0、Ⅴ0，与表3稳定性待评价边坡S1、S2、S3、S4的实测数据构造AH P-TOPSISI模型的初始评判矩阵P，其中前5行为临界值边坡数据，后4行为待预测边坡的评价指标数据。

表3　稳定性指标实测数据

对初始判断指标进行无量纲化处理，由表2可知指标X1、X2、X4、X5为收益性指标，越大越好，由式（4）处理；指标X3、X6、X7为消耗性指标，越小越好，由式（5）处理；得到规范化决策矩阵B。

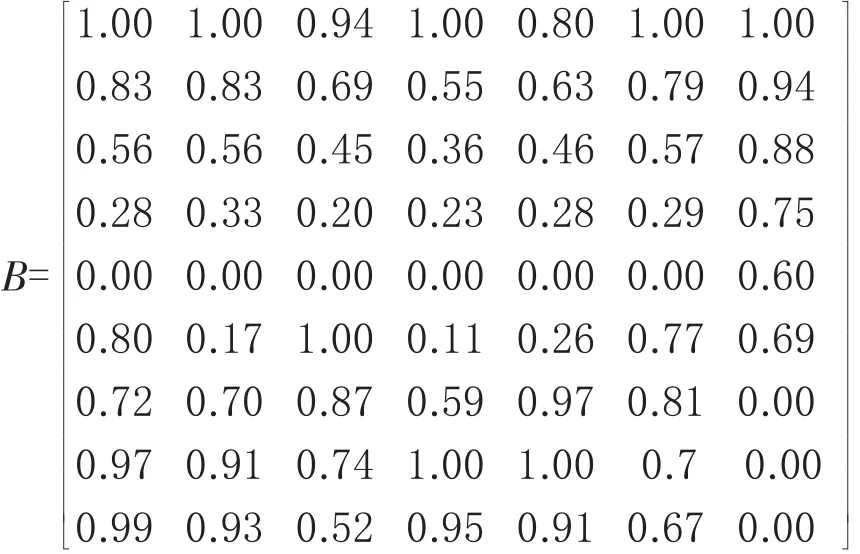
由式（6），计算得到加权规范化决策矩阵C。

由加权规范化矩阵C可得正理想解与负理想解

由式（7）～式（9）可得到临界值边坡稳定性及待评价边坡稳定性距正理想解的距离Di+，距负理想解的距离Di-，以及与正理想解的贴近度fi+，结果见表4。

表4　边坡稳定性评价结果

由表4可知，岩土边坡稳定性的贴近度分类区间为：

将边坡S1、S2、S3、S4稳定性贴进度与上述分类区间对比可知，S1为极不稳定Ⅴ级，S2为基本稳定Ⅲ级，S3为较稳定Ⅱ级，S4为较稳定Ⅱ级。其中S3用灰色关联法［6］和可拓评价法［11］评价结果为稳定性Ⅰ级，本文判别为较稳定Ⅱ级，但结果偏于安全，且该评价方法计算简单，同时能够对边坡稳定性程度进行排序。因此，改进的AH P-TOPSIS评价法用于岩土边坡稳定性评价是可行的。

4　结语

（1）采用改进的AH P法计算边坡稳定性各评价指标的权重，降低权重确定的主观性，避免了传统9标度层次分析法的一致性检验，减少计算量，提高了计算精度，从而提高评价的准确性。

（2）将改进的AH P法与多目标决策理论中的TOPSIS法结合用运到岩土边坡稳定性评价中，AH P法能够在一定程度上有效地克服TOPSIS法由于因素过多而难以分配权重的弊端，同样也避免了主观因素引起的决策失误，能做出更科学、全面、准确的判断。通过实例证明了改进模型对边坡稳定性评价的可行性与合理性，且该模型也可应用于其他多指标评价决策系统中。

［1］孙书伟，朱本珍，马惠民.一种基于模糊理论的区域性高边坡稳定性评价方法［J］.铁道学报，2010，32（3）:77-83.

［2］蔡美峰，何满潮，刘东燕.岩石力学与工程［M］.北京:科学出版社，2002:10-25.

［3］张菊连，沈明荣.高速公路边坡稳定性评价新方法［J］.岩土力学，2011，32（12）：3623-3629.

［4］李云，刘霁.基于模糊集理论与 CSM R的岩质边坡稳定性分析［J］.中南大学学报（自然科学版），2012，43（5）:1940-1946.

［5］张士伦，张孟喜，吉随旺，等.基于模糊分析的松散体边坡稳定性评价［J］.上海交通大学学报，2015，49（7）：1035-1039.

［6］丁丽宏.基于改进的灰关联分析和层次分析法的边坡稳定性研究［J］.岩土力学，2011，32（11）:3437-3441.

［7］赵建军，贺宇航，黄润秋，等.基于因子分析法的边坡稳定性评价指标权重［J］.西南交通大学学报，2015，50（2）：325-330.

［8］冯夏庭，王泳嘉，卢世宗.边坡稳定性的神经网络估计［J］.工程地质学报，1995，3（4）:54-61.

［9］黄志全，崔江利，刘汉东.边坡稳定性预测的混沌神经网络方法［J］.岩石力学与工程学报，2005，23（22）:3808-3812.

［10］王新民，康虔，秦健春，等.层次分析法-可拓学模型在岩质边坡稳定性安全评价中的应用［J］.中南大学学报（自然科学版），2013，44（6）:2456-2462.

［11］王润生，李存国，郭立稳.基于可拓理论的高陡边坡稳定性评价［J］.矿业安全与环保，2008，35（6）:25-28.

［12］徐玖平，吴巍.多属性决策的理论与方法［M］.北京:清华大学出版社，2006:28-30.

［13］吴仲雄，高清平.改进AH P法在采矿方法多目标决策中的应用［J］.矿业工程，2005，3（5）:18-20.

［14］胡建华，尚俊，龙雷涛.基于RS-TOPSIS法的地下工程岩体质量评价 ［J］.中南大学学报（自然科学版），2012，43（11）：4412-4419.

［15］龚剑，胡乃联，崔翔，等.基于AH P-TOPSIS评判模型的岩爆倾向性预测［J］.岩石力学与工程学报，2014，33（7）:1442-1448.

［16］李克钢，侯克鹏，李旺.指标动态权重对边坡稳定性的影响研究［J］.岩土力学，2009，30（2）:492-496.

TU457

A

1009-7716（2016）09-0211-05

2016-05-11

姜廷文（1988-），男，甘肃武威人，硕士（在读），土木工程建造与管理专业。