约束阻尼型镗杆的优化及减振性能

刘洋， 刘战强， 宋清华

山东大学　机械工程学院 高效洁净机械制造教育部重点实验室， 济南　250061



约束阻尼型镗杆的优化及减振性能

刘洋， 刘战强*， 宋清华

山东大学机械工程学院 高效洁净机械制造教育部重点实验室， 济南250061

孔加工过程中镗杆的切削颤振影响着表面加工质量和加工精度，约束阻尼型镗杆可有效抑制这种切削振动，但其作用机理未被完全研究清楚，导致其抑制振动的效果一般。对约束阻尼型镗杆的结构优化、材料优选及减振性能进行了理论和实验研究。首先，根据Kelvin-Voigt粘弹性力学模型理论建立了镗杆的动力学模型，研究证实增大镗杆的静刚度和结构损耗因子能提高其减振性能从而提高孔加工质量；其次，基于建立的约束阻尼型镗杆静刚度和结构损耗因子理论公式，对其进行结构优化、材料优选。结果显示：存在一个最佳尺寸范围可减小镗杆在主要工作频域段上的振动，同时所选用的阻尼层应具有较小的弹性模量和较大的材料损耗因子，约束层材料应具有较大的弹性模量；最后，设计制造4种不同材料的约束阻尼型镗杆，通过模态实验获得静刚度、结构损耗因子，并与理论计算结果进行对比分析，同时研究切削过程中约束阻尼型镗杆的材料及切削参数对减振性能的影响。结果显示：约束阻尼型镗杆能有效减小径向振动以提高加工质量，不同材料的约束阻尼型镗杆在切削过程中径向振动差别较大，优化后的钢-PMMA-硬质合金镗杆在不同切深及转速下的径向振动加速度较小且更加稳定。

约束阻尼； 损耗因子； 结构优化； 模态实验； 切削稳定性

在深孔镗削过程中，由于镗杆悬伸过长导致刚性相对减小，不稳定的切削过程导致工件表面产生振痕、加快刀具磨损与破损及产生过大的噪声等问题[1]，从而降低了加工质量和加工精度。对于深孔加工的振动抑制问题，国内外的研究人员在高性能减振镗杆的设计开发上，已开展了相关研究工作，采用的方法从振动控制角度可分为主动控制和被动控制[2]。

主动控制将反馈控制原理应用于频率低的大型镗杆，Akesson等[3]设计开发了压电驱动自适应控制的抑振镗杆；刘鹏[4]利用压电陶瓷的正负压电效应，将感知压电片得到的电信号反向放大后加到执行压电片上，产生反向振动来抑制切削颤振。

被动控制通过动力结构、冲击结构以及阻尼结构等将振动能转换为热能等其他形式的能量来达到减振效果，如Hahn[5]把高密度质量块置放在刀具空腔里，并在空腔内注入重油来提高镗杆动刚度，此方法已用来设计大长径比减振刀杆；Ema和Marui[6]利用质量块加间隙结构设计出冲击阻尼器并安装在镗杆后刀面上，有效减小了镗杆径向振动；Hwang和Kim[7]利用高刚度碳纤维环氧复合材料制成阻尼结构镗杆，在大悬伸条件下应用未发生明显的颤振。其中阻尼结构由于具有振动损耗能力强及结构简单的特点，目前已广泛应用于工程实际中，尤其是航空领域[8]。

综上分析发现：减振镗杆当前的研究重点是通过提高镗杆的刚度或阻尼性能达到减振效果[9-11]，很少将两者结合起来分析研究。事实上，要提高镗削稳定性及镗孔加工精度，必须综合提高镗杆的静刚度和阻尼性能，尤其对于高速镗孔或难加工材料的镗削加工。对约束阻尼型镗杆进行结构优化和材料优选，能够解决增大镗杆阻尼性能的同时造成刚度损失的问题，全面提高镗杆的刚度和阻尼性能，获得高减振性能和高切削稳定性的减振镗杆。

1　约束阻尼型镗杆的结构及动力学模型

阻尼结构主要分为两种形式：自由阻尼结构和约束阻尼结构[12]，如图1所示。自由阻尼结构由基体和阻尼层组成，通过胶粘或其他方式将基体和阻尼层结合；约束阻尼结构中，阻尼层置于两层弹性材料之间，即基体和约束层之间。自由阻尼结构更加依赖阻尼层厚度来发挥其减振效果，而约束阻尼结构使用较薄的阻尼层就可获得较高的结构损耗因子，与自由阻尼结构相比，可耗散更多的振动能量，减振效果更好[13-14]。

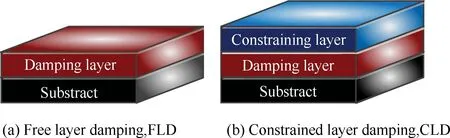
图1　两种典型阻尼结构Fig.1　Two representative damping structures

约束阻尼型镗杆的外形尺寸与普通镗杆一致，其结构主要由3部分组成：基体(包括切削头)、阻尼层和约束层，约束阻尼型镗杆在切削过程中，切削头处产生振动能量传递到基体中，振动产生弯曲带动阻尼层拉伸，而约束层的伸长远小于阻尼层的伸长，从而阻止阻尼层的伸长；当阻尼层压缩时，约束层又阻止阻尼层的压缩，由于阻尼层的拉伸和压缩受到约束层的阻碍，因而阻尼层承受拉伸和压缩交变载荷，振动能量在阻尼层被大量耗散，由此可实现抑制切削颤振、提高切削过程稳定性的目的[15-16]。本文以如图2所示的约束阻尼型镗杆结构为例进行分析，镗杆长度L=250 mm，直径D3=32 mm，基体直径为D1，阻尼层外圆直径为D2，约束层中面处的直径为D13。

图2　约束阻尼型镗杆的结构Fig.2　Structure of constrained damping boring bar

镗杆在切削加工过程中，自由端受到3个作用力，其中轴向力较小且作用于镗杆轴线上，对镗杆径向位移影响很小，切向力产生的扭矩对镗杆径向位移影响也较小，而径向力对镗杆末端(刀尖处)的径向位移影响较大[17]，所以理论计算时只考虑径向力的影响，加工过程中受到的径向周期性激振力为

F(t)=F0eiω t

(1)

式中：F0为径向激振力的最大幅值；ω为径向激振力的频率；t为时间。

假设镗杆与刀架的定位连接为刚性装夹，镗杆杆体可视为一端固定、一端自由的悬臂结构，由于阻尼层和约束层是连续的，故根据Kelvin-Voigt粘弹性力学模型[18]，在任意方向上将阻尼层和约束层简化为n个弹簧-阻尼元，kri-cri和kti-cti(i=1,2,…,n)表示镗杆径向和切向上弹簧-阻尼元的静刚度和阻尼系数，从而将该振动系统简化为杆体-弹簧-阻尼系统[19]，如图3所示，x(t)为径向位移。

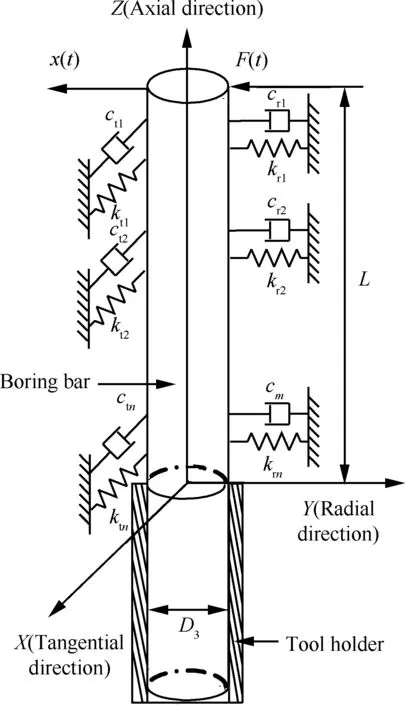
图3　约束阻尼型镗杆的动力学模型Fig.3　Dynamic model of constrained damping boring bar

根据Kelvin-Voigt粘弹性力学模型，约束阻尼型镗杆的静刚度和阻尼系数为

(2)

式中：k为镗杆的静刚度；c为阻尼系数。

根据式(2)将该振动系统建模为一个有阻尼的单自由度质量-弹簧-阻尼受迫振动系统，刀头端位移和激振力满足：

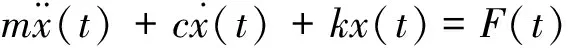
(3)

式中：m为镗杆的质量。

根据振动力学理论，镗杆的阻尼系数c可表示为

(4)

式中：η为镗杆的结构损耗因子。

将式(1)和式(4)代入非齐次方程式(3)，求解获得在径向周期性激振力下产生的径向持续等幅振动为

(5)

式中：s=ω/ω0，ω0为镗杆的固有频率；θ为相位角。可见，增大镗杆的静刚度k和结构损耗因子η有利于减小振动。

2　静刚度和结构损耗因子

利用式(2)求解静刚度和阻尼系数的计算量较大，计算精度不能保证，且不能得到镗杆的结构损耗因子。本文利用材料力学、振动力学理论，结合约束阻尼结构的特点，求解镗杆整体结构的静刚度和结构损耗因子，首先做出如下假设：①基体、阻尼层和约束层的弯曲变形在各个方向上是一致的；②基体-阻尼层、阻尼层-约束层的接触面无相对滑动；③阻尼层材料均匀(有固定厚度)且各向同性；④只考虑径向力的影响。

根据材料力学理论，约束阻尼型镗杆的静刚度与材料的弯曲刚度成正比，即与材料的弹性模量及镗杆的截面形状有关[20]，可表示为

(6)

式中：(EI)w为镗杆悬伸段的当量弯曲刚度；E为材料弹性模量；I为横截面对弯曲中性轴的惯性矩。

约束阻尼结构的当量弯曲刚度可用基体、阻尼层与约束层材料弯曲刚度直接代数相加的方法计算，可表示为

(EI)w=(EI)1+(EI)2+(EI)3

(7)

式中：(EI)1、(EI)2和(EI)3分别为基体、阻尼层和约束层的弯曲刚度。将式(7)代入式(6)可得约束阻尼型镗杆的静刚度为

(8)

式中：E1、E2和E3分别为基体、阻尼层和约束层材料的弹性模量。

镗杆发生弯曲时，基体和约束层截面受弯矩和剪力作用，截面上既有正应力又有剪应力，对于金属弹性层，可忽略剪切应变的影响，只计算弯曲耗能[21]，与弯曲耗能有关的基体、约束层的刚度参数Y为

(9)

式中：B1、B3分别为基体、约束层绕各自中性轴的弯曲刚度，可表示为

(10)

与自由阻尼结构阻尼层的弯曲耗能不同，约束阻尼结构阻尼层内主要靠产生剪切应变和剪切应力来消耗振动能量，忽略弯曲耗能，与剪切耗能有关的阻尼层的剪切参数X为

(11)

式中：G2为阻尼层材料的剪切模量；P2为阻尼层的阵型波数，根据振动力学理论，其表达式为

(12)

文献[22]针对约束阻尼梁结构提出剪切阻尼理论，约束阻尼型镗杆的结构损耗因子为

(13)

式中：β为阻尼层的材料损耗因子。将式(9)～式(12)代入式(13)可求出约束阻尼型镗杆的结构损耗因子。

可见，影响约束阻尼型镗杆静刚度和结构损耗因子的因素包括两类：① 与结构尺寸有关的基体、阻尼层的直径D1、D2及镗杆的悬伸长度L。② 与材料力学性能参数有关的基体、阻尼层及约束层材料的密度、弹性模量及材料损耗因子，因此分别对约束阻尼型镗杆进行结构优化和材料优选。

3　约束阻尼型镗杆的结构优化

为分析基体、阻尼层的直径D1、D2对约束阻尼型镗杆静刚度和结构损耗因子的影响，设定镗杆的悬伸长度L=160 mm，悬伸比为5∶1(普通镗杆切削加工容易出现振动的悬伸比[23])，利用MATLAB对静刚度和结构损耗因子理论公式进行分析，结果如图4所示。

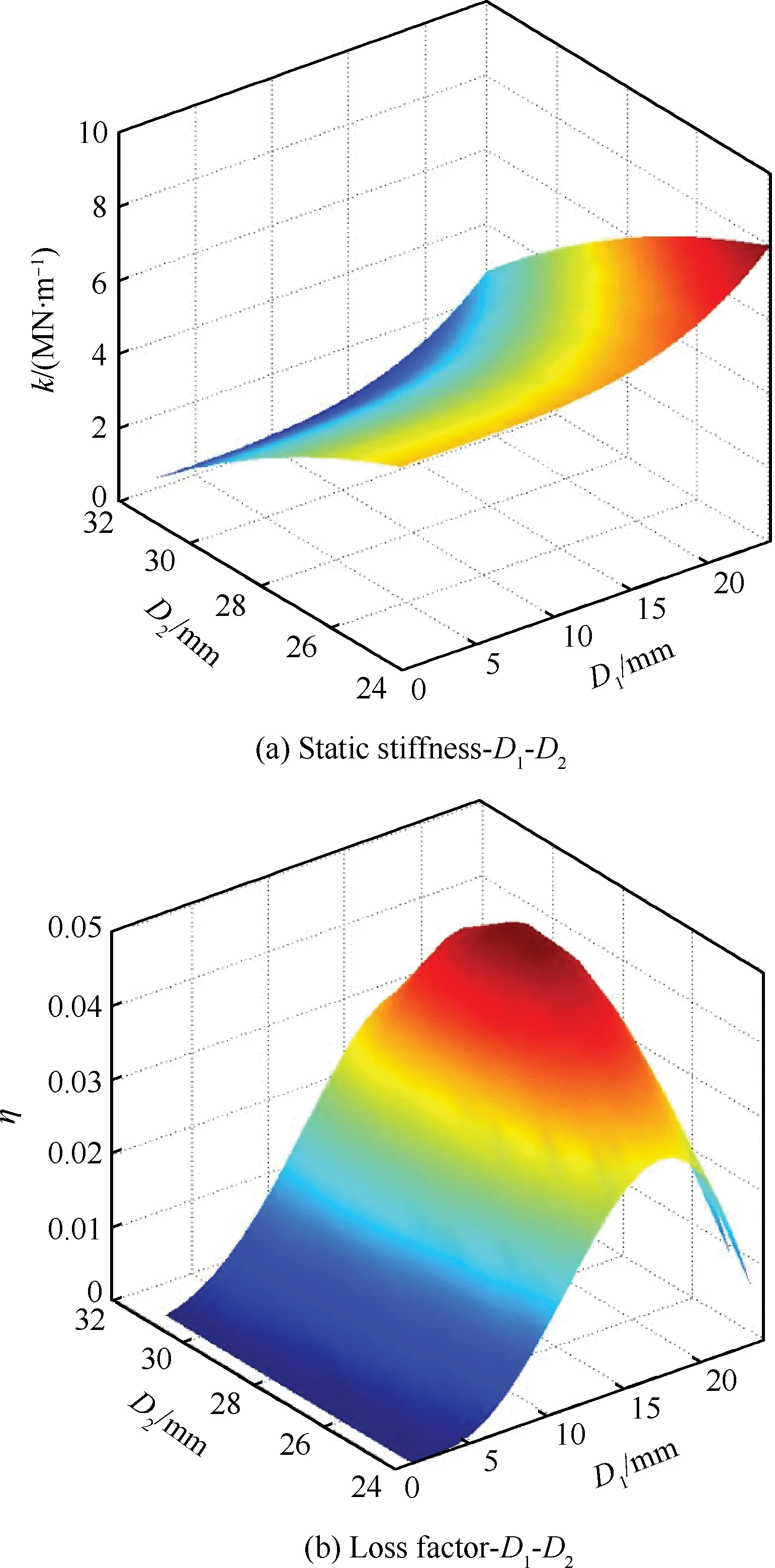
图4　结构尺寸与静刚度/损耗因子的关系Fig.4　Relationship between structure sizes and static stiffness/loss factor

约束阻尼型镗杆的静刚度随着基体直径D1的增大和阻尼层直径D2的减小(即阻尼层厚度减小)而增大；结构损耗因子随阻尼层直径D2增大而增大，随着基体直径D1增大呈现先增大后减小的趋势。

由图4还可见，无法同时最大化静刚度和结构损耗因子以取得最佳减振效果。kmax和ηmax分别表示静刚度和结构损耗因子最大时对应的结构尺寸，ηkopt表示利用图4两曲面相交拟合得到的结构尺寸，如表1所示。

为分析3组结构优化尺寸对应的约束阻尼型镗杆刀头端的振动情况，由式(4)可得

(14)

式中：β(s)为刀头端振幅的放大因子。计算得到不同结构优化尺寸的约束阻尼型镗杆幅频特性如图5所示。

表1约束阻尼型镗杆结构优化尺寸

Table 1Structure optimized sizes of constrained damping boring bar

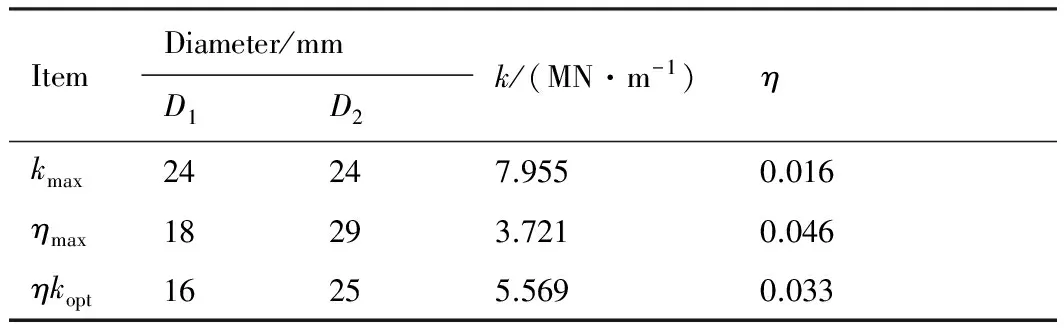
ItemDiameter/mmD1D2k/(MN·m-1)ηkmax24247．9550．016ηmax18293．7210．046ηkopt16255．5690．033

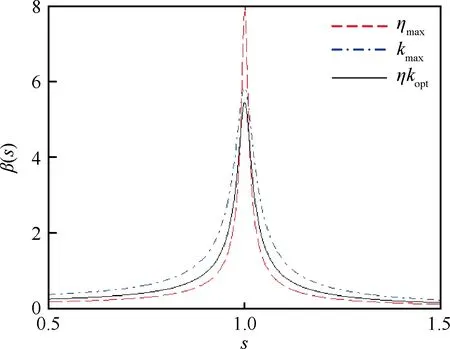
图5　不同结构优化尺寸的镗杆幅频特性Fig.5　Amplitude-frequency characteristics between boring bars with different structure optimized sizes

在远离共振频率(s=1)处，利用ηmax对应的结构尺寸设计有利于减小镗杆振动，但在共振频率附近，振幅急剧增大，振动损耗能力在共振时较弱。ηkopt对应结构尺寸的镗杆在远离共振频率处，振幅介于kmax和ηmax之间，共振振幅相比于kmax和ηmax分别减小了6.8%和30.7%，振动损耗能力在共振时优于ηmax，而在整个频域段上都优于kmax。

从结构优化结果可见：ηkopt对应的结构优化尺寸的约束阻尼型镗杆的共振振幅及在主要工作频域段上的振动较小，振动损耗能力强。

4　阻尼层、约束层材料优选

由约束阻尼型镗杆的静刚度理论式(8)知，镗杆的静刚度只与基体、阻尼层及约束层材料的弹性模量有关。基体选用镗杆常用材料普通合金钢，分析得到阻尼层、约束层材料的弹性模量与静刚度的关系如图6(a)所示。通过拟合得到阻尼层、约束层材料弹性模量的平均影响因子之比约为1∶1.99，选择弹性模量大的约束层材料将有效增大镗杆的静刚度。

由结构损耗因子理论式(13)知，除了弹性模量外，结构损耗因子还与密度及材料损耗因子有关。由于密度的影响较小，故不予考虑。分析得到阻尼层、约束层材料的弹性模量与结构损耗因子的关系如图6(b)所示。可见当阻尼层材料的弹性模量增大到一定程度时，结构损耗因子几乎为零，阻尼层材料的弹性模量应控制在10 GPa以下，并增大约束层材料的弹性模量。

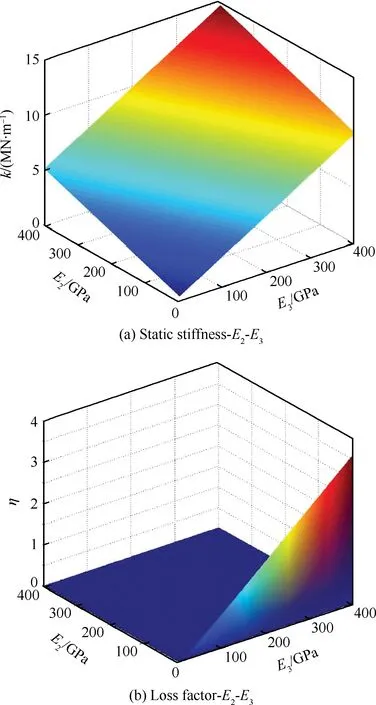
图6　弹性模量与静刚度/损耗因子的关系Fig.6　Ralationship between elastic modulus and static stiffness/loss factor

阻尼层一般选择粘弹性材料，这是因为粘弹性材料在一定受力状态下，既具有粘性液体消耗能量的特性，又具有弹性固体材料存贮能量的特性，当产生动态应力或应变时，有一部分能量被转化为热能而耗散掉，而另一部分能量以势能的形式储存起来，从而将振动机械能转变为热能，特别适合作为约束阻尼结构的阻尼层。粘弹性阻尼层的材料损耗因子可表示为

(15)

式中：Ed为阻尼层材料的损耗模量，与损耗能量有关；Es为阻尼层材料的储存模量，即弹性模量，与储存能量有关。

镗杆的结构损耗因子与阻尼层材料弹性模量、损耗模量及材料损耗因子的关系如图7所示。

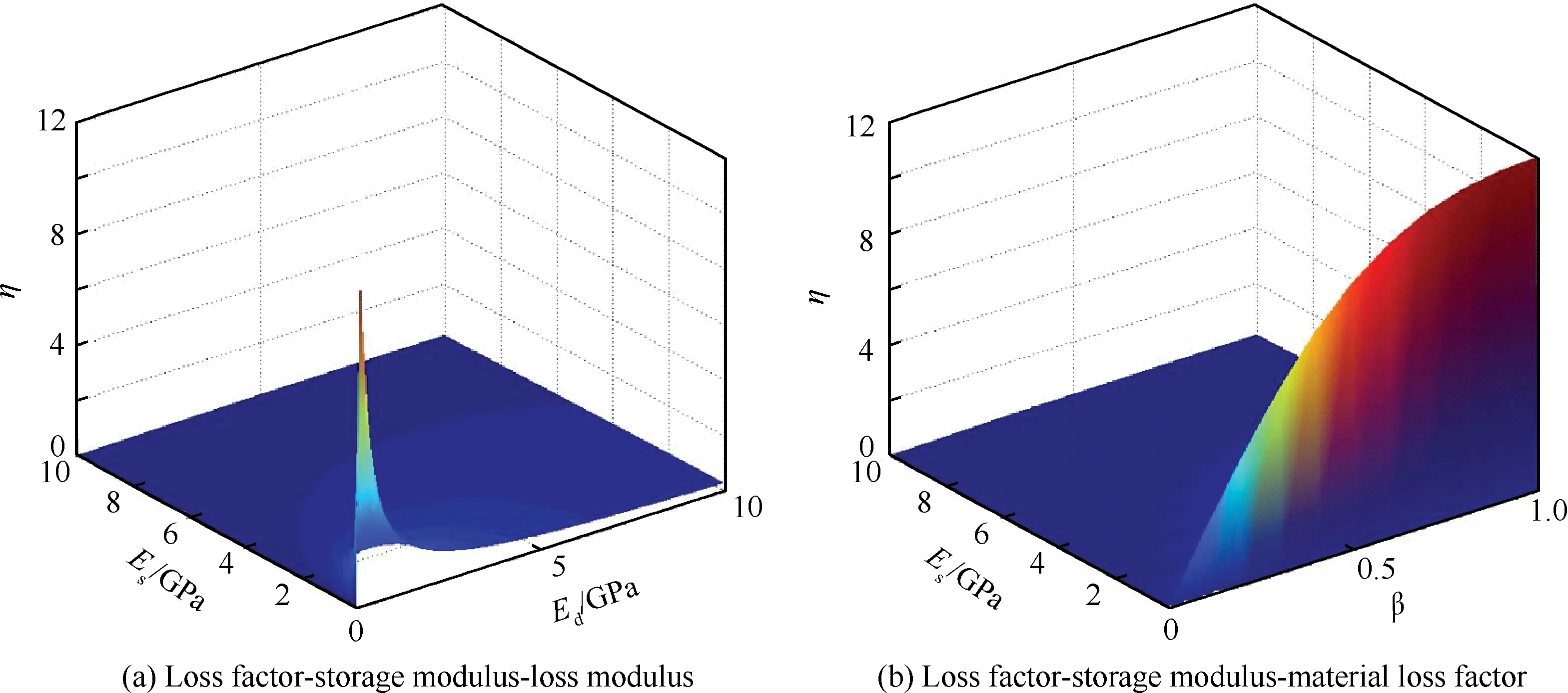
图7　阻尼层材料参数与结构损耗因子的关系Fig.7　Ralationship between damping material parameters and structure loss factor

在阻尼层的材料参数中，结构损耗因子受材料损耗因子的影响最大，应当选取材料损耗因子大的高阻尼粘弹性阻尼材料。

经过材料优选：①利用粘弹性阻尼材料自身的特性(材料损耗因子大、弹性模量小)极大地增强了镗杆的阻尼性能；②利用高弹性模量的约束层增大了镗杆的静刚度，使镗杆可以承受更大的切削力，一定程度上也增强了阻尼性能。

5　模态及切削稳定性测试

5.1模态实验

根据结构优化尺寸(基体直径D1=16 mm，阻尼层直径D2=25 mm)，设计制造了4种相同结构的约束阻尼型镗杆，其阻尼层和约束层材料不同，并与普通钢杆进行对比。约束层分别选择普通合金钢和硬质合金，阻尼层分别选择2种不同的粘弹性材料，环氧树脂和聚甲基丙烯酸甲酯(PMMA)[24-25]。不同材料镗杆对比如表2所示，所用材料的力学性能参数如表3所示。

将镗杆安装于机床主轴上，设置镗杆悬伸长度L=160 mm并夹紧，利用力锤冲击法测量镗杆的振动，加速度传感器型号为Dytran Type 3035B，灵敏度为100 mV/g，最大采样频率为10 kHz，对镗杆的振动及动态信号进行采集分析得到100～1 600 Hz区间的频率响应曲线，如图8所示，ln(a/F)为实验测得振动加速度与径向激振力的自然对数比。可见，钢-环氧树脂-钢镗杆的共振频率及整个频域范围内的振幅与普通钢杆相差不大；钢-PMMA-硬质合金镗杆的共振频率增大，振幅最小。

表2不同阻尼层/约束层材料镗杆对比

Table 2Comparison of boring bars with different damping/constraining layer materials

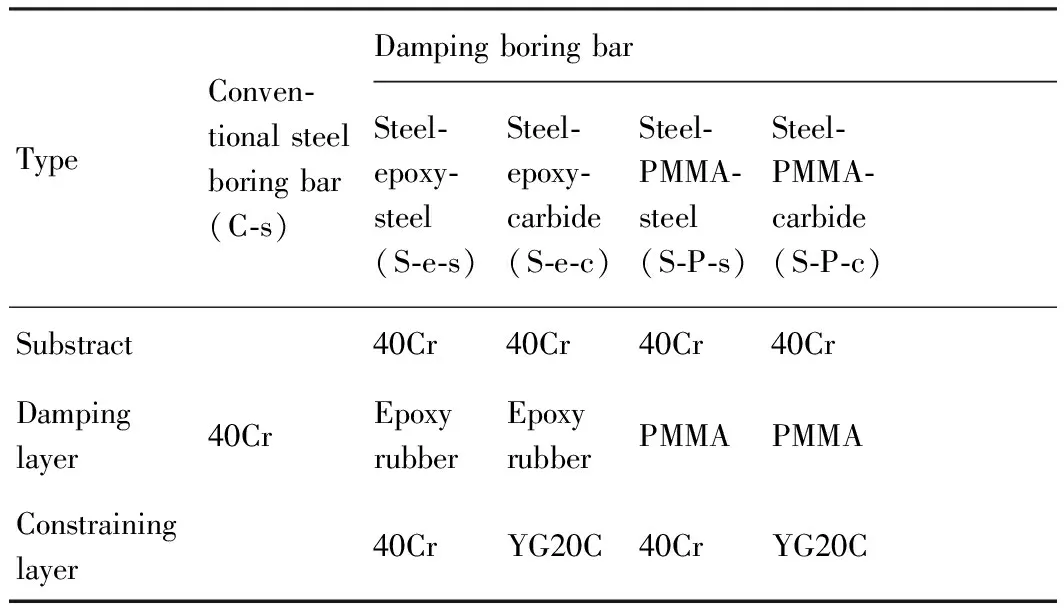
TypeConven⁃tionalsteelboringbar(C⁃s)DampingboringbarSteel⁃epoxy⁃steel(S⁃e⁃s)Steel⁃epoxy⁃carbide(S⁃e⁃c)Steel⁃PMMA⁃steel(S⁃P⁃s)Steel⁃PMMA⁃carbide(S⁃P⁃c)Substract40Cr40Cr40Cr40CrDampinglayer40CrEpoxyrubberEpoxyrubberPMMAPMMAConstraininglayer40CrYG20C40CrYG20C

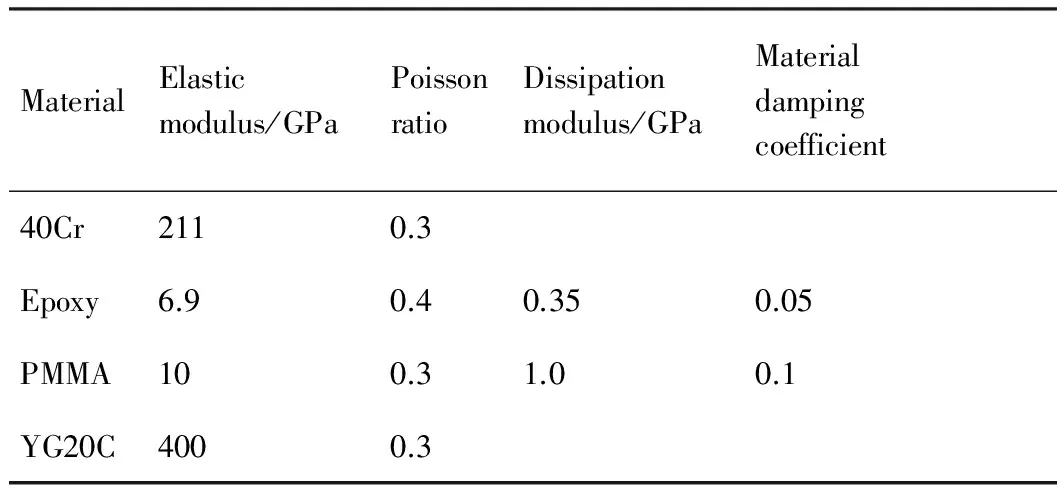
表3　镗杆材料力学性能参数

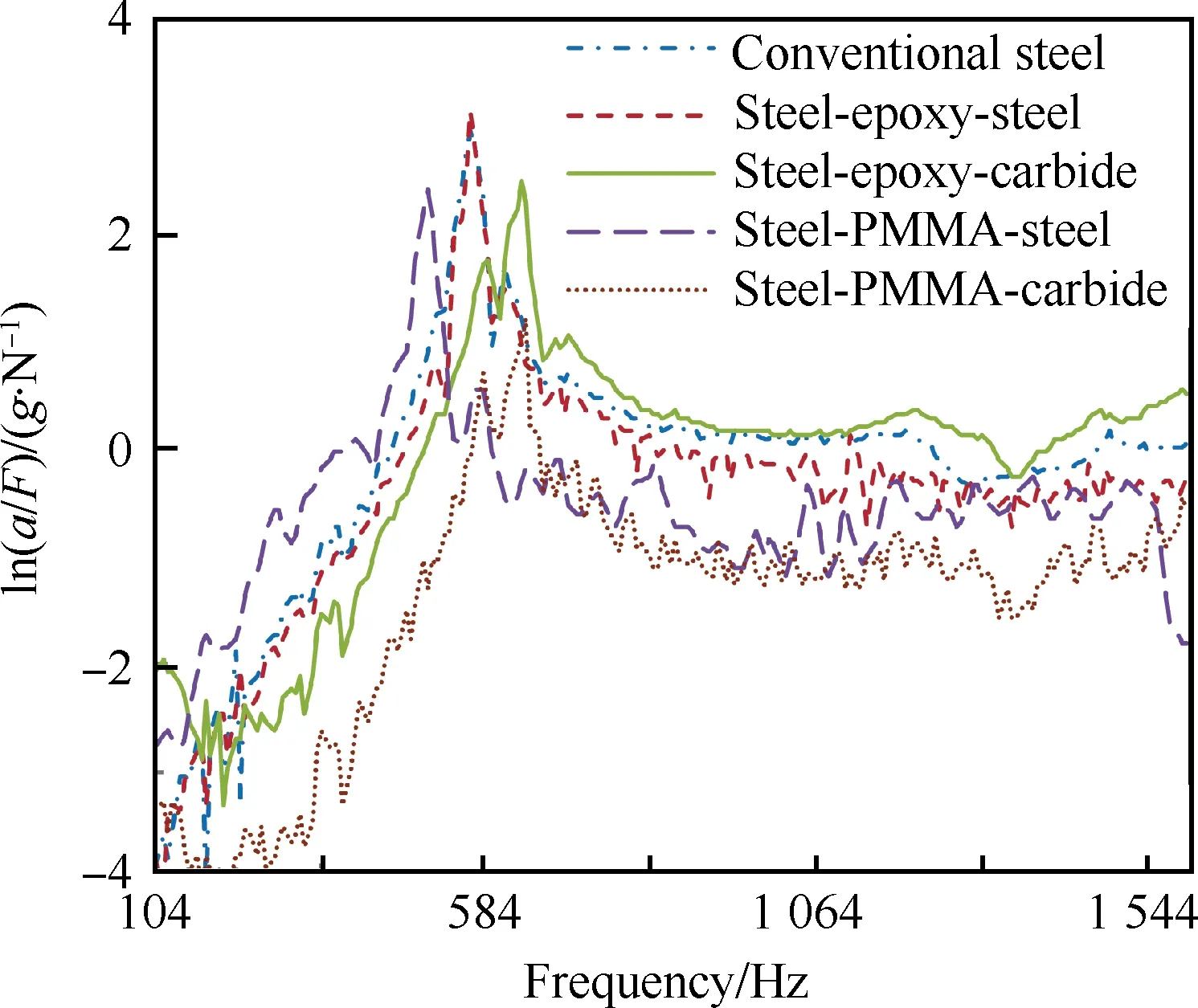
图8　不同阻尼层/约束层材料镗杆的频率响应曲线Fig.8　Frequency response curves of boring bars with different damping/constraining layer materials

提取模态参数，计算出镗杆的静刚度和结构损耗因子，分别为

(16)

实验结果和理论计算结果如图9所示，两者误差较小，验证了理论公式的准确性。钢约束层镗杆的静刚度比普通钢杆减小了约40%，这是由于粘弹性阻尼层材料的弹性模量小导致静刚度的损失；硬质合金约束层材料的弹性模量大，使静刚度得到了补偿。

钢-环氧树脂-钢和钢-PMMA-钢镗杆的结构损耗因子比普通钢杆分别增大了60%和100%，说明粘弹性阻尼层增大了结构损耗因子；硬质合金约束层镗杆的结构损耗因子最大，说明合理选择约束层材料能有效增大结构损耗因子。

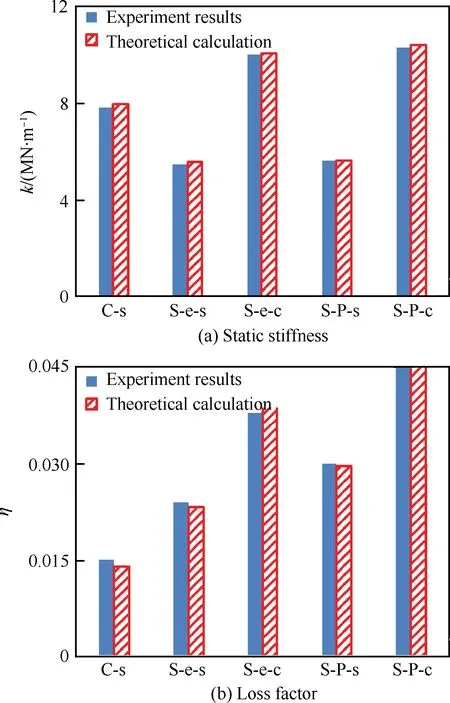
图9　不同材料镗杆的静刚度/损耗因子Fig.9　Static stiffness/loss factor of boring bars with different materials

5.2切削稳定性实验

通过对比镗杆在切削过程中的振动加速度及加工后的表面质量，验证镗杆的减振效果。在镗杆上离切削刃60 mm处安装2个单向加速度传感器，分别测量切削过程中的切向及径向振动加速度信号，传感器分布位置如图10所示。

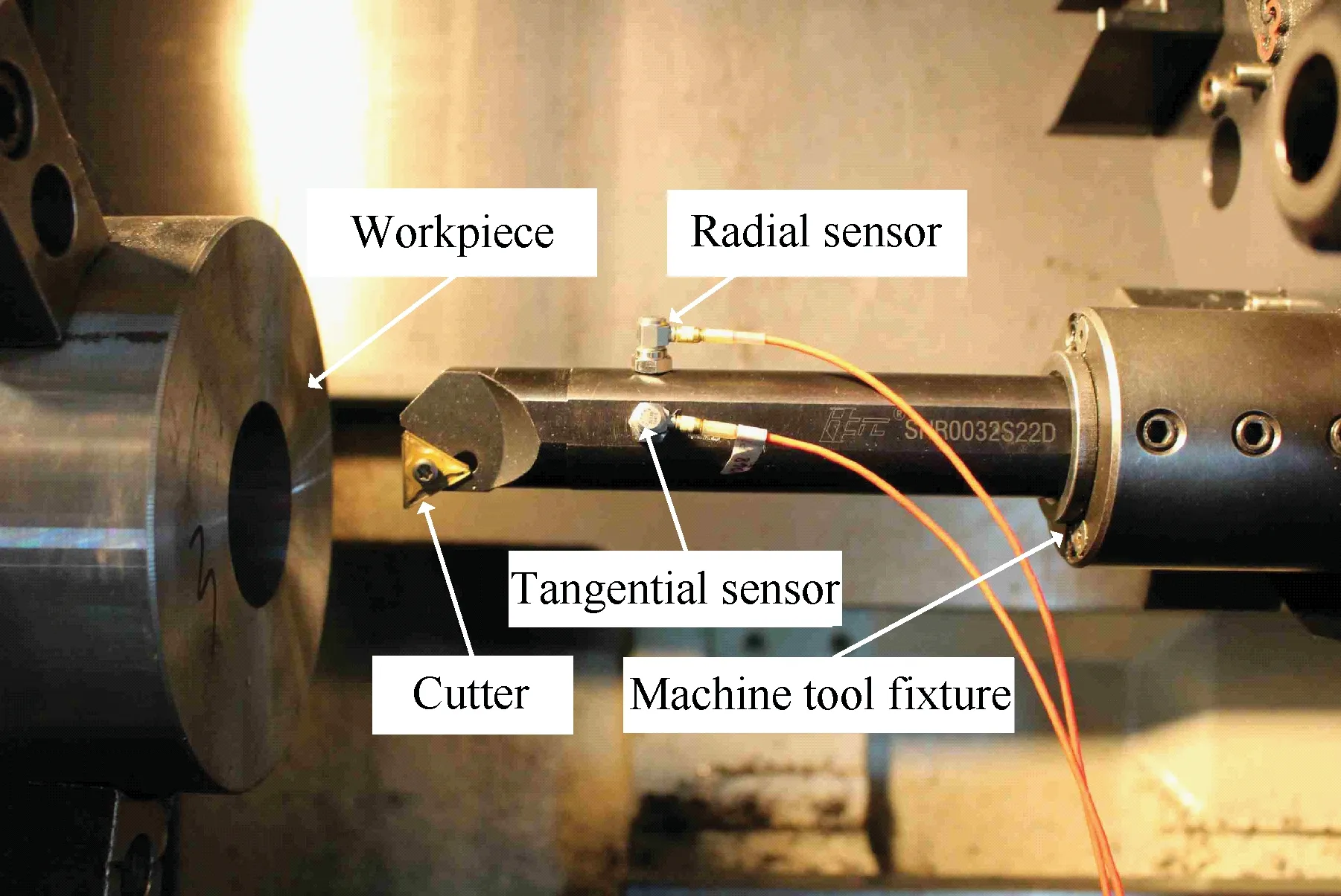
图10　镗杆切削振动加速度测试Fig.10　Cutting vibration acceleration test of boring bars

刀具为TNMG220408内圆车刀片，材料为硬质合金。工件材料为45号钢，工件直径为150 mm，厚度为100 mm，长度为50 mm。镗杆的悬伸长度与模态实验一致。为研究减振效果与镗杆材料及加工条件的关系，采取单一变量法，分别改变主轴转速和切深进行实验，实验条件如表4 所示。

表4　切削实验条件

以转速S=250 r/min，切深ap=0.1 mm为例，图11为实验测得普通钢杆和钢-环氧树脂-硬质合金镗杆在切削过程中的切向及径向振动加速度实时信号，其他实验条件及阻尼镗杆的实验结果此处未给出，但都符合此规律，可见钢-环氧树脂-硬质合金镗杆的切向振动加速度与普通钢杆差别不大，径向振动加速度大大减小，且变化幅度较小，切削过程更加稳定。

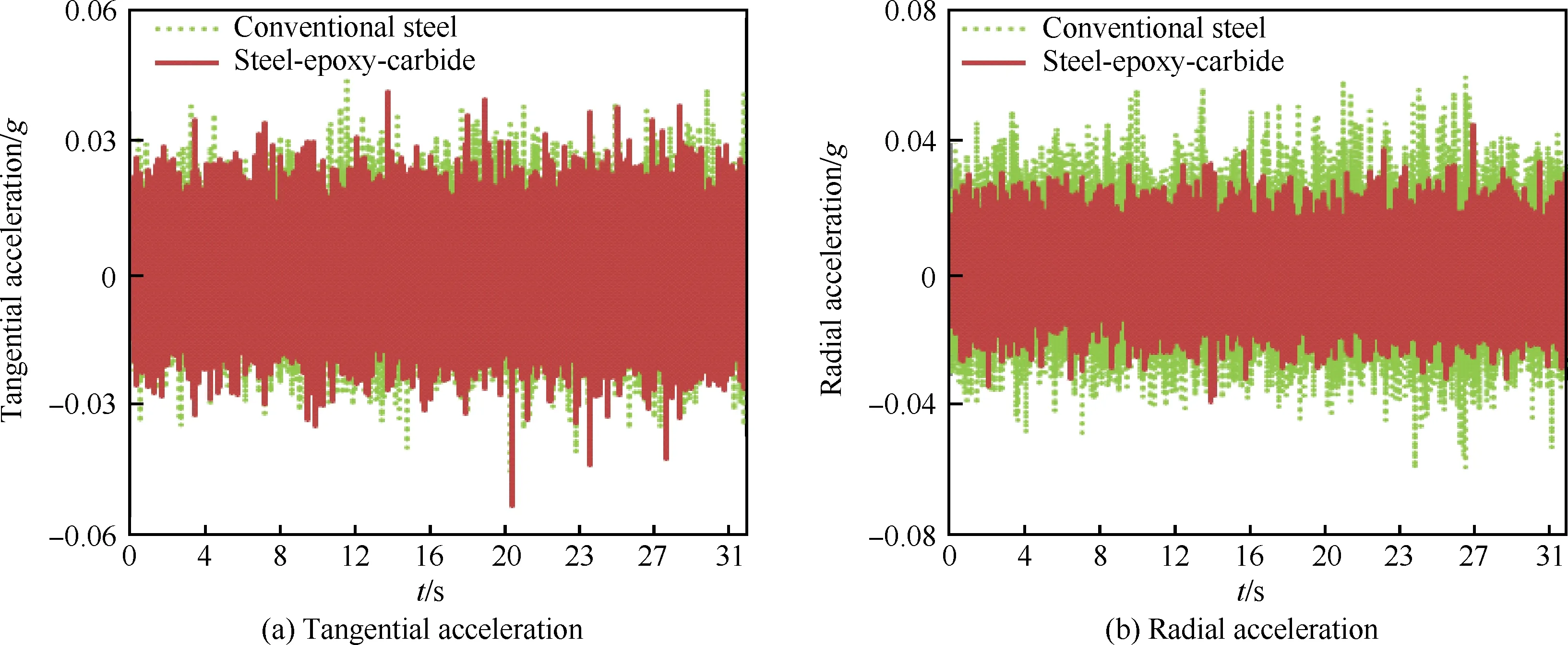
图11　切削过程中切向/径向振动加速度对比Fig.11　Comparison of tangential vibration acceleration to radial acceleration in cutting process

通过计算得到振动加速度实效值(简称RMS值)与加工后工件表面粗糙度进行对比，如表5所示，可见影响加工后表面质量的主要因素是径向振动。证明在切削过程中，约束阻尼型镗杆并不能明显抑制切向振动，但能够有效抑制径向振动，由此提高加工质量。

由于镗杆的减振性能主要体现在减小径向振动，当转速改变时，可忽略切向振动，计算得到径向RMS值，如图12(a)所示：①随着转速的增大，由于固有频率不同，镗杆径向振动的变化规律各不相同；②在0.5 mm的切深下，钢-环氧树脂-钢镗杆径向振动较大，不能实现减振效果，钢-PMMA-钢镗杆的径向振动在多数转速下都低于普通钢杆，径向RMS值平均降低了29.6%；③硬质合金阻尼层镗杆的径向RMS值平均降低了40%。

表5切向/径向加速度RMS值与表面粗糙度对比

Table 5Comparison of tangential/radial acceleration RMS and surface roughness

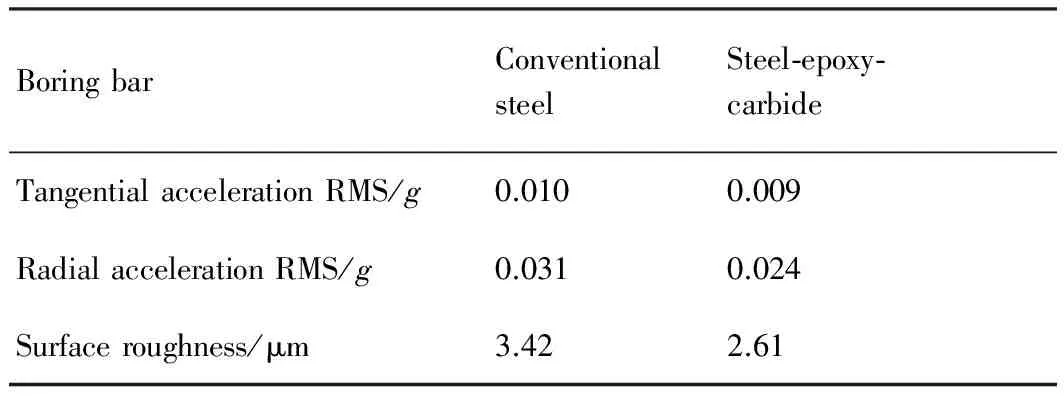
BoringbarConventionalsteelSteel⁃epoxy⁃carbideTangentialaccelerationRMS/g0．0100．009RadialaccelerationRMS/g0．0310．024Surfaceroughness/μm3．422．61

图12　切削参数与径向加速度RMS值的关系Fig.12　Ralationship between cutting parameters and radial acceleration RMS

当切深改变时，如图12(b)所示：①随着切深增大，镗杆的径向振动逐渐增大；②钢-环氧树脂-钢镗杆在切深小于0.4 mm时，可以实现一定的减振效果，径向RMS值平均降低了15.8%；③其他3种阻尼镗杆的径向振动明显低于普通钢杆，径向RMS值平均降低了70%。

6　结　论

1) 推导了约束阻尼型镗杆的静刚度和结构损耗因子理论公式，并对其进行结构优化、材料优选，结果显示，存在一个最佳尺寸范围可减小镗杆在主要工作频域段上的振动，对于本文所研究的镗杆，基体、阻尼层外径应分别取16、25 mm，所选用的阻尼层材料应具有较小的弹性模量和较大的材料损耗因子，约束层材料应具有较大的弹性模量。

2) 经过优化后设计制造的钢-PMMA-硬质合金镗杆的结构损耗因子比普通钢杆增加了294.4%，静刚度增加了32%，即在提高阻尼性能的同时补偿了静刚度，使镗杆的减振性能得到全面提升。

3) 通过研究切削过程中约束阻尼型镗杆的减振性能，结果发现约束阻尼型镗杆对切向振动影响不大，但能有效减小径向振动以提高加工质量。

4) 不同材料的约束阻尼型镗杆在切削过程中径向振动差别较大，其中经过结构优化和材料优选后的钢-PMMA-硬质合金镗杆的径向RMS值降低了约80%，减振性能及切削稳定性都有不同程度的提高。

[1]刘立佳, 刘献礼, 许成阳. 减振镗杆振动控制研究综述[J]. 哈尔滨理工大学学报, 2014, 19(2): 12-18.

LIU L J, LIU X L, XU C Y. Vibration control review of damping boring bar[J]. Journal of Harbin University of Science and Technology, 2014, 19(2): 12-18 (in Chinese).

[2]王珉, 区炳显， 昝涛， 等. 镗杆颤振控制技术发展综述[J]. 北京工业大学学报, 2011, 37(8): 1143-1147.

WANG M, OU B X， ZAN T， et al. Summary of boring bar chatter control technology[J]. Journal of Beijing University of Technology, 2011, 37(8): 1143-1147 (in Chinese).

[3]AKESSON H, SMIMOVA T, CLAESSON I. On the development of a simple and robust active control system for boring bar vibration in industry[J]. International Journal of Acoustics and Vibration, 2007, 12(4): 139-152.

[4]刘鹏. 压电智能镗杆振动主动控制的理论与实验研究[D]. 长春: 吉林大学, 2006: 22-35.

LIU P. Theoretical and experimental study of active vibration control of intelligent piezoelectric boring bar[D]. Changchun: Jilin University, 2006: 22-35 (in Chinese).

[5]HAHN R S. Design of Lanchester damper for elimination of metal-cutting chatter[J]. Transctions of ASME, 1951, 73(3): 201-213.

[6]EMA S, MARUI E. Suppression of chatter vibration of boring tools using impact dampers[J]. International Journal of Machine Tools and Manufacture, 2000, 40(8): 1141-1156.

[7]HWANG H Y, KIM J K. Design and manufacture of a carbon fiber epoxy rotating boring bar[J]. Composite Structures, 2003, 60(1): 115-124.

[8]SOOVERE J, DRAKE M L. Aerospace structures technology damping design guide. Volume 1. Technology review[R]. Burbank：Lockheed-California Co Burbank, 1985.

[9]秦柏. 阻尼动力减振镗杆动态特性仿真与优化设计研究[D]. 哈尔滨: 哈尔滨理工大学, 2009: 14-25.

QIN B. Dynamic characteristics analysis and optimization design of damping boring bar[D]. Harbin: Harbin University of Science and Technology, 2009: 14-25 (in Chinese).

[10]杨加明, 张义长, 吴丽娟. 多层黏弹性复合材料结构阻尼性能优化设计[J]. 航空学报, 2011, 32(2): 265-270.

YANG J M, ZHANG Y C, WU L J. Multilayered viscoelastic damping properties of composite structural optimization design[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(2): 265-270 (in Chinese).

[11]RUBIO L, LOYA J A, MIGUELEZ M H. Optimization of passive vibration absorbers to reduce chatter in boring[J]. Mechanical Systems and Signal Processing, 2013, 41(1): 691-704.

[12]ZHANG S H, CHEN H L. A study on the damping characteristics of laminated composites with integral viscoelastic layers[J]. Composite Structures, 2006, 74(1): 63-69.

[13]QI L F, DANIEL L, CORNEL M N. Anti-vibration engineering in internal turning using a carbon nanocomposite damping coating produced by PECVD Process[J]. Journal of Material Engineering and Performance, 2014, 23(2): 506-517.

[14]谭亮红, 陈红, 罗仡科. 阻尼结构对复合结构阻尼性能的影响[J]. 橡胶工业, 2014, 61(2): 84-88.

TAN L H, CHEN H, LUO Y K. Impact factors of damping structural to damping properties of composite structures[J]. Rubber Industry, 2014, 61(2): 84-88 (in Chinese).

[15]夏峰, 刘战强, 宋清华. 约束阻尼结构减振镗杆[J]. 航空学报, 2014, 35(9): 2652-2659.

XIA F, LIU Z Q, SONG Q H. Boring bar with constrained damping[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(9): 2652-2659(in Chinese).

[16]UR-RASHID M. Characterization of dynamic elastic modulus and damping property of CNx coating material by experimental modal analysis and finite element approach[D]. Stockholm： KTH Royal Institute of Technology, 2012： 24-33.

[17]RIVIN E I, KANG H. Enhancement of dynamic stability of cantilever tooling structures[J]. International Journal of Machine Tools and Manufacture, 1992, 32(4): 539-561.

[18]MARYNOWSKI K, KAPITANIAK T. Kelvin-Voigt versus Bürgers internal damping in modeling of axially moving viscoelastic web[J]. International Journal of Non-Linear Mechanics, 2002, 37(7): 1147-1161.

[19]KANASE S S, PATIL J S, JADHAV S M. Improvement of Ra value of boring operation using passive damper[J]. The International Journal of Engineering and Science, 2013, 2(7): 103-108.

[20]王军, 吴凤和. 层状复合结构镗刀杆设计与性能研究[J]. 中国机械工程, 2013, 24(6): 711-715.

WANG J, WU F H. Design and research of composite layered boring bar[J]. China Mechanical Engineering, 2013, 24(6): 711-715 (in Chinese).

[21]何将三. 层复合阻尼镗杆的动力学分析[J]. 中国有色金属学报, 1995, 5(3): 144-148.

HE J S. Dynamics analysis of composite damping boring bar[J]. Chinese Journal of Nonferrous Metals, 1995, 5(3): 144-148 (in Chinese).

[22]BALL III G L, SALYER I O. Development of a viscoelastic composition having superior vibration-damping capability[J]. The Journal of the Acoustical Society of America, 1966, 39(4): 663-673.

[23]DAGHINI L, ARCHENTI A, NICOLESCU C M. Design, implementation and analysis of composite material dampers for turning operations[J]. World Academy of Science, Engineering and Technology, 2009, 53(4): 613-620.

[24]杨昆, 于英华. 泡沫铝/环氧树脂复合材料阻尼性能的研究[J]. 热加工工艺, 2013, 42(16): 110-112.

YANG K, YU Y H. Research on properties of aluminum foam/epoxy composite damping material[J]. Hot Working Technology, 2013, 42(16): 110-112 (in Chinese).

[25]FU Q, LORITE G S, RASHID M U. Suppressing tool chatter with novel multi-layered nanostructures of carbon based composite coatings[J]. Journal of Materials Processing Technology, 2015, 223(15): 292-298.

刘洋男， 硕士研究生。主要研究方向： 减振刀杆。

E-mail: sduliuyang11@gmail.com

刘战强男， 博士， 教授， 博士生导师。主要研究方向： 高速/高效/高性能切削加工。

Tel: 0531-88393206

E-mail: melius@sdu.edu.cn

宋清华男， 博士， 副教授。主要研究方向： 高速切削振动及控制。

E-mail: ssinghua@sdu.edu.cn

Optimization and damping performance of constrained dampingboring bar

LIU Yang, LIU Zhanqiang*, SONG Qinghua

Key Laboratory of High Efficiency and Clean Mechanical Manufacture, Ministry of Education, School of Mechanical Engineering, Shandong University, Jinan250061, China

The constrained damping boring bar can effectively reduce the cutting chatter affecting the surface quality and accuracy in hole machining, but the effect is not significant because the mechanism has not been fully found out. The theoretical and experimental research of the structure optimization, optimal material selection and vibration damping characteristic of the constrained damping boring bar is finished in this paper. Firstly, the dynamics model of the constrained damping boring bar is established through Kelvin-Voigt’s viscoelastic mechanics model theory, and it is proved that the increase of static stiffness and loss factor of the boring bar can enhance the vibration damping performance to improve the quality of machining. Secondly, structure optimization and optimal material selection are completed based on the static stiffness and loss factor theory formula, and the result shows that there is an optimal size range that can reduce the vibration on the main working frequency domain, then it is shown that the elastic modulus of damping layer should be reduced while the elastic modulus of constraining layer and the material loss factor of damping layer should be increased. Finally, four constrained damping boring bars with different materials are designed and manufactured, and the modal experimental results of the static stiffness and loss factor have little difference with the theoretical calculation results. Further study of the influence of material and cutting parameters on the vibration damping performance in machining shows that constrained damping boring bars can effectively reduce the radial vibration to improve the surface quality. The radial vibration of constrained damping boring bars with different materials has great differences in cutting process, and the radial vibration acceleration of the optimized steel-PMMA-carbide boring bar is smaller and more stable at different cutting depths and spindle speeds.

constrained damping; loss factor; structure optimization; modal experiment; cutting stability

2015-07-17； Revised： 2015-08-05； Accepted： 2015-08-28； Published online： 2015-09-0716：18

s: National Natural Science Foundation of China (51425503, 51375272, U1201245)； Major Science and Technology Program of High-end CNC Machine Tools and Basic Manufacturing Equipment (2015ZX04005008)； Taishan Scholar Special (TS20130922)

. Tel.： 0531-88393206E-mail: melius@sdu.edu.cn

2015-07-17； 退修日期： 2015-08-05； 录用日期： 2015-08-28；

时间： 2015-09-0716：18

www.cnki.net/kcms/detail/11.1929.V.20150907.1618.004.html

国家自然科学基金 (51425503， 51375272， U1201245)； 高档数控机床与基础制造装备科技重大专项 (2015ZX04005008)； 泰山学者专项 (TS20130922)

.Tel.： 0531-88393206E-mail: melius@sdu.edu.cn

10.7527/S1000-6893.2015.0241

V261； TG713+.3

A

1000-6893(2016)06-1992-11

引用格式： 刘洋， 刘战强， 宋清华． 约束阻尼型镗杆的优化及减振性能[J]． 航空学报, 2016, 37(6): 1992-2002. LIU Y, LIU Z Q, SONG Q H. Optimization and damping performance of constrained damping boring bar[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6): 1992-2002.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

URL： www.cnki.net/kcms/detail/11.1929.V.20150907.1618.004.html