两种基于方差的全局灵敏度分析W指标改进算法

巩祥瑞， 吕震宙， 左健巍

西北工业大学 航空学院， 西安　710072



两种基于方差的全局灵敏度分析W指标改进算法

巩祥瑞， 吕震宙*， 左健巍

西北工业大学 航空学院， 西安710072

在全局灵敏度分析(SA)中，基于方差的灵敏度分析指标(包括Sobol指标和W指标)应用广泛。其中Sobol指标是将输入随机变量固定于特定点时，求得其对输出响应量的平均影响；而W指标求解当输入随机变量在各自分布区间上缩减变化时，输入变量对输出响应量的影响程度。相比Sobol指标，W指标所反映的信息更加全面。但目前对W指标的求解方法还比较欠缺，双层重复抽样蒙特卡罗(DLRS MC)方法和双层一次抽样蒙特卡罗(DLSS MC)方法是两种传统的求解方法。针对W指标的求解问题，提出了两种新算法：改进的蒙特卡罗模拟(AMCS)和基于稀疏网格积分(SGI)的方法。AMCS只需抽取一组样本便可计算出所有变量的各阶W指标，由于该方法是通过筛选策略来计算条件区间上的方差，避免了DLSS MC法中由于小数取整带来的计数误差，从而提高了计算W指标的精度。基于SGI的方法则利用稀疏网格积分来计算三重矩进而得到W指标，由于该方法继承了稀疏网格积分的高效性，因而进一步提高了W指标的计算效率。最后，给出了两个数值算例和一个工程算例，用于验证所提方法求解W指标的准确性和高效性。

全局灵敏度分析； Sobol指标； W指标； 改进的蒙特卡罗模拟法； 稀疏网格积分法

灵敏度分析(SA)主要研究结构输入随机变量对输出响应量的影响程度，它可分为局部灵敏度(Local SA)和全局灵敏度(Global SA)。局部灵敏度为输入随机变量分布参数在名义值处对输出响应的影响程度[1-3]，它不能全面反映输入变量的不确定性是如何影响输出响应特征的[4]；全局灵敏度则比较全面地反映了这些信息[5]。近些年，已经提出了许多全局灵敏度分析方法。Helton[6-7]和Saltelli[8]等提出了非参数方法，Chun[9]、Liu[10]和Borgonovo[11]等分别提出了基于矩独立的方法，Cui[12]和Li[13]等提出了基于失效概率的方法，Sobol[14]和Saltelli[15-17]等提出了基于方差的全局灵敏度指标。其中基于方差的全局灵敏度指标因其能简单有效地反映输入变量对输出响应量的影响而得到了广泛应用。

一般地，基于方差的全局灵敏度指标分为Sobol指标和W指标。Sobol指标基本思想是固定某一或多个输入变量在特定点，求得输入变量按其分布规律取特定点时，对输出响应量的平均影响[16-18]。但在实际应用中，一般不可能将输入变量固定于特定点，而将输入变量缩减到某一个区间上则是可行的。为此，Wei等[19]提出了一种新的基于方差的全局灵敏度分析W指标，该指标在已有指标基础上，将固定点扩展到区间。通过物理解释、几何图形和数学论证，Wei等指出Sobol指标仅反映了输入变量对输出响应量影响的边缘信息，而W指标则能获得输入变量在整个分布区域的各种可能的区间中变化时，对输出响应量的平均影响[20]。

当输入变量由固定点扩展到区间时，所有用于计算Sobol指标的传统方法将不再适用，必须研究新的算法。Wei等[19]提出了3种方法来计算W指标：双层重复抽样蒙特卡罗(DLRS MC)方法，双层一次抽样蒙特卡罗(DLSS MC)方法和态相关参数(SDP)法[21]。为获取满足精度要求的结果，3种方法都必须抽取大量样本点，因此计算量很大，效率较低。针对此问题，本文提出了两种改进算法：改进的蒙特卡罗模拟(AMCS)方法和基于稀疏网格积分(SGI)的方法[22]。AMCS方法只需抽取一组样本点，在计算条件方差时采用筛选法，避免了DLSS MC方法中可能产生小数取整而导致计数误差的问题，因此其计算精度高于DLSS MC方法。基于稀疏网格积分的方法则充分利用了该积分法的高效性，通过采用稀疏网格积分分别来求解不同给定条件下嵌套的三重统计矩来计算W指标，可以在一定程度上提高W指标的计算效率。

论文在综述了W指标的定义及物理意义之后，给出了两种新的求解方法的基本思路及实现步骤，最后用算例验证了所提方法的效率与精度。

1　W指标的定义及解释

W指标是一种基于方差的全局灵敏度指标，它反映了输入变量在所有可能取值区间内取值时对输出性能的平均方差贡献，与基于方差的Sobol指标相比，W指标能够更加全面地反映输入变量对输出性能变异性的贡献。本文的工作旨在建立W指标的高效求解方法，为方便起见，先简要给出W指标的定义及物理意义。

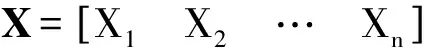
(1)

式中：fXi(·)为Xi的边缘概率密度函数。

当输入变量Xi遍历所有可能取值区间时，它对输出响应方差V(Y)的平均影响可以由式(2)所定义的Wi主指标表达[19]。

(2)

当除Xi外的所有输入变量X～i分布范围缩减到区间U～i时，按照类似的方法可以得到输入变量Xi的W总指标为

(3)

W指标反映了一个(或一组)输入变量对输出响应量方差的贡献程度。W主指标反映了当单个输入变量在其所有可能的分布区间上变化时，输出响应量方差的平均减少量。因此，W主指标越大，输出响应量方差的减少量也越大。W总指标反映了除给定输入变量以外的其他变量在各自区间上变化时，输出响应量方差的平均剩余量。某一输入变量的W总指标趋近于零时，说明该输入变量的区间改变不会引起输出响应量方差的变化。

由定义可以看到，在计算W指标时，主要任务是求得输入变量在固定区间上的条件方差，下面就围绕W指标的求解建立AMCS方法和基于稀疏网格积分的方法。

2　计算W指标的改进算法

设n维输入变量X的样本数为N1，某一维输入变量变化区间的样本数为N2。文献[19]中给出的DLRSMC方法的计算次数为2×n×N1×N2，为了获得较精确的解，抽样数一般都比较大；DLSSMC方法的计算次数为N1，相比于DLRSMC方法，计算量会有所减少,但存在较大误差。

本文将给出两种求解W指标的新算法：① 针对DLSSMC方法中有可能出现的样本计数误差，提出了基于样本筛选的AMCS方法，该方法通过筛选出给定约束区间的样本来计算条件方差，准确得到约束区间的条件样本，在计算量与DLSSMC方法相同的条件下得到了更为精确的条件方差及最终的W指标计算结果；② 利用稀疏网格积分的高效性来求解W指标，建立基于稀疏网格积分的W指标求解方法。两种方法的具体实现过程如下所述。

2.1AMCS方法

1) 根据输入变量的联合概率密度函数fX(x)产生的样本A(维数为N1×n)为

(4)

2) 根据给定分位数qi(1)和qi(2)的分布特性，可先产生qi(1)和qi(2)的样本矩阵Qi(维数为N2×2)为

(5)

由分位数样本矩阵就能得到Xi的固定区间矩阵Ui(维数为N2×2)为

(6)

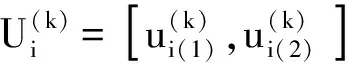
条件方差的计算表达式为

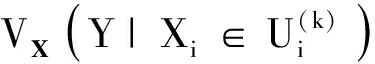
(7)

当k=N2时，停止计算，并得到W主指标的估计值为

(8)

以上所述AMCS方法可以很容易扩展到W总指标的计算。此方法总的输出响应计算次数为N1。该方法避免了采用DLSSMC方法时取整造成样本点的计数误差，从而使计算精度有所提高。

2.2基于稀疏网格积分的方法

稀疏网格积分方法的基本思想是以Smolyak准则为基础，通过采用合适的一维求积公式的张量积组合来构建多维求积公式，可以避免维数灾难。求解W指标的过程可以看做是求矩的三重嵌套积分。以下给出该方法的具体求解过程：

1) 产生Xi的固定区间列阵Ui。

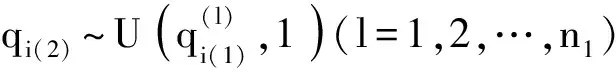
③ 由qi(1)和qi(2)的稀疏网格积分节点产生输入变量Xi的固定区间Ui。

(9)

2) 计算输出响应量方差V(Y)。

用稀疏网格积分法按概率密度函数fX(x)抽取X的样本点(维数为Nk×n)和每一个样本节点xi对应的权重wi(i=1,2,…,Nk)，可得输出响应量方差V(Y)为

(10)

(11)

式中：g(xi)为样本节点xi对应的输出响应量。

3) 当输入变量Xi固定于某一区间时计算输出响应量的条件方差。

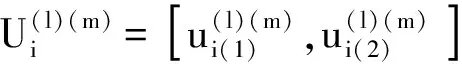
(12)

3　算　例

3.1数值算例1

考虑某结构系统，功能函数为g(X)=exp(0.2X1+1.4)-X2+3X3输入变量相互独立，且均服从标准正态分布，即Xi～N(0,1)(i=1,2,3)。

采用SGI、AMCS、DLSSMC和DLRSMC方法求得W指标如表1所示。表中也给出了每种方法计算功能函数的总次数。DLRSMC方法作为对比参照解，由表1可知SGI和AMCS方法的计算结果与DLRSMC方法计算结果接近。图1 为4种方法计算结果随抽样数变化的数值收敛曲线图。在保证计算所得数据均收敛条件下，SGI和AMCS方法计算量都小于DLRSMC方法，其中AMCS方法相比DLSSMC方法精度有所提高，SGI方法在保证精度要求的前提下，计算效率得到很大提高。

由表1可知，4种方法计算W主指标的重要性排序结果相同，均为X3>X2>X1。这说明当固定3个变量在它们各自的分布区间时，X3对输出响应方差的平均减少量贡献最大。X1和X2的W主指标较小，这说明X1和X2在它们各自的分布区间缩减变化，对输出响应量方差的平均影响程度不大。4种方法计算W总指标排序为X3>X2>X1，这表明当固定除X3外，其他所有变量时，X3对输出量的方差影响最显著。因此，在实际应用中，应重点关注X3对结构输出造成的影响。

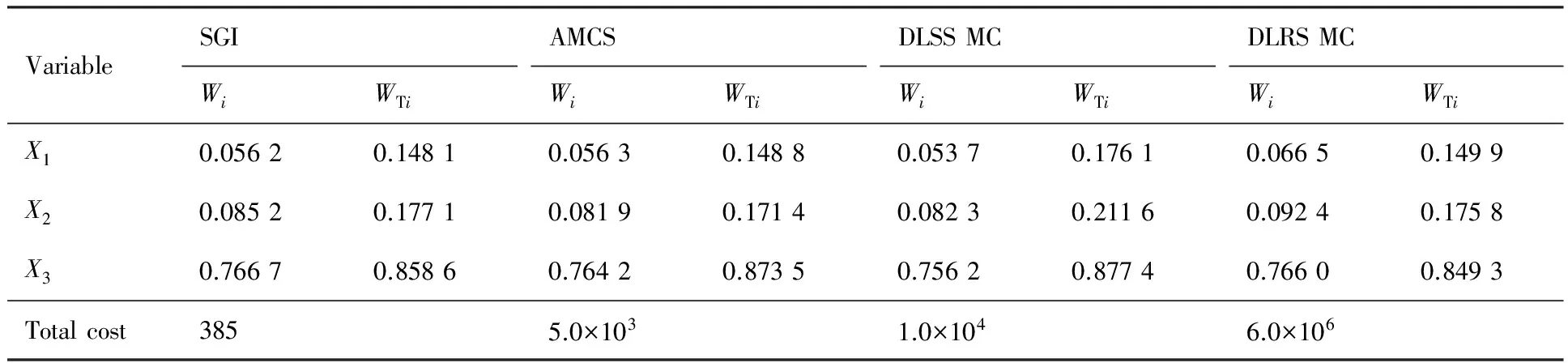
表1　数值算例1基于方差全局灵敏度分析W指标

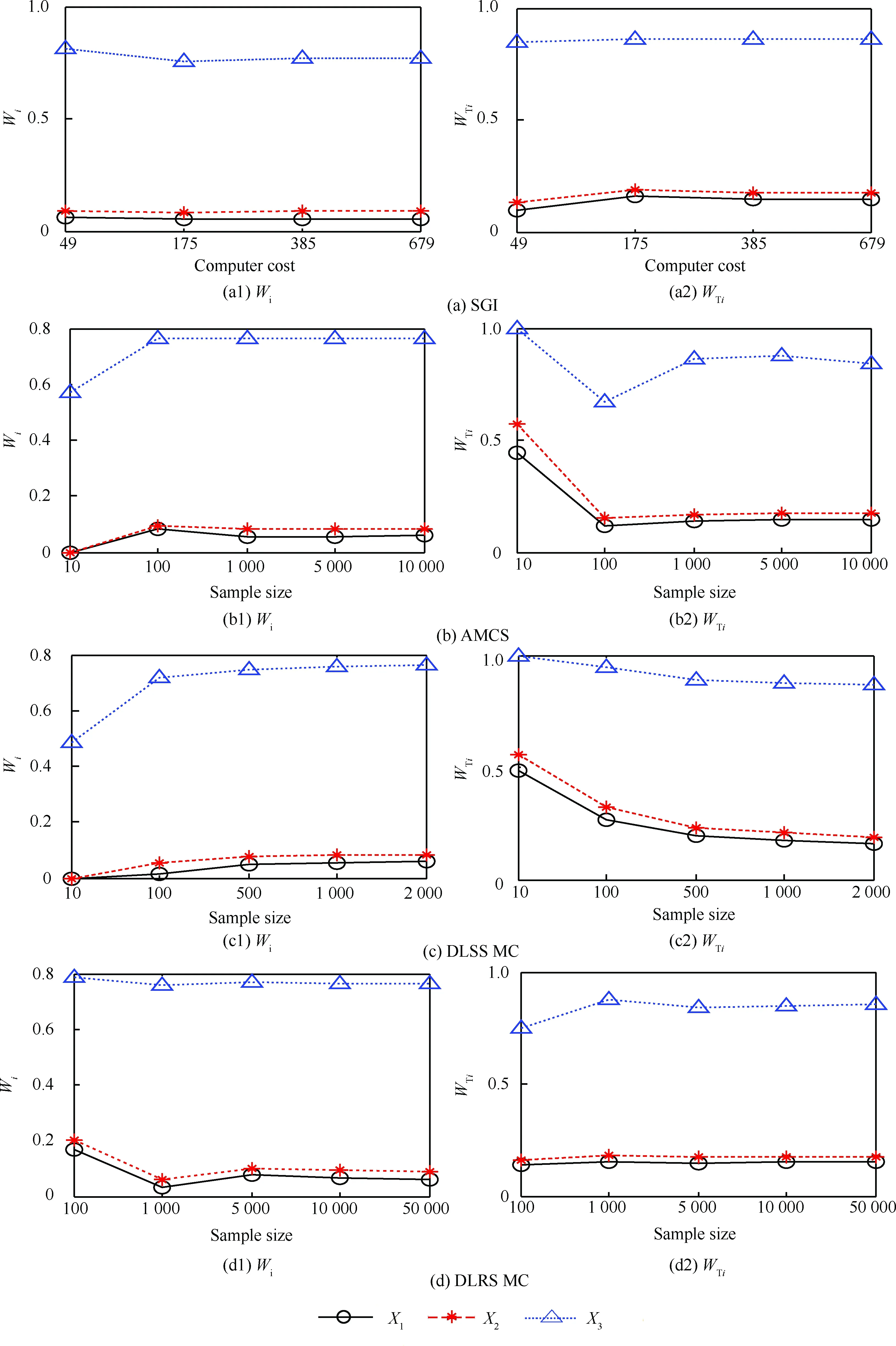
图1　分别应用SGI、AMCS、DLSS MC、DLRS MC计算数值算例1各输入变量的W主指标和W总指标随抽样数变化的数值收敛图Fig.1　Schematic comparison of convergence rate of W-indices of numerical Example 1 estimated by SGI, AMCS, DLSS MC and DLRS MC procedure with respect to sample size

3.2数值算例2

采用SGI、AMCS、DLSSMC和DLRSMC方法求得的W指标如表2所示。从表中计算结果可以看出，由4种方法计算所得变量的W指标排序都相同，均为X2>X3>X1>X4。X2的W主指标和W总指标均为最大，这表明X2对输出量方差的影响程度最大。而X1、X4的W主指标数值接近于零，W总指标也很小，这表明当固定X1和X4在它们各自的减缩区间时，对输出量方差的影响程度很小。

图2为4种方法计算W指标的数值收敛图。根据图2中各数值收敛曲线走势，得到每种方法计算W指标的结果和计算次数列于表2中。由表2可知，SGI方法和AMCS方法所得计算结果相比于DLRSMC方法，误差较小，满足精度要求；同时SGI、AMCS、DLSSMC和DLRSMC的计算次数依次为1 161、1.0×104、1.0×104和8×106。可见SGI和AMCS方法相比于DLRSMC方法计算量减少很多，特别是SGI方法计算效率提高显著。

表2　数值算例2基于方差全局灵敏度分析W指标

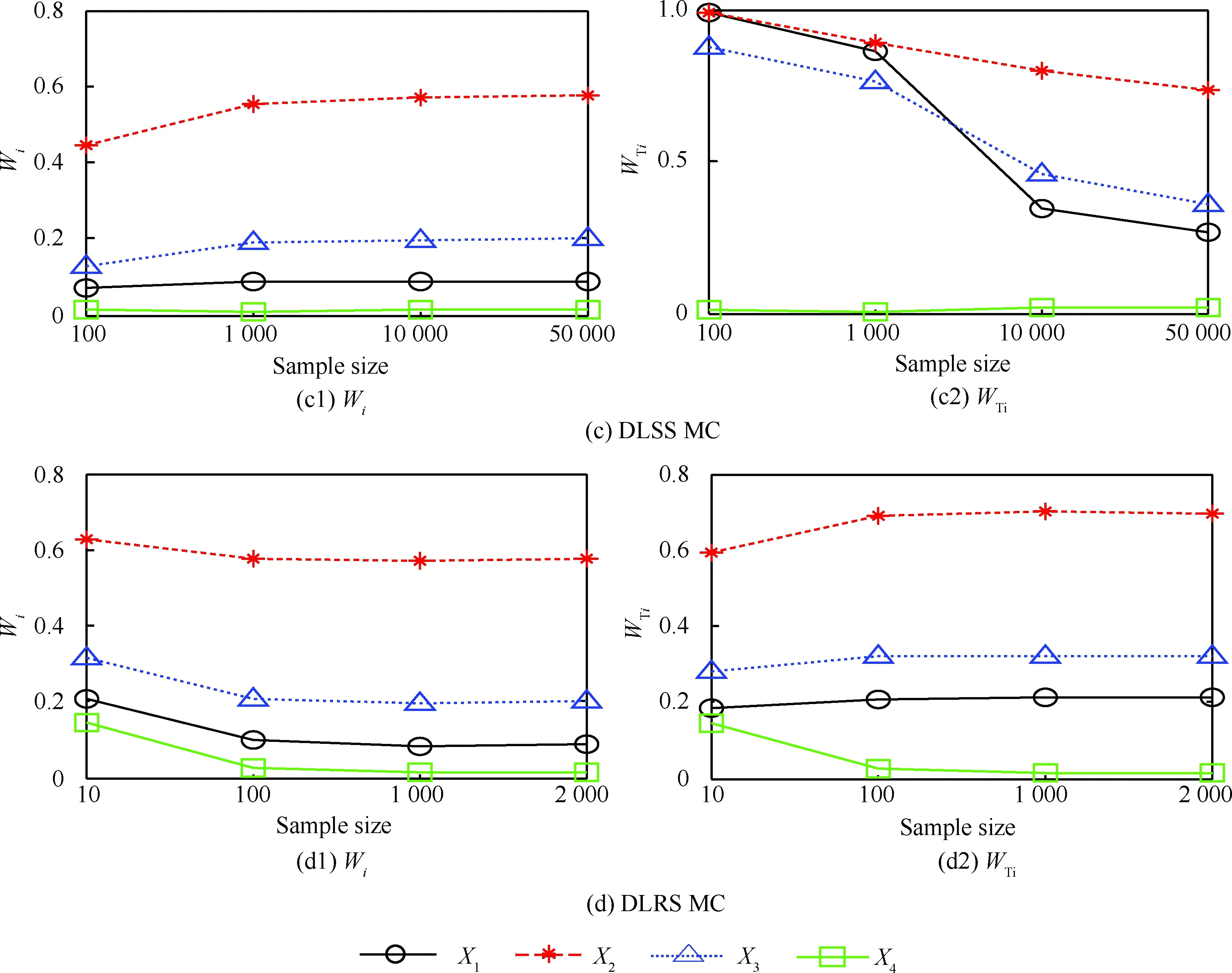
图2　分别应用SGI、AMCS、DLSS MC、DLRS MC计算数值算例2各输入变量的W主指标和W总指标随抽样数变化的数值收敛图Fig.2　Schematic comparison of convergence rate of W-indices of numerical Example 2 estimated by SGI, AMCS, DLSS MC and DLRS MC procedure with respect to sample size

3.3工程算例

图3为一个屋架结构，屋架上的弦杆和其他压杆采用钢筋混凝土杆，下弦杆和其他拉杆采用钢杆。设屋架承受均布载荷q作用，将均布载荷q化成节点载荷后有P=ql/4。结构力学分析可得，C点沿垂直地面方向的位移为

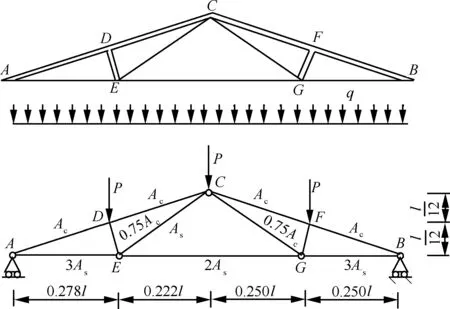
图3　屋架结构简单示意图Fig.3　Sketch map of a roof truss

式中：Ac、Ec、As、Es和l分别为混凝土和钢杆的横截面积、弹性模量和长度。假设所有随机变量均服从独立的正态分布，它们的分布参数如表3所示。

采用SGI、AMCS、DLSS MC和DLRS MC这4种方法计算W指标如表4所示。根据图4所示的各种算法数据收敛曲线图，在表4中给出了4种算法的计算结果和调用功能函数总次数，其中DLRS MC作为对比参照解，它的计算次数最大为1.2×107。 DLSS MC的计算次数为5×104，但该方法计算W总指标的误差较大，故未列出。原因是在计算W总指标时，条件方差的计算需要在内层进行，当输入变量的固定区间很小时，用于计算条件方差的抽样点就会特别少，而该方法又会在获取抽样点时由于小数取整舍弃一些抽样点，这都会增加条件方差的计算误差，从而使计算所得W总指标不准确，因此DLSS MC不适用于计算高阶W指标。AMCS方法很好地克服了DLSS MC方法的缺点，在计算量相同的条件下，进一步提高了W指标的计算精度。SGI方法的计算次数仅为4 165，同其他3种方法相比，在满足精度要求的前提下，计算效率得到了很大提高。

表3屋架结构随机变量的分布参数

Table 3Distribution parameters of random variables of roof truss

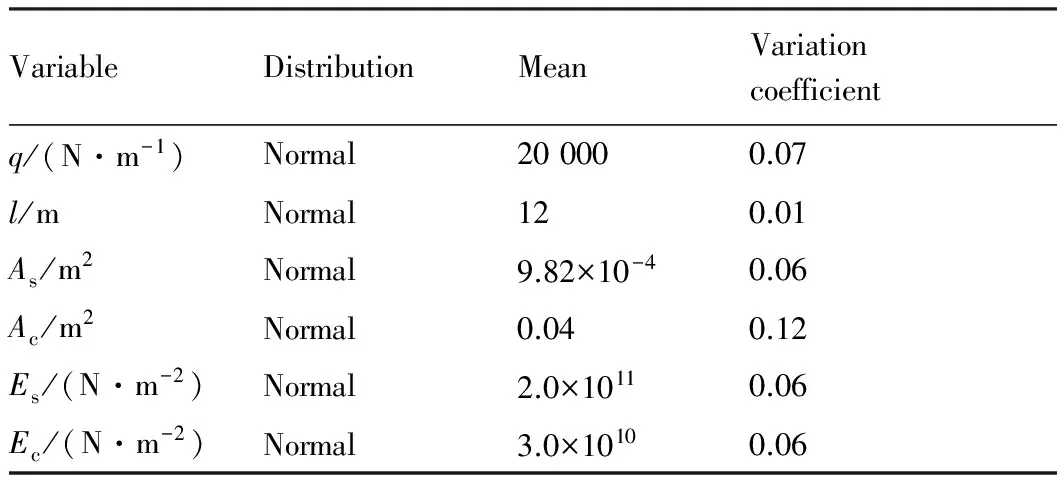
VariableDistributionMeanVariationcoefficientq/(N·m-1)Normal200000．07l/mNormal120．01As/m2Normal9．82×10-40．06Ac/m2Normal0．040．12Es/(N·m-2)Normal2．0×10110．06Ec/(N·m-2)Normal3．0×10100．06

由表4中数据可以看出，各变量的W主指标和W总指标重要性排序相同：q>Ac>Es>As>l>Ec。表明当各变量区间缩减时，q对结构输出的方差减少量贡献最大,Ec对结构输出的方差减少量贡献最少。因此在实际工程应用中，对该屋架结构，应重点关注屋架所承受均布载荷q的大小，混凝土的横截面积Ac对屋架结构稳定性影响也较大，而混凝土的弹性模量Ec对其影响较小，可简化处理。

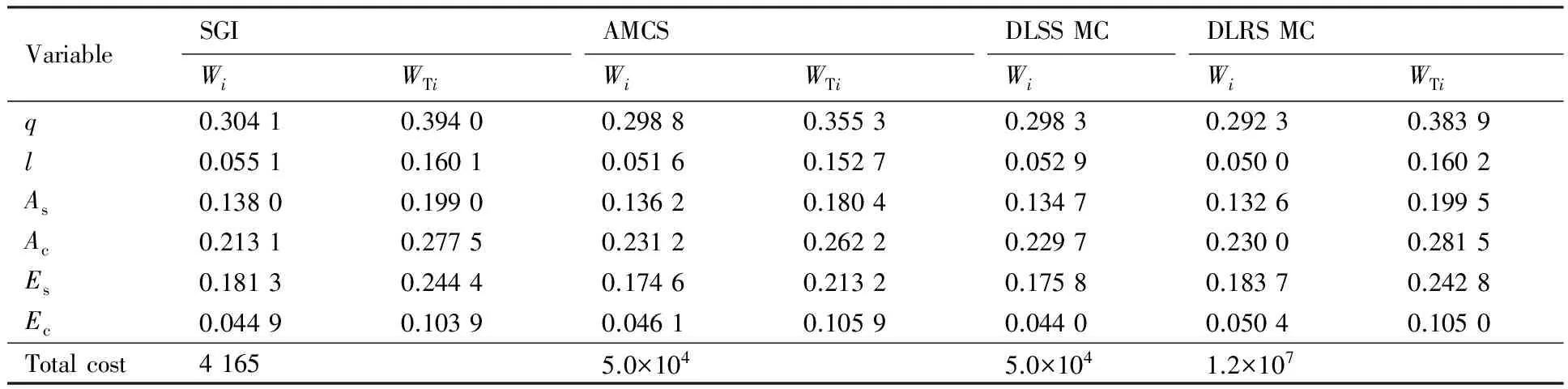
表4　工程算例基于方差全局灵敏度分析W指标

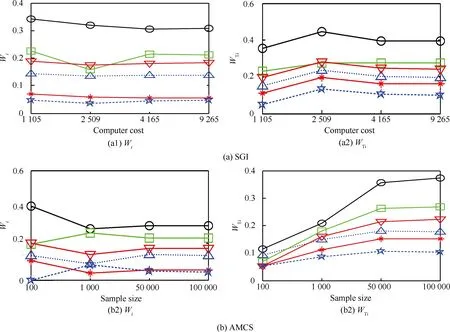
图4　分别应用SGI、AMCS、DLSS MC、DLRS MC计算工程算例各输入变量的W主指标和W总指标随抽样数变化的数值收敛图Fig.4　Schematic comparison of convergence rate of W-indices of engineering example estimated by SGI, AMCS, DLSS MC and DLRS MC procedure with respect to sample size

4　结　论

1) AMCS方法采用样本筛选策略来计算条件方差，避免了DLSS MC方法中由于小数取整造成的计数误差。

2) 在计算量相同的情况下，AMCS方法的精度高于DLSS MC方法的。

3) SGI方法采用数值积分来求解W指标中的三重统计矩，可以直接应用于求解一般维数不高的工程问题中，提高计算效率；但由于该方法未能完全克服输入变量维数的影响，因此对于大型高维复杂工程问题，SGI方法计算量可能会超过DLSS MC方法和AMCS方法。

[1]ZIO E, PODOFILLINI L. Accounting for components interactions in the differential importance measure[J]. Reliability Engineering & System Safety, 2006, 91(10-11): 1163-1174.

[2]DO VAN P, BARROS A, BERENGUER C. Differential importance measure of Markov models using perturbation analysis[C]//European Safety and Reliability Conference (ESREL 2009). Abingdon, UK: Taylor & Francis, 2009: 981-987.

[3]BORGONOVO E, APOSTOLAKIS G E. Comparison of global sensitivity analysis techniques and importance measures in PSA[J]. Reliability Engineering & System Safety, 2003, 79(2): 175-185.

[4]VON GRIENSVEN A, MEIXNER T, GRUNWALD S, et al. A global sensitivity analysis tool for the parameters of multi-variable catchment models[J]. Journal of Hydrology, 2006, 324(1-4): 10-23.

[5]SALTELLI A. Sensitivity analysis for importance assessment[J]. Risk Analysis, 2002, 22(3): 579-590.

[6]HELTON J C, DAVIS F J. Latin hypercube sampling and the propagation of uncertainty in analyses of complex systems[J]. Reliability Engineering & System Safety, 2003, 81(1): 23-69.

[7]HELTON J C. Uncertainty and sensitivity analysis techniques for use in performance assessment for radioactive waste disposal[J]. Reliability Engineering & System Safety, 1993, 42(2): 327-367.

[8]SALTELLI A, MARIVOET J. Non-parametric statistics in sensitivity analysis for model output: A comparison of selected techniques[J]. Reliability Engineering & System Safety, 1990, 28(2): 229-253.

[9]CHUN M H, HAN S J, TAK N I L. An uncertainty importance measure using a distance metric for the change in a cumulative distribution function[J]. Reliability Engineering & System Safety, 2000, 70(3): 313-321.

[10]LIU H, CHEN W, SUDJIANTO A. Relative entropy based method for probabilistic sensitivity analysis in engineering design[J]. Journal of Mechanical Design, 2006, 128(2): 326-336.

[11]BORGONOVO E. A new uncertainty importance measure[J]. Reliability Engineering & System Safety, 2007, 92(6): 771-784.

[12]CUI L J, LU Z Z, ZHAO X P. Moment-independent importance measure of basic random variable and its probability density evolution solution[J]. Science China Technological Sciences, 2010, 53(4): 1138-1145.

[13]LI L Y, LU Z Z, FENG J, et al. Moment-independent importance measure of basic variable and its state dependent parameter solution[J]. Structural Safety, 2012, 38: 40-47.

[14]SOBOL’ I M. Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J]. Mathematics and Computers in Simulation, 2001, 55(1): 271-280.

[15]SALTELLI A, ANNONI P, AZZINI I, et al. Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index[J]. Computer Physics Communications, 2010, 181(2): 259-270.

[16]ARCHER G E B, SALTELLI A, SOBOL I M. Sensitivity measures, ANOVA-like techniques and the use of bootstrap[J]. Journal of Statistical Computation and Simulation, 1997, 58(2): 99-120.

[17]SOBOL’ I M. On sensitivity estimation for nonlinear mathematical models[J].Matematicheskoe Modelirovanie, 1990, 2(1): 112-118.

[18]SALTELLI A, TARANTOLA S. On the relative importance of input factors in mathematical models: Safety assessment for nuclear waste disposal[J]. Journal of the American Statistical Association, 2002, 97(459): 702-709.

[19]WEI P, LU Z Z, SONG J. A new variance-based global sensitivity analysis technique[J]. Computer Physics Communications, 2013, 184(11): 2540-2551.

[20]TARANTOLA S, KOPUSTINSKAS V, BOLADO-LAVIN R, et al. Sensitivity analysis using contribution to sample variance plot: Application to a water hammer model[J]. Reliability Engineering & System Safety, 2012, 99: 62-73.

[21]RATTO M, PAGANO A, YOUNG P. State dependent parameter metamodelling and sensitivity analysis[J]. Computer Physics Communications, 2007, 177(11): 863-876.

[22]BARTHELMANN V, NOVAK E, RITTER K. High dimensional polynomial interpolation on sparse grids[J]. Advances in Computational Mathematics, 2000, 12(4): 273-288.

巩祥瑞男， 硕士研究生。主要研究方向： 飞行器设计及可靠性工程。

Tel: 029-88460480

E-mail: gxrui1991@163.com

吕震宙女， 博士， 教授， 博士生导师。主要研究方向： 飞行器设计及可靠性工程。

Tel: 029-88460480

E-mail: zhenzhoulu@nwpu.edu.cn

左健巍男， 硕士研究生。主要研究方向： 飞行器设计及可靠性工程。

Tel: 029-88460480

E-mail: jianweizuo@mail.nwpu.edu.cn

Two improved methods for variance-based global sensitivityanalysis’ W-indices

GONG Xiangrui, LYU Zhenzhou*, ZUO Jianwei

School of Aeronautics, Northwestern Polytechnical University, Xi’an710072, China

In the global sensitivity analysis (SA), the variance-based sensitivity indices, such as Sobol’s indices and W-indices, are used widely. Sobol’s indices estimate the average variation of model output when input variables are fixed in their points. W-indices measure the average reduction of model output if input variables are reduced in their distributions. Compared with Sobol’s indices, W-indices include more information. The double loop repeated set Monte Carlo (DLRS MC) and double loop single set Monte Carlo (DLSS MC) are two traditional methods, but these available methods for solving W-indices are still defective. In order to calculate W-indices efficiently, two new methods are presented. They are advanced Monte Carlo simulation (AMCS) and sparse grid integration (SGI)-based method. The AMCS only needs one set of samples to estimate all W-indices. Since screening method is used to estimate the variance in the conditional interval, and the count error induced by taking an integer in DLSS MC can be avoided, the accuracy of AMCS is higher than that of DLSS MC. The SGI-based method estimates W-indices by evaluating threefold statistic moment by SGI, in which the efficiency of the SGI is inherited. Finally, two numerical examples and an engineering example are employed to demonstrate the reasonability and efficiency of the presented methods.

global sensitivity analysis; Sobol’s indices; W-indices; advanced Monte Carlo simulation method; sparse grid integration

2015-04-10； Revised： 2016-01-05； Accepted： 2016-03-22； Published online： 2016-03-2516:07

s： National Natural Science Foundation of China (51475370)； Fundamental Research Funds for the Central University (3102015BJ(II)CG009)

. Tel.： 029-88460480E-mail: zhenzhoulu@nwpu.edu.cn

2015-04-10； 退修日期： 2016-01-05； 录用日期： 2016-03-22；

时间： 2016-03-2516:07

www.cnki.net/kcms/detail/11.1929.V.20160325.1607.002.html

国家自然科学基金 (51475370)； 中央高校基本科研业务费专项资金 (3102015BJ(II)CG009)

.Tel.： 029-88460480E-mail: zhenzhoulu@nwpu.edu.cn

10.7527/S1000-6893.2016.0090

V215.7; TB114.3

A

1000-6893(2016)06-1888-11

引用格式： 巩祥瑞， 吕震宙， 左健巍． 两种基于方差的全局灵敏度分析W指标改进算法[J]． 航空学报, 2016, 37(6): 1888-1898. GONG X R, LYU Z Z, ZUO J W. Two improved methods for variance-based global sensitivity analysis’ W-indices[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6): 1888-1898.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

URL： www.cnki.net/kcms/detail/11.1929.V.20160325.1607.002.html