用于可压缩自由剪切流动的湍流混合长度

徐晶磊， 宋友富， 张扬， 白俊强

1.北京航空航天大学 能源与动力工程学院， 北京　100083 2.西北工业大学 航空学院， 西安　710072



用于可压缩自由剪切流动的湍流混合长度

徐晶磊1,*， 宋友富1， 张扬2， 白俊强2

1.北京航空航天大学 能源与动力工程学院， 北京100083 2.西北工业大学 航空学院， 西安710072

抓住可压缩流动变密度特性，构造出基于有效涡量的三维von Karman混合长度。湍流模型采用仅依赖湍动能k的单方程KDO(Kinetic Dependent Only)模型，引入新构造的混合长度替换旧尺度得到CKDO模型。为了验证其描述可压缩自由剪切湍流的能力，选择无壁面束缚、密度梯度大和可压缩效应强的自由剪切混合层为算例，其对流马赫数Mac=0.8。计算结果表明，KDO模型对混合层的速度分布有着良好的控制和模拟，而经可压缩修正后的CKDO模型与原模型及其他可压缩修正模型相比，所计算的速度分布、主雷诺剪切力和混合层厚度与试验结果更加接近，说明了该混合长度对可压缩混合层这种自由剪切湍流有着良好的刻画能力。

湍流模型； 混合层； 超声速流动； 可压缩性； 数值模拟

早期湍流模式从理论推导到经验参数的标定都是基于不可压缩湍流，目前对不可压缩湍流模式研究已经较为深入，发展也比较成熟。随着社会发展和科学技术的日益成熟，现代飞行器对速度的要求进一步提升，超声速流动甚至是高超声速流动研究变得重要和迫切。当流动马赫数逐渐增加，通常认为马赫数Ma>0.3时，流动不能再作为不可压缩流动处理，而应该作为更为复杂的可压缩流动来分析。以可压缩湍流混合层为代表的自由剪切湍流流动，在很多工程应用当中都有出现，被认为是研究可压缩性对湍流结构影响的典型例子。可压缩自由剪切流动的湍流混合层试验较为普遍，早期Birch和Eggers[1]就对它进行过试验研究，试验结果表明可压缩混合层区别于不可压缩混合层的一个明显特征就是混合层发展缓慢，混合层厚度增长受到抑制。同时，通过Gruber等[2]的试验研究发现，混合层厚度的增长率和平均速度分布曲线可以描述该流动的主要特征，并且在一定区间平均速度分布呈现相似性。

为了进一步研究可压缩自由剪切湍流混合层，本文通过采用传统湍流模型对其进行数值计算来验证各湍流模型对可压缩混合层中流动特性的捕捉能力。Wilcox[3-4]提出的k-ω模型方程，其湍动能方程可以从雷诺平均Navier-Stokes(RANS)框架内精确推导出来，但是对于不封闭的ω是以类比于k方程推导过程来构造输运方程进行封闭，缺乏科学的理论推导，在求解超声速的可压缩湍流问题上不能完整反映其典型的物理特性，即使加入Wilcox可压缩修正的k-ω(W)模型方程[5-6]也不能有很好的普适性。Menter[7]提出的剪切应力输运(SST)模型融合了k-ε和k-ω的所有优点，在求解精度和鲁棒性上都有很好的表现，但是其在平衡湍流中依然保持着经典关系式，在模拟可压缩湍流流动时引入Sarkar等[8]可压缩修正，修正后用SST(S)表示该模型。

本文采用文献[9-12]构造的单方程KDO (Kinetic Dependent Only)模型来研究可压缩湍流混合层，KDO模型是一种代数封闭ε，只求解k方程的一方程湍流模型，它只含有两个可调参数。为了进一步提高其模拟可压缩自由剪切湍流流动的能力，在KDO模型方程的基础上作适当可压缩性修正，构造了一种新的湍流模型方程，把它称之为CKDO模型，并且通过可压缩自由剪切流动的湍流混合层来验证该模型的计算精度。

1　KDO模型介绍

1.1Bradshaw假设的扩展

在边界层区域，湍流主应力τ与湍动能k成正比(Rb=τ/k)，其比值接近于一个常数[13]，在很多剪切流动[14]中也常常将该比值设置为0.3左右。但是随着计算机的发展和直接数值模拟(DNS)数据的完善，该比值已不再是一个恒量，在文晓庆[15]和刘景源[16]等的研究中就指出该比值要根据不同的算例情况应该做适当调整。通过白俊强等[10]的研究表明，在湍流充分发展区域该比值的最大值小于0.29。根据对平板边界层DNS数据的研究，它在截面雷诺数Reθ=4 060上的极值为0.283，那么对于非常远离壁面的自由剪切流动，设置Rb=0.283是合理的。则新的主剪切应力公式定义为

τ=ρ Rbk

(1)

结合两方程模型中剪切应力的计算形式：

τ=μtS

(2)

以此推导出本文采用的涡黏性系数计算公式为

(3)

1.2KDO模型[9]形式

Pk-ρε

(4)

Pk=μtS2

(5)

ε=ε1+ε2

(6)

(7)

(8)

μt=ρ Rbk/S

(9)

(10)

式中：ε为湍动能耗散率；L为湍流混合长度；对于无壁面束缚的混合层Rb=0.283； 湍流耗散系数Cd=0.8。

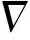
1.3可压缩KDO模型的形式

精确的可压缩湍动能控制方程[18]为

(11)

对于KDO模型，方程右端各项依次分别模化为

(12)

(13)

(14)

(15)

(16)

(17)

涡黏性系数：

(18)

1.4KDO模型的可压缩修正

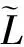
(19)

2　评估算例

Gruber[19]和Goebel[20]等都曾展开过对可压缩湍流混合层流动的试验研究，本文在二维条件下模拟与试验[19]相同的流动情况，主要抓住该流动在混合过程中的一些典型特性。

将试验流动区域简化为如图1所示，上下两股不同来流参数的流体流过一个小的分隔板后相遇混合，上层流体记为1为超声速来流，其参数分别为马赫数Ma1、静压p1、密度ρ1、温度T1、气流速度U1和声速c1；下层流体记为2为亚声速来流，其参数分别为Ma2、p2、ρ2、T2、U2和c2。为了与试验[19]的值对比，本文采用和试验相同的来流参数，具体参数如表1所示。计算生成网格规模为101×401，法向在混合中心线两侧都进行了网格加密处理，网格法向增长率为1.1。

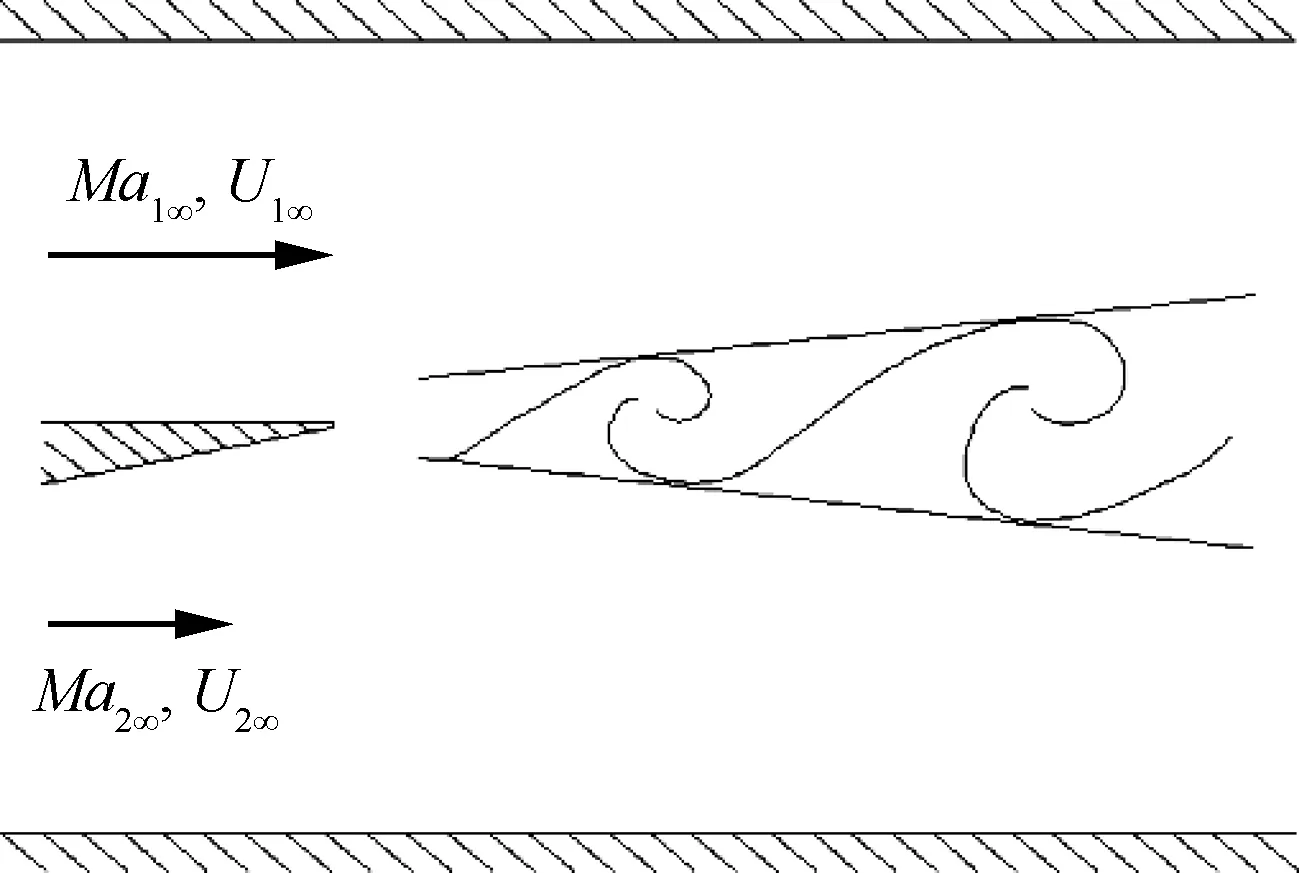
图1　混合层流动示意图Fig.1　Schematic of mixing layer flow

ParameterUpflowDownflowptotal/kPa552．043．4Ttotal/K279289p/kPa40．340．3T/K132285u/(m·s-1)543．091．2c/(m·s-1)230338Ma2．360．27ρ/(kg·m-3)1．060．49μ/(106Pa·s)9．117．7

2.1新旧两种混合长度在混合层内分布规律

图2所示为新旧两种混合长度在混合层内的分布规律，考虑到充分发展情况，截面选取x=120 mm处，混合长度尺度在混合区域与几何流域尺度是一个量级，说明该区域充分发展，具有代表性。从图中可以发现，KDO模型中的不可压缩混合长度在相同的区域始终比新的混合长度的面积范围要大很多，并且波动比较大。而新的混合长度在混合中心处稍大，这是由于此处剪切最严重，两端逐渐趋于稳定，并且总体上比旧尺度小很多。混合长度越大，流动的湍流黏性也就越大，就会影响到流场中的速度分布，从而使湍流模型无法准确捕捉到流场中的流动情况。所以，从图中可知新的长度尺度对应于更小的湍流黏性系数，与可压缩效应引起的湍流度抑制相呼应。

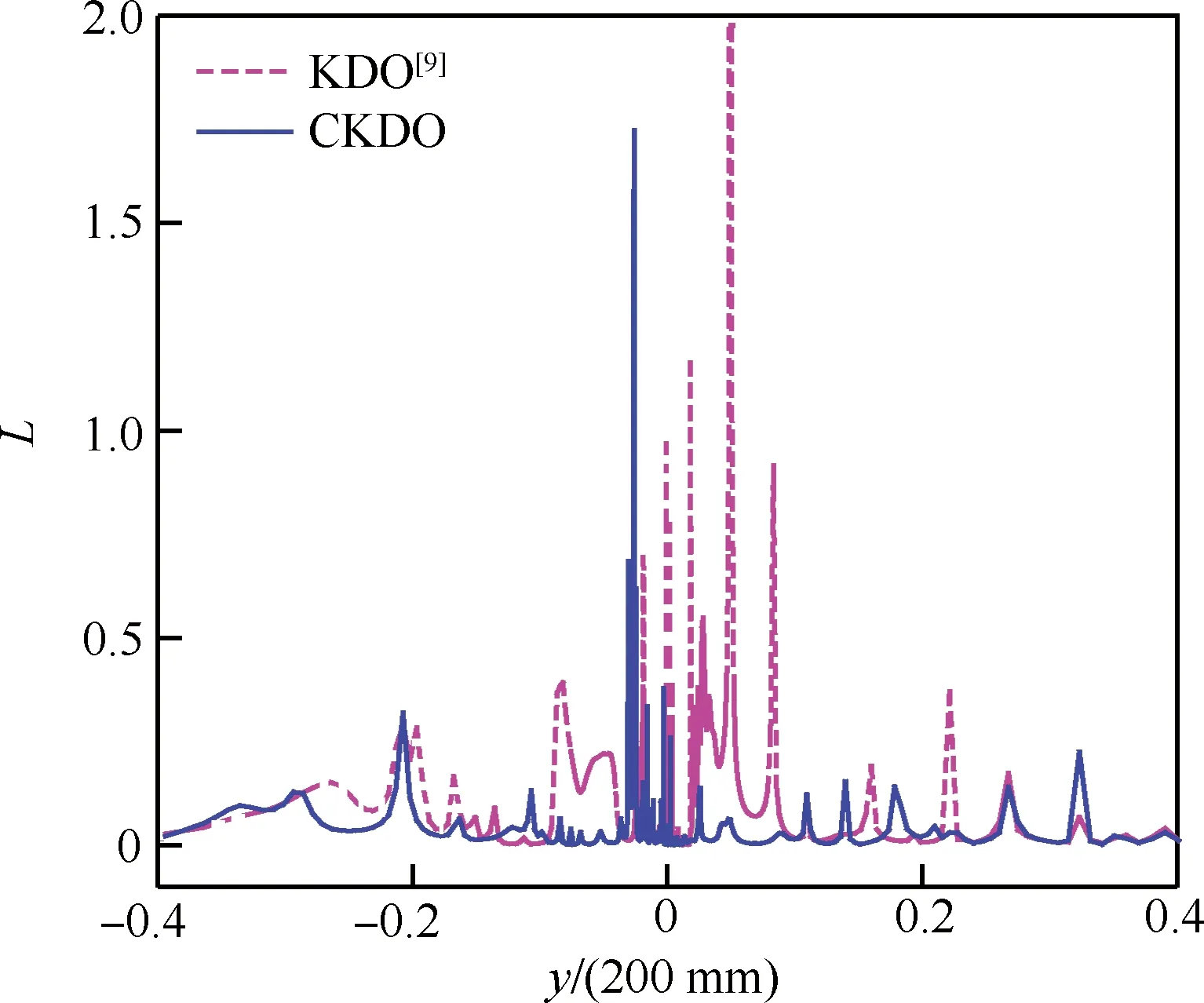
图2　充分发展区域的湍流长度尺度分布 (x=120 mm)Fig.2　Turbulence length scale distributions at fully developed region (x=120 mm)

2.2平均流向速度在混合层厚度上的相似性

对于高雷诺数可压缩自由剪切混合层流动，流动沿主流x方向参数变化远小于y方向，可以采用边界层近似，同时混合层为自由剪切流动，远离壁面，分子黏性项相对于黏性项很小，可以忽略[21]。这里选用Wilcox的k-ω模型以及Menter的SST模型，关于可压缩修正分别引入Wilcox[5-6]和Sarkar等[8]的模化形式。

图3(a)中给出了试验结果[19]，该结果是整个混合层完全混合区(50～170 mm)的平均结果。图中变量b为混合层厚度，定义为速度值U1-0.1(U1-U2)和U2+0.1(U1-U2)在y方向上的距离；y0为混合层中心线位置；U为来流平均速度。从图中可以看到，k-ω模型和k-ω(W)模型的计算结果几乎一致，它们在整个分布上与试验结果符合较好，但是在混合层的两端与试验结果有一定的差别，特别是在混合层靠近低速端，整个曲线较试验值有一个右移。SST模型的计算结果在混合层两端基本能与试验结果吻合，但是在混合层过渡段偏离试验较多，始终在试验曲线值下方。SST(S)模型的计算结果精度在SST模型基础上不但没有改进反而有所下降，遗留了SST模型在混合层过渡段的不准确性，而且在混合层低速端的计算结果质量下降严重。

图3　标准化平均流向速度的相似性Fig.3　Similarity of normalized mean streamwise velocity

图3(b)所示是KDO模型结果和经修正后CKDO模型结果与试验结果的比较，KDO模型的计算结果在混合层低速端以及过渡段与试验结果贴合都比较好，但是其在进入混合层高速端不能很好地过渡，究其原因认为是由于密度变化剧烈而引起的偏差。CKDO模型的计算结果不仅在混合层高低速两端与试验结果吻合得较好，而且在混合层的过段阶段都基本上吻合，可见CKDO模型在可压缩自由剪切湍流流动中对于速度分布有着更好的刻画力。

图3(c)中是不同模型经可压缩性修正后的计算结果与试验值的比较，总体上CKDO的计算结果与试验结果吻合得最好，其次是k-ω(W)模型结果。SST(S)模型较前两者与试验结果误差较大，主要是在混合层过渡阶段偏离试验严重。三者大致上能反映出可压缩自由剪切湍流混合层流动过程中的相似性，某些程度上达到一定的效果，但是这只是一个能反映在流动中各模型平均流向速度对其各自混合层厚度的自我相似程度，并不足以说明其整个流动过程的真实情况，故除此之外，还分析了x=50 mm截面上流向速度的分布。

2.3流向速度在x=50 mm截面上的分布

图4　标准化流向速度x=50 mm截面上的相似性Fig.4　Similarity of normalized streamwise velocity at x=50 mm

由图4(a)可以明显看到，采用SST模型和k-ω模型计算所得结果已经严重偏离试验值，无论是在混合层两端还是整个过渡阶段都已经不能反映出试验[19,22]真实值，这是由于SST模型和k-ω模型的尺度方程是为不可压缩流动设计的，所以在可压缩湍流流动中计算结果不会太好。SST(S)模型和k-ω(W)模型虽然在原模型基础上有所改进，但也基本与试验相差甚远。KDO模型计算结果较上述4种结果都有所改进，在混合层过渡阶段KDO模型的计算结果与试验结果偏离的已经不算严重，大致上已经能模拟出流向速度的分布情况。

图4(b)所示是CKDO模型与KDO模型及试验值的对比，从图中可以看到CKDO模型计算结果可以说与试验值十分贴合了，特别是在整个混合层过渡阶段始终与试验吻合，这相比于其他模型结果是极大改进。主要不足是在混合层两端，较试验结果都偏小，这是由于客观事实导致的，因为试验装置[19]在x=50 mm处上下两壁面有一个扩张，导致气流膨胀加速，由于无法得知其壁面扩张率以及为了简化计算模拟条件，故本文采用上下都是直壁条件，从而导致在该截面处最大速度和最小速度比试验结果都偏小。但是刨除试验装置因素分析可得，两股气流在等截面管道中混合，在某截面处其最大速度必将等于流速较快的那股气流速度值，同理于最小速度。从图中可以发现，CKDO模型计算结果中混合层低速端逐渐趋于0，高速端逐渐趋于1，这也是十分合理的，并且对于湍流混合层主要关注混合区域，从结果看说明CKDO模型能够很好地模拟出流向速度在在x方向上的分布。

2.4平均雷诺应力在混合层厚度上的相似性

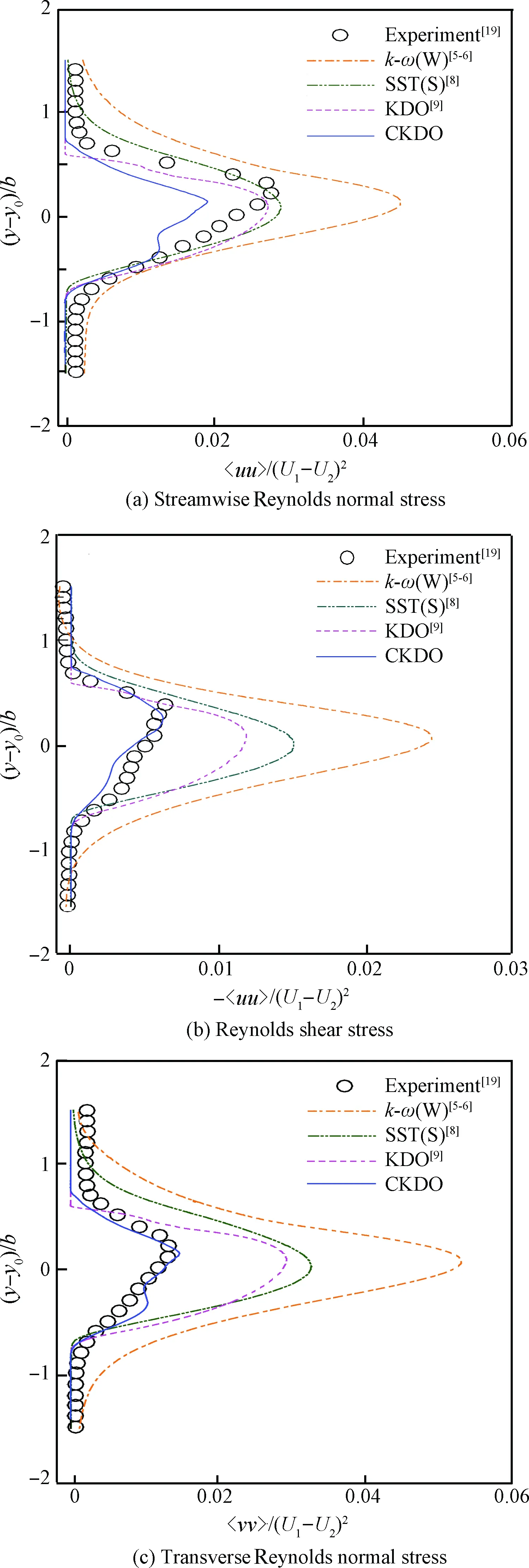
图5　标准化流向雷诺应力的相似性Fig.5　Similarity of normalized streamwise Reynolds stress

图5给出了标准化流向雷诺应力的相似性，u和v分别为流向和法向脉动速度。图5(a)为流向平均(50～170 mm)雷诺正应力的分布，从图中可以看到k-ω(W)模型计算结果与试验差别较大，峰值在试验值两倍左右。KDO模型和SST(S)模型的结果与试验较为贴近，基本能够反映出流向雷诺正应力的分布情况。CKDO模型在混合区前期与试验保持着一定的贴合，但是其在混合区中心的雷诺正应力最大值上与试验有一定差别，比试验峰值略小，这也反映出作为一个由各向同性湍流中发展而来的线性湍流模型对于这种雷诺正应力的精确捕捉还需要作进一步改进。

图5(b)中是法向平均雷诺正应力的分布情况，多数湍流模型计算结果与试验结果相距甚远，尤其是k-ω(W)模型结果已经无法反映出试验的真实值。KDO模型与SST(S)结果大致上一致，但是同样与试验结果偏离严重。CKDO模型对于法向雷诺正应力的模拟则表现出了出色的性能，其结果与试验结果贴合的十分紧密，在整个混合区分布上始终能与试验值保持在一个较高的准确度。

图5(c)是标准化后平均主雷诺剪切力的分布情况，从图中可以发现的共同点是越靠近混合层中心主雷诺剪切力越大，因为中心处剪切最严重。图中可以看到k-ω(W)模型与试验[19]结果偏离严重，它的剪切力峰值已远远大于试验值，并且在整个混合层分布上与试验结果都显得“格格不入”。SST(S)模型计算的结果比k-ω(W)模型稍好，在混合层两侧与试验都有较好的符合程度，但是在混合层内的计算结果尤其在主雷诺剪切力的峰值上与试验结果相差较远，k-ω(W)和SST(S)模型是在特定工况下进行的可压缩修正，所以说对于本文的工况并不一定适用。KDO模型较上述模型的计算结果又有所改观，在剪切力峰值上缩小了与试验结果的差距，但是仍然有较大的误差。试验主雷诺剪切力峰值大概在0.006 33左右，CKDO模型的峰值大概在0.006 2，误差为1.58%，并且主雷诺剪切力在整个混合层的分布上与试验结果始终保持在一个量级上，大部分区域与试验都贴合得较好。CKDO模型在可压缩自由剪切湍流混合层中对主雷诺剪切力的计算精度已远高于其他模型，而主雷诺剪切力在自由剪切流动中是一个重要参考因素。

2.5混合层速度云图及其厚度

图6所示为不同湍流模型模拟整个流动区域的马赫数云图，参考声速为338 m/s。通过该图可以直观地看到整个流动过程混合层形成、发展的情况，包括混合层的厚度大小，厚度增长情况以及速度分布。从图中可以发现经过可压缩修正后的k-ω(W)、SST(S)以及CKDO模型较未修正之前都有一个很大的改进，使整个混合层显得更加规范和相似。

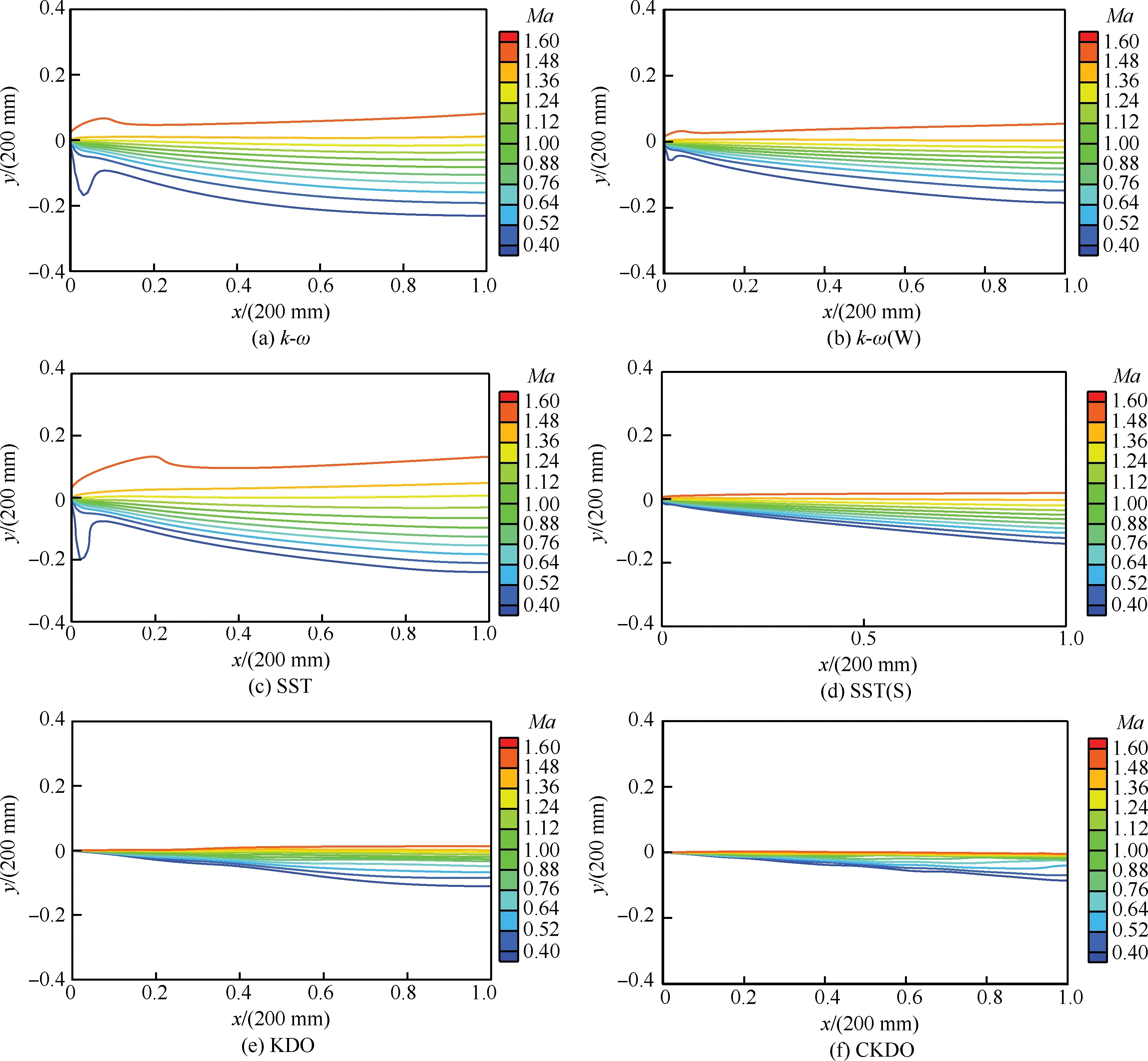
图6　混合层的速度云图Fig.6　Velocity cloud of mixing layer

图7所示为混合层厚度分布图，其厚度增长率取整个完全混合区间平均值。由图可知，k-ω(W)模型计算结果与试验结果偏离严重，其混合层厚度已经远远大于试验值，并且其厚度的增长率都与试验结果相差很远，由此可见k-ω(W)模型在可压缩自由剪切湍流流动中可压缩修正效果并没有体现出来。SST(S)模型的计算结果比k-ω(W)模型的计算结果稍好，但是它的混合层厚度大小还是在试验结果的几倍以上，而且从整体看其混合层厚度增长率也比试验要大很多。KDO模型的计算结果虽然离试验结果差距仍很大，但是比SST(S)和k-ω(W)模型的计算结果都有了很大的进步。从图中明显看到，CKDO模型的计算结果与试验结果最接近，特别是在x=50 mm处的混合层厚度大小，几乎与试验吻合，即使在x=170 mm处厚度也只是相差几毫米，整个厚度增长率也与试验接近。由此可见CKDO模型对于混合层厚度及厚度增长率的模拟能力较强，一定程度上反映出CKDO模型在可压缩自由剪切湍流混合层中的优越性能。

图7　混合层厚度Fig.7　Mixing layer thickness

3　结　论

KDO模型是一个仅仅依赖湍动能输运方程的湍流求解模型，整个模型只含两个可调经验参数，来自于对平板边界层某一切面的精细化标定，并且该数据完全来自于DNS，这就使KDO模型的立论基础和经验参数的标定具有高保真特性。基于KDO模型进行适当可压缩修正构造了CKDO模型方程，通过对可压缩自由剪切湍流混合层的数值模拟，结果表明：

1) 考察标准化后的平均速度在混合层厚度上的相似性以及在x=50 mm截面处流向速度的分布情况，KDO模型对于速度分布的模拟细节较为精确，经过可压缩修正后的CKDO模型则表现得更为完美，模拟结果与试验值贴合得都比较好。

2) 考察自由剪切湍流混合层中平均雷诺应力的相似性及其分布，总体而言，KDO模型比SST(S)和k-ω(W)模型的计算结果都更为接近试验值，而CKDO模型的计算结果与试验值最贴近，特别是在主雷诺剪切力与法向雷诺正应力分布上与试验值吻合较好。

3) 在混合层厚度的模拟计算中，SST(S)和k-ω(W)模型的计算结果与试验值偏离严重，KDO模型比前两者计算结果稍好，CKDO模型结果与试验值符合得最好，很好地反映了混合层的厚度及其增长情况。

算例验证表明，KDO模型在可压缩自由剪切湍流流动中较k-ω模型和SST模型能够更好地模拟出湍流混合层中的流动特性，而经过可压缩修正后的CKDO模型则有更好的数值模拟性能，能够较准确地反映出可压缩自由剪切湍流混合层中典型的流动特性，且能便利植入其他模型来获得改进的计算精度，对于模拟其他复杂情况的可压缩湍流流动提供了一个全新的思路，有较好的工程应用价值。

[1]BIRCH S F, EGGERS J M. A critical review of the experimental data for developed free turbulent shear layers: NASA SP-321[R]. Washington, D.C.: NASA, 1972.

[2]GRUBER M R, MESSERSMITH N L, DUTTON J C. Three-dimensional velocity field in a compressible mixing layer[J]. AIAA Journal, 1993, 31(11): 2061-2067.

[3]WILCOX D C. Progress in hypersonic turbulence modeling: AIAA-1991-1785[R]. Reston: AIAA, 1991.

[4]WILCOX D C. A complete model of turbulence revisited: AIAA-1984-0176[R]. Reston: AIAA, 1984.

[5]WILCOX D C. Dilatation-dissipation corrections for advanced turbulence models[J]. AIAA Journal, 1992, 30(11): 2639-2646.

[6]WILCOX D C. Turbulence modeling for CFD[M]. California: DCW Industries, Inc., 1998: 180-183.

[7]MENTER F R. Improved two-equationk-omega turbulence models for aerodynamic flows: NASA TM-1992-103975[R]. Washington, D. C.: NASA, 1992.

[8]SARKAR S, ERLEBACHER G, HUSSAINI M Y, et al. The analysis and modeling of dilatational terms in compressible turbulence[J]. Journal of Fluid Mechanics, 1991, 227(3): 473-493.

[9]XU J L, ZHANG Y, BAI J Q. One-equation turbulence model based on extended Bradshaw assumption[J]. AIAA Journal, 2015, 53(6): 1433-1441.

[10]白俊强, 张扬, 徐晶磊, 等. 新型单方程湍流模型构造及其应用[J]. 航空学报, 2014, 35(7): 1804-1814.

BAI J Q, ZHANG Y, XU J L, et al. Construction and application of a new one-equation turbulence model[J]. Acta Aeronautica et Astronautica Sinica, 2014, 35(7): 1804-1814 (in Chinese).

[11]徐晶磊, 张扬, 白俊强, 等. 一个方程驱动转捩的湍动能单方程模型[C]//中国力学大会文集. 北京： 中国力学学会发， 2013: 142-149.

XU J L, ZHANG Y, BAI J Q, et al. A transition model based only on turbulence kinetic equation[C]//The Chinese Society of Theoretical and Applied Mechanics. Beijing: Chinese Society of Theoretical and Applied Mechanics, 2013: 142-149 (in Chinese).

[12]张扬, 徐晶磊, 白俊强, 等. 一种基于湍动能方程的转捩判定方法[J]. 力学学报, 2014, 46(1):160-164.

ZHANG Y, XU J L, BAI J Q, et al. A transition prediction method based on turbulence kinetic equation[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(1): 160-164 (in Chinese).

[13]BRADSHAW P, FERRISS D, ATWELL N. Calculation of boundary layer development using the turbulent energy equation[J]. Journal of Fluid Mechanics, 1967, 28(3): 593-616.

[14]HARSHA P T, LEE S C. Correlation between turbulent shear stress and turbulent kinetic energy[J]. AIAA Journal, 1970, 8(8): 1508-1510.

[15]文晓庆, 柳阳威, 方乐, 等. 提高k-ωSST模型对翼型失速特性的模拟能力[J]. 北京航空航天大学学报, 2013, 31(8): 1127-1132.

WEN X Q, LIU Y W, FANG L, et al. Improving the capability ofk-ωSST turubulence model for predicting stall characteristics of airfoil[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 31(8): 1127-1132(in Chinese).

[16]刘景源. SST湍流模型在高超声速绕流中的改进[J]. 航空学报, 2012, 33(12): 2192-2201.

LIU J Y. An improved SST turbulence model for hypersonic flows[J]. Acta Aeronautica et Astronautica Sinica, 2012, 33(12): 2192-2201 (in Chinese).

[17]徐晶磊, 阎超. 一个一方程Scale-Adaptive Simulation模型的构造[J]. 气体物理, 2010, 5(1): 79-82.

XU J L, YAN C. A one-equation scale-adaptive simulation model[J]. Physics of Gases, 2010, 5(1): 79-82 (in Chinese).

[18]WILCOX D C. Turbulence modeling for CFD[M]. California: DCW Industries, Inc., 2006: 243-261.

[19]GRUBER M R, MESSERSMITH N L, DUTTON J C. Three-dimensional velocity measurements in a turbulent compressible mixing layer[C]//28th Joint Propulsion Conference and Exhibit. Nashville: AIAA, SAE, ASME, and ASEE, 1992.

[20]GOEBEL S G, DUTTON J C, KRIER H, et al. Mean and turbulent velocity measurements of supersonic mixing layers[J]. Experiments in Fluids, 1990, 8(5): 263-272.

[21]POPE S B. Turbulent flows[M]. Cambridge: Cambridge University Press, 2000: 116-118.

[22]SETTLES G S, DODSON L J. Hypersonic turbulent boundary-layer and free shear database: NASA CR-1993-177610[R]. Washington, D.C.: NASA, 1993.

徐晶磊男， 博士， 讲师。主要研究方向： 湍流模式， 空气动力学。

Tel: 010-82317403

E-mail: xujl@buaa.edu.cn

宋友富男， 硕士研究生。主要研究方向： 计算流体力学， 湍流模型。

E-mail: songyoufu@buaa. edu. cn

张扬男， 博士研究生。主要研究方向： 设计空气动力学， 非定常空气动力学， 工程湍流模拟。

E-mail: vvip@nwpu.edu.cn

白俊强男， 博士， 教授， 博士生导师。主要研究方向： 工程湍流模拟， 流动控制。

Tel: 029-88492694

E-mail: junqiang@nwpu.edu.cn

Turbulence mixing length for compressible free shear flows

XU Jinglei1, *, SONG Youfu1, ZHANG Yang2, BAI Junqiang2

1. School of Energy and Power Engineering, Beihang University, Beijing100083, China 2. School of Aeronautics, Northwestern Polytechnical University, Xi’an710072, China

Seizing compressible flow variable density characteristics，a three-dimensional von Karman mixing length scale based on the effective vorticity has been constructed. This paper adopts a single-equation turbulence KDO (Kinetic Dependent Cnly) model which depends only on the turbulent kinetic energy equation, and introduces a new structure which replaces the old mixing length scale to obtain CKDO model. Then in order to verify its ability to describe compressible free shear turbulence, we select the compressible mixing layer of no wall bondage, large density gradient and strong compressibility effects as an example, whose convective Mach number is 0.8. The results show that KDO model has good control and simulation ability of mixing flow velocity distribution; compared with the original model and other compressible correction models, the velocity distribution, primary Reynolds shear stress and mixing layer thickness obtained with compressible correction model CKDO have a better fit with the experimental value. The results illustrate that the new mixing length has a good ability of characterization for compressible free shear turbulent mixing layer.

turbulence model; mixing layer; supersonic flow; compressibility; numerical simulation

2015-08-28； Revised： 2015-10-09； Accepted： 2015-11-04； Published online： 2015-12-0410:08

National Key Laboratory of Aircraft Engine Foundation of China (9140C410505150C41002)

. Tel.： 010-82317403E-mail: xujl@buaa.edu.cn

2015-08-28； 退修日期： 2015-10-09； 录用日期： 2015-11-04；

时间：2015-12-0410:08

www.cnki.net/kcms/detail/11.1929.V.20151204.1008.002.html

航空发动机气动热力国家科技重点实验室基金 (9140C410505150C41002)

.Tel.： 010-82317403E-mail: xujl@buaa.edu.cn

10.7527/S1000-6893.2015.0300

V211.3

A

1000-6893(2016)06-1841-10

引用格式： 徐晶磊， 宋友富， 张扬， 等． 用于可压缩自由剪切流动的湍流混合长度[J]． 航空学报, 2016, 37(6): 1841-1850. XU J L, SONG Y F, ZHANG Y, et al. Turbulence mixing length for compressible free shear flows[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6): 1841-1850.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

URL： www.cnki.net/kcms/detail/11.1929.V.20151204.1008.002.html