高斯平均引数大地主题解算程序设计★

田桂娥 谢 露 马广涛

(1.华北理工大学，河北 唐山 063000； 2.中铁十一局集团第一工程有限公司，湖北 襄阳 441104; 3.河北省制图院，河北 石家庄 050000)



·测量·

高斯平均引数大地主题解算程序设计★

田桂娥1谢 露2马广涛3

(1.华北理工大学，河北 唐山 063000； 2.中铁十一局集团第一工程有限公司，湖北 襄阳 441104; 3.河北省制图院，河北 石家庄 050000)

介绍了大地主题解算基本方法，以Visual Studio 2010作为开发平台，采用C#语言编写，设计实现了一套基于高斯平均引数的大地主题解算实用程序，指出该程序功能强大，实现了单点和批量大地主题解算，能方便的将计算结果保存在文本，且精度满足大地测量及相应工程的需求。

大地主题解算，高斯平均引数法，Visual Studio 2010，批量解算

0 引言

在天文大地测量中，为了获得点的大地坐标，需要在椭球面上进行控制点间的坐标解算。椭球面上两点间的大地坐标(大地经度、大地纬度)、大地线、大地方位角称为大地元素，已知一些大地元素，推求另一些大地元素，通常称为大地主题解算。大地主题解算包含大地主题正算和大地主题反算两种，已知椭球面上一点P1的大地坐标(L1，B1)，P1到P2点的大地线长度S及其大地方位角A12，计算P2点的大地坐标(L2，B2)和大地线长度S在P2点的反方位角A21，称为大地主题正解；反之，已知P1和P2点的大地坐标(L1，B1)和(L2，B2)，计算P1至P2的大地线长度S及其正反方位角A12和A21，称为大地主题反解。由于椭球计算的复杂性，带来大地主题解算的复杂性，有的需要进行迭代计算逐步趋近，给人工计算带来极大困难。随着计算机技术的飞速发展，计算机在大地主题解算上的应用也得到了快速的发展，迭代计算已经不再是难题，而且，可以根据精度的需要而自行确定迭代次数，极大的提高了计算效率。同时，随着大地主题解算在空间技术领域的广泛运用，大地主题解算已经成为一项重要的研究工作。

由于大地主题解算的目的和计算工具的不同，目前大地主题解算方法至少有70余种。根据解算方法的推导理论，这些解算方法大致可归纳为以下五类，即：1)以大地线在大地坐标系中的微分方程为基础，以高斯平均引数法为代表，这类方法仅适用于短距离大地主题解算；2)以白塞尔大地投影为基础，与距离长短无关，其衍生公式有镶嵌系数法，适用于任意长度大地主题解算；3)利用地图投影理论解算大地问题，计算原理和白塞尔类似，但是其受距离限制，因此只有在特殊情况下使用才有利；4)对大地微分方程进行数值积分的解法；5)依据大地线外的其他方程为基础。

本文在Visual Studio 2010的平台上，采用C#语言编写，以高斯平均引数法大地主题解算为基础，设计实现了一套大地主题解算实用程序，为大地测量人员提供方便。

1 大地主题解算常用解法

1.1 高斯平均引数法正算

(1)

为了使级数项数减少，收敛快，精度高，高斯平均引数公式将勒让德级数由在P1点展开改为在大地线长度中点M展开；其次，考虑到求定中点M的复杂性，将M点用大地线两端点平均纬度及平均方位角相对应的m点来代替，并借助迭代，顺利实现大地主题正解。高斯平均引数法正算公式具体如下：

其中，B为大地纬度；L为大地经度；A为大地方位角；Bm为P1和P2点平均纬度；Am为P1和P2的平均方位角，并有:

(2)

(3)

(4)

1.2 高斯平均引数法反算

已知经差ΔL，纬差ΔB及平均纬度Bm，求S，A12，A21，首先根据正算公式(1)，推导求出S·sinAm，S·cosAm，ΔA″具体推导见孔祥元等编写的“控制测量学(下册)”第三版，在此基础上求解Am，具体如下：

(5)

根据求得的Am，求解S，A12，A21:

(6)

应用上述公式时，应注意判断Am的象限。此套公式结构简单，收敛速度快，无需迭代。

2 算例与结果分析

本文以Visual Studio 2010作为开发平台，采用C#语言编写，以高斯平均引数为基础，可计算克拉索夫斯基椭球、1975国际75椭球、WGS84椭球、CGCS2000四个椭球下的大地主题正反算，程序界面清晰，容错性强，可实现单点和批量计算，同时可将计算结果保存为文本形式，简单方便。

本文大地主题正算中选取4个已知点(见表1)，已知数据D1，D2，D3，D4来源于参考文献[4]。表2给出了4个已知点高斯平均引数大地主题正算的结果及误差。从表2可以看到，4个已知点的大地经纬度和大地方位角解算真误差均在0.000 1″，最大的误差为D3点的大地经度之差ΔL2=0.000 8″，最小误差为0；以上所有点间大地线长度都在500 km以下，进一步验证了高斯平均引数法适用于短距离大地主题解算的条件。

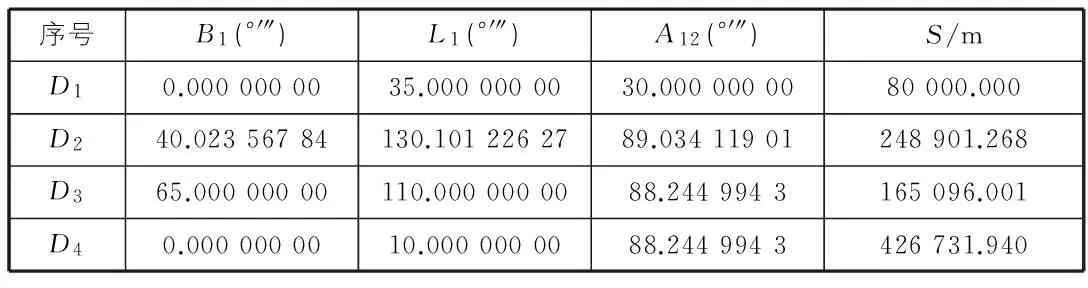
表1 大地主题解算正算已知数据

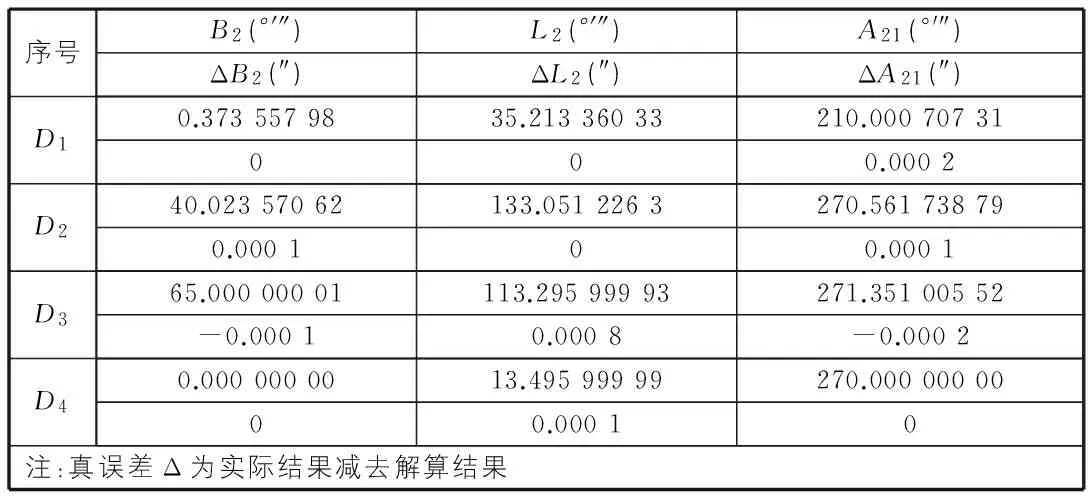
表2 高斯平均引数法大地主题解算正算结果

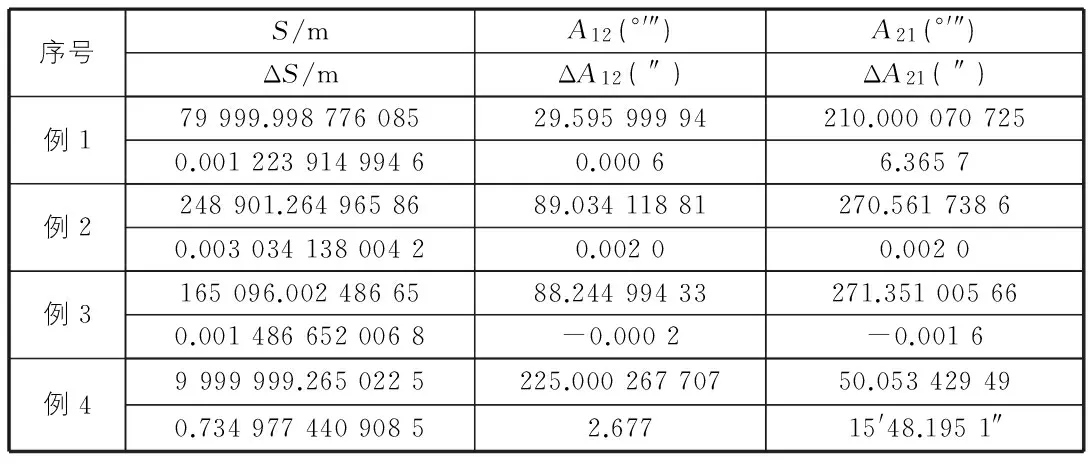
表3 高斯平均引数法大地主题解算反算结果

表3中选取了4套坐标实例，每套坐标中已知点间大地线长度范围为80 km～430 km不等。从表3中数据可以看到大地坐标正反方位角的计算真误差达到0.000 1″，距离真误差达到米级。在4个实例中，例4误差最大，无论距离、大地坐标方位角误差等均远超前3个例子的误差。经分析，例4中大地线长度为1 000 km，超过了高斯平均引数法解算的范围(500 km)，也就是可以说明，本程序高斯平均引数大地主题解算的精度达到距离0.001 m，角度0.000 1″，同时也验证了高斯平均引数大地主题解算适用于短距离的大地主题解算，解算精度与距离有关。

程序运行后，所有解算结果可以保存为报告输出到指定位置，报告中详细包含了大地主题解算的原始数据、解算结果、真误差、计算椭球以及椭球参数、迭代次数等，极大的方便了大地工作者及相关工作人员。

3 结语

本文在以高斯平均引数法为基础的大地主题解算程序，实现大地主题正反算精度达到角度0.000 1″、距离0.001 m，满足大地测量的要求。程序运行结果以报告形式输出，内容详细，清晰，为大地测量工作者带来极大方便。同时进一步验证了高斯平均引数法适用于短距离大地主题解算，大地线长度在500 km以内的大地主题解算均能达到较高精度。

[1] 周振宇，郭广礼，贾新果.大地主题解算方法综述[J].测绘科学，2007(4)：190-191.

[2] 徐晓晗，谢云开，李亚军.大地主题解算实用算法[J].科学技术与工程，2012(9)：2062-2068.

[3] 丁士俊，杨艳梅，史俊波，等.大地主题解算几种不同算法在计算中应注意的问题[J].黑龙江工程学院学报(自然科学版)，2013，27(3)：1-5.

[4] 孙祥元，郭际明.控制测量学(下册)[M].武汉：武汉大学出版社，2006.

[5] 尹文亭,徐昌荣.基于C#的嵌套系数法大地主题反解研究[J].江西理工大学学报,2013(1):55-58.

[6] 裴连磊.用C语言实现大地主题解算[J].价值工程,2013(20):235-236.

[7] 史国友,周晓明,贾传荧.贝塞尔大地主题正解的改进算法[J].大连海事大学学报,2008(1):15-19.

[8] 王爱生,徐 欢,张 棋,等.基于CGCS2000椭球的大地测量实用公式[J].导航定位学报,2015(3):105-109.

[9] 施一民,朱紫阳.新型大地坐标系中大地线的微分方程和微分式[J].同济大学学报(自然科学版),2007(1):108-111.

[10] 纪 兵,边少锋.大地主题问题的非迭代新解[J].测绘学报,2007(2):269-273.

[11] 张学廉.综合大地主题及其实用模型[J].武汉测绘科技大学学报,1987(1):59-69.

Program designing of geodetic theme solution of Gauss mid-lattitud method★

Tian Gui’e1Xie Lu2Ma Guangtao3

(1.NorthChinaUniversityofScienceandTechnology,Tangshan063000,China;(2.No.1EngineeringCo.,LtdofCR11BG,Xiangyang441104,China;

3.HebeiMappingInstitute,Shijiazhuang050000,China)

In this thesis, it introduces the geodetic solution basic method, and then design a program based on Gauss mid-lattitud method against geodetic solution utility. The program that with Visual Studio 2010 as a development platform, the C# language to write. The program has powerful function, realizes the single point and the bulk earth theme solution, and can be convenient to save the calculation results in the text, to meet the requirements of geodetic surveying and the corresponding engineering.

solution to geodetic problem, Gauss mid-lattitud method, Visual Studio 2010, batch calculation

1009-6825(2016)27-0192-02

2016-07-13

★:国家自然基金项目(项目编号：41574072)；华北理工大学教改项目(项目编号：Qz1432-10)；河北省测绘实验教学示范中心项目

田桂娥(1980- )，女，硕士，讲师； 马广涛(1983- )，男，工程师

TU198

A