去中心化且固定密文长度的基于属性加密方案

肖思煜 葛爱军,3 马传贵,2

1(数学工程与先进计算国家重点实验室(中国人民解放军信息工程大学) 郑州 450000)2(陆军航空兵学院 北京 101116)3(信息安全国家重点实验室(中国科学院信息工程研究所) 北京 100093) (siyuxiao32@163.com)



去中心化且固定密文长度的基于属性加密方案

肖思煜1葛爱军1,3马传贵1,2

1(数学工程与先进计算国家重点实验室(中国人民解放军信息工程大学) 郑州 450000)2(陆军航空兵学院 北京 101116)3(信息安全国家重点实验室(中国科学院信息工程研究所) 北京 100093) (siyuxiao32@163.com)

基于素数阶双线性群，提出了一种去中心化的基于属性加密方案，并在标准模型下证明了方案的安全性.该方案中含有一个中央机构(central authority, CA)和多个属性机构(attribute authority, AA)，其中中央机构负责生成与用户全局唯一身份标识绑定的随机值，并且不参与任何属性相关的操作，有效地抵抗了合谋攻击.每个属性机构负责互不相交的属性域并且相互独立，甚至不需要知道其他属性机构的存在.特别地，任何机构都不能独立解开密文.进一步，可以将该方案推广至多中央机构情形，中央机构之间亦相互独立，用户只需在其信任的任何一个中央机构注册即可，实现了真正意义上的“去中心化”.该方案中密文长度达到了固定值，同时解密运算只需要2个双线性对，在Charm架构下的仿真实验表明：该方案具有非常高的效率.

去中心化；多机构基于属性加密；密文数据访问控制；固定长度密文；抗合谋攻击

作为一种新型的公钥密码技术，基于属性加密体制[1]在对数据加密的同时，还可以基于用户属性对数据的解密权限进行细粒度的控制，很好地解决了密文机密性和访问控制灵活性的冲突，是云环境下基于密码学方法实现对数据对象访问控制的关键技术[2]，在安全云存储[3]、物联网隐私保护[4]以及社交网络访问[5]等领域都有着广泛的应用前景.

基于属性密码体制可看作是基于身份密码体制[6]的推广.在基于属性加密系统中，用户的身份标识被泛化为与其身份相关的一系列描述性的属性集合，如性别、年龄、职业、级别等，同时用户私钥以及密文都与属性相关联.加密者在加密数据的时候并不需要知道用户的公钥或者具体身份信息，只有满足访问策略的用户才能对密文成功解密.通过在密文或者私钥中嵌入访问策略的方法，基于属性加密体制提供了灵活的访问控制，并且相比基于身份加密体制的“一对一”通信模式，基于属性加密体制是一种“多对多”的通信模式：即一个密文可以被多个私钥解密，同时一个私钥也可以解密对应不同访问结构的密文.基于属性加密体制的这些特点，非常适合云计算等加解密方都不固定的应用场景，因此受到了广泛的关注，并成为当前密码理论及应用领域的研究热点[7].

需要指出的是，传统的基于属性加密系统都是单机构情形，即系统中只存在一个认证授权中心负责管理所有的属性，为每个用户分发相应的私钥，工作量巨大并且容易成为系统瓶颈.同时，该授权机构能够解密系统所有的密文，因此也需要求授权机构完全可信.针对此问题，Chase[8]最早研究了多机构的基于属性加密体制.多机构基于属性加密系统可以将单授权机构的信任和工作量分散到系统所有授权机构，有效减轻了单授权机构的负载，同时也符合分布式应用要求信任扩散的原则，在实际中应用更加广泛.

在多机构基于属性加密体制中，系统授权机构一般由一个中央机构(central authority, CA)和多个属性机构(attribute authority, AA)组成.用户从中央机构CA处获得与其身份相关的密钥，从属性机构AA处获得与其属性相关的密钥.为了保证解密算法的正确性，属性机构AA的秘密密钥一般是由中央机构CA根据系统主密钥计算生成，即中央机构CA具有非常强的解密权限，可解密系统所有密文.

为了避免使用中央机构CA带来的安全脆弱性问题，林煌等人[9]采用密钥分发和联合零秘密共享技术，最早提出了一种不需要中央机构的多属性机构基于属性加密体制.此外，Chase等人[10]在文献[8]基础上也构造了一个隐私性保护且无中央机构的多机构基于属性加密方案.但是这类方案要求所有属性机构必须在线并且通过交互方可建立系统，效率较低.

2011年，密码学家Lewko和Waters[11]提出了一种新型的称之为去中心化的基于属性加密体制(decentralized attribute-based encryption).中央机构在系统建立后即可退出，任何一个实体都可充当属性机构的角色，并且无需中央机构协助即可独立为用户分发相关属性密钥.特别地，在去中心化的基于属性密码系统中，属性机构相互之间是完全独立的，甚至不必知道其他属性机构的存在.

Lewko和Waters[11]提出的方案具有非常强的灵活性，能够支持任意单调访问结构，但是该方案及其改进方案[12]只能在随机预言模型(random oracle model, ROM)下可证明安全，即在安全性证明中需要把Hash函数假定为一个完全随机的预言机.而实际中的Hash函数与随机预言机的问答模式是有区别的，近年来也有学者指出某些在随机预言模型下可证明安全的方案在Hash函数实例化后并不安全[13]，因此，在不借助于随机预言机的标准模型下设计去中心化的多机构基于属性加密方案更有意义.国内外学者在这领域已有一些探索[14-18]，但是这些方案或者安全性证明不够严谨[14,16]，或者安全性存在缺陷[15]，不能抵抗合谋攻击[17-18].因此，如何在标准模型下构造可证明安全的去中心化的基于属性加密方案，这仍然是一个有待解决的公开问题.

为了减少对中央机构的信任，另外一个思路就是由刘振等人[19]提出的多中央机构和多属性机构的基于属性加密体制.系统中存在多个中央机构和多个属性机构，其中中央机构负责为用户分发身份相关的密钥，不参与任何属性相关的密钥分发；而属性机构可独立分发属性相关的密钥.系统中没有单个机构能够独立地解开任何密文，因此它可以有效防止中央机构作弊，该方案在标准模型下可证明安全，并且具有诸多良好的性质：支持任意单调访问结构、适应性安全等.针对该方案基于合数阶双线性群构造所导致的效率不高问题，李琦等人[20]基于素数阶双线性群给出了一个改进方案，具有更高的计算效率.需要指出的是，上述2个多机构基于属性加密方案中[19-20]，中央机构通过门限秘密共享的方式分享系统主密钥，因此用户需要与所有中央机构交互以生成其身份密钥.特别地，如果系统中只有一个中央机构，则该中央机构可独立解密所有密文.

受刘振等人的多机构基于属性加密方案[19]启发,本文在单机构基于属性加密方案[21]的基础上构造了一个标准模型下可证明安全的去中心化基于属性加密方案.方案中授权机构由一个中央机构CA和多个属性机构AA组成，其中CA负责系统的建立以及生成与用户身份相关的密钥.每个属性机构AA负责不同的属性域，相互独立甚至不需要知道其他属性机构的存在.任何实体只需要在CA注册并生成关于自己属性相关的参数即可加入系统并成为一个属性机构.即便中央机构也不能单独解密，这保证了系统中没有单个机构能够独立地解开任何密文.针对中央机构负责为所有用户分发身份相关密钥所带来的负载过重问题，在不影响安全性的前提下，我们方案很容易推广到多中央机构情形，实现了真正意义上的“去中心化”.

在不借助于随机预言机的标准模型下，我们证明了所构造方案的安全性.该方案能够支持灵活的与非门访问策略，在选择性安全模型下基于n-BDHE假设证明了方案具有选择明文攻击(chosen plaintext attacks, CPA)安全性.特别地，在我们的方案中，密文长度达到了常数级别，与用户属性个数、访问策略属性个数都无关，同时解密运算只需要2个双线性对运算，具有非常高的计算效率.本文最后，我们在Charm架构[22]下对方案进行了具体实现，分别考虑了在固定访问策略中属性个数而增加用户属性个数，以及固定用户属性个数而增加访问策略中属性个数这2种情况下，密钥生成、加密以及解密算法分别运行时间的变化，实验结果正如预期.

1 准备知识

1.1 双线性映射

设G和GT是2个阶为素数p的乘法循环群，g是G的生成元，如果一个映射e:G×G→GT同时满足3个性质：

1) 双线性性.对任意u,v∈p，有：e(gu,gv)=e(g,g)uv.

2) 非退化性.e(g,g)≠1.

3) 可计算性.对于任意的g,h∈G，存在多项式时间算法来计算e(g,h)的值.

则称这个映射是一个双线性映射.

1.2 困难性假设

本文基于属性加密方案的安全性依赖于n-BDHE假设，Boneh等人[23]证明了这个假设在一般群模型中是困难的，也即这个假设是合理的.下面给出这个复杂性假设的具体描述.

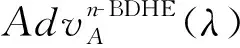
|Pr[A(g,gs,yg,α,n,e(gn+1,gs))=0]-

Pr[A(g,gs,yg,α,n,Z)=0]|，

其中,Z∈GT和s,α∈p均为随机选取.如果对于任意概率多项式时间的敌手(λ)对安全参数λ都是可忽略的，则称n-BDHE假设是成立的.

1.3 多机构基于属性加密

1.3.1 形式化定义

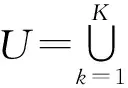
一个多机构基于属性加密方案包括4个阶段：1)系统建立阶段，包括生成系统全局参数、中央机构建立和属性机构建立；2)用户密钥生成阶段,包括身份密钥生成和属性密钥生成；3)加密阶段；4)解密阶段.特别地，当一个用户加入系统时，他首先访问中央机构获得身份相关的密钥，然后访问与其相关的属性机构获得该机构授权的属性密钥.具体而言，一个多机构基于属性加密方案应包括7个算法：

1)GlobalSetup(λ):系统建立算法.算法以安全参数λ为输入，输出系统公开参数GPK.

2)CASetup(GPK):中央机构建立算法.算法以系统公开参数GPK为输入，输出中央机构的主密钥CSK和公钥CPK，其中CPK只会被属性机构使用，在加解密算法中并不使用.

3)AASetup(GPK,Uk):属性机构建立算法.每个属性机构单独运行此算法来建立自己的公开参数和密钥.算法以系统公开参数GPK和序号为k的属性机构AAk管理的属性域Uk为输入，输出AAk的主密钥ASKk和公钥APKk.

4)CKeyGen(GPK,CSK,GID,S):身份密钥生成算法.由中央机构运行，算法以系统公开参数GPK、中央机构主密钥CSK、用户唯一身份标识GID和用户属性集合S为输入，输出用户的身份密钥SKGID,S.

5)AKeyGen(GPK,CPK,ASKk,SKGID,S,atti):属性密钥生成算法.当用户GID访问属性机构AAk请求属性atti的密钥时，AAk运行此算法.算法以系统公开参数GPK、中央机构公钥CPK、AAk主密钥ASKk、用户GID的身份密钥SKGID,S和属性atti∈S为输入，输出属性密钥SKGID,i.对于用户GID，我们用S表示他的属性集合，则他的解密密钥(decryptionkey)被定义为DKGID=(SKGID,S,{SKGID,i}atti∈S).

6)Encrypt(GPK,{APKk},M,W):加密算法.算法以系统公开参数GPK、相关属性机构的公钥{APKk}、消息M和一个访问策略W为输入，输出密文CTW.

7)Decrypt(GPK,CTW,DKGID):解密算法.算法以系统公开参数GPK、一个密文CTW和一个解密密钥DKGID为输入.令W表示密文CTW包含的访问策略，S表示解密密钥DKGID的属性集合，若S满足W，算法输出一个消息M，否则输出⊥表示解密失败.

1.3.2 安全模型

我们通过如下挑战者和攻击者之间的不可区分游戏来定义多机构基于属性加密方案的安全性.假设系统中只有一个中央机构且属性机构集合为Q={AA1,AA2,…,AAK}.

1) 系统建立.挑战者运行算法GlobalSetup,CASetup和AASetup(GPK,Uk)(k=1,2,…,K)，并且把GPK,CPK和{APKk|k=1,2,…,K}给攻击者.随后攻击者提交序号集合D⊂{1,2,…,K}来指定被其腐化的属性机构，挑战者把相应私钥{ASKk|k∈D}发送给攻击者.

2) 阶段1.攻击者可以自适应地向挑战者进行如下询问：

① 身份密钥询问.攻击者提交(GID,S)进行查询，挑战者返回相应的用户身份密钥SKGID,S.

② 属性密钥询问.攻击者提交(SKGID,S,atti∈S)进行查询，其中atti属于一个未被腐化的属性机构，挑战者生成相应的属性密钥SKGID,i给攻击者.

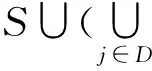
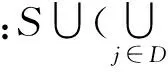
5) 猜测.攻击者输出对位b的猜测值b′∈{0,1}，当且仅当b=b′，敌手获得成功.

一个多机构基于属性加密方案被称为是适应性安全(adaptively secure)的，当且仅当任何概率多项式时间的敌手在上述不可区分游戏中成功的优势|Pr[b′=b]-12|都是可忽略的.

如果敌手在系统建立之前公布自己将要挑战的访问策略W，那么在这样的模型下证明的方案安全性被称为选择性安全(selectively secure).

2 具体方案

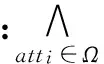
2.1 单中央机构情形

本节我们提出了一个单中央机构情形下的多机构基于属性加密方案，并且密文长度达到了常数级别，具体如下：

1)GlobalSetup(λ):系统建立算法.此算法由一个只参与系统建立阶段的可信第三方来运行.输入安全参数λ，生成一个p阶(p>2λ)双线性群(p,G,GT,e,g)并且选择一个存在性不可伪造的签名方案Σsign=(KeyGen,Sign,Verify)，输出系统公开参数GPK=(p,G,GT,e,g,Σsign).

2)CASetup(GPK):中央机构建立算法.中央机构运行Σsign中的KeyGen算法得到签名密钥对(Signkey,Verifykey)，其中签名私钥CSK=Signkey保密，CPK=Verifykey公开.

3)AASetup(GPK,Uk):属性机构建立算法.对于每个atti∈Uk，AAk随机选择ri∈p,ui∈G，计算Ri=g-ri以及Ti=e(ui,g)，然后公布公钥APKk={Ri,Ti|atti∈Uk}，并设定它的主密钥ASKk={ri,ui|atti∈Uk}.

4)CKeyGen(GPK,CSK,GID,S):身份密钥生成算法.用户GID将自己的全局唯一身份标识以及属性集合S发送给中央机构CA，CA随机选择V∈G，将SKGID,S=(GID,S,V,Sign(Signkey,GID‖S‖V))返回给用户.

5)AKeyGen(GPK,CPK,ASKk,SKGID,S,atti):属性密钥生成算法.当用户提交SKGID,S以及属性atti给AAk申请属性密钥时，AAk首先将SKGID,S进行拆分，并且验证签名Sign(Signkey,GID‖S‖V)的合法性，若验证成功且atti∈S成立，则计算并返回SKGID,i=uiVri给用户.用户GID的解密密钥定义为DKGID=(SKGID,S,{SKGID,i}atti∈S).

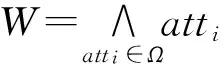
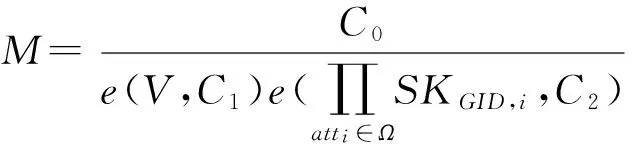
2.1.1 正确性分析

正确性验证如下：

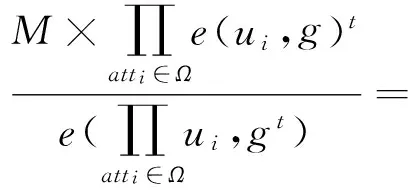
故上述方案是满足正确性的.

2.1.2 安全性分析

定理1. 假定签名方案Σsign在标准模型下是存在性不可伪造的，基于n-BDHE困难问题假设，我们构造的多机构基于属性加密方案对于选择性敌手是安全的.

证明. 本文为实现多机构的基于属性加密，将密钥生成算法中随机值V∈G的选择交由中央机构CA来负责，并将其与用户的全局唯一标识GID和属性集合S进行绑定，这样可以有效防止恶意用户之间的合谋攻击;否则，拥有不同属性的用户A和B之间可以通过共享同一个V来获得自己权限之外的信息.若方案中的签名算法满足存在性不可伪造，则用户不可能生成一个有效的签名，所以即使想共享同一个V，也通不过属性机构AAs的验证.

假设挑战者S输入一个在双线性群(p,G,GT,e,g)上的n-BDHE实例(g,h,yg,α,n,T)，他可以通过下列步骤来模拟不可区分游戏.

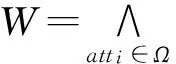
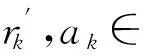
(Ri*,Ti*)=(g-ri*,e(ui*,g))=

对于i∈{j|attj∈Ω*{atti*}}，计算:

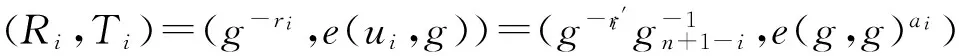
否则，计算:

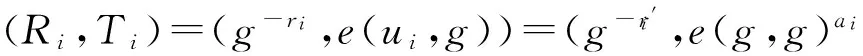
挑战者再选取存在性不可伪造的签名算法Σsign=(KeyGen,Sign,Verify)，并且生成签名密钥对(Signkey,Verifykey)，将{(Ri,Ti)|atti∈U}， {(ri,ui)|atti∈UU1}以及(p,G,GT,e,g,Σsign,Verifykey)发送给敌手A.

2) 阶段1.敌手可以自适应地向挑战者进行任意密钥问询：

① 身份密钥问询.敌手首先将全局唯一标识GID和属性集合S发送给挑战者，其中Ω*⊄S，所以必然存在atti′∈Ω*S.挑战者S选取随机的v∈p，计算V=gi′gv，将δ=(GID,S,V,Sign(Signkey,GID‖S‖V))发送给敌手.

② 属性密钥问询.敌手将(δ,atti)提交给挑战者，其中atti∈S由属性机构AA1控制.挑战者首先拆分δ并验证签名的合法性，然后按如下规则进行密钥回复.

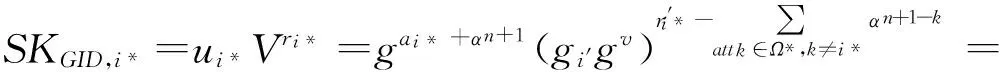
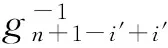
若i≠i*，计算:

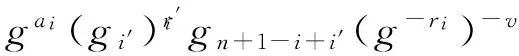
这里我们假定i*≠i′，如果i*=i′，就只需要按照第2种方式计算密钥.将SKGID,i返回给敌手.

3) 挑战.在某个时刻，敌手A提交给挑战者2个等长消息M0,M1，挑战者随机选择比特b∈{0,1}，计算

C0=MbTe(g,h)aΩ，C1=h-rΩ，C2=h，

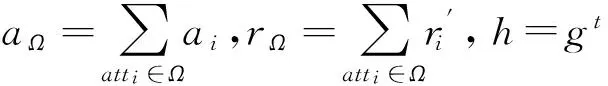
Mbe(gn+1,h)e(g,h)aΩ，

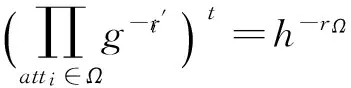
当T=e(gn+1,h)时，CT=(C0,C1,C2)是明文Mb的合法密文.否则，在敌手眼里CT是一个随机消息的对应密文.

4) 阶段2.同阶段1.

5) 猜测.敌手A输出对位b的猜测值b′，如果b′=b，则挑战者S输出0；否则，输出1.

如果敌手能以ε的优势攻破上述加密方案，则挑战者能以同样ε的优势解决n-BDHE问题.

证毕.

值得注意的是，在我们的方案中，敌手每次问询GID的身份密钥，挑战者都选择一个随机值作为回答，而属性密钥是在身份密钥的基础生成的，因此只要每一个S都不能满足挑战访问策略，同一个GID就可以询问多个不同属性集合S的密钥.

2.2 多中央机构的情形

为减轻一个中央机构为所有用户生成身份密钥带来的负载过重的问题，我们可以将上述方案拓展到多中央机构的情形，做到真正意义上的去中心化.

1)GlobalSetup(λ):系统建立算法.与单中央机构情形相同.

2)CASetup(GPK,j):中央机构建立算法.第j个中央机构CAj单独运行Σsign中的KeyGen算法得到签名密钥对(Signkeyj,Verifykeyj)，其中CSKj=Signkeyj保密，CPKj=Verifykeyj公开.

3)AASetup(GPK,Uk):属性机构建立算法.与单中央机构情形相同.

4)CKeyGen(GPK,CSKj,GID,S):身份密钥生成算法.用户将自己的全局唯一身份标识GID以及属性集合S发送给任意一个中央机构CAj申请身份密钥，CAj随机选择V∈G，计算SKGID,S,j=(GID,S,V,j,Sign(Signkeyj,GID‖S‖V‖j))并将其返回给用户.

5)AKeyGen(GPK,{CPKj},ASKk,SKGID,S,j,atti):属性密钥生成算法.用户将SKGID,S,j以及属性atti发送给相应的AAk申请属性密钥，AAk首先将δGID,S,j进行拆分，并且验证签名Sign(Signkeyj,GID‖S‖V‖j)的合法性，若验证成功且atti∈S成立，则计算并返回SKGID,i=uiVri给用户.

6) 加解密算法与单中央机构情形相同.

定理2. 假定签名方案Σsign在标准模型下是存在性不可伪造的，那么基于n-BDHE困难问题假设，上述多中央机构情形下的方案也是选择性安全的.

证明. 方案中引入多个中央机构只是为了缓解单个中央机构运算量过大的问题，并不影响方案的安全性，即多个中央机构的安全性证明与单中央机构情形基本相同，这里就不再赘述.

证毕.

3 实验结果与分析

表1将本文多机构基于属性加密方案和相关方案在效率和安全模型方面进行了详细的比较，其中l是指表示某个单调布尔函数的线性秘密共享(linear secret sharing scheme, LSSS)矩阵的行数，S代表密钥属性集合，D和K分别代表CA和AA的个数，|I|是指LSSS矩阵用于解密的行数.

Table 1 Efficiency Comparisons of Different Multi-Authority ABE

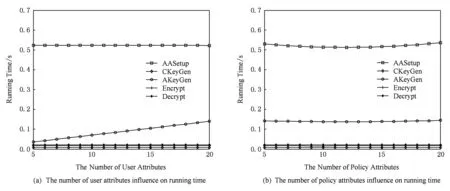
Fig. 1 The number of user attributes and policy attributes influence on running time.图1 用户属性和策略属性数目对方案运行时间的影响

与其他2个方案相比，本文的方案实现了固定密文长度与固定数目的双线性对运算，在计算和存储上有着较大的优势.尽管只能支持简单的与非门访问策略，但是在一般场景下，这种策略已经足够满足实际需求.

为验证本文方案在实际部署中的可用性，我们在Charm架构下对其进行了具体实现.注意到GlobalSetup中的签名方案Σsign与加解密算法是互不影响的，我们主要考虑加解密算法.

在图1(a)中，我们考察了用户属性个数对方案中各个算法运行时间的影响.在实验中，我们令整个系统中属性总数N=20，访问策略中属性个数N1=4，用户属性个数由5变化至20.可以看出，只有属性密钥生成算法AKeyGen的平均运行时间随着用户属性个数的增加线性增长，其余算法包括加解密时间与用户属性个数无关.

在图1(b)中，我们考察了策略属性个数对方案中各个算法运行时间的影响.在该实验中，我们令整个系统中属性总数N=20，用户属性个数N2=20，策略属性个数由5变化至20.从图1中可以看出，加密时间与所涉及的策略属性数目无关.并且加密算法中只涉及到群中的指数运算，速度较快，平均时间大约是0.016 s.解密算法中涉及到2个对运算，但是不管策略属性数目如何增长，其运行时间基本也在0.02 s左右，变化不大.

4 结束语

在去中心化的多机构基于属性加密体制中，不同的属性域由不同的属性机构进行管理，每个属性机构都独立运作，并且没有机构能够独立解开任何密文.将单授权机构的信任和工作量分散到系统所有授权机构，有效减轻了传统的基于属性加密体制中单授权机构的负载，同时也契合网络结构去中心化的趋势，在实际中有着更加广泛的应用前景.

本文基于素数阶双线性群构造的去中心化基于属性加密方案，在标准模型下基于n-BDHE假设证明了方案具有选择性安全.特别地，该方案中密文长度达到了常数级别，与用户属性个数、访问策略属性个数都无关，同时解密运算只需要2个双线性对，在Charm架构下的仿真实验表明该方案具有非常高的效率.本文方案不足之处在于表达力有限，只能支持简单的与非门访问策略，即通过牺牲访问结构的表达性来达到提高方案效率的目的.如何在标准模型下构造表达力更强的或者适应性安全的去中心化基于属性加密方案，这是当前研究的公开难题，也是下一步我们要继续研究的问题.

[1]Sahai A, Waters B. Fuzzy identity-based encryption[G] //LNCS 3494: Proc of Int Conf on Theory and Applications of Cryptographic Techniques. Berlin: Springer, 2005: 457-473

[2]Feng Dengguo, Zhang Min, Zhang Yan, et al. Study on cloud computing security[J]. Journal of Software, 2011, 22(1): 71-83 (in Chinese)(冯登国, 张敏, 张妍, 等. 云计算安全研究[J]. 软件学报, 2011, 22(1): 71-83)

[3]Fu Yingxun, Luo Shengmei, Shu Jiwu. Survey of secure cloud storage system and key technologies[J]. Journal of Computer Research and Development, 2013, 50(1): 136-145 (in Chinese)(傅颖勋, 罗圣美, 舒继武. 安全云存储系统与关键技术综述[J]. 计算机研究与发展, 2013, 50(1): 136-145)

[4]Dong Xiaolei. Advances of privacy preservation in Internet of things[J]. Journal of Computer Research and Development, 2015, 52(10): 2341-2352 (in Chinese)(董晓蕾. 物联网隐私保护研究进展[J]. 计算机研究与发展, 2015, 52(10): 2341-2352)

[5]Lü Zhiquan, Hong Cheng, Zhang Min, et al. Privacy-preserving scheme for social networks[J]. Journal of Communications, 2014, 35(8): 23-32 (in Chinese)(吕志泉, 洪澄, 张敏, 等. 面向社交网络的隐私保护方案[J]. 通信学报, 2014, 35(8): 23-32)

[6]Shamir A. Identity-based cryptosystems and signature schemes[G] //LNCS 196: Advances in Cryptology. Berlin: Springer, 1985: 47-53

[7]Su Jinshu, Cao Dan, Wang Xiaofeng, et al. Attribute-based encryption schemes[J]. Journal of Software, 2011, 22(6): 1299-1315 (in Chinese)(苏金树, 曹丹, 王小峰, 等. 属性基加密机制[J]. 软件学报, 2011, 22(6): 1299-1315)

[8]Chase M. Multi-authority attribute based encryption[C] //Proc of the 4th Theory of Cryptography Conf (TCC 2007). Berlin: Springer, 2007: 515-534

[9]Lin Huang, Cao Zhenfu, Liang Xiaohui, et al. Secure threshold multi authority attribute based encryption without a central authority[G] //LNCS 5365: Proc of the 9th Int Conf on Cryptology in India (INDOCRYPT 2008). Berlin: Springer, 2008: 426-436

[10]Chase M, Chow S. Improving privacy and security in multi-authority attribute-based encryption[C] //Proc of the 16th ACM Conf on Computer and Communications Security. New York: ACM, 2009: 121-130

[11]Lewko A, Waters B. Decentralizing attribute-based encryption[G] //LNCS 6632: Advances in Cryptology (EUROCRYPT). Berlin: Springer, 2011: 568-588

[12]Okamoto T, Takashima K. Decentralized attribute-based signature[G] //LNCS 7778: Proc of Public Key Cryptology (PKC). Berlin: Springer, 2013: 125-142

[13]Canetti R, Goldreich O, Halevi S. The random oracle methodology, revisited[C] //Proc of ACM Annual Symp on Theory of Computing (STOC). New York: ACM, 1998: 209-218

[14]Han Jinguang, Susilo W, Mu Yi, et al. Privacy-preserving decentralized key-policy attribute-based encryption[J]. IEEE Trans on Parallel and Distributed Systems, 2012, 23(11): 2150-2162

[15]Han Jinguang, Susilo W, Mu Yi, et al. Improving privacy and security in decentralized ciphertext-policy attribute-based encryption[J]. IEEE Trans on Information Forensics and Security, 2015, 10(3): 665-678

[16]Yogachandran R. User collusion avoidance scheme for privacy-preserving decentralized key-policy attribute-based encryption-full version[EB/OL]. [2016-06-20]. http://120.52.73.76/arxiv.org/pdf/1602.01261v1.pdf

[17]Ge Aijun, Zhang Jiang, Zhang Rui, et al. Security analysis of a privacy-preserving decentralized key-policy attribute-based encryption scheme[J]. IEEE Trans on Parallel and Distributed Systems, 2013, 24(11): 2319-2321

[18]Wang Minqian, Zhang Zhenfeng, Chen Cheng. Security analysis of a privacy-preserving decentralized ciphertext-policy attribute-based encryption scheme[J]. Concurrency and Computation: Practice and Experience, 2016, 28(4): 1237-1245

[19]Liu Zhen, Cao Zhenfu, Huang Qiong, et al. Fully secure multi-authority ciphertext-policy attribute-based encryption without random oracles[G] //LNCS 6879: Proc of Computer Security (ESORICS). Berlin: Springer, 2011: 278-297

[20]Li Qi, Ma Jianfeng, Xiong Jinbo, et al. An adaptively secure multi-authority ciphertext-policy ABE scheme on prime order groups [J]. Acta Electronica Sinica, 2014, 42(4): 696-702 (in Chinese)(李琦, 马建峰, 熊金波, 等.一种素数阶群上构造的自适应安全的多授权机构CP-ABE方案[J]. 电子学报, 2014, 42(4): 696-702)

[21]Chen Cheng, Zhang Zhenfeng, Feng Dengguo. Efficient ciphertext policy attribute-based encryption with constant-size ciphertext and constant computation-cost[C] //Proc of the 5th Int Conf on Provable Security (ProvSec 2011). Berlin: Springer, 2011: 84-101

[22]Akinyele J A, Garman C, Miers I, et al. Charm: A framework for rapidly prototyping cryptosystems[J]. Journal of Cryptographic Engineering, 2013, 3(2): 111-128

[23]Boneh D, Boyen X, Goh E. Hierarchical identity based encryption with constant size ciphertext[G] //LNCS 3494: Advances in Cryptology (EUROCRYPT). Berlin: Springer, 2005: 440-456

Xiao Siyu, born in 1993. Master candidate. Her main research interests include public key encryption.

Ge Aijun, born in 1985. PhD. His main research interests include public key encryption and digital signatures.

Ma Chuangui, born in 1962. Professor and PhD supervisor. His main research interests include network and information security(chuaguima@sina.com).

Decentralized Attribute-Based Encryption Scheme with Constant-Size Ciphertexts

Xiao Siyu1, Ge Aijun1,3, and Ma Chuangui1,2

1(StateKeyLaboratoryofMathematicalEngineeringandAdvancedComputing(PLAInformationEngineeringUniversity),Zhengzhou450000)2(ArmyAviationInstitute,Beijing101116)3(StateKeyLaboratoryofInformationSecurity(InstituteofInformationEngineering,ChineseAcademyofSciences),Beijing100093)

Based on prime-order bilinear groups, we propose a decentralized multi-authority attribute-based encryption scheme which is proven to be secure in the standard model. Firstly, we construct an attribute-based encryption system with a central authority (CA) and multiple attribute authorities (AAs), where CA is responsible for generating a random value associated with each user’s unique global identifier (GID), and does not participate in any operation related to users’ attributes. Different users will get different random values, thus they cannot obtain any information beyond authority even through collusion. Every attribute authority is responsible for different attributes domain and they are independent of each other. It’s even not necessary to know the existence of each other in the system. In particular, there is no authority that can decrypt a ciphertext alone. Secondly, this scheme can be extended to a decentralized attribute-based encryption with multiple CAs setting, where every CA is also independent of each other, and each user can issue his private key from only one CA. Bringing it into practice under the Charm infrastructure, the results show that the decentralized attribute based encryption schemes are very efficient, whose ciphertexts are of constant size, i.e., regardless of the number of underlying attributes of access control policy or users.

decentralized; multi-authority attribute-based encryption; ciphertext access control; constant-size ciphertext; collusion resistant

2016-06-16；

2016-08-17

国家自然科学基金项目(61309016,61379150,61502529)；信息安全国家重点实验室开放课题(2016-MS-15)

葛爱军(geaijun@163.com)

TP309

This work was supported by the National Natural Science Foundation of China (61309016, 61379150, 61502529) and the Open Foundation of the Sate Key Laboratory of Information Security (2016-MS-15).