一道数列客观题的多角度探究

◇　陕西　雷文军

(作者单位：陕西省丹凤中学)



一道数列客观题的多角度探究

◇陕西雷文军

给出递推关系求数列通项公式问题,能有效考查同学们对所给关系分析、转化能力,因此备受命题人关注.解此类问题的关键是把握递推关系的结构特征、善于发现隐含的规律、熟练相关问题的通性通法．下面引例1说明．

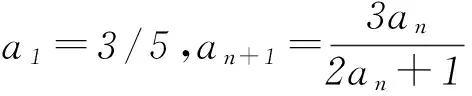
根据题中条件采用倒数法是一种常见解法:

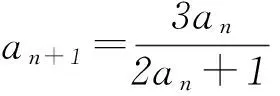
那么例1是否可以利用此方法求解呢?

一方面,分式的分子不是1项,而是2项的差,另一方面,等式展开后也不出现an+1an=can+1+dan的形式,不能用倒数法.

1　小题小做,猜想归纳

解法1利用已知数列{an}的递推公式求出数列的前几项,然后归纳猜想出数列的规律、特点.

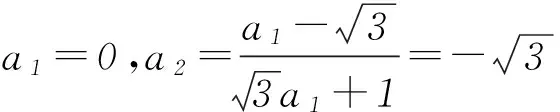
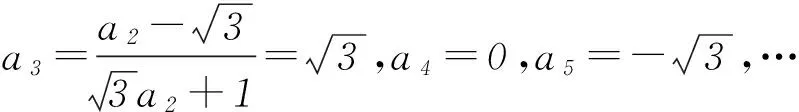
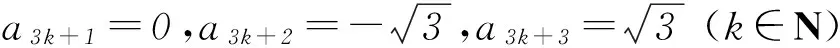
2　探究通法,夯实双基

解法2利用周期函数的定义,严格地推导出数列的最小正周期.

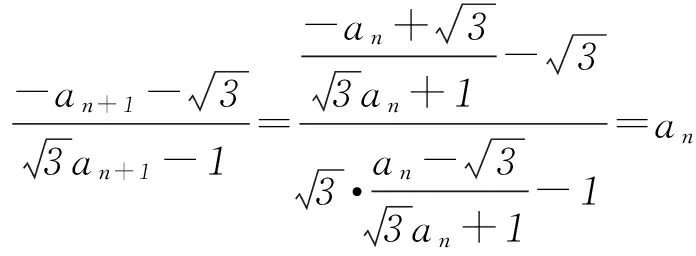
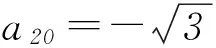
3　奇思妙想 发散思维

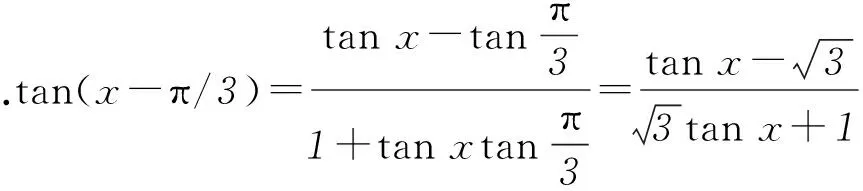
4　严谨思维 落实能力

通过大胆的联想实现了对问题的解答,但是联想只是停留在列举实例上,未免不够严谨.如果是一道解答题,如何借助三角函数方法严格推理呢?

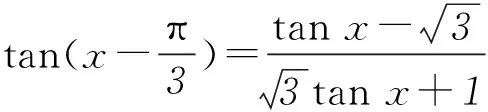
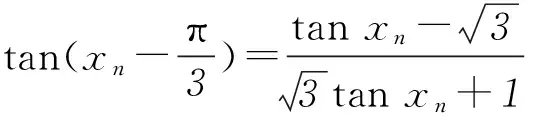
设an=tanxn,结合条件中的递推公式,得an+1=tan(xn-π/3),可见其中正切角构成的数列{xn}是公差为-π/3的等差数列．

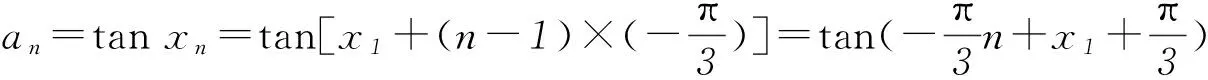
综上,对一道给出递推关系求通项问题的多角度探究,将其巧妙转化为我们所熟悉的特殊数列问题,从而使问题迎刃而解．另外,使用上述方法解题时,常可降低思维强度,简化推理和运算过程,具有直观、简捷、明快的特点．解题中要准确选用．

(作者单位：陕西省丹凤中学)