金价对蛇屋山金矿最优开采路径影响研究

王庆新， 熊 艳， 朱本杰

(1.湖北省地质局第四地质大队,湖北 咸宁 437100;2.中国地质大学 经济管理学院， 湖北 武汉 430074)



金价对蛇屋山金矿最优开采路径影响研究

王庆新1， 熊 艳2， 朱本杰1

(1.湖北省地质局第四地质大队,湖北 咸宁 437100;2.中国地质大学 经济管理学院， 湖北 武汉 430074)

蛇屋山金矿亟需以动态和可持续发展的策略应对矿产资源量的不断消耗及国际金价的持续大幅波动。依据可耗竭资源理论，以矿山利润最大化为目标，建立蛇屋山开采路径研究的动态模型，通过分析确定模型中的各参数，对蛇屋山金矿的开采路径进行优化。并模拟分析不同价格下蛇屋山金矿的开采路径，从时间维度确定矿山年开采资源配置路径，进而从空间维度确定了不同区块的配置路径，由此确定出不同块段资源开采量，使金矿的开采达到最优。研究结果表明了该模型的有效性，模型可以得出矿山空白区资源的最优开采路径区块开发顺序，并可以预测随着资源市场价格的变动，矿山的经济可采储量，从而实现可耗竭资源合理有效的开发利用。

可耗竭资源；动态模型；最优开采；开采路径

黄金是一种特殊商品且有可耗竭性，是各国外汇储备的重要组成部分和十分重要的金融资产。2008年金融危机以来，随着西方国家经济的复苏，以美元为主的货币逐渐走强，黄金价格在2013年开始进入不断下跌阶段，黄金市场风险逐步增加。黄金企业在矿山开发过程中面临着黄金价格波动和黄金资源有限双重约束。一方面，黄金价格波动既对企业运营产生冲击又带来套利空间，企业需要在矿山开发利用过程中依据价格波动来调整生产，降低价格经营风险，提高盈利能力；另一方面，金矿储量随着开发进程不断耗竭，这需要对矿山进行可持续开发利用。上述两个方面均需要企业在金矿开发过程中确定合理开发规模和开发时序，找到金矿资源的最优开采路径，提升企业应对市场风险的能力。因此，研究不同黄金价格下金矿最优开采路径具有重要的现实意义。

可耗竭资源理论是1931年由Hotellin提出的，他利用经典变分法研究可耗竭资源的跨期配置问题，提出了最优开采路径的“Hotelling规则”[1]。Herfindahl研究了关于资源开采顺序问题，认为在局部均衡前提下，资源应按照开采成本由低到高的顺序开采[2]。Tietenberg提出资源“跨期”的概念，构建了资源跨期有效配置模型[3]。这些理论在国内得到了诸多应用与发展，魏晓平建立了矿产资源价值动态模型，推出了矿产资源的最佳耗竭速度和最佳寿命期[4]。杨海生等通过一个连续时间的随机动态规划模型,探讨了市场需求、资源存量的不确定性以及勘探活动对矿产资源价格和开采速度的影响，并给出了随机条件下Hotelling法则的表达形式[5]。葛世龙等通过对回采率的调整方法进行分析，确定了矿产资源的有效可采储量，然后基于最优控制理论建立了可耗竭资源最优开采模型，确定了资源最优开采路径、影子价格和耗竭时间[6]。葛世龙等在技术出现时间不确定的基础上，分析资源开采成本与开采量相关以及有存货情形,利用动态规划思想处理了技术出现时间不确定,构建了动态优化模型,得到相应地HJB方程和最优开采路径[7]。胡静峰基于最优控制理论，建立石油耗竭期内的最优消耗效率模型[8]。

尽管上述文献为本文的理论研究和建模工作提供了丰富的借鉴，然而大多文献往往将矿山作为一个整体进行研究，仅将最优开采规模和开采时间视为最优路径，并没有将各时间节点上的最优开采量在矿山内部各区块进行最优分配。在矿山不同区块之间，由于储量不同和品位不同往往导致不同的开发成本，影响到最优产量在各区块的最优配置，进而影响矿山最优开采路径。而将最优产量在各区块进行最优配置矿山应对黄金价格波动的时间维度和空间维度上的有效响应。基于此，本文引入可耗竭模型、最优控制理论和动态规划理论，建立金矿最优开采配置路径模型，分析研究不同金价对金矿最优开采配置路径影响，为金矿企业应对价格风险提供理论借鉴和科学决策依据。

1 矿山最优开采配置路径模型

本研究假设矿山资源在[0,T]间隔期内是被连续开采，考虑时间变量是离散的，为了使模型简便，并能反映问题的实质，设某金矿资源的开采寿命期为T年，问题可分为相互联系的T个阶段，即(t=0,1,2,…，T-1)；设Pt为第t年矿产资源的市场价格，为外生变量；Xt为第t年矿产资源的开采规模，为决策变量；C(i,Xt)为第t年矿产资源边际开采成本，与矿产所在区块i以及开采时间t相关，其中i表示不同区块，i=0,1,2,…，N-1，(t=0,1,2,…，T-1)。

1.1 目标函数

在剩余生命周期内，矿产资源开采的总效益为：

(1)

式中：e-rt表示贴现系数；r为贴现率。矿产资源的开采目标是使开采价值达到最大,即:

(2)

1.2 约束条件

由于矿产资源的可耗竭性与不可再生,所以资源储量在开采期内是递减的,其满足

(3)

式中：Qt为第t年矿产资源的剩余矿石量，状态变量；Qt+1-Qt=-Xt是一组差分方程，给出了状态t到状态t+1转移规律，即在探明储量不变的情况下，连续两年剩余储量之差为当年的开采量，S(0)为初始储量，S(T)为期末T时刻储量。

以上就是矿产资源最优开采规模的跨期优化模型,即矿山最优开采配置路径模型。该模型考虑了贴现率的动态变化，以及技术进步对总开采成本的影响，描述了矿产资源开采规模和开采成本之间的动态关系。

1.3 模型求解

矿山最优开采配置路径模型是一个有T+1个约束条件的极值问题,将其转化为无约束的 Lagrange 极值问题:

(4)

为了推出(4)式的极值条件，引入Hamilton函数,令:

H=H(Xt,Qt,λt+1,t)=PtXt-C(i,Xt)-C0-e-rλt+1Xt

(5)

将(5)式代入(4)式有：

(6)

则(6)式取极值的必要条件为：

(t=0,1,2,……，T-1)

(7)

由上述必要条件可进一步得出(6)式取得最优解的条件：

(t=0,1,2,……，T-1)

(8)

将(8)中的后两个式子代入第一个式子整理可得：

Pt-C′(i,Xt)-ertλ0=0 (t=0,1,2,…，T-1)

(9)

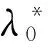
2 模型参数确定

将可耗竭资源理论结合蛇屋山金矿的开采成本、技术及资源禀赋等现状，确定出模型中的各个参数，对蛇屋山进行实证研究。贴现率r应当既反映货币的时间价值，又反映与项目有关的风险。适当的贴现率是由资本市场决定的，与该行业的总体市场收益率有关。关于贴现率的确定方法目前已较为成熟，故本文不做重点论述，结合当前我国矿产资源工业的发展状况及未来发展趋势，国家利率行情及相关参考文献的讨论，取其值为r=0.05；本研究结合矿山开采实际情况，将现有可开采金矿资源的开采寿命T确定为5年。地质因素会直接影响开采区的设计及金矿资源的工业品位，导致品位特征在一定区域内基本相似；地理位置、地上拆迁区分布会影响块段开采的转移范围。结合拆迁区分布以及块段品位分布，将148个块段综合划分为A、B、C、D、E、F等6个区块(图1)。

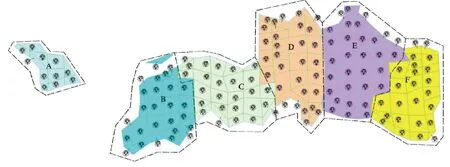
图1 蛇屋山区块划分

3 不同价格下金矿最优开采路径模拟

在上述模型构建、参数设置的基础上，模拟不同价格情况下金矿开采轨迹。考虑到目前金矿价格主要在250元/g波动，主要分析3种金矿价格下不同块段金矿开采路径：现有价格250元/g保持不变时的开采路径、现有价格每年增长5元/g时的开路径、现有价格每年增长15元/g时的开采路径。

3.1 现有价格250元/g保持不变时的开采路径

当现有价格250元/g保持不变时，仅有区块A及区块D达到最低工业品位，即需要在矿山净效益最大化目标下，在耗竭时间T内配置区块A及区块D各块段每年开采量。若价格保持250元/g不变，矿山可实现3年技术经济可采矿石量(图2)。第一年，区块A技术经济可采矿石量完全开采，区块D技术经济可采矿石量部分开采；第二年，区块D技术经济可采矿石量部分开采；第三年，区块D技术经济可采矿石量完全开采。具体产量和利润如表1所示。

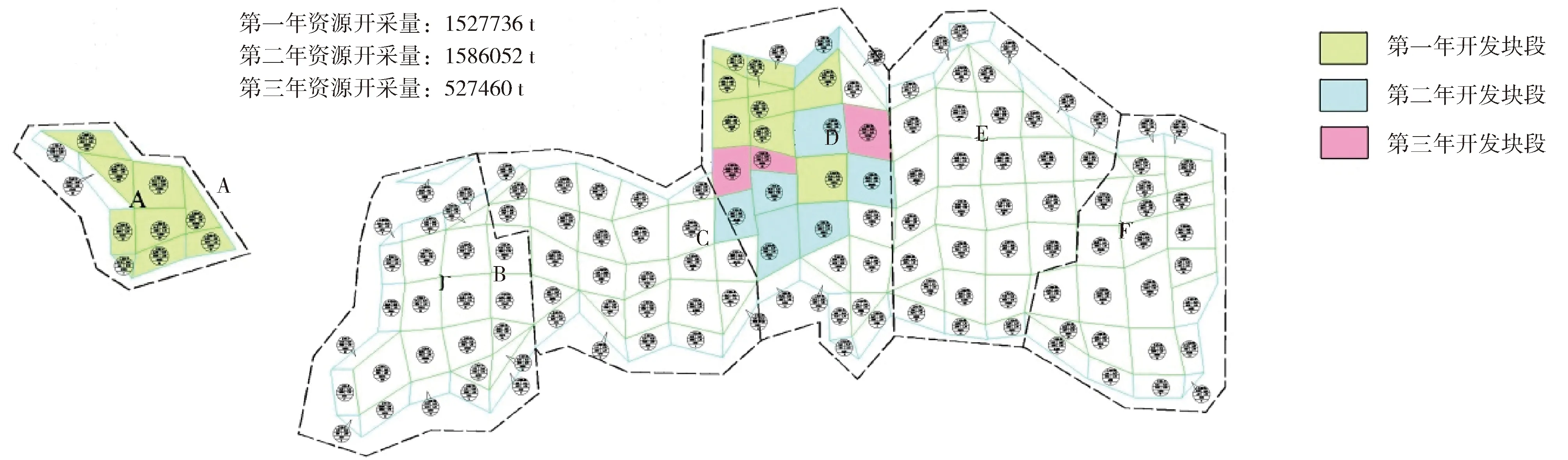
图2 金价250元/g下金矿开采量路径

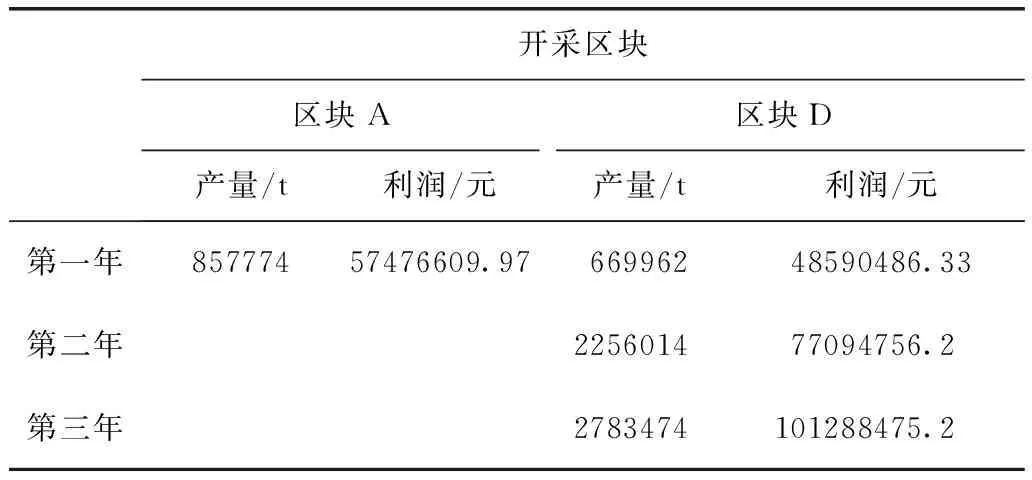
开采区块区块A区块D产量/t利润/元产量/t利润/元第一年85777457476609.9766996248590486.33第二年225601477094756.2第三年2783474101288475.2

注：数据来源于结合蛇屋山原始数据，运用上述模型模拟计算所得。

3.2 现有价格每年增长5元/g时的开采路径

当现有价格250元/g每年增长5元/g时，区块A、区块C及区块D达到最低工业品位，即需要在矿山净效益最大化目标下，在耗竭时间T内配置区块A、区块C及区块D各块段每年开采量。若价格以250元/g每年增长5元/g时，矿山可实现4年技术经济可采矿石量。价格变化时，最低工业品位随之发生变化，每年达到技术经济可采的区块及块段不同，详细情况参考如下最低工业品位及块段品位图(图3)。第一年，区块A技术经济可采矿石量完全开采，区块D技术经济可采矿石量部分开采；第二年，区块D技术经济可采矿石量部分开采；第三年，区块D剩余技术经济可采矿石量完全开采，区块C技术经济可采矿石量部分开采；第四年，区块C技术经济可采矿石量完全开采。具体产量和利润如表2所示。

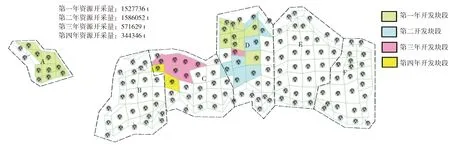
图3 金价年增5元/g下金矿开采量路径

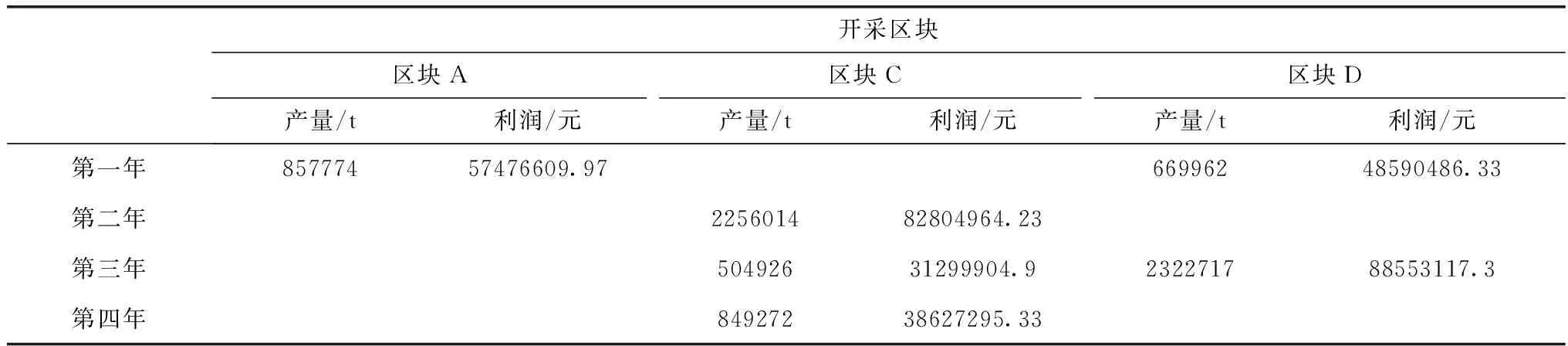
开采区块区块A区块C区块D产量/t利润/元产量/t利润/元产量/t利润/元第一年85777457476609.9766996248590486.33第二年225601482804964.23第三年50492631299904.9232271788553117.3第四年84927238627295.33

注：数据来源于结合蛇屋山原始数据，运用上述模型模拟计算所得。

3.3 现有价格每年增长15元/g时的开采路径

当现有价格250元/g每年增长15元/g时，区块A、区块C、区块D及区块E达到最低工业品位，即需要在矿山净效益最大化目标下，在耗竭时间T内配置区块A、区块C、区块D及区块E各块段每年开采量。若价格以250元/g每年增长15元/g时，矿山可实现5年技术经济可采矿石量(图4)。价格变化时，最低工业品位也变化，每年达到技术经济可采的区块及块段不同。第一年，区块A技术经济可采矿石量完全开采，区块D技术经济可采矿石量部分开采；第二年，区块D技术经济可采矿石量部分开采；第三年，区块D剩余技术经济可采矿石量完全开采，区块C技术经济可采矿石量部分开采；第四年，区块C技术经济可采矿石量完全开采，区块E技术经济可采矿石量部分开采；第五年，区块E剩余技术经济可采矿石量完全开采。具体产量和利润见表3。

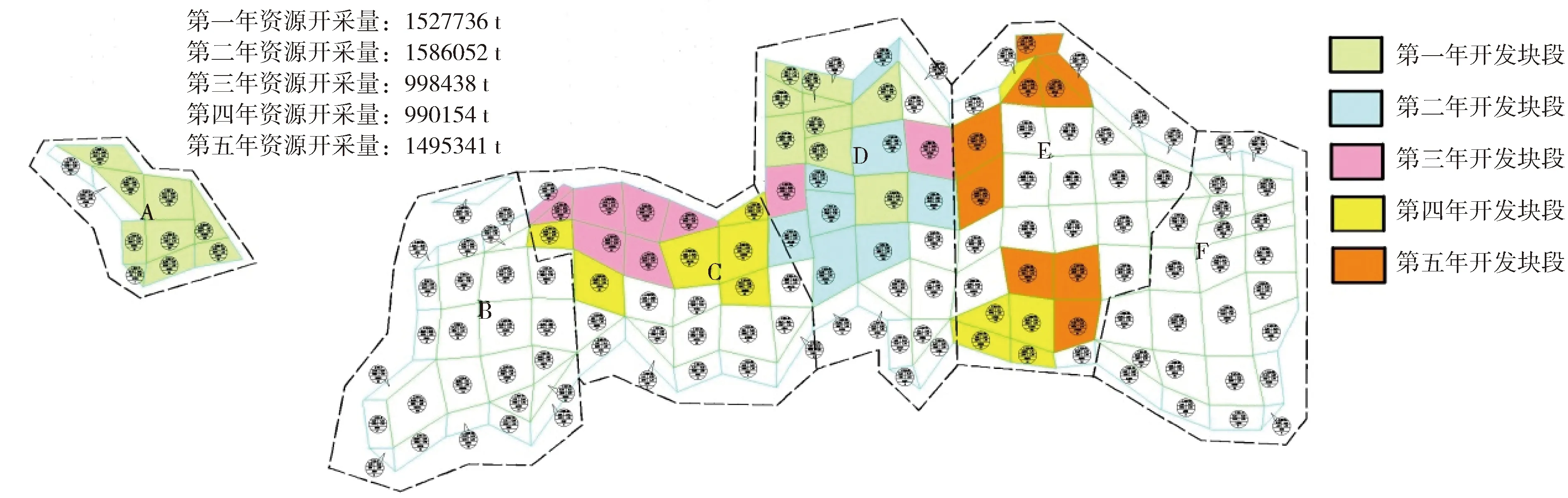
图4 金价年增15元/g下金矿开采量路径

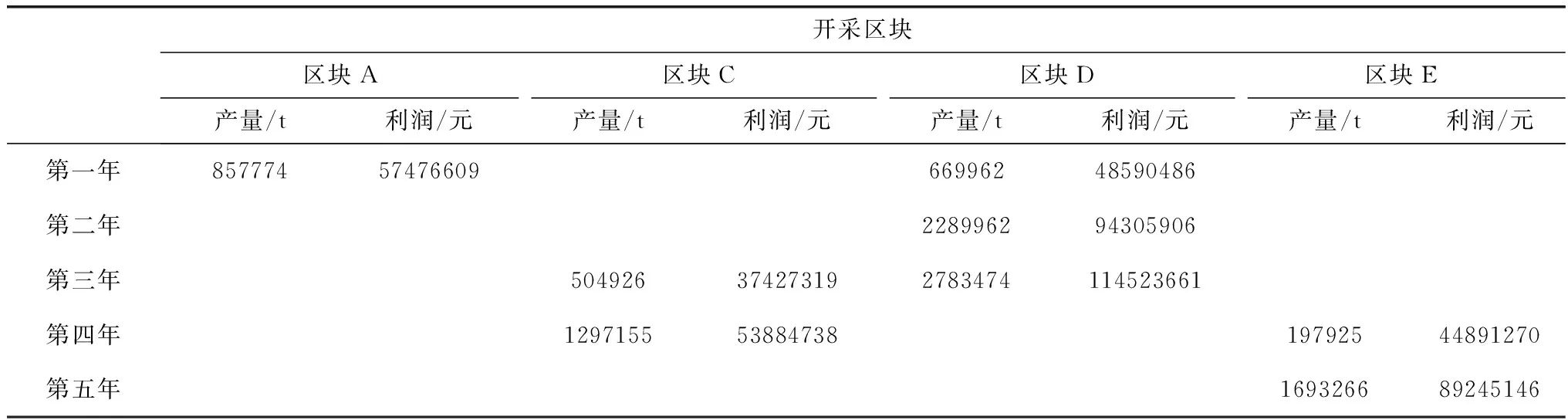
开采区块区块A区块C区块D区块E产量/t利润/元产量/t利润/元产量/t利润/元产量/t利润/元第一年8577745747660966996248590486第二年228996294305906第三年504926374273192783474114523661第四年12971555388473819792544891270第五年169326689245146

注：数据来源于结合蛇屋山原始数据，运用上述模型模拟计算所得。

4 结语

将矿山最优开采配置路径模型应用于蛇屋山金矿产资源的开采，结合最优控制理论，从时间和空间维度确定矿山不同区块的年开采资源3bgfvh配置路径，在保障矿山可持续发展的前提下，使得企业所得的利润最大化。研究结果给出了不同市场金价下矿山空白区资源最优开采路径区块的开发顺序，并通过比较分析得出若未来市场金价持续走高，会带动最低工业品味、开采技术水平等发生变化，去开采更加难以开采的金矿，从而实现更大的经济可采储量。因此，价格作为优化金矿开采路径的关键 因素之一，从全国角度来说，政府可通过调控金矿价格，实现矿区的可持续发展。

本文对矿山最优开采配置路径的实证研究，是建立在金矿山资源储量和资源耗竭时期假定的条件之上的，其中的参数设置也较理想化，未考虑实际应用中一些不确定因素的影响，将该模型应用于实际生产运营中还需要进行完善，这是今后研究努力的方向。

[1]Hotelling H.The Economics of Exhaustible Resources[J].Journal of Political Economy,1931,39(2):137-175.

[2]O.C.Herfindahl.Depletion and Economic Theory[M].edited by M.Gaffney: Extractive Resources and Taxation.University of Wisconsin Press,1967.

[3]Tietenberg T H,Lewis L.Environmental and natural resource economics[M].New York:Harper Collins,1992.

[4]魏晓平,王立杰.矿产资源价值与最佳耗竭速度研究[J].管理工程学报,1997，(6):122-126.

[5]杨海生,周永章,杨小强,等.不确定条件下矿产资源的最优开采[J].资源开发与市场.2005,21(5):398.

[6]葛世龙,周德群.储量不确定对可耗竭资源优化开采的影响研究[J].中国管理科学,2008,16(6):137-141.

[7]葛世龙,周德群.后备技术不确定下资源耗竭动态优化模型研究[J].管理科学学报,2010,13(4):23-28.

[8]胡静峰,张世全.矿产资源最优消耗效率模型及实证研究[J].求索,2011,(5): 17-19.

Research on Impacts of Golden Price on the Optimal Exploitation Path of Golden Mine in Shewu Mountain

WANGXin-qing1,XIONGYan2,ZHUBen-jie1

(1.The Fourth Geological Team of Hiubei Geologocial Bureau,Xianling 437100,China;2.College of Economic & Management,University of Geosciences,Wuhan 430074,China)

Gold mine of Shewu Mountain urgently need dynamic and sustainable development strategies to deal with the problems of mineral resource continuing consumption and the international gold price fluctuations.Basing on the theory of exhaustible resources,we aim to build a dynamic model of the Shewu Mountain to study the mining management,as well as maximize profits mine.Simulating of mining path with different ways,Shewu Mountain Gold resource allocation path can be determined from time dimension,and the configuration of a path can be determined from the spatial dimension blocks.As a result,the gold mining ore optimal can be decided from the amount of resource extraction different block segments.The results show the effectiveness of the model,and the model can draw the best path area development and exploitation of mining order blank area resources,and resources can be predicted with the changes in market prices,the mine’s economically recoverable reserves,in order to achieve exhaustible rational and efficient development and utilization of resources.

exhaustible resources;dynamic models;optimal extraction;mining path

10.3969/j.issn.1009-4210.2016.05.015

2016-04-29；改回日期：2016-06-16

中国地质调查局项目(12120114056501)

王庆新(1968-)，男，高级工程师，从事地质找矿与开发管理研究。E-mail:254106357@qq.com

F416

A

1009-4210-(2016)05-105-06