不同Halton抽样方法在混合Logit模型中的比较

史楠楠 诸立超

(同济大学交通运输工程学院道路与交通工程教育部重点实验室1) 上海 201804)(悉尼大学商学院交通运输与物流研究所2) 悉尼 2006)



不同Halton抽样方法在混合Logit模型中的比较

史楠楠1)诸立超1,2)

(同济大学交通运输工程学院道路与交通工程教育部重点实验室1)上海 201804)(悉尼大学商学院交通运输与物流研究所2)悉尼 2006)

以混合Logit模型参数估计中应用最广泛的四类Halton抽样方法为研究对象，包括Halton、变序Halton、乱序Halton和去随机化Halton，借助平均绝对百分误差箱型图比较不同维度、不同抽样方法得到的参数估计值，同时结合数百次模拟概率标准差判断不同抽样方法适用性.结果表明,在低维度情况下，各Halton抽样方法参数估计结果相差不大，且乱序Halton抽样性质与伪随机抽样无异；而随着维度的增加，几类Halton的抽样点均匀程度逐渐与伪随机抽样接近，且变序Halton抽样优于其他3类Halton抽样.

混合Logit模型；参数估计；伪随机抽样；Halton抽样

0 引 言

离散选择模型从随机效用最大化角度给定了个体选择衡量标准，从最简单的多项Logit模型(multinomial logit，MNL)一直到约束最少的混合Logit模型(mixed logit，ML)，参数估计方法也由极大似然估计(maximum likelihood estimation，MLE)拓展至极大模拟似然估计(maximum simulation likelihood estimation，MSLE).为能够利用ML模型研究面板数据和决策者异质性等问题，需使用蒙特卡罗方法(monte carlo method，MC)估计参数.MC的主要思想是对概率密度函数进行多次抽样，并以模拟概率均值作为积分近似解.自Train将Halton抽样引入ML模型参数估计后，又有许多学者将Halton抽样及其变形(变序Halton序列等)及其他低差异序列(Faure序列等)引入进来，极大丰富了ML模型参数估计中所使用的抽样方法.

Train[1]通过比较ML模型概率的模拟方差(simulation variance)，得出Halton抽样远优于伪随机抽样(pseudo-random sampling)的结论.Bhat[2]从参数估计角度也得到了类似结论，其评价指标包括均方根误差(root mean square error，RMSE)、平均绝对百分误差(mean absolute percentage error，MAPE)和收敛时间(time to convergence，TTC)指标.此后，Bhat[3]进一步引入变序Halton(Scrambled Halton)抽样，在多项Probit模型应用中比较3种方法，最后认为变序Halton抽样最优，Halton抽样次之.Hess等[4]则比较了包括Halton抽样、变序Halton抽样和乱序Halton(Shuffled Halton)抽样等在内的3类抽样方法，虽然后两者均存在解决Halton相关性的潜力，但作者认为变序Halton抽样在一定程度上并不稳定，并且维度局限于16维以下.Hess等[5]在3类Halton抽样基础上增加修正拉丁超立方体抽样(modified latin supercube sampling，MLHS)估计16维参数，得到MLHS最优的结论.有趣的是，这4类方法与伪随机抽样的均方根误差相差不大，Hess等认为，一维数列未结构化组合得到的多维序列性质会随维度的增加而逐渐趋近于伪随机抽样.Status[6]对伪随机抽样、Halton抽样和乱序Halton抽样的研究结论与以往不同，认为虽然乱序Halton抽样减小了Halton抽样高维度的相关性、提高了抽样分布均匀度，但从参数估计结果和极大似然值来看，利用乱序Halton抽样得到的结果反而比Halton抽样差，仅在少数情况下优于Halton抽样.

鉴于目前尚无证据表明某一种低差异序列明显优于另一种序列，并且学者们也未对几种Halton抽样的优劣形成统一意见，因此文中仍对Halton序列进行研究.文中的主要贡献在于：(1)既有研究并未结合参数估计和概率计算两方面结论比较抽样方法优劣，文中借助箱型图和平均绝对百分误差指标比较分析各Halton抽样方法优劣；(2)现有文献对乱序Halton抽样是否优于Halton抽样和变序Halton抽样持有两种截然不同的观点，文中针对这一问题研究得到相应结论.

1 伪随机抽样

所谓随机序列，就是后一个数与前一个数无关的序列，真正的随机数使用,例如,掷钱币等物理现象产生，缺点在于技术要求较高，而在实际应用中往往使用伪随机数便能满足大部分要求.伪随机数看似随机，实际由固定、可重复的算法生成，并非真正随机.伪随机数的生成主要根据如下3种方法：(1)直接法(direct method)；(2)逆转法(inversion method)；(3)接受拒绝法(acceptance-rejection method)[7].文中采用逆转法生成伪随机数，首先生成[0,1]之间服从均匀分布的随机数U，假设U服从的累积分布函数为F，根据X=F-1(U)求得最终随机数.

2 Halton抽样及其变形

2.1 标准Halton抽样

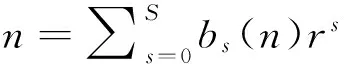
相比于伪随机抽样，Halton抽样存在如下优点：(1)在绝大部分积分区域内，抽样点分布十分均匀；(2)下一次抽样点与上一次抽样点存在负相关性，即下一次抽样点可填补上一次抽样点未包含的区域，提高了抽样点覆盖率.

2.2 变序Halton抽样

Halton序列的主要问题在于高维度序列的相关性，导致积分区域抽样不均并引起积分误差.此问题并不仅仅针对高维度质数，主要由两个质数之比过分接近于1所引起.变序Halton抽样的想法最初由Braaten等[8]提出，旨在改善高维度Halton序列的均匀度.基本思想是打乱以r为数基、循环长度为r的Halton序列，从而降低不同维度间的相关性.通过变换b1(n)…bS(n)顺序(见表1)得到变序Halton序列，并且变换后的序列仍保持Halton序列N-1(N为抽样数)的积分误差.

表1 变序Halton序列变换

2.3 乱序Halton抽样

乱序Halton抽样最初由Morokoff等[9]于1994年提出，为一种采用独立随机向量变换Halton序列的方法，随后被Hess等[10]命名为乱序Halton序列.由前文可知，所生成的Halton序列和变序Halton序列固定，即每次生成序列不发生变化，而生成乱序Halton序列需融合Halton序列和伪随机数，生成序列与随机种子的设置相关.产生机理如下：(1)首先产生以r为数基、长度为N的Halton序列；(2)然后生成同样长度的伪随机序列，Halton序列与伪随机序列一一匹配；(3)伪随机序列从小到大(或从大到小)排列，相应地，变换Halton序列顺序得到一维乱序Halton序列.若需生成d维乱序Halton序列，则应生成d维伪随机序列(不同随机种子)，然后根据步骤(3)便可生成d维乱序Halton序列.Hess等已证明乱序Halton序列比变序Halton序列更有潜力提供更佳的多维积分区域抽样覆盖率，但Schlier[11]认为乱序Halton抽样并非低差异序列，其表现与伪随机抽样相近，下文也将探讨这一问题.

2.4 去随机化Halton序列

线性加扰是消除Halton序列相关性的简单有效的方法，文中借鉴去随机化Halton序列，基于数字置换变换Halton序列：

式中：φπri(n)为集合{0,1,2,…,ri-1}的置换.采用线性函数f(x)=wx进行加扰：

(2)

前12维去随机化Halton序列的wi最优值见表2.

表2 去随机化Halton序列的wi最优值

3 抽样方法比较

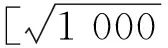
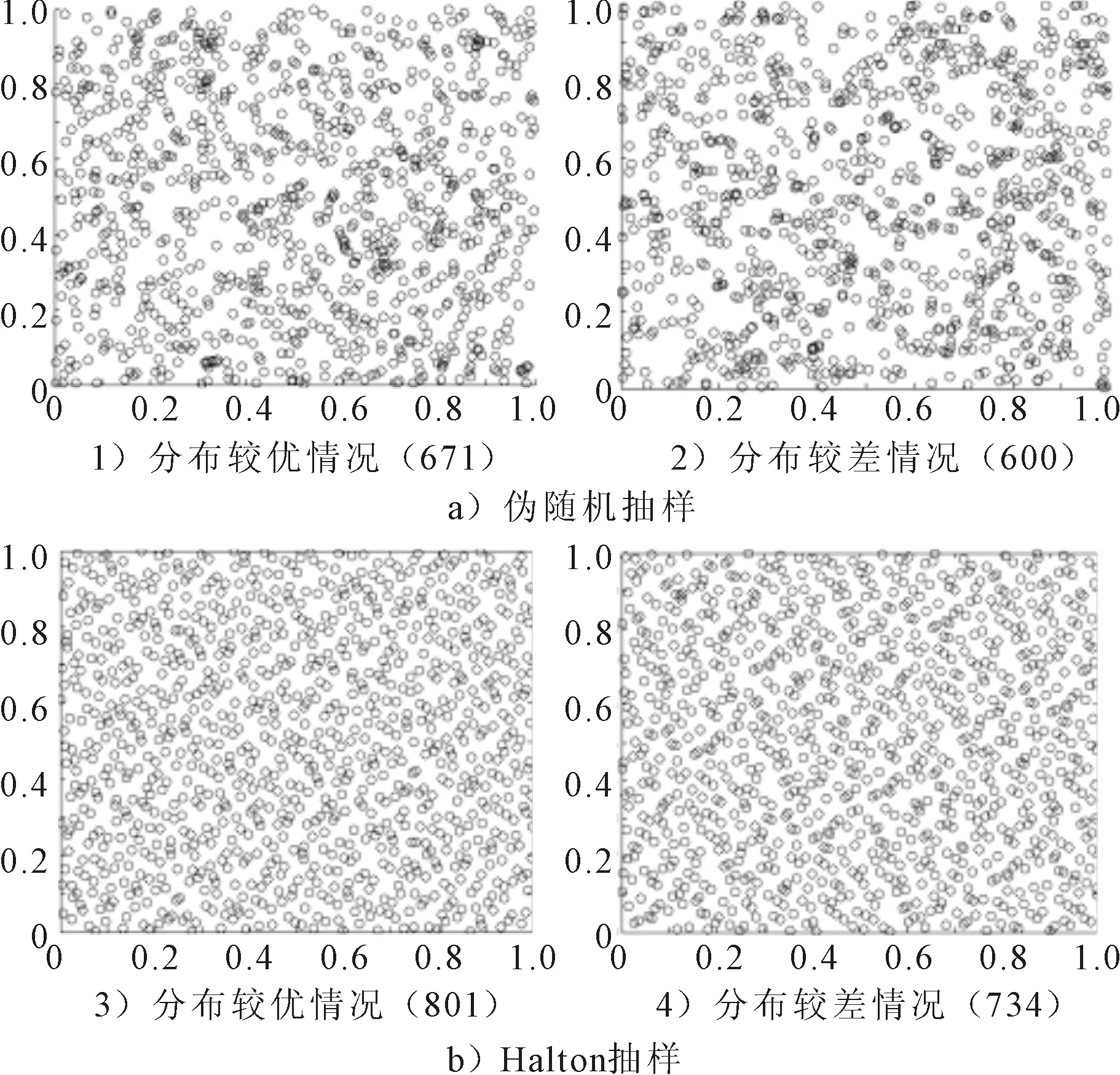
图1 二维抽样点分布图

下面以二维序列为例，进一步比较不同Halton抽样所得抽样点分布情况，选取低维质数2、3及高维质数59，61绘制100个抽样点的分布图，见图2、图3.

图2 以2,3为数基的Halton序列二维点分布图

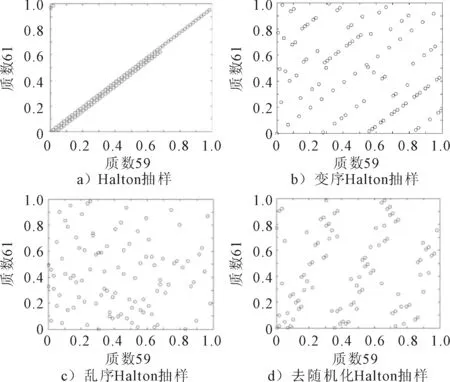
图3 以59,61为数基的Halton序列二维点分布图

由图2、图3可见，当使用低维度质数时，直观感觉乱序Halton抽样点分布不如其他3类Halton抽样均匀，其余3类Halton抽样点均匀度并无显著差异；但随着使用质数维度的增加，如使用第17和18维质数时，由于高维度质数序列相关性导致Halton抽样表现越来越差，见图3a)；而乱序Halton抽样表现基本不变，变序Halton抽样和去随机化Halton抽样也可在一定程度上减轻Halton抽样相关性问题.

4 混合Logit模型参数估计结果比较

4.1 混合Logit模型

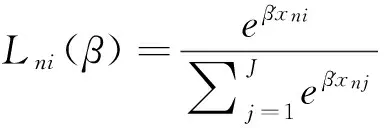
(3)

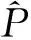
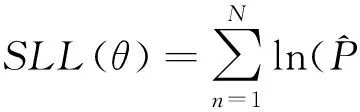
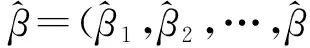
(4)

这一指标越小说明得到的参数估计值与参数真值越接近，表明抽样方法越好.

4.2 参数估计结果

伪随机抽样和乱序Halton抽样会因每一次随机种子选取的不同而产生不同序列，Halton抽样、变序Halton抽样和去随机化Halton抽样则保持不变.考虑到Halton抽样前几次抽样点相关性较高，因此在第i次抽样时，舍去前10×i个数，也可参考Tuffin对Halton序列作随机化处理.文中所采用的数据为决策者对三种动力汽车(电力、天然气和混合动力)的选择数据，主要变量有价格、高性能、中高性能、运行费用、行驶距离范围和哑元(电力和混合动力)等，文中不再赘述具体数据，详见文献[12].下文针对1至3个随机参数的情况采用不同抽样方法估计参数.

首先比较一维情况下的4类Halton抽样，见图4.由图4可知，(1)Halton抽样与变序Halton抽样相同，并且均优于去随机化Halton，紧接着是抽样次数较多(250次)的随机抽样，乱序Halton表现最差；(2)随着抽样次数的增加，除去随机化Halton略优于Halton和变序Halton外，其余Halton抽样优劣保持不变，100(150)次Halton抽样和变序Halton抽样基本相同，略优于500(1000)次伪随机抽样.

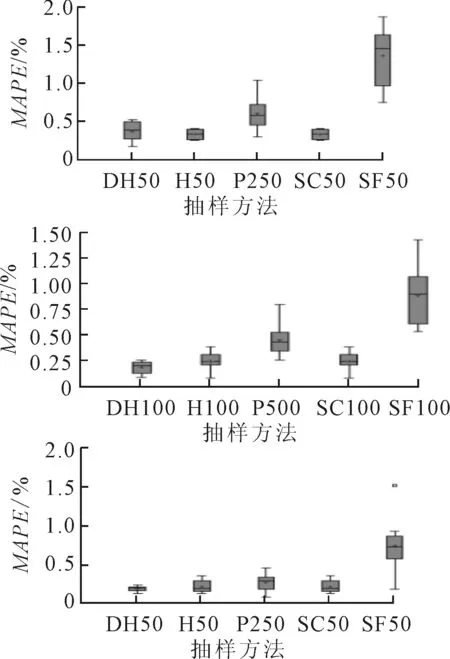
图4 一维参数估计结果比较(质数：2)

在二维情况下：(1)去随机化Halton抽样最优，乱序Halton抽样的表现始终最差；(2)伪随机抽样与4类Halton抽样的差异要比在一维情况下有所减小，甚至因抽样次数较多而优于4类Halton抽样，这在一定程度上证实随着维度的增加，Halton抽样会逐渐向伪随机抽样靠拢的结论.

在选用质数2,3和5作为数基的三维情况下，4类Halton抽样除乱序Halton抽样外，不同抽样次数下的抽样方法各有优劣，不能得到明确结论；而选用较大质数43、47和53作为数基时，结果发生明显转变，变序Halton和乱序Halton抽样要优于其他2种抽样，而变序Halton抽样最佳，表明在高维情况下使用较大质数生成的变序Halton抽样和乱序Halton抽样更优.

通过比较不同维度、不同质数的Halton抽样，可知乱序Halton抽样的表现与伪随机抽样类似，在低维情况下始终是4类Halton抽样中最差的，造成这一结果的原因是低维Halton序列不存在严重相关性，对其进行随机化并不能起到改善作用，反而会使均匀度下降，但随着维度的增加，其他Halton抽样表现的恶化反而凸显出乱序Halton抽样的优势.

DH50为50次去随机化Halton抽样)；H50为50次Halton抽样；P250为250次伪随机抽样；SC50为50次变序Halton抽样；SF50为50次乱序Halton抽样.图5～图8中的横坐标代表的参数依此类推.

图5 二维参数估计结果比较(质数：2和3)

图6 三维参数估计结果比较(质数：2,3和5)

图7 三维参数估计结果比较(质数：43,47和53)

图8 三维参数估计结果比较(质数：83,89和97)

4.3 概率计算结果

进一步根据如下方法研究模拟概率性质：选取某一样本，结合上文所得3个随机参数的估计结果，利用不同抽样方法模拟该样本概率1000次，假设每次模拟抽样数为R，则序列长度为1 000×R+10(删去前10个Halton抽样点).表3给出了使用不同数量、不同抽样方法的模拟概率统计量.标准差越小表明模拟概率越稳定、抽样点分布越均匀，根据不同抽样方法的1 000次模拟概率标准差可知：(1)当抽样使用低维质数时，Halton抽样以极小优势优于变序Halton抽样，紧接着是去随机化Halton抽样，乱序Halton抽样表现最差；(2)当抽样使用高维质数时，伪随机抽样和乱序Halton抽样表现与使用低维质数时几乎不变，乱序Halton抽样表现略有下滑，而去随机化Halton抽样表现下滑幅度最明显.

表3 不同抽样方法及抽样次数下的模拟概率统计量

5 结 束 语

文中从ML模型参数估计和模拟概率计算两方面比较不同Halton抽样优劣.在低维度情况下，除乱序Halton抽样以外的其余3类Halton抽样相对表现会随抽样次数的变化而波动，各有优劣，乱序Halton抽样表现始终最差，其性质并未优于伪随机抽样；而随着维度的增加，这一结论逐渐发生反转，由于高维度Halton抽样序列存在相关性，使原本表现不佳的乱序Halton抽样逐渐好转，并与变序Halton抽样相差无几；此外，结合模拟概率统计量，证实了变序Halton抽样会随维度的增加，逐渐成为几种Halton抽样中最佳的结论.不难推论，当随机参数数量较少时，使用变序Halton抽样所得参数估计值更加精确；而当随机参数数量较多时，可能使用伪随机抽样所得参数估计值更为精确.但由于数据受限，文中未对高维度下的各种抽样方法进行全面比较，所得结论仍需进一步论证，同时变序Halton抽样与伪随机抽样在多少维度时表现相同也值得深入研究.

[1]TRAIN K. Halton sequences for mixed logit[EB/OL].(1999-08-02)[2016-03-22]. http://elsa.berkeley.edu/wp/train0899.pdf.

[2]BHAT R C. Quasi-random maximum simulated likelihood estimation of the mixed multinomial logit model[J]. Transportation Research Part B: Methodological,2001,35(7):677-693.

[3]BHAT R C. Simulation estimation of mixed discrete choice models using randomized and scrambled Halton sequences[J]. Transportation Research Part B: Methodological,2003,37(9):837-855.

[4]HESS S, POLAK J W. On the performance of shuffled Halton sequences in the estimation of discrete choice models[EB/OL].(2003-06-08)[2016-03-22].http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.110.3610&rep=rep1&type=pdf.

[5]HESS S, TRAIN K, POLAK J W. On the use of a modified latin hypercube sampling (MLHS) method in the estimation of a mixed logit model for vehicle choice[J]. Transportation Research Part B: Methodological,2006,40(2):147-163.

[6]STAUS A. Standard and shuffled Halton sequences in a mixed logit model[EB/OL].(2008-09-07)[2016-03-22].https://marktlehre.uni-hohenheim.de/fileadmin/einrichtungen/marktlehre/Arbeitsberichte/haa_nr17.pdf.

[7]DíAZ C N, GIL A V, VARGAS M J. Assessment of the suitability of different random number generators for monte carlo simulations in gamma-ray spectrometry[J]. Applied Radiation and Isotopes,2010,68(3):469-473.

[8]BRAATEN E, WELLAR G. An improved low-discrepancy sequence for multidimensional quasi monte carlo integration[J]. Journal of Computational Physics,1979,33(2):249-258.

[9]MOROKOFF W J, CAFLISCH R E. Quasi-random sequences and their discrepancies[J]. Society for Industrial and Applied Mathematics,1994,15(6):1251-1279.

[10]HESS S, POLAK J W. The shuffled Halton sequence[R]. Centre for Transport Studies (CTS) Working paper,2003.

[11]SCHLIER C. On scrambled Halton sequences[J]. Applied Numerical Mathematics,2008,58(10):1467-1478.

[12]TUFFIN B. On the use of low discrepancy sequences in monte carlo methods[J]. Monte Carlo Methods and Applications,1996,2(4):295-320.

Comparison of Different Halton Sampling Methods in Mixed Logit Model

SHI Nannan1)ZHU Lichao1,2)

(CollegeofTransportationEngineering,KeyLaboratoryofRoadandTrafficEngineeringoftheMinistryofEducation,TongjiUniversityShanghai201804,China)1)(InstituteofTransportandLogisticsStudies,TheBusinessSchool,TheUniversityofSydney,NSW2006,Australia)2)

Several Halton sampling methods which are widely used in mixed logit model parameter estimation are taken as the research objects, including Halton, scrambled Halton, shuffled Halton and derandomized Halton sampling. Based on box plot of mean absolute percentage error, parameter estimators of different Halton samplings are compared under different dimensions. Meanwhile, standard error of hundreds of probability simulation is analyzed to judge the applicability of different methods. The result shows that: under low-dimension, all Halton sampling methods have almost no difference in parameter estimation results, and shuffled Halton sampling is the same as pseudo random sampling; with the increase of dimension, distribution uniformity of sampling points from Halton sampling methods is gradually approaching to pseudo-random sampling, while the scrambled Halton sampling is better than the other three Halton sampling methods.

mixed logit model; parameter estimation; pseudo sampling; Halton sampling

2016-08-20

U491 doi:10.3963/j.issn.2095-3844.2016.05.030

史楠楠(1992- )：女，硕士生，主要研究领域为交通运输规划与管理、离散选择建模