多模态双层隔振系统多输入输出耦合反馈振动控制研究*
刘树勇 方 远 位秀雷
(海军工程大学动力工程学院 武汉 430033)
多模态双层隔振系统多输入输出耦合反馈振动控制研究*
刘树勇 方 远 位秀雷
(海军工程大学动力工程学院 武汉 430033)
建立了双层隔振系统多输入输出反馈振动控制模型,研究了在双反馈控制作用下,隔振系统的力传递率特征.分析了反馈环节中控制力、耦合系数,以及作动器位置振动速度之间的关系,并研究了作动器之间的互相耦合对系统稳定性和力传递效果的影响.通过Nyquist稳定性分析,得到了系统在不同参数条件下的稳定性及随参数变化的规律.仿真结果表明,多反馈控制过程中系统具有鲁棒性,耦合系数的增加使振动隔离能力更好.
多模态;双层隔振系统;稳定性分析;多反馈控制
0 引 言
由于被动隔振系统的局限性,对振动系统进行主动控制成为了振动控制的重要手段之一.国内外学者对该问题进行了广泛深入的研究,主要包括主动控制算法、作动器和隔振系统的设计等[1].Mou等[2]应用PID控制器对悬架系统的振动进行了控制,将输出降低到激励的1%左右.Ahn等[3]应用神经网络反馈控制器对主被动混合隔振系统进行了控制,其中空气弹簧作为被动隔振元件,电磁作动器作为主动元件.Serrand等[4]对基础激励条件下的多通道反馈控制算法进行了研究,通过速度反馈控制,使被保护精密仪器的振动隔离效果明显增加,并通过实验研究了控制系统的鲁棒性.Schubert等[5]对六通道悬挂式主动阻尼器进行了研究,显著地减少悬挂质量的振动.由于非线性的影响,使得控制问题更加复杂,为此Mori等[6]研究了MR阻尼器非线性迟滞动力学特性的补偿方法;Adam等[7]则研究了悬架系统半主动振动控制的非线性动力学特性;Liang等[8]研究了悬架混沌振动控制模型.在智能控制方面, Youn等[9]研究了复合梁结构的神经自适应控制算法;Kumar等[10]研究了变参数智能结构的MIMO自适应的振动控制算法.Kerber等[11]提出了六自由度主动振动控制的模型,并设计了作动器,将系统由SISO改进为MIMO.Kimihiko等[12]提出应用自振产生的能量进行主动控制的思路,即自功率主动振动控制系统.然而多通道耦合反馈主动隔振的研究还缺乏深入研究,从而使得多作动器的优化设计和控制缺乏有效参考.文中建立多通道多自由度隔振系统的耦合反馈隔振模型,推导控制力、反馈矩阵和振动之间的关系,并分析系统的稳定性,为振动控制系统设计提供理论参考.
1 多输入输出反馈的耦合
两自由度双输入输出反馈控制隔振系统的简化模型见图1.包括上下层质量块M1,M2;振动传感器,上层弹簧元件,其刚度为K1,下层弹簧元件,其刚度为K2;上下层质量块质心的振动位移分别为X1,X2;激励力的幅值为F,激励频率为Ω;力反馈作动器P1和P2并联安装在上下层质量之间,其反馈为上层不同测点的振动位移响应.
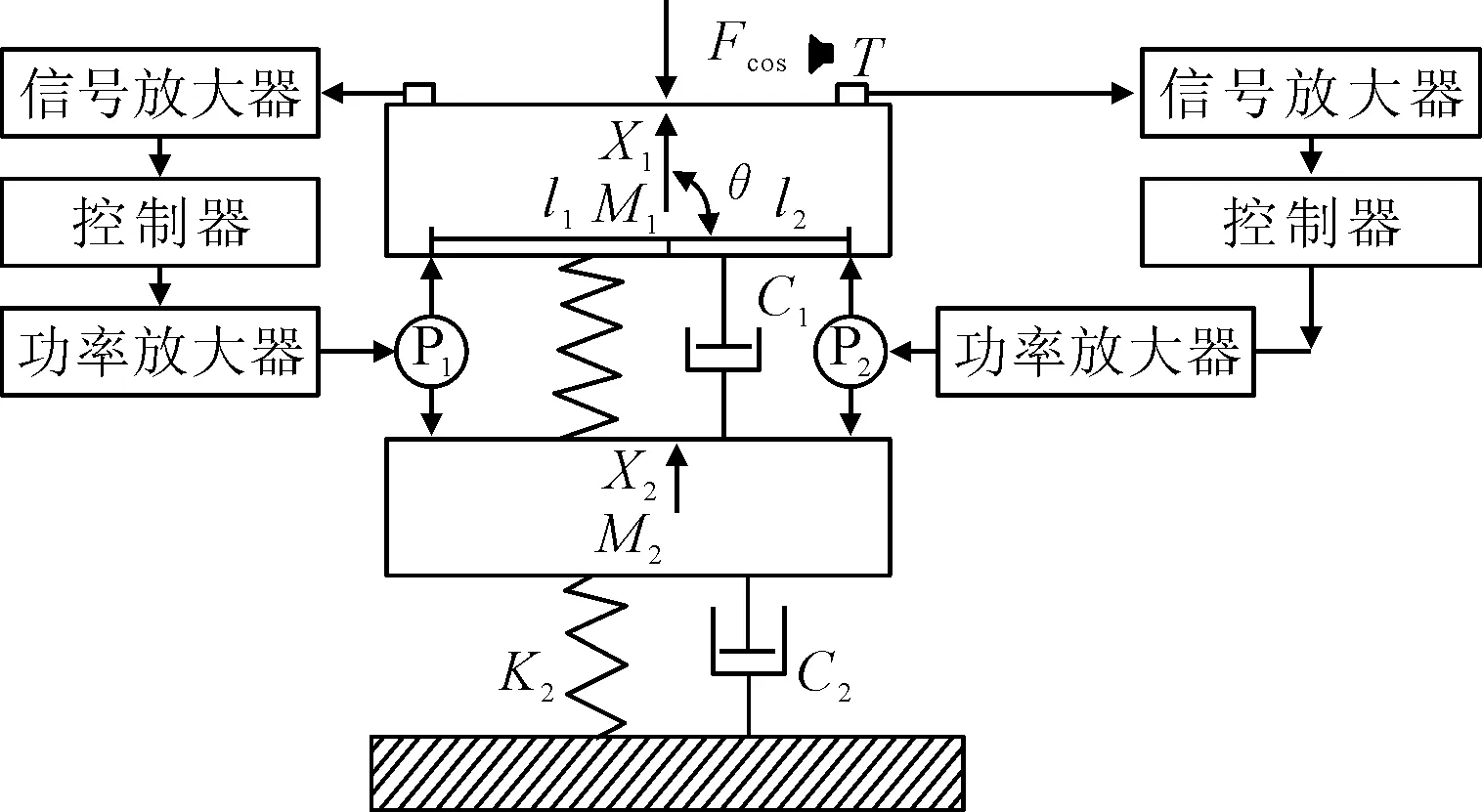
图1 双层隔振系统多输入反馈控制图
在工程实际中,由于隔振器之间的差异或者环境因素,考虑上层质量块存在垂向运动模态和绕质心的旋转的多模态运动时,2个测点的位置的位移响应信号也将存在一定的差异,表示为Xu=(Xu1,Xu2)T.耦合作用的存在,因此控制信号u=(u1,u2)T和振动速度响应之间的关系为
(1)
而2个作动器产生的力fs为
(2)

进一步分析作动器之间的在耦合作用.考虑到作动器作用位置的振动速度的变化,v=(vu1,vu2)T,它是由系统激励力和作动器控制力耦合作用下产生的,为v=ve+va,其分量形式为
式中:vei(i=1,2)为激励力作用产生的速度变化分量;vai(i=1,2)为控制力作用产生的速度变化分量;
(3)
它们综合反映了控制力、耦合系数、作动器位置振动速度之间的相互关系.
2 多输入耦合反馈的传递函数分析
隔振系统带反馈控制时的传递函数框图见图2,其中实线表示力信号流向,虚线表示位移信号流向.多输入输出反馈通道由Φ(s)和T(s)组成,它们由式(1)、式(2)确定.要使得向基础传递的力小,作动器下端的力必须与质量块M2上的原受力方向相反.
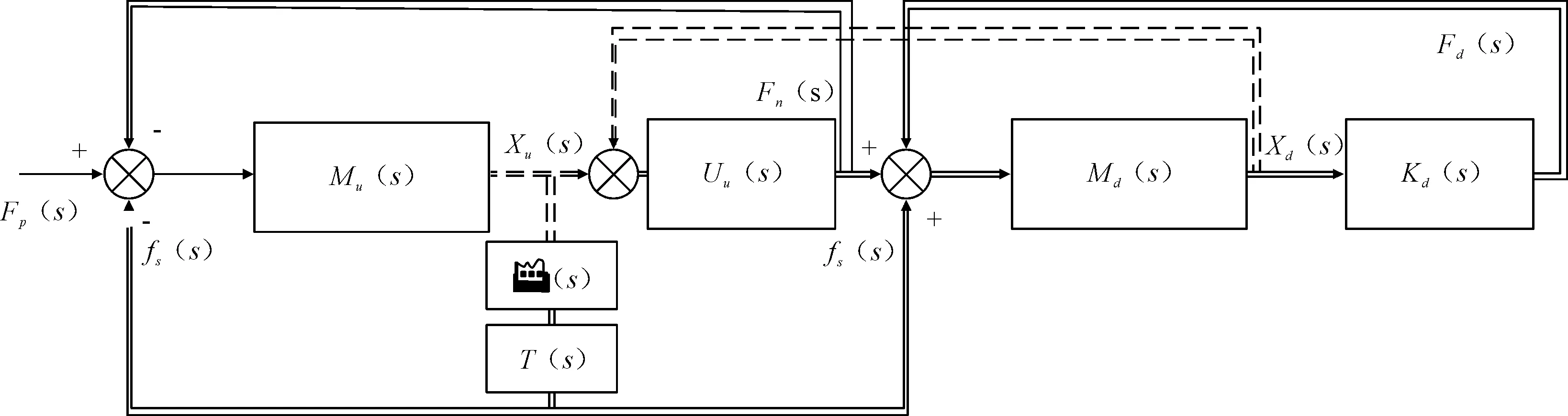
图2 振动系统整体控制框图
Ku(s)=C1s+K1,Kd(s)=C2s+K2假设传感器位置的位移和质心之间的位移满足如下关系
(4)式中:l1,l2为作动器到中心的距离;θ为上层量块转动的较小的角度.因此,可以得到
(5)
(6)
(7)
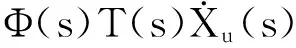
(9) 记:G(s)=Φ(s)T(s),G=gij(i,j=1,2).因此
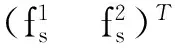
(11) 由于式(11)中{ψ1(-g11l1+g12l2)+ψ2(-g21l1+g22l2)}θ项比较小,简化为
(12) 因此,由式(8)和式(12)得到X1(s)和X2(s)之间满足如下关系
(13) 作用在弹性基础上的力为
(14) 力传递率可以表示为
(15)
综合式(10)和(15)分析,得到带双输入反馈隔振控制系统中激励力和基础上作用力之间的传递函数H(s)的表达式为
(16)
利用式(13)中X2(s)/X1(s)的关系得到
(17)
其中:Z1=Mu(s)-1+(C1s+K1)+ψ1(g11+g12)s+ψ2(g21+g22)s,Z2=Md(s)-1+Kd(s)+(C1s+K1),Z3=ψ1(g11+g12)s+ψ2(g21+g22)s+(C1s+K1).
3 四仿真研究
3.1 稳定性分析与阶跃响应
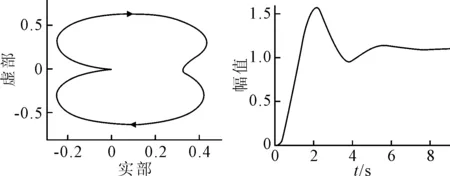
图3 Nyquist稳定判定和阶跃响应
由图3中可知,根据Nyquist稳定性标准可以知道系统右平面内没有极点,因此处于稳定工作状态.为了研究不同参数的影响,改变参数值观察其稳定性和系统响应的变化情况.当C的值减小时, C1=C2=0.5时,系统的稳定性图和响应图见图4.根据Nyquist稳定判定,在图4a)中,系统不包含(-1,0)的点,表明系统在右复平面内不包含不稳定的极点,因而系统稳定.根据阶跃响应上分析,虽然系统最后趋于特定位置,但其响应超调100%以上,稳定时间成倍增加,这种控制系统的效果也是非常不理想的.

图4 阻尼参数减小时的Nyquist稳定判定和阶跃响应
改变作动器之间的耦合系数,观察其对稳定性和系统响应的影响.当作动器耦合系数增加时,分别由10%g11增加为20%g11和40%g11时,结果见图5.由图5a)可知,增加20%时,系统处于稳定状态.由图5c)可知,增加到40%g11时系统稳定性也不发生变化,因而这种系统具有很强的鲁棒性.
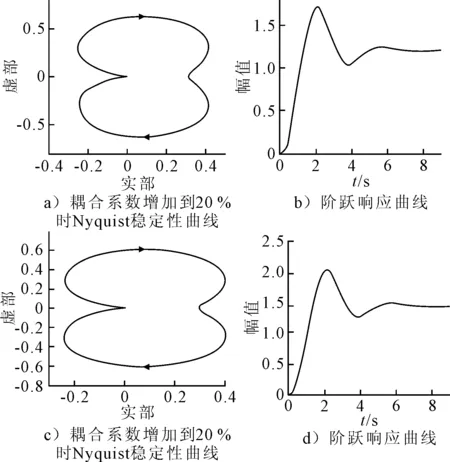
图5 耦合系数增加时的Nyquist稳定判定和阶跃响应
3.2 传递率曲线
根据稳定性分析,取反馈增益为15,耦合系数为2.5,约为16.7%,计算该系统的力传递率曲线.
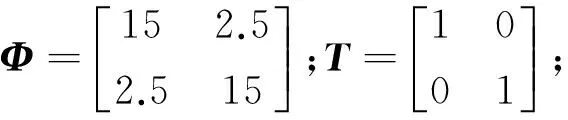
M1=20;M2=300;K1=20;
K2=300;C1=C2=25
仿真结果见图6.由图6a)可知,根据Nyquist稳定性准则,系统是稳定的.力传递率曲线见图6b),当没有反馈控制时,低频位置具有较大的峰值.当采用反馈增益为15,耦合系数为2.5时,峰值明显下降约8 dB,具有较好的低频振动隔离效果.其次,当作动器耦合系数从2.5增大为10时,得到的结果见图6d),此时系统仍然稳定.对两种情况下的力传递率曲线进行了比较,发现耦合系数增大时,在低频段的力传递率有进一步降低.总的趋势是有反馈控制时,有效工作频段在低频段.
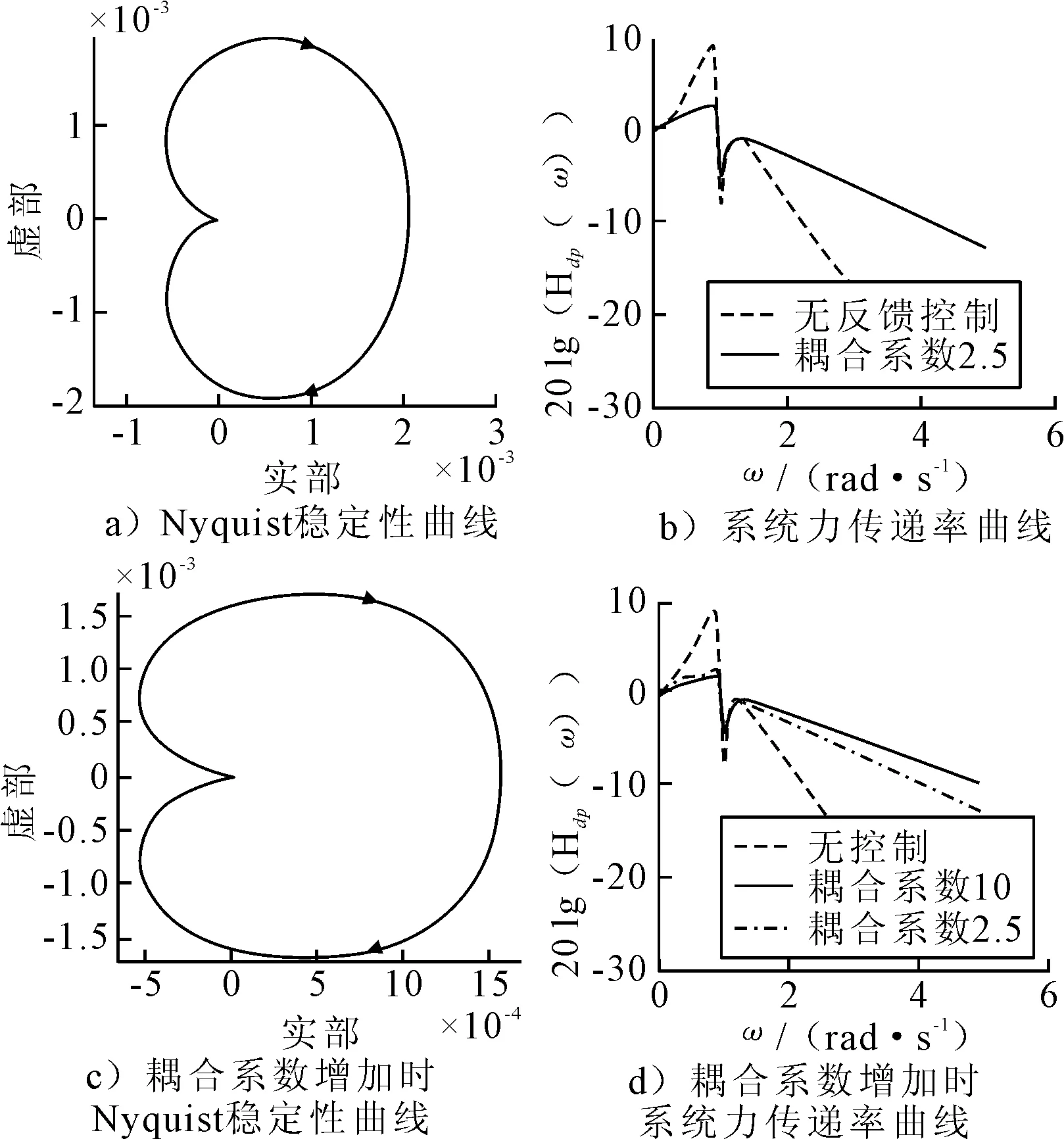
图6 耦合系数变化时稳定性曲线和力传递率曲线
4 结 束 语
建立多输入多输出耦合反馈控制模型,刻画了主动振动隔离系统中控制力、耦合系数、作动器位置振动速度之间的关系.研究表明,速度反馈耦合矩阵在运动方程中的本质作用调整了系统的阻尼参数,耦合系数大小反映了作动器之间的相互影响.应用Nyquist稳定性理论对系统的稳定进行了分析,既保证了控制系统处于稳定工作状态,又使系统有良好的振动隔离效果.得到了系统的传递率曲线以及耦合系数对传递率曲线的影响规律.增大耦合系数,可以使低频振动隔离效果更优.由于实际控制系统中,采用数字控制技术进行数据处理和控制,因此还需要深入研究延迟时间、采样速率以及系统的非线性等对系统的影响.
[1]BEARD A M, SCHUBERT D W, BRIGHTON N. A practical product implementation of an active/passive vibration isolation system[J]. Vibration Monitoring and Control,1994(2264):38-49.
[2]MOU R Q, LI H. Study of automobile suspension system vibration characteristics based on the adaptive control method[J]. International Journal of Acoustics and Vibration,2015,20(2):101-106.
[3]AHN K G, PAHK H J, JUNG M Y.A hybrid-type active vibration isolation system using neural networks[J]. Journal of Sound and Vibration,1996,192(4):793-805.
[4]SERRAND M, ELLIOTT S J. Multichannel feedback control for the isolation of base-excited vibration[J]. Journal of Sound and Vibration,2000,234(4):681-704.
[5]SCHUBERT D W. Characteristics of an active vibration isolation system using absolute velocity feedback and force actuation[C]. Proceedings of the Conference on Recent Advances in Active Control of Sound and Vibration, Blacksburg, Virginia,1991:448-463.
[6]MRORI T, NILKHAMHANG I, SANO A. Adaptive semi-active suspension system by linearly parameterized controller[C]. Pro. SICE Annual Conference,2007:1275-1280.
[7]ADAM A A, GULEZ K, ALISKAN I.Steering DTC algorithm for IPMSM used in electrical automobile(EV) with fast response and minimum torque ripple[C]. Proc. 11th IEEE International Workshop on Advanced Motion Control, Nagaoka, Japan,2001:279-283.
[8]LIANG S, ZHENG J, ZHU Q, et al. Numerical and experimental investigations on chaotic vibration of a nonlinear vehicle model over road excitation[J]. Journal of Mechanical Strength,2011,34(1):7-11.
[9]YOUN S H, HAN J H, LEE I. Neuro-adaptive vibration control of composite beams subject to sudden delamination[J]. Journal of Sound and Vibration,2000,238(2):215-231.
[10]KUMAR R, SINGH S P, CHANDRAWAT H N. MIMO adaptive vibration control of smart structures with quickly varying parameters: neural networks vs classical control approach[J]. Journal of Sound and Vibration,2007,307(3):639-661.
[11]KERBER F, HURLEBAUS S, BEADLE B M. Control concepts for an active vibration isolation system[J]. Mechanical Systems and Signal Processing,2007(21):3042-3059.
[12]KIMIHIKO N, YOSHIHIRO S, SHIGEYUKI N. Self-powered active vibration control using a single electric actuator[J]. Journal of Sound and Vibration,2003,260(2):213-235.
Study on the MIMO Coupling Feedback Vibration Control of the Multiple Modes Double Stage VIS
LIU Shuyong FANG Yuan WEI Xiulei
(CollegeofPowerEngineering,NavalUniversityofEngineering,Wuhan430033,China)
The multiple input multiple output (MIMO) coupling feedback of two stage vibration isolation system (VIS) is presented. The force transmissibility characteristic of the system is analyzed by double feedback control strategy and the relationship among the secondary force, coupling coefficient, and vibration velocity is disclosed. Then, the effects of the coupling coefficient on the stability and transmissibility are researched. The stability and the corresponding variation law under different parameters are discussed. Results show that the coupling system is robust and increasing the coupling coefficients improves the vibration isolation performance.
multi-mode; double stage vibration isolation system; stability analysis; multi-feedback control
2016-08-29
*国家自然科学基金项目(51179197, 51579242)、国家自然科学基金青年基金项目(51509253)资助
TN911 doi:10.3963/j.issn.2095-3844.2016.05.004
刘树勇(1975- ):男, 博士,副教授,主要研究领域为轮机工程

