射弹动力学方程的修正与超空泡形态
何生生侯坤元刘诗琪吴明和滕保华
(1电子科技大学微电子与固体电子学院,四川成都 610054;2电子科技大学通信与信息工程学院,四川成都 610054;3电子科技大学物理电子学院,四川成都 610054)
射弹动力学方程的修正与超空泡形态
何生生1侯坤元2刘诗琪2吴明和3滕保华3
(1电子科技大学微电子与固体电子学院,四川成都 610054;2电子科技大学通信与信息工程学院,四川成都 610054;3电子科技大学物理电子学院,四川成都 610054)
超空泡的形成对水下高速射弹运动有着非常重要的影响,为了更加全面地反映超空泡对水下射弹运动的作用以及超空泡的形态变化规律,通过对通常的射弹动力学方程进行修正,并结合Logvinovich原理,得到了在超空泡的影响下水下射弹的速度和位移的解析表达式,同时结合数值仿真研究了水下射弹运动过程中产生的超空泡形态的变化规律.解析分析和数值仿真结果表明,如果修正项系数越大,将导致射弹速度衰减得越快,完整空泡扩展时间越短,空泡长度越小,以及最大空泡截面半径越小,从而越不利于超空泡的形成.
射弹动力学方程;超空泡;Logvinovich方程
通常水下射弹在高速运动时,伯努利效应将导致其周围流体的压力急速下降.当压力低于当前温度下饱和蒸气压时,就会有蒸气形态的空泡形成.当射弹速度足够高时,空泡形成包络,即形成超空泡.超空泡将射弹包裹在其中,使射弹只有少数几点与周围流体直接接触,使得射弹在超空泡中的运动阻力远小于在水中的阻力,从而为提高射弹水下运动速度提供了一个非常有效的途径[1-4].
目前关于超空泡形态的研究,一方面基于相关的经验公式进行数值仿真研究[5-7],另一方面也可根据相关原理并结合实验,解析和定量描述超空泡形态[8-10].比如李魁彬等人利用Logvinovich原理和Riabouchinsky空泡闭合模型,研究了空泡形态的一些动力学问题,并分析了首尾压差对射弹速度的影响以及射弹运动时间对完整空泡扩展时间的影响等[8].本文通过计入一阶阻尼项,修正了通常的射弹动力学方程,并解析分析了修正项对超空泡形态的影响.
1 理论分析
以射弹初始点为坐标原点建立绝对坐标系x Oy,以射弹空化器为坐标原点建立射弹相对坐标系x Oy,x轴正方向为射弹的运动方向,绝对时间轴t的相反方向为射弹相对坐标系的相对时间轴tx,如图1所示.

图1 射弹体运动图示

通常的射弹动力学方程[8]为其中,v为绝对坐标系中射弹的速度;t为绝对坐标系的时间;m为射弹的质量;ρ为水的密度;Rn为空化器的半径;Cx0为σ=0时的阻力系数;patm为大气压;H为射弹在水中的深度;g为重力加速度;pc为饱和蒸气压.式(1)可以简化为
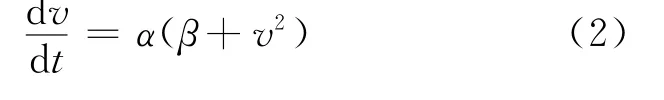

可以看出,通常的射弹动力学方程只包含速度的零阶和二阶阻尼项,考虑到更一般的运动物体所受到的阻尼与速度的零阶、一阶、二阶项均有关,为更加全面地分析射弹的运动规律,本文添加关于速度的一阶阻尼项αμv,从而得到修正的射弹动力学方程
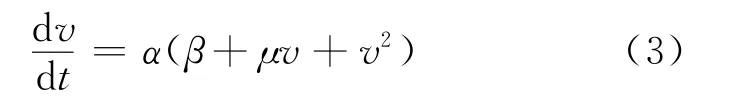
根据上述计入速度一阶阻尼项后的射弹动力学方程(3)可以发现,在不同速度条件下,速度的一阶和二阶阻尼项对射弹运动的影响是不同的.理论上可以知道,当v<μ时,速度的一阶阻尼项对射弹运动的影响是主要;反之,速度的二阶阻尼项才更为重要.同时计入速度一阶阻尼项后,射弹动力学方程依然可以解析求解,于是得到绝对坐标系下射弹速度的解析表达式
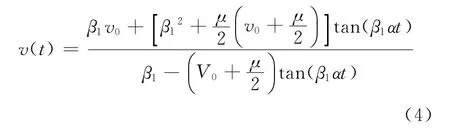
以及绝对坐标系下射弹位移的解析解
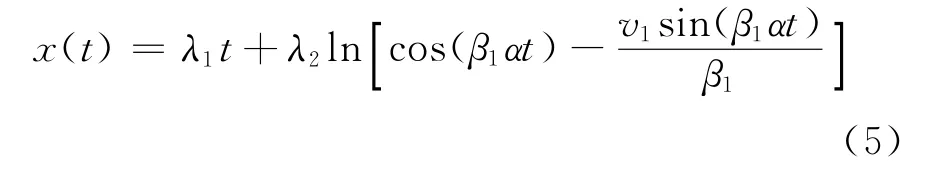
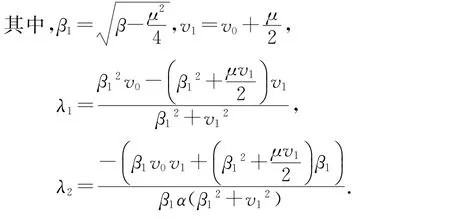
然后求解Logvinovich独立扩展方程[11]:

得到在绝对坐标系下t时刻和ξ位移处空泡的截面积S(ξ,t).这里k1=4π/A2,而A为微弱依赖于空泡数σ的系数,通常取经验值2.
再通过坐标变换式v(tx)=v(t-tx)x和x(tx)=x(t-tx)-x(t),将绝对坐标系下的速度和位移解析式变换到射弹相对坐标系,结合空泡的截面积S(ξ,t),最终得到射弹相对坐标系中空泡截面半径表达式:

2 数值仿真
根据上述一系列解析公式,将一阶阻尼系数对射弹速度、射弹位移、空泡截面半径的影响进行数值仿真,在数值计算中相关参数的取值如下:
Rn=1.00×10-3m,m=0.15kg,l=0.06m,v0=1.00×103m·s-1,patm=1.01×105Pa,pc= 2.35×103Pa,H=10m,而下面各图中不同线形的曲线对应一阶阻尼项系数μ分别取值0,45,110,200.
图2为绝对坐标系下射弹速度与时间的变化规律.可以看出,一阶阻尼项对射弹速度有着明显的影响,一阶阻尼项系数μ值越大,射弹速度减小地越快.比如当一阶阻尼项系数为200时,经过0.72s射弹速度由1.00×103m·s-1衰减为62.10m·s-1.

图2 射弹速度随时间的变化
图3显示了射弹位移与时间的变化规律.同样可以明显看出,一阶阻尼项系数μ值越大,则射弹位移增加地越慢,达到平缓段所用的时间越短.比如,当一阶阻尼项系数为200时,经过2.00s其位移为2.02×102m,此时速度更是衰减为3.70m·s-1.

图3 射弹位移随时间的变化

图4 空泡截面半径与时间的关系
图4显示出空泡截面半径随时间的变化规律.一阶阻尼项系数μ越大,则完整空泡的扩展时间越小.同时可以看出,一阶阻尼项系数μ对空泡截面半径的作用在空泡开始处的影响作用不明显,但在靠近空泡闭合处其影响作用非常明显.特别地,取绝对时刻为0.70s和一阶阻尼项系数为200,则相对时刻为6.00×10-4s时,空泡截面半径为1.00×10-3m.根据Riabouchinsky空泡闭合模型[8],此时空泡达到闭合状态,因此在该条件下完整空泡的扩展时间为6.00×10-4s.
为了更直观地观察超空泡的变化情况,图5显示出空泡截面与位移的变化关系.同时图中给出了与已有经验公式的比较,而经验公式采用Savchenko[12]提出的空泡无量纲半径公式
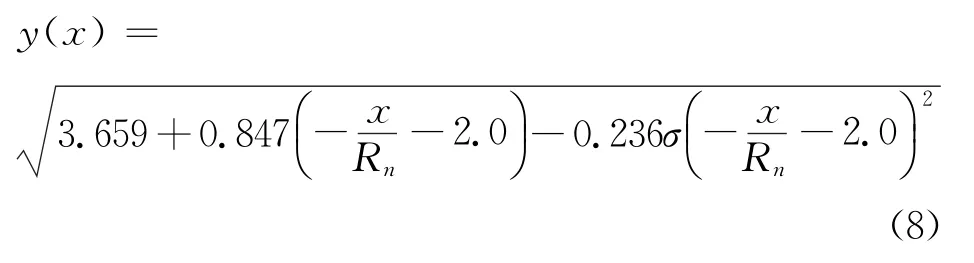
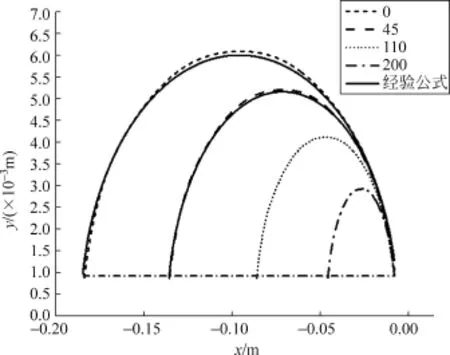
图5 绝对时刻0.7s时空泡截面半径与位移的关系
可以看出,当一阶阻尼项为零时,空泡截面半径与经验公式较为吻合.但是考虑一阶阻尼项系数μ后(比如图5中μ取45时),空泡截面半径与经验公式更为符合.并且还可看出,随着一阶阻尼项系数增大,则空泡的长度越小,最大空泡截面积越小,这样就越不利于超空泡的形成.比如,当一阶阻尼项系数为200时,经过0.70s的时间,空泡长度为3.86×10-2m,空泡截面最大半径为3.20× 10-3m,射弹速度由1.00×103m·s-1已经衰减为65.00m·s-1.
3 结语
首先通过添加一阶阻尼项对射弹动力学方程进行了修正,然后得到了修正的射弹动力学方程的射弹速度和位移的解析表达式,并结合Logvinovich方程对超空泡形态进行了数值研究.结果表明,一阶阻尼项系数对射弹运动以及空泡形态都有明显的影响.当一阶阻尼项系数越大,则射弹速度衰减地越快,完整空泡的扩展时间越短,空泡长度越小,空泡截面最大半径也越小,这样就越不利于空泡的形成.
[1]Guang Feng,Wei-qi Chen.Simulation of unsteady artificial super-cavities[J].Journal of Hydrodynamics,2010,22(5): 905-911.
[2]颜开,褚学森,许晟,等.超空泡流体动力学研究进展[J].船舶力学,2006,10(4):148-155.
[3]张学伟,张亮,王聪,等.基于Logvinovich独立膨胀原理的超空泡形态计算方法[J].兵工学报,2009,30(3):361-365.
[4]严导淦.流体力学中的总流伯努利方程[J].物理与工程,2014(4):47-53.
[5]王海斌,张嘉钟,魏英杰,等.空泡形态与典型空化器参数关系的研究——小空泡数下的发展空泡形态[J].水动力学研究与进展,2005,A辑20(2):251-257.
[6]周家胜,易文俊,王中原,等.水下射弹的空泡形态特性研究[J].弹箭与制导学报,2007,27(3):173-178.
[7]贾力平,张嘉钟,于开平,等.空化器线性与超空泡减阻效果关系研究[J].船舶工程,2006,28(2):20-23.
[8]李魁彬,王安稳,施连会,等.基于Logvinovich原理超空泡形态解析解研究[J].弹道学报,2013,25(2):103-106.
[9]袁绪龙,张宇文,刘乐华,等.水下航行体通气超空泡形态实验研究[J].应用力学学报,2004,21(3):33-37.
[10]刘玉秋,张嘉钟,于开平,等.非流线型航行体超空泡减阻的实验分析和数值模拟[J].哈尔滨工程大学学报,2006,27(3):335-338.
[11]LOGVINOVICH G V.Hydrodynamics of flow with free boundaries[M].Kiev:Naukova Dumka,1969.
[12]SAVCHENKO Y N.Experimental investigation of supercavitating motion of bodies[J].Supercavitaing Flows,2001(4):1-30.
THE MODIFIED EQUATION OF PROJECTILE MOTION AND SUPERCAVITY SHAPE
He Shengsheng1Hou Kunyuan2Liu Shiqi2Wu Minghe3Teng Baohua3
(1School of Microelectronics and Solid-State Electronics;2School of Communication&Information Engineering;3School of Physical Electronics;University of Electronic Science and Technology of China,Chengdu,Sichuan 610054)
The supercavity has a great influence on the underwater projectile high speed motion.In order to more comprehensively reflect the influence of cavity section on the underwater projectile motion and the changes of supercavity shape,this paper modifies the common equation of motion and obtains the analytical solution of speed and displacement of underwater projectiles based on Logvinovich’s principle.Then using numerical simulation,this paper studies the changes of supercavity shape during the underwater projectile motion.Analytical and numerical results show that the bigger correction factor,the faster the velocity decays,the shorter the expansion time of the complete cavity,the shorter the length of cavity,and the smaller the biggist radius of cavity section,which is adverse to the formation of cavity section.
equation of projectile motion;supercavity;equation of Logvinovich
2015-09-27
2016-02-01
何生生,男,电子科技大学微电子专业本科生.
指导老师:滕保华,男,教授,从事凝聚态物理研究和大学物理教学工作.
何生生,侯坤元,刘诗琪,等.射弹动力学方程的修正与超空泡形态[J].物理与工程,2016,26(4):96-99.

