基于影响空间的初始中心点优化K-means聚类算法

赵文冲，蔡江辉，张继福

(太原科技大学 计算机科学与技术学院，太原 030024)



基于影响空间的初始中心点优化K-means聚类算法

赵文冲，蔡江辉，张继福

(太原科技大学 计算机科学与技术学院，太原 030024)

针对K-means聚类算法依赖初始点、聚类结果受初始点的选取影响较大的缺陷，给出了一种稳定的基于影响空间的初始点优化K-means聚类算法。该算法借助了影响空间数据结构和定义的加权距离吸引因子，将特殊中心点合并为K个微簇，并对微簇中的数据点加权平均得到K个初始中心点，然后执行K-means算法；最后，理论分析和实验结果表明，该初始点优化K-means聚类算法能够有效降低噪声数据对聚类结果的影响，在聚类结果、聚类过程效率方面有较大优势。

K-means算法；影响空间；加权距离吸引因子；初始点优化

聚类作为数据挖掘的重要技术之一，是在没有任何先验知识的前提下，将给定数据集中的数据对象划分到一个一个簇中，使得簇内部对象间的距离尽可能小、信息尽可能相似，而不同簇间的对象间的距离尽可能大、信息尽可能不相似的过程[1]。

目前，国内外学者已经提出了众多聚类算法，大致可以分为以下几大类[1]：划分方法、层次方法、基于密度方法、基于网格方法以及基于模型方法。K-means[2]是一种简单的、无监督的划分聚类算法，由于具有简单易实现、通用性强、计算复杂度较低、对数据输入顺序不敏感等优势[3]，成为最受关注的最经典算法之一。与此同时，K-means算法存在许多缺陷[4]，其中最主要缺陷之一是K-means作为一种迭代算法，易收敛于局部最优解，对初始聚类中心和噪声数据特别敏感。

针对K-means算法的初始中心点选取问题，本文给出了一种基于影响空间的初始中心点优化K-means聚类算法。算法能够获得稳定的更加符合分布的初始中心点，充分降低噪声数据的影响，有效的提高了聚类质量。

1 相关工作

作为一种无监督学习方法，K-means可以为其它数据挖掘算法提供初始化、预处理等操作，因此初始中心点的选取不仅是K-means的单独问题，而应当是依托K-means的所有算法的共同问题，初始中心点的优化选取成为一项更加重要的任务。自K-means被提出，大量的初始中心点优化选取方法被提出，归纳起来，大致分为随机抽样方法、距离优化方法以及密度估计方法等三类[5]。

1.1 随机抽样方法

R-SEL算法[6]是最早的初始点选择算法之一，也是最典型利用随机抽样思想的算法之一。数据集中的每个对象成为中心点的几率等大，对于均匀分布且无噪声的情况下能够快速聚类。MacQueen等人[2]提出将数据集按任意顺序进行输入，挑选前K个输入对象为初始聚类中心的思想，改进了对输入顺序的不敏感性。但噪声数据对两种算法的聚类结果产生较大影响。

Zhu等人[7]提出了一种基于随机抽样的通过迭代计算比较当前距离与所设定的距离阈值的大小进行中心点增删的启发式求取初始聚类中心点的方法。算法一定程度上很好的提高聚类精度、减少聚类过程中迭代次数，而且减少了对噪声和输入顺序敏感性。

1.2 距离优化方法

李金宗等[8]介绍了一种最大最小距离的初始中心点优化算法，通过比较当前所选取的中心点与其它所有数据对象的最小距离的最大者获得下一个中心点，算法迭代进行，直到获得K个中心点为止。算法简便易实现，但时间消耗大成为制约该算法的一大缺陷。针对高计算量，武霞等[9]提出了一种基于最大值原则的改进算法，不仅降低了计算量，而且提供了一种并行思想策略。

Sathiya G等人[10]提出了基于原点的距离优化算法。首先计算排序各数据对象到原点的距离，并将这些距离等分成K等份，取中间点所对应的数据对象作为聚类中心点。此算法将原点作为一个参考点进行初始聚类中心点的选取，能够准确高效地处理分布均匀的数据集，但对于某些分布不均匀数据集，效果则不明显，甚至可能产生更高的时间消耗。

1.3 密度估计方法

Yang等人[11]提出一种密度估计方法选择初始聚类中心算法。算法思想是利用邻域不断寻找剩余数据集中局部密度最大的数据点作为初始中心点，并将已得到的初始中心点以及初始中心点的k邻域以及ε邻域中的数据点从数据集中去除。算法对数据输入顺序不敏感，对分布均匀数据集聚类效果明显，但由于先验条件的缺失，算法在处理分布不均匀，存在多个密度层次的数据集时，效果并不明显，很容易出现初始点集中在最稠密的小区域内，造成聚类质量的下降，迭代次数的增加等问题。

Bianchi F M等人[12]提出两种新的利用PDF进行初始点选取的算法。算法首先得到数据对象的相异度矩阵，通过设定合适的PDF对数据对象的局部密度进行估计，最后得到局部密度最大的数据对象作为初始点。同时，在大型数据集的处理上，算法设定的两种抽样方法进行数据抽样，降低了求取相异度矩阵的时间消耗。

2 初始点优化方法

2.1 相关定义

假设给定数据集为D，|D|表示数据集D中数据对象的数目，设数据对象p，q∈D.在该优化算法中，首先选取一个与距离无关的参数k，参照文献[13]-[15],进行以下相关定义.

定义1k邻域距离.p的k邻域距离kdist(p)，定义为dist(p,q)，其中q∈D，是距离p的第k个最近数据对象。

定义2k邻域点集.p的k邻域点集NNk(p)，定义为D中与对象p的距离不大于kdist(p)的所有数据对象组成的集合。

定义3 反k邻域点集.p的反k邻域点集RNNk(p)，定义为NNk中存在对象p的所有数据对象组成的集合，即RNNk(p)={q|q∈D,p∈NNk(q)}.

通过将对象的k邻域点集和反k邻域点集进行结合，我们就可以得到对象的影响空间。

定义4 影响空间.对象p的影响空间ISk(p)，定义为对象p的NNk(p)和RNNk(p)的交集，即:

ISk(p)={s|s∈NNk(p)∩RNNk(p),s∈D}

由定义1-4，可以得到对于任意数据对象r∈D，有|NNk(r)|≥k，|RNNk(r)| ≥0，|ISk(r)| ≥0.考察全局噪声数据和局部噪声数据，由于噪声数据基本处于分布比较稀疏，密度较小的区域，因此噪声数据一般孤立于非噪声数据的RNNk和ISk外，噪声数据的ISk拥有较小的数据对象个数。因此，利用影响空间对数据集进行区域划分，可以很好地降低噪声数据对全局、局部聚类的影响，提高聚类质量。

数据集D中的各个数据对象依照影响空间大小进行重新降序排列之后，得到了新的数列为V.顺序访问数据点的影响空间中的数据i，对访问过的数据i进行标记Visited(i)=1，在对V顺序访问过程中针对访问过的数据不再进行访问其影响空间。这样得到数据集D的特殊中心点集。

定义5 特殊中心点.所谓的特殊中心点集SC，定义为对V进行访问过程中，未被标记的数据点组成的集合，即：

SC={o|o∈V∩Visited(o)!=1}

定义6k共享邻域点集.数据对象p,q∈D，则p,q的k共享邻域点集SNNk(p,q)为对象p的NNk(p)与对象q的NNk(q)中共享的点集。即

SNNk(p,q)={r|r∈NNk(p) ∩NNk(q)}

定义7 加权距离吸引因子.数据对象p,q∈D，则该两数据点的加权距离吸引因子为

da(p,q)=

其中d=dist(p,q)；|SNNk(p,q)|为p，q的共享邻域内元素的数量；同样的，|ISk(p)|与|ISk(q)|分别是p和q的影响空间中的数量。

这里采用加权距离吸引因子作为数据对象间合并的因子，不仅考虑数据对象间的度量距离，同时具有如下优势：

(1)充分考虑了两个数据对象在数据集中的分布。

加权距离吸引因子两对象的共享邻域内元素的数量、每个对象的影响空间中元素的数量以及两对象间的距离平方三个方面构成。如图1所示，此为一个二维的数据集，假设图中的各标注的点的坐标为p=(2,4.9),q=(4.5,3.6),o=(3.0,4.0),r=(2.2,4.7),并设定k=4.对各标注点求NNk区域，即在图中各个圆所表示区域。通过计算得到，dist(p,o)=1.3454，dist(q,o)=1.5524，NNk(p)=6，NNk(q)=4，NNk(o)=4，研究发现，虽然p和o的NNk区域内都有点r，但r的NNk区域内只有p没有o，也就是r∈RNNk(p)但r∉RNNk(o).通过定义4及定义6，得出SNNk(p,o)=0，同样，得到SNNk(q,o)=2.则最终得到da(p,o)=0，da(q,o)>0，所以对象o与对象q更容易在同一个簇中。而事实也正好是这样，p和r所在的簇比较稠密，密度较大，而q和o所在的簇中元素分布比较稀疏，密度较小。

(2)合理考虑了局部噪声点对全局聚类的影响。

图1中，对象o相对于p和r所在的较稠密区域A来说明显地是一个局部噪声点。通过定义3、定义4以及定义7，很容易得到A对o的加权距离吸引因子为0，从而聚类过程中排除o对A的影响。

(3)由于ISk已经是按降序进行排序的，则该加权距离吸引因子符合影响空间较小的对象向影响空间较大的对象进行聚合。

图1 简单二维数据集分布

定义8 特殊中心点簇与初始中心点簇.根据加权距离吸引因子对特殊中心点进行合并，得到M个特殊中心点簇；再次对特殊中心点簇进行层次合并，最终得到K个初始中心点簇OCi，i=1,2,…,K.

定义9 加权初始中心点.对特殊中心点簇中的元素进行对应影响空间个数加权后，再平均簇内元素数据，得到加权初始中心点OWCi，i=1,2,…,K.计算公式为

2.2 算法描述

算法具体描述如下：

输入：数据集D，用户设定参数k，聚簇的个数K.

输出: K个初始中心点以及最终的K个聚簇.

/*Step1:求数据集D中的各数据对象的NNk*/

1)foreachobjectxi∈D(1≤i≤|D|)do

2)retrievingtheNNk(xi);

3)end

/*Step2:相应地，求D中各数据对象的RNNk，ISk*/

4)foreachobjectxi∈D

5)retrievingtheRNNk(xi)andISk(xi);

6)descendingallthe|ISk(xi)→V;

7)end

/*Step3:对V中数据进行访问，得到特殊中心点集PC*/

8)forallobjectsvi∈V

9)Visited(vi) = 0;

10)end

11)foreachobjectxvi∈D

12)ifVisited( xvi)==0

13)putingxviintoPC;

14)forallobjectspi∈ISk( xvi)

15)Visited(pi) =1;

16)end

17)end

18)end

/*Step4:求特殊中心点集PC中的数据间的加权距离吸引因子，并进行层次结合，得到K个初始中心簇*/

19)foreachobjectqi∈PC(1≤i≤|PC|)

//Step4.1:计算加权距离吸引因子，并排序

20)foreachobjectqj∈PC，(1≤j≤|PC|,i≠j)

21)returnningthe|SNNk(qi,qj)|;

22)calculatingtheda(qi, qj);

23)sorttingtheda(qi, qj);

24)end

//Step4.2:层次合并特殊中心点直到达到最终K个初始中心簇

25)while|PC|>K

26)accordingtotheda(qi, qj),hierarchicalclusteringuntil|PC|==K;

27)retrievingKclusters: C1, C2, …, CK;

28)end

29)end

/*Step5:对初始中心点簇中元素对象进行加权平均后得到最终的加权初始中心点*/

30)foreachobjectoi,j∈Ci,1≤i≤K,1≤j≤|Ci|

31)calculatingOWCiaccordingtothedefine8;

32)retrievingK OWC;

33)end

/*Step6:执行K-means算法

34)runningtheK-meansalgorithm.

3 实 验

本节通过实验对算法进行性能测试。实验平台配置为Intelcorei5 4570CPU，2G内存，64位操作系统的DellPC机，实验环境为eclipse，算法程序采用Java编写。实验所使用的数据全部来自于UCI数据集，表1为具体使用的实验测试数据集。同时，对原始K-means算法、文献[7]、文献[10]、文献[11]中算法以及文献[12]中的DBCRIMES2算法进行了分析比较。

表1 实验测试数据集的特征

3.1 聚类效果精度

文献[16]提供了一种评价聚类结果好坏的标准。度量标准为

其中，n为数据集数据对象个数，k为聚类的簇数，αi为聚类的簇i与已知数据集类别对应后，簇i中被正确归为相应类别的样本个数。Micro-precision的值越大，表示算法在该数据集上聚类效果越好。

表2为六种算法在各数据集上的聚类精度对比，其中，由于K-means算法、文献11算法以及DBCRIMES2算法都要随机抽取样本数据，实验中我们各取10次实验结果的平均值作为算法的聚类精度。

从表2可以看到，本文提出的优化初始中心点K-means算法充分考虑了噪声数据在数据集中的分布，选取的初始中心点均分布在局部分布密度最大的位置，聚类精度要明显优于其他5种算法。

3.2 聚类迭代次数比较

一般说来，初始中心点选取的越接近理想的中心点，聚类收敛速度越快，聚类过程效率越高。图2-图7分别为6个UCI数据集在上述6种算法下的聚类迭代次数比较。

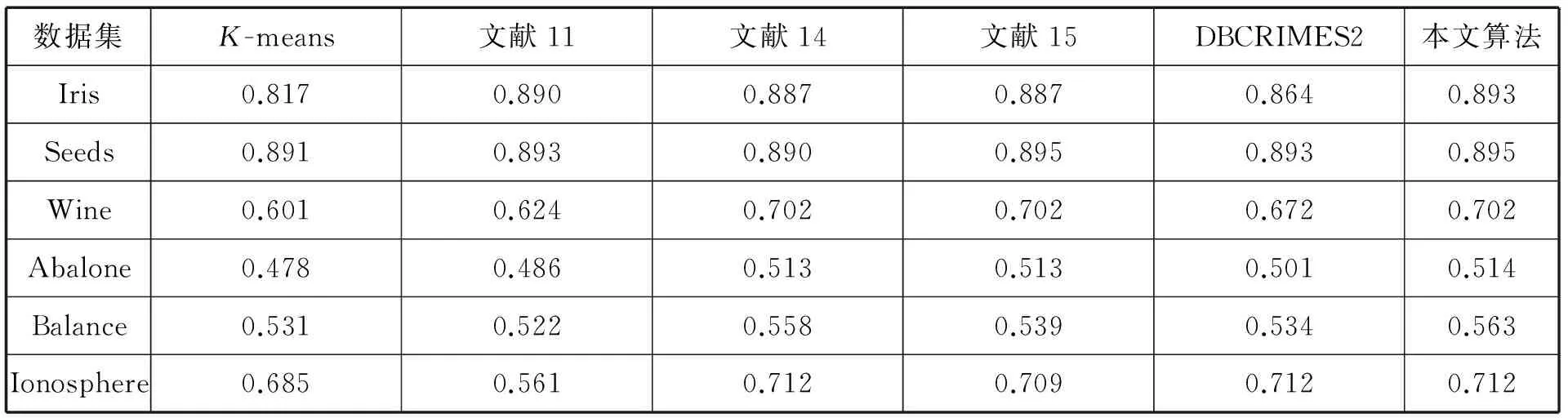
表2 各算法在不同数据集上的聚类精度对比

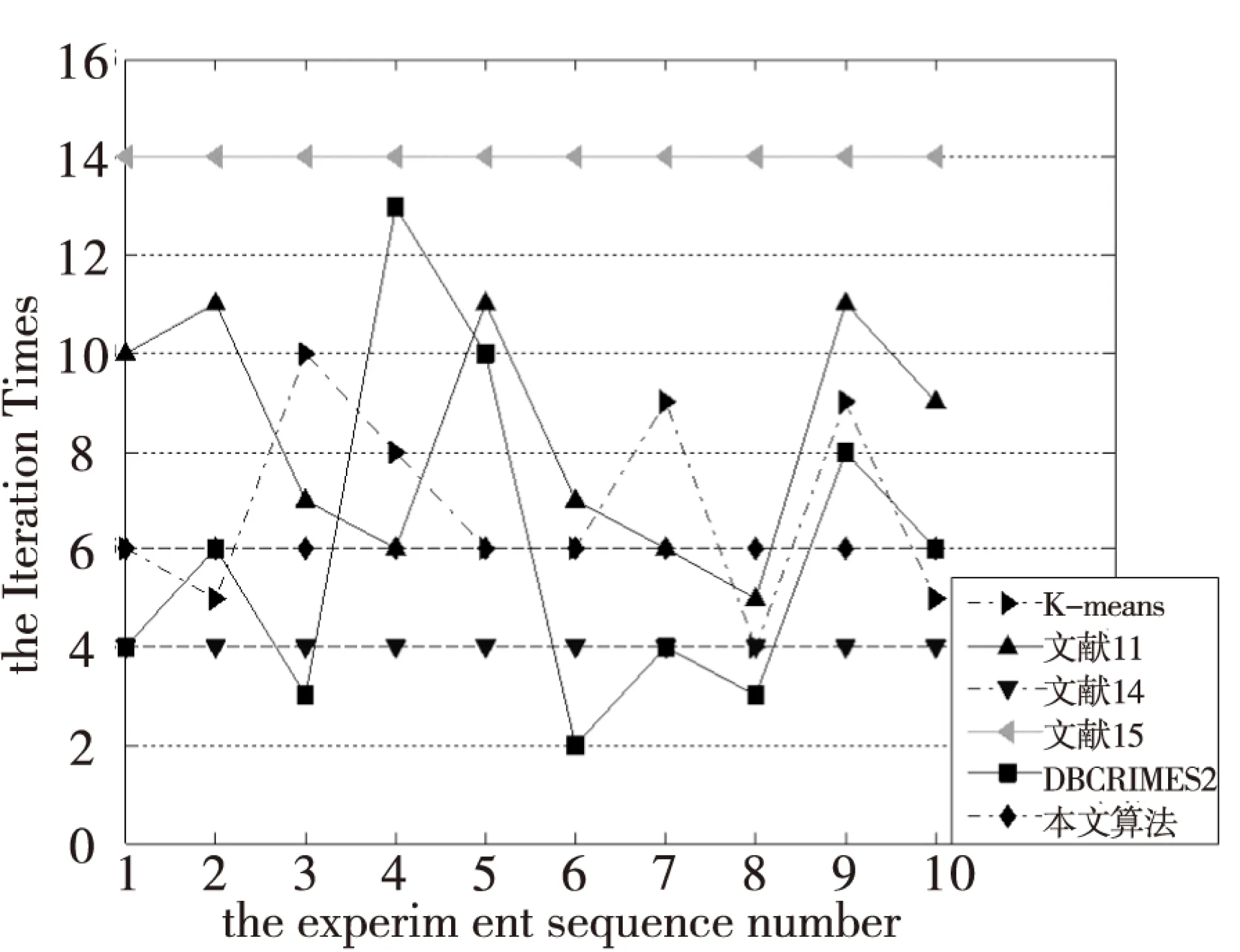
图2 各算法在Iris上的迭代次数对比

图3 各算法在Seeds上的迭代次数对比

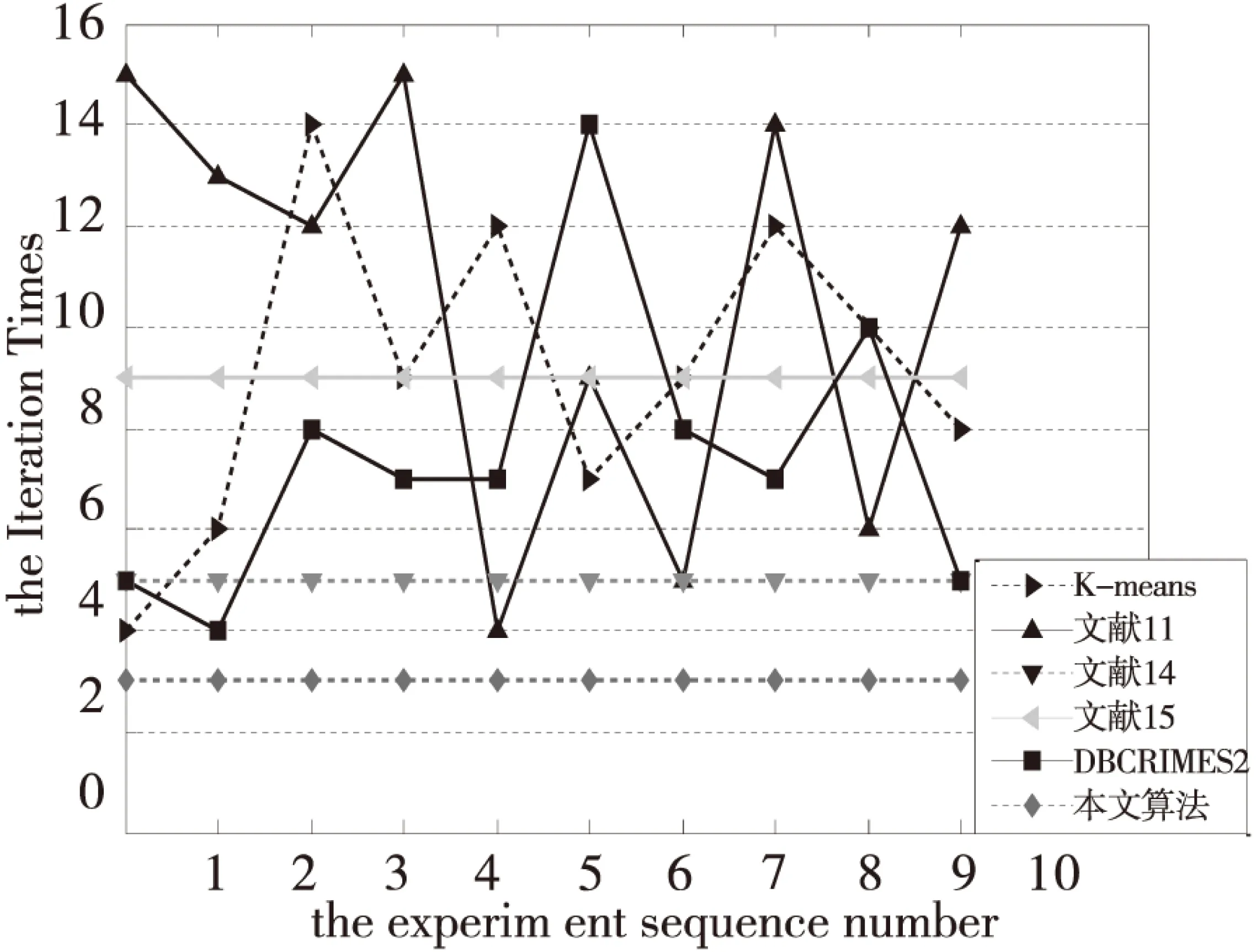
图4 各算法在Wine上的迭代次数对比

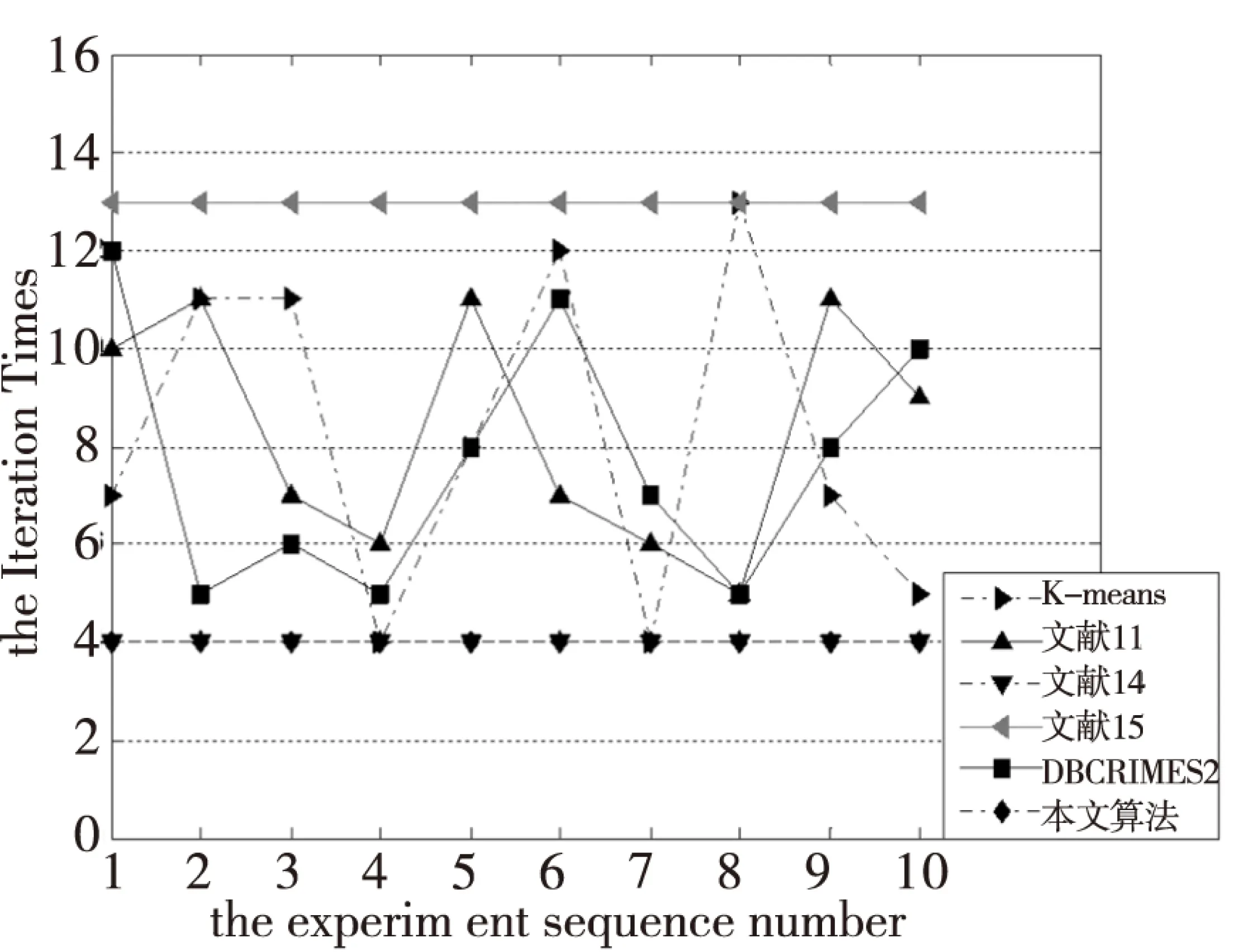
图5 各算法在Abalone上的迭代次数对比

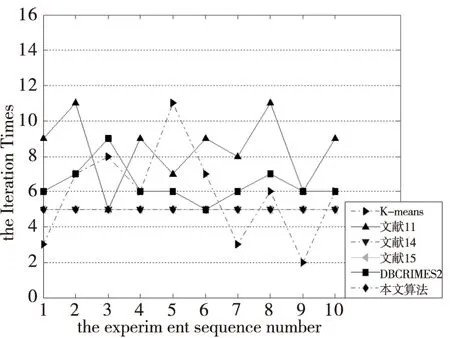
图7 各算法在Ionosphere上的迭代次数对比

比较可以得到，本文算法的聚类迭代次数比其它大多数算法迭代次数要小，表明本文算法选取的初始中心点更加接近于最终理想的中心点，在聚类过程效率方面具有较大优势。

4 结 论

针对K-means聚类算法对初始中心点依赖度高以及对噪声数据比较敏感的问题，提出一种稳定的初始点优化K-means聚类算法。采用影响空间以及共享邻域数据结构，寻找更加适合分布的初始中心点。理论分析和实验结果表明了，本文提出的初始点优化算法能够很好的削弱噪声数据对全局及局部的影响，获得更加符合分布的稳定的初始中心点，在聚类精度和聚类迭代效率方面都有相应的提高。

[1] 孙吉贵,刘杰,赵连宇. 聚类算法研究[J].软件学报,2008, 19(1): 48-61.

[2] MACQUEEN J. Some methods for classification and analysis of multivariate observations[C]// Proceedings of the fifth Berkeley symposium on mathematical statistics and probability,1967, 1(14): 281-297.

[3] CELEBI M E, KINGRAVI H A, VELA P A. A comparative study of efficient initialization methods for theK-means clustering algorithm[J]. Expert Systems with Applications, 2013, 40(1): 200-210.

[4] PENA J M, LOZANO J A, LARRANAGA P. An empirical comparison of four initialization methods for the-Means algorithm[J]. Pattern recognition letters, 1999, 20(10): 1027-1040.

[5] HE J, LAN M, TAN C L, et al. Initialization of cluster refinement algorithms: A review and comparative study[C]// Neural Networks, 2004. Proceedings. 2004 IEEE International Joint Conference on. IEEE, 2004, 1.

[6] FORGY E W. Cluster analysis of multivariate data: efficiency versus interpretability of classifications[J]. Biometrics, 1965, 21: 768-769.

[7] ZHU M, WANG W, HUANG J. Improved initial cluster center selection inK-means clustering[J]. Engineering Computations, 2014, 31(8): 1661-1667.

[8] 李金宗. 模式识别导论[M]. 北京:高等教育出版社, 1994.

[9] 武霞, 董增寿, 孟晓燕. 基于大数据平台 hadoop 的聚类算法 K 均值优化研究[J]. 太原科技大学学报, 2015, 36(2): 92-96.

[10] SATHIYA G, KAVITHA P. An Efficient EnhancedK-means Approach with Improved Initial Cluster Centers[J]. Middle-East Journal of Scientific Research, 2014, 20(1): 100-107.

[11] YANG S Z, LUO S W. A novel algorithm for initializing clustering centers[C]// Machine Learning and Cybernetics, 2005. Proceedings of 2005 International Conference on. IEEE, 2005(9): 5579-5583.

[12] BIANCHI F M, LIVI L, RIZZI A. Two density-basedK-means initialization algorithms for non-metric data clustering[J]. Pattern Analysis and Applications, 2014: 1-19.

[13] BREUNING M M, KRIEGEL H P, Ng R T, et al. LOF: identifying density-based local outliers[C]. ACM Sigmod Record. ACM, 2000, 29(2): 93-104.

[14] JIN W, TUNG A K H, HAN J, et al. Ranking outliers using symmetric neighborhood relationship[J]. Advances in Knowledge Discovery and Data Mining. Springer Berlin Heidelberg, 2006: 577-593.

[15] JARVIS R A, PATRICK E A. Clustering using a similarity measure based on shared near neighbors[J]. Computers, IEEE Transactions on, 1973, 100(11): 1025-1034.

[16] MODHA D S, SPANGLER W S. Feature weighting inK-means clustering[J]. Machine learning, 2003, 52(3): 217-237.

An OptimizationK-means Clustering Algorithm of Initial Center Objects Based on Influence Space

ZHAO Wen-chong, CAI Jiang-hui, ZHANG Ji-fu

(School ofComputer Science and Technology, Taiyuan University of Science and Technology, Taiyuan 030024, China)

In view of the shortcomings thatK-means clustering algorithm depends on the initial data objects and the clustering results are greatly influenced by the selection of initial data objects, this paper proposes a stable optimization algorithm about initial data objects chosen inK-means algorithm based on influence space. Firstly, algorithm obtains several special center points to K tiny clusters with the help of influence space data structure and a weighed distance attraction factor is defined. And K initial data objects are obtained by weighed and meaning in K tiny clusters. Then, theK-means algorithm is run on given data set. Theoretical analysis and experimental results show that the new algorithm can lower the effect of noise data objects for the clustering results effectively; meanwhile, there is a great advantage on the clustering results and the processing iteration times.

：K-means clustering algorithm, influence space, weighed distance attraction factor, initial data objects optimization

2016-01-05

国家自然科学基金(41372349)，山西省社会发展攻关项目(20140313023-2)；山西省高校优秀青年学术带头人项目。

赵文冲(1989-)，男，硕士研究生，研究方向为数据挖掘与知识工程；通信作者：蔡江辉教授，E-mail:supercooling@qq.com

1673-2057(2016)05-0347-07

TP391

A

10.3969/j.issn.1673-2057.2016.04.003