基于WAMS暂态稳定预测的发电机失步保护的协调控制
基于WAMS暂态稳定预测的发电机失步保护的协调控制

发电机失步保护是电网第三道防线的重要组成部分,特别是在组机大型化发展的今天,发电机失步保护动作与否对电网的安全稳定性影响越来越大。而以往的发电机失步保护研究只关注于发电机本身,缺乏对机组与电网协调性的研究。针对这种情况,提出基于广域相量测量系统(WAMS的)轨迹超时预测技术的可以提前预测发电机失步运动走向,可以及时切除必然会失步的大型机组或者延长切除时间将经过一段时间失步后会被电网拉回同步的机组。当电网处理临界状态时第三道防线将从电网安全稳定的角度出发,有选择性的切除机组(电网),避免出现美国8.14大停电那样的事故。
超高压电网的建设及大型发电机组的投入使电网系统电抗减小,系统若发生振荡,振荡中心一般会在落在发电机机端,对发电机特别是单元接线的大型机组的安全产生很大的危害,因此对发电机进行失步预测是很有必要的。但是目前国内外的失步保护参数为静态设置,保护参数不能随网络拓扑结构的变化作相应的调整;另一方面失步保护装置只能从局部的角度判断发电机是否会失步,没有考虑到电网的作用,没有考虑到已失步机组是否会被电网拉回同步。功角是否越限是判断发电机失步的主要标志。广域相量测量系统(WAMS)的发展,使系统受扰后功角轨迹预测与系统暂态稳定预测成为可能。暂态不稳定实时识别是为了阻止失步的发生,WAMS采集到的信息通过网络传输就会存在遗失与延时的风险,能超实时预测发电机的运动轨迹就实现百分百为WAMS的发电机失步预测及保护提供必要的系统状态信息。本文提出的基于WAMS暂态稳定预测的发电机失步保护的协调控制方法能从整个电网的稳定运行出发,在系统失稳前发出指令,切除多余能量以维持系统稳定。实现电网侧失步保护与发电机失步保护相协调。
微分动力系统的自记忆预测算法
文献[4,5]给出的预测法是“经验型”方法,没有从理论上给出深入的分析且给出的预测方法计算结果精确性太差;文献利用神经网络预测轨迹,其缺点是难以获取训练样本,而且训练过程相对艰难。基于发电机运动方程的三个状态量的滚动自记忆预测公式,考虑历史测量数据及其高阶变化量对未来的影响,具有很高的预测精度和良好的稳定性,并且能够有效预测较长的时间。发电机转子运动方程及其分析多机电力系统同步参考坐标下的转子运动方程为:

δi发电机i 的转子角/rad;∆ωi发电机i的转子角速度/ p.u.;Mi发电机i 的惯性时间常数/秒;Pmi机械输入功率/p.u.;Pei电磁输出功率/p.u.;Di阻尼因子/p.u.。∆Pi=Pmi-Pei为不平衡功率,式(1)中的、∆ωi和∆Pi是可以实时测量的,其中δi二阶连续可微,∆ωi一阶连续可微,∆Pi代表了角加速度,属于高阶量,在系统发生离散操作时可以突变,但其在各次离散操作间保持连续;并且功角、角速度、角加速度之间遵循动力学关系。总之,电力系统的运动方程是一个非线性动力学方程。计及发电机的励磁调节器和调速器后,∆Pi不再是正弦曲线,其变化情况比较复杂。
自记忆轨迹预测算法
自记忆预测通过引入记忆函数,能够计及历史信息的影响,具有较高的精度和稳定性。它适用于具有形如下式的微分动力系统:

其离散表达形式为:

p 为预测时刻之前的采样点数,βi可通过最小二乘法辨识获得。δ对应x ,ω0∆ω对应F( x,t),综合考虑预测的快速性和准确性,可以取三阶形式:
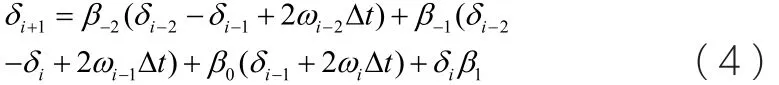
对于电力系统,(4)中与F( x,t)对应的ω0∆ω只能获得当前时刻及之前时刻的测量值,下一时刻的ω0∆ω未知,且不能准确计算,这样仅能预测下一时刻的功角δi+1。为使自记忆应用到电力系统时能进行多步预测,有必要先对ω0∆ω进行预测。使用正弦三角函数对角速度进行拟合:
∆ω=ωc(t)+λ1t(t)sin(t)+λ2t(t)cos(t )。不平衡功率的可由式子∆P=Pc( t)+λ1t(t)sin(δ)+λ2t(t )cos(δ)拟合。其中的Pc( t),λ1t(t),λ2t(t )为待辨识的时变参数。就某一确定时刻的系统运行状态而言,只要系统不遇到大的扰动,这个参数在短时间内可以作为常数处理,这时用最小二乘法辨识一次参数,之后认为它们保持恒定。
从发电机的功角轨迹图能直接判定系统是否稳定,但是不能读出系统的稳定裕度,不能将发电机的暂态稳定裕度给出一个定量的数值用于临界状态时的电力系统紧急控中。
基于轨迹预测的暂稳控制方法
系统功角失稳是因为各个发电机组无法保持同步,若能使得系统保持同步,则系统就能恢复稳定。假设系统功角失稳模式为两群失稳,则机组可以分为临界机群和其余机群,两机群之间角速度不同,则两机群之间必然有一个暂态动能差额,如果通过切除领先机群的机组来消除两机群之间的暂态动能差额,使得两机群之间的角速度差为零,则系统能够恢复同步。
基于EEAC的多余动能确定方法
利于扩展等面积定则(EEAC)原理,可以得到发电机群的惯量中心(CCCOI)在单机无穷大系统中的空间时变映像,这个映像具有映射前多机系统稳定性的所有信息。因此计算出这个映像是否稳定就得出了原多机系统是否稳定。
假设通过轨迹的稳定性预测判别出系统失稳的时刻为Te,通过切机,将判别失稳时刻Te的多余动能切除掉,就能消除临界机群与系统惯量中心的角速度差,使得系统重新恢复稳定。

因此,只要切除一定发电机,使得这部分暂态动能EK,e为零,则系统就能够恢复稳定。
在系统判别失稳时刻Te第i台发电机相对于其余机群(A)惯性中心的暂态动能为:
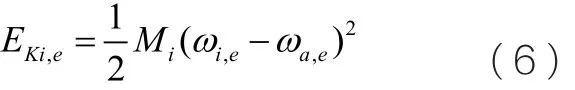
其中,ωi,e为Te时刻第i台发电机的角速度,ωa,e为Te时刻其余机群惯量中心的角速度。则该动能EKi,e即为切除该发电机时,系统多余动能EK,e所减少的值。当初始切机控制量EK确定后,可取总容量大于EK且最接近于EK的发电机作为切机量。
基于相图凸凹性稳定性判断
从单机无穷大系统空间中的时变映像可以计算出需要切除的单机无穷大系统的多余动能。为确保等值后,切机量必须计算正确,需对切机后系统的稳定性进行再次预测。文献[7,8]提出应用相图凹凸性来单机无穷大系统的稳定性,这种方法不受运行时刻网络的结构、系统参数和模型影响,并通过仿真验证该方法的有效性。
不返回点(NRP)就是相轨迹出现凸特性的点。相轨迹平面上的NRP映射到实质系统中就是机组受扰动后实际的运动轨迹。用相轨迹平面上NRP点切线斜率的正、负来作为系统是否能恢复稳定的判定依据。NRP的离散本达式为:

若∆k( i )>0,则代表系统则稳定;若∆k( i )<0,则代表系统将会失去稳定。具体流程图如图1。
仿真验证
以某省实际电网为例进行仿真验证,该省电网包含114台有效发电机。假设电力系统分析综合程序PSASP的仿真结果为WAMS的实测信息,仿真步长取10ms。
某省实际电网,在母线A与母线B之间的500kV双回线路中的一回线上0秒发生三相短路故障,并在0.13秒切除故障线路。基于预测轨迹的不稳定性判据在0.4s的时候判别出系统将要失稳。未应用本文提出的控制方法,发电机功角曲线如图25所示。假设0.55s时切机动作完成,采取控制措施切除后的系统功角曲线图3所示。
从图2图3中可以看出,本文提出的基于AMS暂态稳定预测的发电机失步保护的协调控制方法能从整个电网的稳定运行出发,在系统失稳前发出指令,切除多余能量以维持系统稳定。

图1 基于WAMS暂态稳定预测的发电机失步保护的协调控制流程图
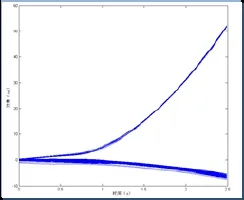
图2 无控制措施时的功角曲线图

图3 有控制措施时的功角曲线图
结语
本文针对传统发电机失步保护装置的局限性,给出了一种基于WAMS暂态稳定预测的发电机失步保护的协调控制方法。应用自记忆预测轨迹的判别方法,考虑电力系统的动力学特性,从动力学角度描述了功角的变化趋势,快速识别出系统的稳定性。并应用EEAC理论计算系统多余能量即合适的切机量。切机后系统拓朴结构会随之发生改变,采用不受网络拓朴结构影响的相轨迹凹凸性判别理论预测切机后系统的稳定状况并对切机量及时调整,提高整个系统的安全稳定水平。
10.3969/j.issn.1001- 8972.2016.21.022

