中国人民银行县支行履职动力问题研究

王浩军+王在荣

[摘要]文章运用进化博弈中的复制动态模型对中国人民银行县支行提高履职动力的发展轨迹进行模拟与分析，并得出结论：一是完善的激励机制和补偿机制是县支行提高履职效率的主要动力来源；二是在对有作为的县支行给予利益保障的同时，适当的压力将会对不想作为的县支行产生一定动力效果；三是政策支持与丰富的经验借鉴是县支行提高履职效率不可缺少的动力源泉。

[关键词]中国人民银行县支行；履职动力；进化博弈；复制动态

[DOI]1013939/jcnkizgsc201637095

1引言

中国人民银行县支行设立至今，职能不断完善，但仍存在动力不足、效率低下等问题。主要体现在三方面：一是执行货币政策方面，加强执行货币政策手段缺乏；深度调研及丰富调研方式单一；二是维护金融稳定方面，法规制度不完善，金融稳定工作定位不明确，县域金融稳定联系机制不完善；三是提供金融服务方面，提供金融服务的重要性未得到广泛认同，提供金融服务的水平有限，专业技术人员缺乏，业务技能不高。

2中国人民银行县支行履职动力的进化博弈分析21理论前提

本文的讨论是在博弈主体均为有限理性的基础上进行的。由于人民银行县支行数量多，加上相互间距离远，信息传递不及时等因素，进化博弈中的“复制动态”机制适用于人民银行县支行群体中随机配对的重复博弈。

22假设条件

第一，本文研究的履职动力问题主要是以县支行提高履职效率的动力问题为主；第二，人民银行县支行对提高履职效率的行为分为“提高”与“保持”两类；第三，从人民银行县支行中随机抽取两个单位来进行博弈，记为县支行A和县支行B。

23复制动态进化博弈模型的构建

县支行提高履职效率能否成功，考虑的因素有提高履职效率方案的合理度r，r取决于借鉴经验，可以用参与提高履职效率的县支行数量q来量化借鉴经验。除了r，影响县支行提高履职效率的因素还包括国家政策，以及县支行上级行及总行对其改革的支持度s。通常r与q呈正相关。

设县支行提高履职效率成功可以获得的收益为M，提高履职效率需要付出的成本为C。假设博弈双方县支行A和县支行B中只有一方提高履职效率时，成功的概率为P（1），双方都提高履职效率时，成功的概率为P（2）。在之前的叙述中可以知道，双方都进行“提高”行为比只有一方进行“提高”行为的q要大，因此，P（2）>P（1）。博弈双方只有一方提高履职效率，而另一方保持原履职效率，若“提高”方的成功概率为P（1），则后者的成功概率为1-P（1）。如果博弈双方都选择保持原履职效率，则获得的收益M与付出的成本C均为0。

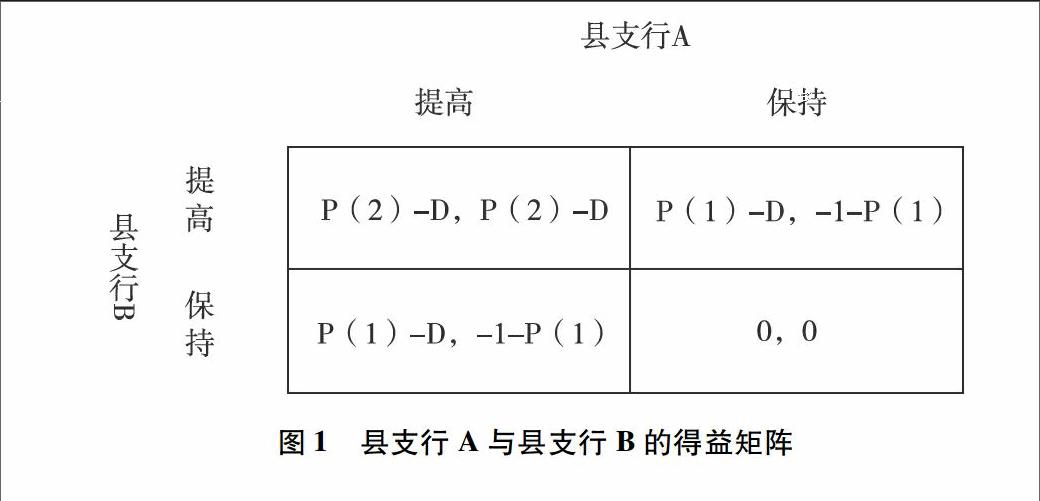
图1县支行A与县支行B的得益矩阵

县支行A与县支行B的得益矩阵如图1所示：在矩阵中，D=C/M，D指县支行提高履职效率所付出的成本与获得的收益之间的比例。由之前假定得出P（2）>P（1），所以P（2）-D>P（1）-D。在有限理性的前提下，县支行A与县支行B在开始时不一定可以准确找到最优策略，在重复博弈的过程中，它们会逐步寻求最佳策略。

24复制动态和进化稳定策略ESS

设县支行中，采取提高履职效率行为的县支行所占比例为X，采取保持原履职效率的县支行所占比例为1-X，根据2×2对称博弈的规律，则采取“提高”策略的期望得益U1和采取“保持”策略的期望得益U2以及群体中平均期望得益U-分别是：

根据上述得益得到复制动态方程：

在式（4）中，dXdt表示采取提高履职效率行为的县支行的比例随时间的动态变化速度。一般可以将上述复制动态方程简记为dXdt=F（X），F（X）=0，即可解得所有可能的复制动态稳定状态。

=0，解得=0是三个可能的稳定状态。

由进化稳定策略的性质可知，进化稳定策略（ESS）的稳定状态必须对微小扰动具有稳定性。即作为进化稳定策略的点，除了本身必须是均衡状态以外，还必须满足这样的条件，就是如果某些博弈方由于偶然的错误偏离了它们，复制动态仍然会使X回到X*。在数学表达中，这相当于要求当干扰使X出现低于的情况时，dXdt=F（X）必须大于0，当干扰使得X出现高于的情况时，dXdt=F（X）必须小于0，也就是在这些稳定状态处F（X）的导数（即切线斜率）F′（）必须小于0。

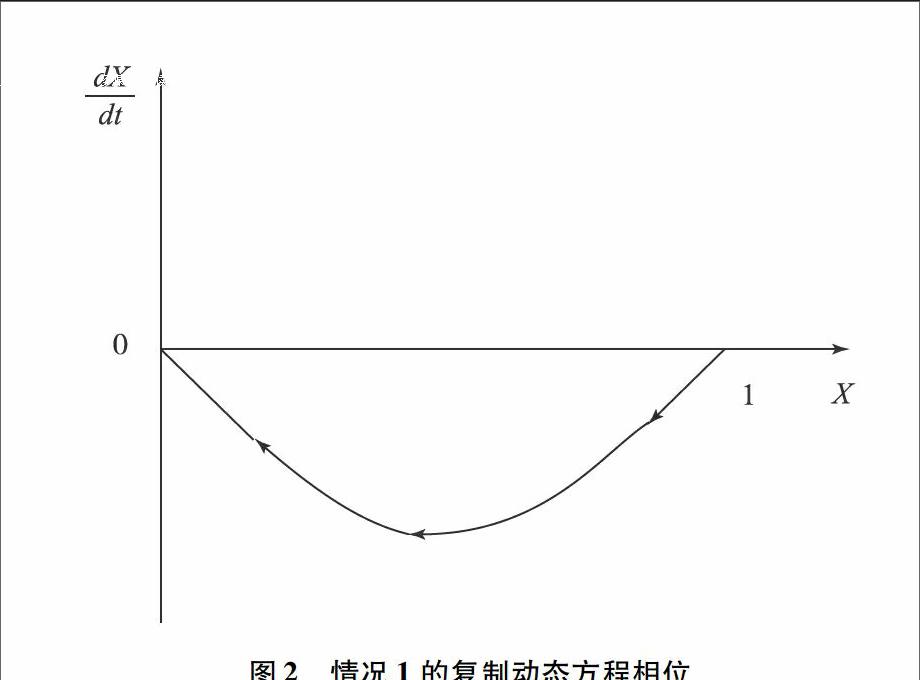
情况1：当[P（1）-D]/[1-P（2）]<0时，可得：

M·P（1）

式（5）表示县支行中博弈一方单独采取“提高”行为的收益将低于其成本，此时复制动态方程的不动点有X*1=1和X*3=0。该情况下复制动态方程的相位图如图2所示：

图2情况1的复制动态方程相位

根据相位图可以看出，在X=0处F（X）的切线斜率小于0，在X=1处F（X）的切线斜率大于0，因而此时复制动态的唯一稳定的均衡点就是X*3=0，也就是（保持，保持）是上述博弈模型的进化稳定策略ESS。

情况2：当0<[P（1）-D]/[1-P（2）]<1时，可得：

M·P（1）>C且M·P（2）-C

式（6）中M·P（1）>C表示博弈一方单独采取“提高”行为的收益大于成本，而M·P（2）-C

从相位图中可以看出，只有在的切线斜率小于0，因此是复制动态的唯一均衡点，此时（提高，保持）将是上述博弈模型的进化稳定策略ESS。在此情况下，当X=0时，即所有县支行都采取“保持”行为的状态下，如若有少数县支行采取“提高”行为，因为一方单独“提高”的收益大于成本，所以随着获益增多，采取“提高”行为的县支行数量将不断增加，直到采取“提高”行为的县支行比例达到[P（1）-D]/[1-P（2）]。但是如果大于该比例了，因为“提高”不一定成功，若“提高”结果为失败，则“保持”显得更加稳妥。因此，“保持”行为将会在所有县支行中扩散，最终将回到X2=[P（1）-D]/[1-P（2）]的均衡状态。

情

根据相位图可以看出，在X=0处F（X）的切线斜率大于0，在X=1处F（X）的切线斜率小于0，因此，复制动态唯一稳定的均衡点为X*1=1，即（提高，提高）将是上述博弈模型的进化稳定策略ESS。

3结论及对策建议

第一，完善的激励机制和补偿机制是县支行增强履职动力，提高履职效率的主要手段。如上述博弈模型的情况1所示，即使有少数人民银行县支行先行尝试“提高”，在经历多次博弈之后，（保持，保持）策略成为了县支行关于增强履职动力问题上的进化稳定策略。由上述博弈模型中式（5）与式（6）及其复制动态可以得出，县支行参与提高履职效率行为的前提条件是一方单独“提高”或先“提高”所获得的收益要大于其成本。总行及上级行对尝试增强履职动力，提高履职效率的县支行应当给予充分肯定和支持。

第二，在对有作为的县支行给予利益保障的同时，适当的压力将会对不想作为的县支行产生一定动力推动效果。结合上述博弈模型中情况2可以看出，人民银行县支行在尝试增强履职动力，提高履职效率的过程中，可能会遇到一些未知的困难使得“提高”行为无法继续进行下去，此时（提高，保持）策略成为人民银行县支行增强履职动力，提高履职效率的进化稳定策略。由上述博弈模型中的式（6）和式（7）显示出若县支行A和县支行B中的一方尝试“提高”，另一方选择跟随“提高”的净收益比选择“保持”的净收益要大。

第三，政策支持与丰富的经验借鉴将是县支行增强履职动力，提高履职效率不可缺少的因素。在D相对稳定的情况下，即采取“提高”行为所获得的收益和付出的成本之比相对稳定时，由于q与r、s正相关，要使得“提高”策略作为县支行的均衡选择，上级行和总行可以增大s，即对采取“提高”行为的县支行给予充分支持。

参考文献：

[1]谢识予经济博弈论[M].2版上海：复旦大学出版社，2002

[2]张华关于人民银行县支行在发展县域经济中职能定位的思考——温州地区县支行实证分析[D].上海：复旦大学，2009

[3]张桥云人民银行县支行职能定位的探讨[D].昆明：云南财经大学，2009

[4]李思敏，万里滨中央银行县支行机构改革路径的优化选择[J].南方金融，2006（7）：16-19

[5]石志红，王其伟人民银行县支行高效履职面临的困难与对策[J].西部金融，2010（4）：48-49