挖掘课本资源,演绎变式精彩
——加权平均数的延伸与拓展
苏红芬
挖掘课本资源,演绎变式精彩
——加权平均数的延伸与拓展
苏红芬
在小学阶段同学们就已经学过计算一组数据的平均数的方法.设有n个数据x1,x2,…,xn,我们将叫做这n个数据的算术平均数,简称平均数.平均数通常可以用来表示一组数据的“集中趋势”.而有些实际问题用算术平均数不能解决问题,一组数据的平均数,不仅与这组数据中各个数据的值有关,而且与各个数据的“重要程度”有关,我们把衡量各个数据“重要程度”的数值叫做权,设有n个数据x1,x2,…,xn,各个数据对应的权w1, w2,…,wn,我们将叫做这n个数据的加权平均数.在实际的学习过程中,同学们对“权”的含义以及“权”对结果的影响理解起来往往比较困难,下面我们将结合苏科版九年级上册3.1平均数第二课时的例题进行深入探究.
一、还原例题,变式应用
问题11:为了解某市九年级学生开展“综合与实践”活动的情况,抽样调查了该市200名九年级学生上学期参加“综合与实践”活动的天数,并根据调查所得的数据绘制条形统计图如下:

求这200名学生参加“综合与实践”活动的平均天数.
【解析】这200名学生参加“综合与实践”活动的平均天数,不仅与参加活动的天数有关,还与相应的人数有关,人数10、30、60、50、50分别是天数2、3、4、5、6的权,因此正确的算4.5(天).
【变式1】为了解某小区居民的日用电情况,居住在该小区的一名同学随机抽查了15户家庭的日用电量,结果如下表:
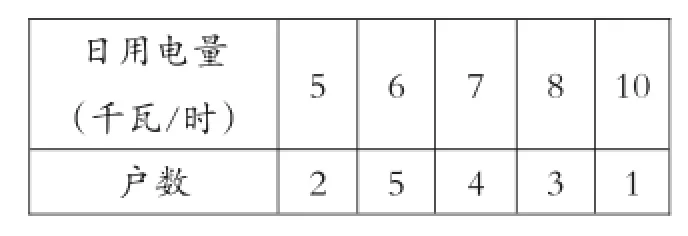
日用电量(千瓦/时)户数6 5 5 2 7 4 8 3 10 1
求平均日用电量.
【解析】平均日用电量不仅与日用电量有关,还与户数有关,户数2、5、4、3、1分别是日用电量5、6、7、8、10的权,因此(千瓦/时).
【变式2】为了考察东昌府区13岁男生的平均身高,从中随机抽取了240人,测得他们的身高(单位:厘米)如下表所示:

140 141 142 143 144 145 146 147 148身高人数2 10 16 56 70 56 20 8 2
计算这个样本的平均数(精确到1厘米),并由此估算出全区13岁男孩的平均身高.
【解析】这个样本的平均数不仅与身高有关,还与人数有关,人数2、10、16、56、70、56、20、8、2分别是身高140、141、142、143、144、145、146、147、148的权,因此-x=144(厘米).
问题2:某电视台要招聘1名记者,甲、乙、丙三人应聘参加了3项素质测试,成绩如下(单位:分):
(1)如果采访写作、计算机操作和创意设计的成绩按5∶2∶3计算,那么三个人的素质测试平均成绩各为多少?
(2)如果采访写作、计算机操作和创意设计成绩按4∶2∶4计算,那么哪个人的素质测试平均成绩高?

甲乙丙采访写作70 90 60计算机操作60 75 84创意设计86 51 78
【解析】采访写作、计算机操作、创意设计的重要程度不一样,(1)中5、2、3分别是这三项成绩的权,因此
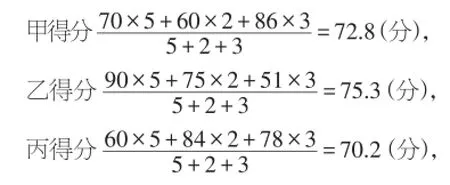
所以选乙.
(2)中4、2、4分别是这三项成绩的权,因此
所以选甲.
通过(1)与(2)的辨析,再次感受到了权不同,数据的重要程度不同,结果也就不同.
【变式1】某报社在面试职员招聘中,甲、
乙、丙三人的各项得分如下表:
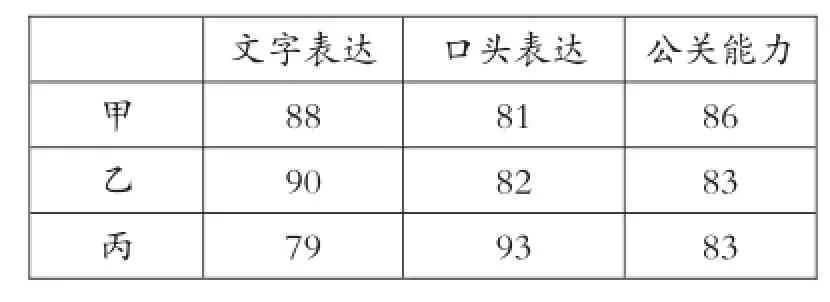
丙关能力86 83 83 79 93
(1)如果根据三项得分的平均数从高到低确定名次,那么三人的排名顺序怎样?
(2)如果你是主考官,报社需要招聘一名记者,该如何设计三个项目的比重?谁是最佳人选?
(3)如果你是主考官,报社需要招聘一名编辑,又该如何调整三个项目的比重?谁又是最佳人选?
甲的平均分

乙的平均分
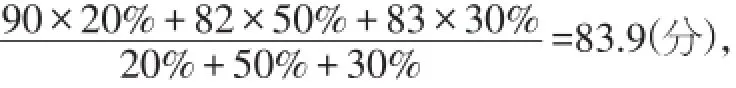
丙的平均分
让学生在自主学习的过程中学会和同学相互合作、学会分析问题,让所有学生都可以快乐的学习。但根据现阶段的学习模式而言,知识主要是靠教师和书本来传播的,效率低、方法单一,不利于学生的自主学习。将现代信息技术带到课堂,可以扩大学生的学习空间,使他们能高效快速地掌握更多的知识。例如,当教师在讲解“地球表面”一课时,教师可以带学生去机房,通过图片、视频等方式能使学生主动去接受这些知识,从而提高教学质量。

所以选丙.
如果报社要招聘的是一名编辑,那么对文字表达要求比较高,口头表达和公关能力要求相对较弱,所以可以设计成文字表达、口头表达、公关能力分别占50%、25%、25%,于是可以计算出:
甲的平均分

乙的平均分

丙的平均分
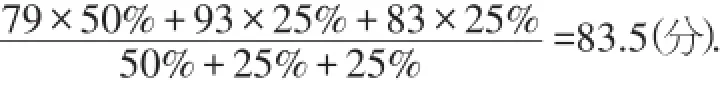
所以选乙.通过刚才三次计算的结果,发现每一次的结果都发生了变化,权越大,对结果影响越大.那么在做决策时如何利用好“权”,可以按照各个项目的重要程度来确定比重,如果一个项目很重要,则分配“权”要多一些,“权”对决策起重要作用.
【变式2】某球队欲挑选一名篮球新秀,现有3名候选人,教练对其进行3项素质测试,测试结果如下表所示.

(注:为了方便计算,每次篮板或助攻计1分).
如果你是教练,你将以怎样的方式选择新秀?写出你的方法并通过计算说明.
【解析】前锋:对队员的投篮能力要求较高,篮板和助攻次重要.中锋:对队员的篮板能力要求较高,投篮和助攻次重要.后卫:对队员的助攻能力要求较高,投篮和篮板次重要.作为教练,你想选择的球员是哪个位置的?
(1)如果想选择的是前锋.投篮所占的比重要高一些,所以可以设计成投篮、篮板、助攻按6∶2∶2计算.
所以选乙.
(2)如果想选择的是中锋.篮板所占的比重要高一些,所以可以设计成投篮、篮板、助攻按2∶6∶2计算.
甲的得分=14.2(分),
乙的得分=14.4(分),
丙的得分=16.2(分).
所以选丙.
(3)如果想选择的是后卫.助攻所占的比重要高一些,所以可以设计成投篮、篮板、助攻按2∶2∶6计算.
甲的得分=14.2(分),
乙的得分=9.2(分),
丙的得分=11(分).
所以选甲.
同学们通过解决这样的实际问题,会进一步体会加权平均数对于计算平均数的重要性,同时开放性问题将会给同学们提供更大的思维空间,培养数学思维能力和方法,更进一步了解“权”对于各个数据的重要程度.
(作者单位:江苏省常州市武进区湖塘实验中学)

