基于SVM的信号解调算法*
滕晓云,徐 俊,陈德明
(中国卫星海上测控部,江苏 江阴 214431)
基于SVM的信号解调算法*
滕晓云**,徐俊,陈德明
(中国卫星海上测控部,江苏 江阴 214431)
在小样本、低信噪比条件下,同步参数估计会存在较大误差,从而导致信号解调性能的降低。为了解决该问题,将信号解调看成有限长度采样样本的学习问题,并利用支持向量机(SVM)良好的学习性能,在存在同步误差的条件下,通过提高判决端的处理能力来改善系统的接收性能,提出了基于SVM的信号解调算法。在Matlab环境下,对提出算法在精准同步、残存同步误差、高斯白噪声和高斯色噪声等情况进行了计算机仿真,结果表明,相比于匹配滤波器算法,基于SVM的信号解调算法能较好地克服定时误差和相位误差以及色噪声对解调性能的影响。
信号解调;支持向量机;相位误差;定时误差
1 引 言
为提高接收性能,通信系统一般采用相干接收的处理方式。无线信道的随机性以及接收信号中存在的相位、定时误差等参数的未知性,给相干接收的实现带来了很大的难度。传统的通信信号解调过程分为同步和解调两个基本环节,即首先进行同步参数估计,然后在假定同步参数已被精确估计的前提下进行信号解调。传统的通信系统通常采用各种类型的反馈环路为接收机提供实时的载波提取和跟踪以实现相干接收。但是,由于反馈环路的锁定需要一定的时间,对接收信号载波的动态跟踪也需要一定数量的数据以提供误差信息。而对于某些通信系统而言,数据信息的传输是不连续的,因此接收机很难通过反馈环路实现载波同步和定时同步。应用前向参数估计算法是解决通信系统中同步参数估计问题的主要手段[1-3],而受限于参数估计算法的实现复杂度和估计精度,同步参数估计难免存在较大误差,传统的解调处理不考虑残留的同步误差而直接进行信号解调,这必然导致解调性能的降低。因此,如何提升小样本、低信噪比条件下的信号解调性能一直是通信信号处理的难点之一。本文拟探讨在存在同步误差的条件下,如何通过提高判决端的处理能力来改善系统的接收性能。
将信号解调转化为针对带有确定但未知的相位和定时误差等参数的有限长度采样样本的学习问题,并利用支持向量机(Support Vector Machine,SVM)优良的泛化性能解决,本文研究了基于SVM的信号解调算法。SVM采用结构风险最小化(Structure Risk Minimization,SRM)准则[3],较好地解决了小样本、非线性和局部极小值等实际问题,并且由于它的解只与支持向量有关,可以很大程度上节省计算复杂度。鉴于上述优点,SVM被广泛应用于模式识别、回归分析和密度估计等领域,并取得了较好的效果。在通信信号处理领域,文献[4]将SVM应用于信道均衡,文献[5]利用SVM解决CDMA系统中的多用户检测问题,文献[6]提出了一种复杂度较低的SVM多分类算法用于提升多源位置相移键控(M-ary Position Phase Shift Keying,MPPSK)系统的信号检测性能,但上述文献都未给出完整的基于SVM的信号解调算法框架,也未考虑同步误差及色噪声等因素对算法性能的影响。
本文将信号解调看成有限样本的学习问题,即根据接收数据中的训练样本学习估计采样数据与解调结果之间的依赖关系,依据此依赖关系对未知数据的解调结果做出尽可能准确的预测,给出了基于SVM的信号解调算法,并仿真分析了精确同步、存在定时误差、存在相位误差、高斯色噪声等不同条件下的算法性能,验证了SVM应用于信号解调的有效性。
2 算法模型
基于SVM的信号解调模型如图1所示,信道建模为滤波器h(t),r(t)为残留定时误差和载波频偏的信号,即
r(t)=s(t;φ,τ)+n(t)。
(1)
式中:n(t)为高斯白噪声;φ和τ分别为残留相位误差和时延误差。

图1 基于SVM的信号解调模型
利用接收数据构造如下训练样本集合(xn,yn),n=1,2,…,N,其中N为训练序列的长度,而
xn=[r(n)…r(n-M+1)]T,
(2)
yn=a(n-L)∈{±1},
(3)
即xn为利用接收数据构造的M维输入数据,输出yn为发送数据s(t)中的训练序列符号的L(L≤M)个延迟采样。需要指出的是,M和L的不同大小会改变输入xn和输出yn之间的依赖关系,从而影响解调性能。M和L的最佳取值由不同的信道条件和接收机的同步性能决定。
3 算法描述
基于SVM的信号解调算法将信号解调转化为一个分类问题,采用SVM作为分类器完成信号解调。依据发送数据为+1还是-1,将接收信号分为两类;利用接收信号中的训练序列构造SVM的输入训练样本,并训练得到最优超平面;通过得到的最优分类超平面对采样数据进行分类,完成未知数据的解调。这就是基于SVM的信号解调算法的原理。
考虑到信道衰落和定时误差等因素,接收数据可能是非线性不可分的。对于非线性情况,SVM采用非线性映射φ把数据从低维空间映射到一个高维特征空间,在高维特征空间中寻找分类超平面:
(wT·φ(x))+b=0。
(4)
式中:w为权值向量;b为偏移量;(·)表示内积运算。为了得到最优分类超平面,SVM采用了结构风险最小化准则,求解如下最优化问题:

(5)

(6)

(7)
求解式(7),得到SVM分类器的输出为

(8)


(9)
基于SVM的信号解调算法如下:
(1)以Ts为采样周期,对接收机端输出信号进行采样,按照式(2)和式(3)构造训练样本集D={(xn,yn),n=1,2,…,N},其中N为训练样本长度;
(2)利用样本集D训练SVM得到最优分类超平面,将训练样本分成两类,其中一类代表发送信号为+1,另一类代表发送信号为-1;
(3)根据最优分类超平面对采样信号进行分类,得到未知数据的解调结果。
4 性能仿真
本节以误码率为衡量指标,分析评估不同信道条件下的基于SVM的信号解调算法性能,并与传统的基于匹配滤波器的解调算法相比较。文献[4]给出的基于SVM的信道均衡算法的性能可以逼近贝叶斯算法,能较好地解决信道h(t)引入的码间干扰问题。本文主要考虑定时误差和相位误差对解调性能的影响。
仿真1:高斯白噪声信道下,设残留定时误差τ和相位误差φ都为0,考察基于SVM的信号解调算法和基于匹配滤波器的解调算法的性能。设定算法中的M=1,L=0。为了不失一般性,仿真数据采用BPSK调制,升余弦滤波器滚降系数设为0.2,接收数据每码元一采样,长度为1 200点,训练数据长度N为200点,用1 000点长度的测试数据验证解调性能,蒙特卡洛仿真次数为1 000。信噪比SNR=10×lg10(Eb/N0),两种算法的解调误码率(BitErrorRatio,BER)随信噪比的变化曲线如图2所示。

图2 无定时误差和相位误差时误码率曲线
仿真2:高斯白噪声信道下,设残留定时误差τ=0,相位误差φ分别设为0.5 rad和0.6 rad时,考察基于SVM的信号解调算法和基于匹配滤波器的解调算法的性能。接收数据点数、调制方式、采样率等和仿真1相同,两种算法的误码率性能如图3所示。
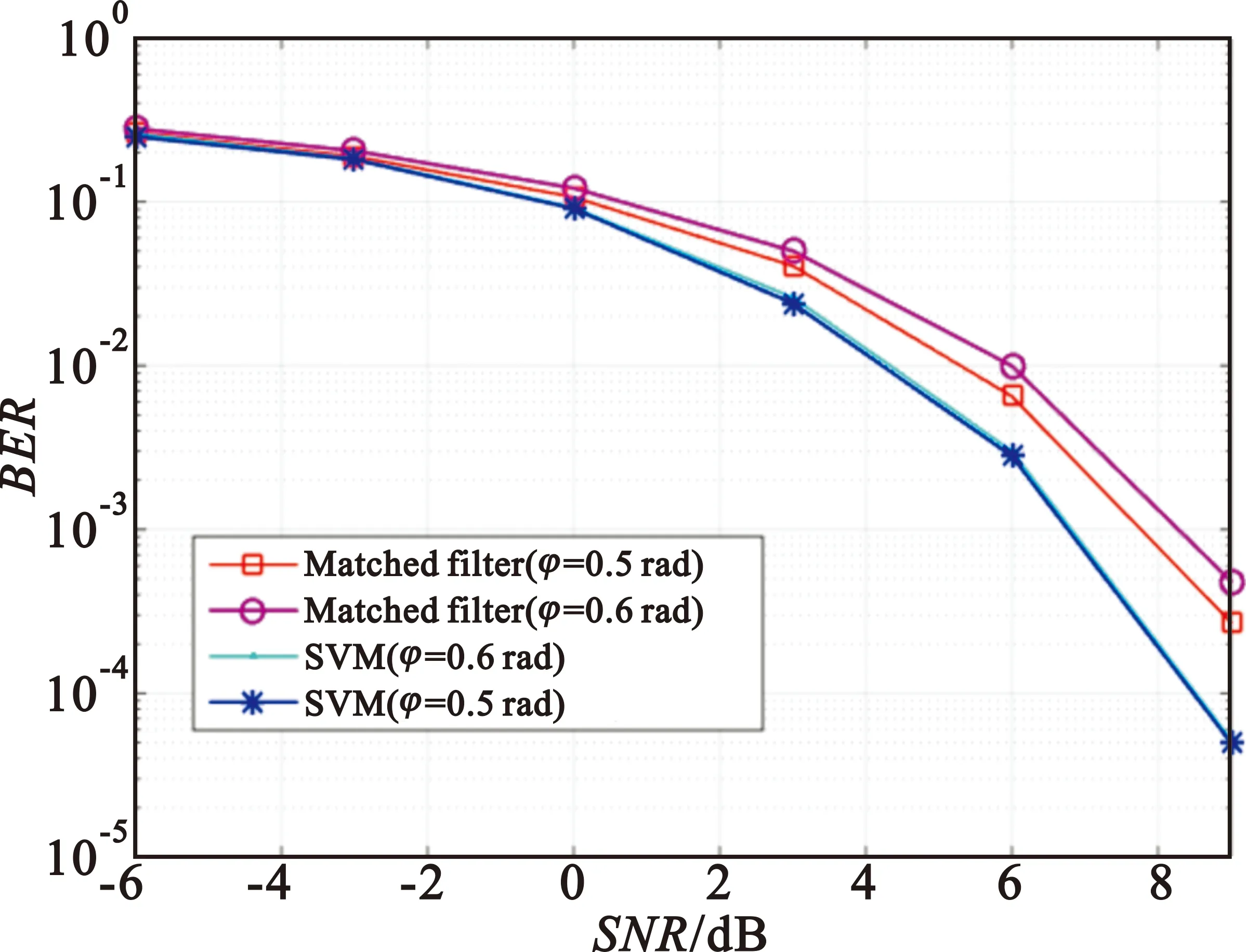
图3 残留相位误差时误码率曲线
仿真3:高斯白噪声信道下,残留相位误差φ=0,分别设定时误差τ=0.12Ts和τ=0.15Ts,其中Ts为采样周期。未知的定时误差在改变当前采样点能量的同时,还引入一定程度的码间干扰。设定算法中的输入样本维数M=3,判决延时L=1。接收数据点数、调制方式、采样率等和仿真1相同,基于SVM的信号解调算法和基于匹配滤波器的解调算法的性能比较如图4所示。
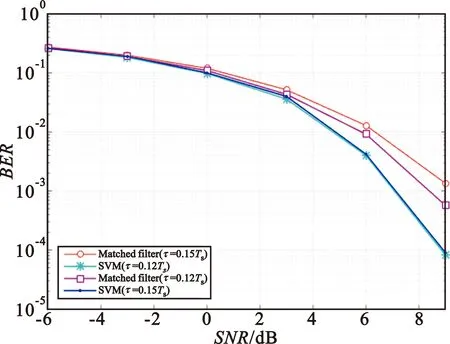
图4 残留定时误差时误码率曲线
仿真4:考察高斯色噪声信道下的解调算法性能。参照文献[7]的方法,利用滤波器{1 1.2 0.36}生成色噪声。接收数据点数、调制方式、采样率等和仿真1相同,两种算法的解调误码率BER随混合信噪比的变化曲线如图5所示。

图5 高斯色噪声信道下误码率曲线
分析以上仿真,可以得出以下有意义的结论:
(1)高斯白噪声信道下,无残留定时误差和相位误差时,基于SVM的信号解调算法能较好地逼近基于匹配滤波器的解调算法;
(2)基于匹配滤波器的解调算法性能受到了接收数据中的未知相位和定时误差的影响,性能随着相位差和定时误差的增大而恶化;
(3)由于残留相位不会改变整个接收数据样点之间的大小关系,因此不会影响基于SVM的信号解调算法的性能;
(4)基于SVM的信号解调算法能较好地克服定时误差引入的相位误差和码间干扰;
(5)高斯色噪声信道下,基于SVM的信号解调算法的性能要明显优于匹配滤波器算法。
5 结束语
围绕同步误差引起信号解调性能下降的问题,本文提出了一种基于SVM的信号解调算法,通过提高判决端的处理能力来改善系统的接收性能。在精确同步、存在定时误差、存在相位误差、高斯色噪声等不同条件下,本文进行了基于SVM的信号解调算法的性能仿真,结果表明:在精确同步条件下,SVM解调算法性能和匹配滤波器算法性能相当;在存在同步误差及色噪声条件下,SVM解调算法性能要优于匹配滤波器算法。SVM良好的泛化性能可较好地克服相位误差、定时误差及色噪声等因素对信号解调性能的影响。训练序列的构造中,M和L的取值对算法性能的影响较大,如何选取其最佳值是下一步的主要研究方向。
[1]梁津,潘龙禹,丁良辉,等.数字化短波调制解调器设计[J].电讯技术,2015,55(11):1283-1289.
LIANG Jin,PAN Longyu,DING Lianghui,et al.Design of a digital HF modem[J].Telecommunication Engineering. 2015,55(11):1283-1289.(in Chinese)
[2]WANG Y,DONG X D.Comparison of frequency offset and timing offset effects on the performance of SC-FDE and OFDM over UWB channels[J].IEEE Transactions on Vehicular Technology,2009,58(1):242-250.
[3]VAPNIK V N.Statistical learning theory[M].New York:Wiley-Interscience,1998.
[4]SANTAMARIA I,VIELVA L. Blind equalization of constant modulus signals using support vector machines[J].IEEE Transactions on Signal Processing,2004,52(6):1773-1782.
[5]王子磊,奚宏生.一种快速的在线SVM多用户检测算法[J].电子与信息学报,2006,28(8):1386-1390.WANG Zilei,XI Hongsheng.A fast online SVM algorithm for multi-user detection[J].Journal of Electronics and Information Technology,2006,28(8):1386-1390.(in Chinese)
[6]徐红梅,吴乐男.LDPC码在基于类二分法SVM的MPSK信号检测中的应用[J].东南大学学报,2014,44(3):468-471.
XU Hongmei,WU Lenan.Application of LDPC code in signal detection of MPPSK based on similar-dichotomy SVM[J].Journal of Southeast University,2014,44(3):468-471.(in Chinese)
[7]刘双平,闻翔,王志刚.色噪声中低信噪比单音正弦信号的频率估计[J].系统工程与电子技术,2007,29(6):866-869.
LIU Shuangping,WEN Xiang,WANG Zhigang. Frequency estimation of single sinusoid in colored noise at low SNR[J].Systems Engineering and Electronics,2007,29(6):866-869.(in Chinese)

滕晓云(1979—),男,山东莒南人,2010年于信息工程大学获通信与信息系统专业博士学位,现为工程师,主要研究方向为通信信号处理;
TENG Xiaoyun was born in Junan,Shandong Province,in 1979. He received the Ph.D.degree from Information Engineering University in 2010. He is now an engineer. His research concerns communication signal processing.
Email:xuasan2005@163.com
徐俊(1978—),男,江苏海县人,2000年于合肥工业大学获电子工程专业学士学位,现为工程师,主要研究方向为通信信号处理;
XU Jun was born in Haixian,Jiangsu Province,in 1978. He received the B. S.degree from Hefei University of Technology in 2000. He is now an engineer. His research concerns communication signal processing.
陈德明(1967—),男,江苏张家港人,高级工程师,主要研究方向为航天测控。
CHEN Deming was born in Zhangjiagang,Jiangsu Province,in 1967. He is now a senior engineer. His research concerns aerospace TT&C.
The National Natural Science Foundation of China(No.61403421)
A Signal Demodulation Algorithm Based on SVM
TENG Xiaoyun,XU Jun,CHEN Deming
(China Satellite Maritime Tracking and Control Department,Jiangyin 214431,China)
The estimation error of synchronization parameters will worsen the demodulation performance,when the training data is limited and the signal-to-noise ratio(SNR) is relatively low.For this problem,by treating demodulation as a learning problem using limited data which can be solved efficiently by support vector machine(SVM),a signal demodulation algorithm based on SVM is presented,which can improve the receiving performance through reforming the classification ability. The simulations are carried out with Matlab to compare the receiving performance in different circumstances such as precise synchronization,synchronization error,white Gaussian noise,colored Gaussian noise. The results show that the proposed algorithm can efficiently overcome the influence of synchronization error and colored noise on demodulation performance.
signal demodulation;support vector machine;phase error;timing error
10.3969/j.issn.1001-893x.2016.10.008
2016-01-04;
2016-05-25Received date:2016-01-04;Revised date:2016-05-25
国家自然科学基金资助项目(61403421)
TN911.7
A
1001-893X(2016)10-1108-04
引用格式:滕晓云,徐俊,陈德明.基于SVM的信号解调算法[J].电讯技术,2016,56(10):1108-1111.[TENG Xiaoyun,XU Jun,CHEN Deming.A signal demodulation algorithm based on SVM[J].Telecommunication Engineering,2016,56(10):1108-1111.]
**通信作者:xuasan2005@163.comCorresponding author:xuasan2005@163.com

