压缩感知宽带接收机设计及无杂散动态范围分析*
王桂良,陆路希
(盲信号处理重点实验室,成都 610041)
压缩感知宽带接收机设计及无杂散动态范围分析*
王桂良,陆路希**
(盲信号处理重点实验室,成都 610041)
为了分析压缩感知宽带接收机的性能损失,明确其适用范围,设计了一种基于调制宽带转换器(MWC)结构的压缩感知宽带接收机,并针对该接收机的无杂散动态范围进行仿真分析和实验测量。仿真分析和实测结果表明,字典基之间非正交性将会导致接收机无杂散动态范围的严重损失,在1/2压缩采样率的条件下,接收机无杂散动态范围仅能达到7 dB左右,这将严重限制压缩感知宽带接收机在高动态范围要求环境下的应用。
宽带接收机;压缩感知;字典基;无杂散动态范围分析
1 引 言
压缩感知的研究主要集中在稀疏表示方法、压缩观测矩阵设计和重构算法三方面,近年来均已取得了大量理论成果[1]。本文在这些成果的基础上,研究该理论的工程转化问题,通过理论仿真和实际系统测试,界定其在宽带信号采集中的适用范围。
压缩感知的工程化应用最早在光学领域,典型如单像素相机[2]、超谱成像仪[3]、微阵列传感器[4]。在电信号采集方面,莱斯大学Kirolos最早提出了Analogy-to-Information Converter(AIC)结构[5]。Mishali等人将AIC结构推广为多通道的形式,提出了调制宽带转换器(Modulated Wideband Converter,MWC)结构,并设计了Xampling接收机[6-7]。现有关于MWC类接收机的讨论多集中于准确地获取电路字典基[8],提高观测矩阵的性能[9],实验测试也多是在无噪声的理想环境下进行[6-7],对接收机在实际应用中的性能分析较少。Davenport等人针对高斯白噪声环境下的模拟信号采样进行了研究,他们发现压缩率每降低1/2,信噪比会因带内噪声放大损失3 dB[8],该结论对电信号压缩采样系统的性能分析具有重要指导意义,后续的实际测试也验证了这一结论[10]。
上述研究均建立在信号支集准确判定、信号有效重建的前提下,但在实际系统中,由于字典基向量的维数小于N,却仍要表示N维空间,无法保证两两正交,不正交的字典基间会产生混叠,这将在信号重构中引入重构误差,造成接收机性能的进一步恶化。非正交字典基之间混叠造成的性能损失,类似于传统接收机中的无杂散动态范围,直接关系到能够接收信号的动态范围,分析该指标有助于明确压缩感知宽带接收机的适用范围,但目前对该指标的研究相对较少。
针对上述问题,本文在MWC结构的压缩感知宽带接收机基础上,通过理论分析和仿真验证得出MWC结构的压缩感知宽带接收机在1/2压缩率条件下无杂散动态范围仅有7 dB左右的结论,并利用设计的接收机实测验证了这一结论。
2 系统设计
2.1理论模型
压缩感知的公式表示为
y=Φx=ΦΨα。
(1)
式中:向量x为待采集的信号;y为压缩观测向量;Φ为观测矩阵;通常压缩观测向量y的维度M远小于原始信号x的维度N,也即y是x在观测矩阵Φ上的投影压缩版本。上述压缩感知未考虑噪声影响,实际应用中噪声不可避免。Davenport等人将噪声因素加入到上述模型中来,建立了压缩感知的噪声模型:
y=Φ(x+n)+e
(2)
式中:n为输入噪声;e为测量噪声。他们从理论上证明输入噪声为白噪声情况下,每降低1/2的压缩率,信噪比至少损失3 dB[8]。
关于变换域Ψ的选择目前有多种方案,本文选取傅里叶变换矩阵为变换域矩阵。观测矩阵的设计一般在电路结构明确以后就是确定的,但由于实际器件实现过程中与理想值存在偏差,因此观测矩阵一般通过测量的方法获得。实测中我们发现,每次开机接收机观测矩阵均会发生细微变化,从而导致压缩字典基向量随之改变,影响信号重构性能。为了准确地获得这些会发生变化的字典基向量,本文的接收机增加了字典基自测功能。关于字典基自测技术其他相关论文已有阐述,这里不再赘述,仅简要介绍本文压缩感知宽带接收机的基本框架结构,并给出一个字典基自测及补偿的测试结果。
2.2基于MWC结构的压缩感知接收机设计
目前典型的压缩感知采样结构有AIC结构和MWC结构,本文采用相对更为实用的MWC结构,其基本结构框图如图1所示。

图1 MWC结构框图
图中Q个采样通道,每个通道对应一个伪随机序列,伪随机序列为N个码片的周期重复,其时钟周期等于实际的Nyquist采样率。第i个通道采样结果为

(3)
将采样结果离散化:

(4)
进一步将上述采样过程写成矩阵形式:
(5)
式中:Φi,K×N为第i个通道的观测向量,向量中元素取值为

(6)
这里{hi(0),hi(1),…,hi(L)}为模拟滤波器的等效数字化表示,伪随机序列pi(τ)赋予了上述观测矩阵伪随机特性,符合压缩感知对观测矩阵的特性要求。
本文接收机便是基于上述MWC结构,采用双通道结构。系统设计采样率40 Msample/s,工作在单通道模式下,AD速率40 Msample/s;双通道模式下AD采样率20 Msample/s,压缩率1/2的情况下,对应80 Msample/s的Nyquist采样率,覆盖频段0~40 MHz。接收机结构如图2所示。

图2 接收机系统组成
图2中两个AD通道即为上文中的MWC采样前端,DA通道用于输出字典基自测信号,伪随机序列采用TTL双电平表示,序列周期6.4 μs,每个周期包含512个符号,符号速率80 Msample/s。由于变换域采用傅里叶矩阵形式,因此自测信号为512组频率初始相位不同的正弦信号,且自测信号的周期与伪随机序列周期相同。为保证输出自测信号不发生失真,DA通道的回放速率取240 Msample/s。
图3给出了本文接收机的工作流程,开始时首先将DA通道连接到信号输入端,DA通道产生字典基自测信号,由采样通道采集并保存。字典基自测完毕后,将实际信号接入AD通道的输入端,开始压缩采样过程。由于上位机处理能力有限,这里先将采集数据进行存盘,再进行后续离线的信号重构、分析处理等操作。在已知信号载频、调制速率的情况下,信号重构的支集已知,重构算法的复杂度大大降低,上位机能够支持实时重构解调。

图3 接收机工作流程
2.3压缩感知宽带接收机杂散性能分析
如前所述,本文接收机变换域采用傅里叶矩阵。由于实际器件只能实现实数形式的傅里叶矩阵,因此我们的字典基测试采用一组实数域频率和相位不同的正弦信号,其形式为

(7)
伪随机周期序列共有512个符号,字典基的自测信号个数与伪随机序列的符号数相同,因此自测信号为512组频率相位变化的正弦波。期望达到80 Msample/s的Nyquist速率,式(7)中每个正弦波自测信号的实际频率为80f/512 MHz,其中f=0,1,2,…,255。由于DA速率为240 Msample/s,因此6.4 μs的伪随机序列周期内,正弦波自测信号共有1 536个数据样点,即n=1,2,…,1 536。式中k的取值为1或0,用于控制自测信号相位。为获得较为准确的字典基测量结果,可以多次发送自测信号,将测量结果取平均作为最终的测量值。频率相同、相位相差π/2的两个字典基测量结果合成一个复数形式的傅里叶向量的字典基,作为后续信号重构的基础。
公式(2)中,一般稀疏表示基向量ψ(i)是两两正交的,是N维空间的完备正交基集合,但字典基向量θ(i)的维数小于ψ(i),却仍然要表示N维空间,所以无法保证两两正交,不正交的字典基间会产生混叠。这使得除字典基本身频率之外的其他频率上将会出现能量泄露。基于MWC结构,我们仿真分析了所设计的接收机在1/2压缩采样率条件下的字典基最大杂散功率情况,如图4所示。从图中可以看出字典基的频率响应同最大杂散之间的功率差仅有7.5 dB左右。

图4 字典基的频率响应和最大杂散的仿真结果
下面以重构算法中常用的正交追踪匹配(Orthogonal Matching Pursuit,OMP)算法[12]为例来说明上述字典基之间的非正交性对信号重构造成的影响。应用OMP法进行稀疏信号估计基本步骤如下:初始化残差r0=y,设置α中非零元素下标集合Λ0=∅,迭代次数t=1。
(1)求解如下优化问题来确定本次迭代得到的非零元素下标λt:

(8)
式中:θ(i)表示Θ的第i列。
(2)向下标集合以及矩阵非零元素集合中增加一个元素,即Λt=Λt-1∪{λt},Θt=[Θt-1,θ(λt)]。
(3)求解最小均方误差优化问题αt=min‖y-Θtα‖2得到信号新的估计值。
(4)计算估计残差yt=Θtαt,rt=y-yt。t=t+1,若t 求解αt=min‖y-Θtα‖2通常采用的是最小二乘法,即 (9) 这里假设y=biθ(i)+bjθ(j),i≠j,且 lg(b1)-lg(b2)≥7.5 。 (10) 则 (11) 在θ(i)、θ(j)正交的情况下,利用上式可以准确求出bi、bj,从而正确重构原始信号,但在θ(i)、θ(j)非正交的情况下, (12) 从前面的仿真结果可知,在最恶劣的情况下, (13) 由式(10),θ(i)分量的能量高于θ(j)分量的能量,此时 (14) 对于θ(j)分量,其估计误差跟实际信号能量接近,从而导致bj无法准确估计。即当强信号和弱信号的功率差超过7.5 dB时,弱信号无法准确恢复。 在实验室环境下测试接收机无杂散动态范围性能,利用信号源E4438C产生测试信号,利用压缩感知宽带接收机采集测试信号,利用处理软件对压缩采样数据进行离线重构,重构为等效80 Msample/s采样率的波形文件,再进行后续分析。 首先测试压缩感知接收机的单频响应情况,结果如图5所示。为说明本接收机频率覆盖能力,测试信号选取频率为26.56 MHz的单频信号。图5(a)显示了伪随机序列为全1(即不做伪随机观测)、40 Msample/s采样的字典基响应,即40 Msample/s正常采样的频谱响应。由于此时Nyquist无混叠带宽为20 MHz,因此13.44 MHz处出现了该单载波的镜频成分,功率和原信号基本相同。图5(b)为伪随机序列正常工作的40 Msample/s压缩采样的字典基响应,可见13.44 MHz镜频处的响应已被抑制,这证明了本文压缩感知宽带接收机的有效性,但由于压缩字典基非正交,相互间产生干扰,噪底被整体抬升。从图中可以看出,同正常采样的信号相比,压缩采样信号的无杂散动态范围大大降低了。 图5 正常采样和压缩采样的单频信号响应 接下来测试接收机全部字典基向量的自相关和互相关特性,每个字典基向量的自相关可视为该频点的频率响应,不同字典基向量的互相关可视为相互间的杂散,图6给出了所有字典基向量的频率响应和最大杂散的比较,类似于传统接收机的无杂散动态范围测试。同图4相比,仿真结果没考虑传输损耗,在0~40 MHz内响应和杂散基本平坦,实际电路存在随频率变化的传输损耗,在30 MHz范围内的最大损耗为3 dB。实测在0~40 MHz范围整体频率响应和最大杂散相差约7 dB,跟仿真结果接近。这表明本接收机40 Msample/s采样可以无混叠地覆盖40 MHz带宽,突破了传统采样理论的无混叠带宽不超过采样率的一半的限制。然而,对于一般接收机而言7 dB的无杂散动态范围是极差的,这是由于基向量长度被压缩导致非正交引起的,只要基向量的长度小于其所表示的空间维数就会存在这种损失,是压缩感知不可避免的。 图6 字典基的频率响应和最大杂散的实测结果 本文根据压缩感知原理研制实现了一套MWC结构的接收机,给出了接收机的具体设计方案,实验验证了该接收机以40 Msample/s采样率无混叠覆盖0~40 MHz频率范围的能力。本文通过仿真实验和接收机实测结果表明压缩感知宽带接收机将面临由于字典基非正交带来的无杂散动态范围损失,基于MWC结构的压缩感知宽带接收机在1/2压缩率条件下无杂散动态范围仅能达到7 dB左右,当强弱信号的功率差超过7 dB时,弱信号将无法准确恢复。动态范围的损失是压缩感知宽带接收机除了信噪比之外的另外一项重要性能的损失,将会限制压缩感知宽带接收机在大动态范围需求场合的应用,这也是今后的主要研究内容。 [2]LASKA J,KIROLOS S,DUARTE M,et al.Theory and implementation of an analog-to-information converter using random demodulation[C]//Proceedings of 2007 IEEE International Symposium on Circuits System(ISCAS). Louisiana,New Orleans:IEEE,2007:1959-1962. [3]MISHALI M,ELDAR Y C,ELRON A J. Xampling:signal acquisition and processing in union of subspaces[J].IEEE Transactions on Signal Processing,2011,59(10):4719-4734. [4]MICHAELI T,ELDAR Y C. Xampling at the rate of innovation[J].IEEE Transactions on Signal Processing,2012,60(3):1121-1133. [5]TREICHLER J,DAVENPORT M,BARANIUK R.Application of compressive sensing to the design of wideband signal acquisition receivers[C]//Proceedings of the 6th U.S./Australia Joint Workshop on Defense Applications of Signal Processing(DASP). Lihue,Hawaii:IEEE,2009:1-10. [6]DAVENPORT M,LASKA J,TREICHLER J,et al.The pros and cons of compressive sensing for wideband signal acquisition:noise folding versus dynamic range[J].IEEE Transactions on Signal Processing,2012,60(9):4628-4642. [7]MALEH R,FUDGE G L,BOYLE F A,et al.Analog-to-information and the Nyquist folding receiver[J].IEEE Journal on Emerging and Selected Topics in Circuits and System,2012,2(3):564-578. [8]CHEN Y,MISHALI M,ELDAR Y C,et al.Modulated wideband converter with non-ideal lowpass filters[C]//Proceedings of 2010 IEEE International Conference on Acoustics Speech and Signal Processing(ICASSP).Dallas,Texas:IEEE,2010:3630-3633. [9]YANG X,TAO X,GUO Y J,et al.Subsampled circulant matrix based analogue compressed sensing[J].Electronics Letters,2012,48(13):767-768. [10]程艳合,杨文革,韩丙寅.宽带直扩信号的随机解调压缩采样方法[J].电讯技术,2015,55(5):472-478. CHENG Yanhe,YANG Wenge,HAN Bingyin.Compressive sampling of broadband DS signal based of random demodulation[J].Telecommunication Engineering,2015,55(5):472-478.(in Chinese) [11]TROPP J A,GILBERT A C. Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory,2007,53(12):4655-4666. 王桂良(1987—),男,山东潍坊人,博士研究生,主要研究方向为稀疏信号处理和辐射源指纹识别; WANG Guiliang was born in Weifang,Shandong Province,in 1987. He is currently working toward the Ph.D.degree. His research concerns spare signal processing and specific emitter identification. Email:wangguiliang05@gmail.com 陆路希(1982—),男,上海人,博士,工程师,主要研究方向为稀疏信号处理和通信信号处理。 LU Luxi was born in Shanghai,in 1982. He is now a now an engineer with the Ph.D.degree. His research concerns spare signal processing and communication signal processing. Email:luluxi@pku.edu.cn China Postdoctoral Science Foundation(2013M532238) Design and Spurious-free Dynamic Range Analysis of a Compressed Sensing Wideband Receiver WANG Guiliang,LU Luxi (Science and Technology on Blind Signals Processing Laboratory,Chengdu 610041,China) In order to analyze the performance loss and application of compressed sensing wideband receiver,the design detail of a compressed sensing receiver is provided based on modulated wideband converter(MWC) structure. Simulations and experiments are performed to measure the spurious-free dynamic range(SFDR) of the receiver. The result shows the large SFDR loss of the receiver caused by the non-orthogonality of dictionary atoms.When compressed at the ratio of 1/2,the SFDR of the compressed sensing wideband receiver is about 7 dB,which will severely limit its application in high dynamic range requirements. wideband receiver;compressed sensing;dictionary atom;spurious-free dynamic range analysis 10.3969/j.issn.1001-893x.2016.10.007 2015-12-31; 2016-07-08Received date:2015-12-31;Revised date:2016-07-08 中国博士后科学基金资助项目(2013M532238) TN850 A 1001-893X(2016)10-1103-05 引用格式:王桂良,陆路希.压缩感知宽带接收机设计及无杂散动态范围分析[J].电讯技术,2016,56(10):1103-1107.[WANG Guiliang,LU Luxi.Design and spurious-free dynamic range analysis of a compressed sensing wideband receiver[J].Telecommunication Engineering,2016,56(10):1103-1107.] **通信作者:luluxi@pku.edu.cnCorresponding author:luluxi@pku.edu.cn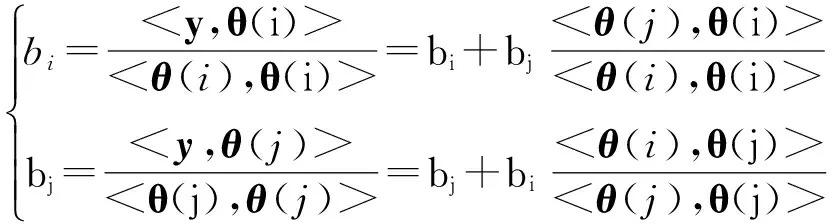


3 测试分析


4 结束语


