基于遗传算法的多阶段动态批量生产问题研究

东 博，朱小林

(上海海事大学物流研究中心， 上海201306)



基于遗传算法的多阶段动态批量生产问题研究

东 博，朱小林

(上海海事大学物流研究中心， 上海201306)

在生产系统的供应链中，有已有制造线和再制造线两个阶段，合理安排两个阶段的生产计划是实现成本最小化的关键。考虑库存费用、制造全新产品数量和再制造产品数量的因素下，建立面向再制造线和已有制造线两阶段的动态批量生产成本优化模型，针对这一模型设计了自适应遗传算法并结合实际案例对问题求解，给出了合理的生产计划，实验表明:该遗传算法对解决多产品的动态批量问题有良好效果。

再制造；动态批量生产；自适应遗传算法

0 引 言

随着社会的发展，人们的环境意识越来越高，环境保护政策也颁布了许多。很多企业通过产品回收这一过程，来降低产品对环境造成的破坏；另外，考虑到经济性，越来越多的企业在参与产品回收过程中，对回收产品进行再制造，获得额外价值以及更高的利润。在整个供应链里，再制造就是一项回收活动，对回收的产品重新利用或者重新制造，可以得到与新产品相同性能的再制造产品，这些产品同样可以满足客户的需求，这样不但降低制造成本还获得比较丰厚的利润。

但是对于企业来讲，将现有的生产系统和再制造进行结合，最关键的是获得最大利润。

文献[1]中以前研究生产问题时，没有考虑过产品回收这一项，而现在很多研究人员开始考虑了产品回收这一项，并将此项和整个生产计划进行结合；

文献[2]中学者Schrady针对经典EOQ模型稍微进行了改进，在此模型中将产品回收考虑了进去，但是文献没有考虑到批量问题；

文献[3～5]对Schrady的模型进行了再次扩展，这次考虑了采购和回收批量问题；

文献[6]不再假设连续回收处理条件，研究产品回收只在一定期限内发生的经济批量问题；

文献[7]和文献[8]利用现有数学模型对多产品生产以及再制造经济生产问题进行了研究；

文献[9]在总结供应商选择准则方法等相关研究成果的基础上,以模糊理论为依托,从定量的角度分别研究了在包含模糊和随机信息、存在供应中断、折扣价格条件下的供应商选择及订单分配问题；

文献[8～12]针对再制造产品和新产品同时满足需求的生产批量问题，在条件有限时间内需求和退货量一定的情况下，建立了目标为成本最小的模型；

文献[13]针对在需求已知并且动态，且时间段有限的条件下安排生产，提出了多阶段的多目标函数，在求解过程中引进VND进行求解，并且在求解的过程中讨论了不同个数可变领域对结果优劣性的影响，并在最后与前学者所提出的Gurobi算法进行对比，验证了VND的有效性；

文献[14]中做了一项调查，关于美国再制造企业中，影响生产计划和控制活动的因素有7个，主要有回收物流时间和数量上的不确定性、回收物流和产品需求难以一致性、拆卸、物流修复不确定性、逆向物流、物料匹配要求以及产品加工时间不确定性；

文献[15]运用Wagner/Whitin算法证明了再制造生产计划模型存在零库存性质；

文献[16～18]通过利用前人的研究，推广和应用了Wagner/Whitin算法，解决现有制造和再制造的混合系统生产问题，并还解决基于动态规划的精确多项式优化问题。文献[6～17]将线性规划方法应用于确定型闭环供应链生产计划中。

然而，以往的多数文献要不只考虑现存制造线，要不只考虑了再制造线并提出相关模型和算法，只有少数文献中同时考虑到再制造和现存制造两个阶段，而本文既考虑了再制造线也考虑到现存制造线，合理安排这两个阶段，在库存费用、制造全新产品数量和再制造产品数量的因素下，建立动态批量生产成本优化模型，设计自适应遗传算法，结合实际案例求解，给出两个阶段的生产计划，这对以后研究这方面工作有一定的借鉴作用。

1 问题描述

在本文中，主要研究的是动态批量生产问题。在满足制造商生产计划条件下，制造商合理安排生产计划，从而减少制造成本和库存费用。其中，在制造商作生产计划时考虑了制造全新产品数量和再制造产品数量。

在不确定环境下优化制造商生产计划安排中，制造商需要做两种类型的决策：第一，是否建立制造线和再制造线被视为战略决策;第二，制造全新产品数量和再制造产品数量被视为战术决策。主要可描述为制造商根据每阶段市场需求生产产品，产品来源一部分来自制造线生产，另一部分来自再制造线生产。如果制造商制造的全新产品和再制造产品这两个来源缺乏合理协调会最终影响制造商生产计划以及不满足市场需求最终导致经济损失。如图1所示，制造商根据实际情况决定是否建立制造线和再制造线。

图1 动态批量生产流程图

2 模型建立

本文讨论的问题是在满足各时期需求时制造商成本最低。每一个阶段市场需求是已知的，由新产品和再制造产品满足，也知道所有周期的返回产品的数目，并假定是不固定的。回收的产品能够被再制造成新的产品，和新产品并无区别。

本节研究问题包括是否建立全新产品制造线和再制造产品制造线的多产品动态批量问题。所建立的模型是在以Sahling模型基础上建立的，其目的是确定制造和再制造在每个阶段生产的数量，为了尽可能减少建立制造线和再制造线以及所需要的设备花费的成本。

2.1 符号说明

k:生产数量，k=1,2,…,K;

t:生产阶段，t=1,2,…,T;

D(k,t):每个阶段t所需要的产品数量k;

R(k,t):每个阶段t可以被回收的产品数量k，并可以从新被再制造成新的产品;

hM(k):在每阶段每保存一单位的全新产品k的库存费用;

hR(k):在每阶段每保存一单位的再制造产品k的库存费用;

xM(k,t):在阶段t被生产的全新产品数量k；

xR(k,t):在阶段t被生产的再制造产品数量k；

kM(k):建立一条全新生产线的成本;

kR(k):建立一条再制造生产线的成本;

pM(k):生产一单位全新产成品的成本;

pR(k):生产一单位再制造产成品的成本;

yM(k,t):在每个阶段可以被存储的全新产品数量;

yR(k,t):在每个阶段可以被存储的再制造产品数量;

M:一个很大的数字;

k1:制造商每阶段可以储存的最大全新产品数量；

k2:制造商每阶段可以储存的最大再制造产品数量；

k3:制造商每阶段可以最多生产全新产品数量；

k4:制造商每阶段可以最多生产再制造产品数量；

2.2 模型建立

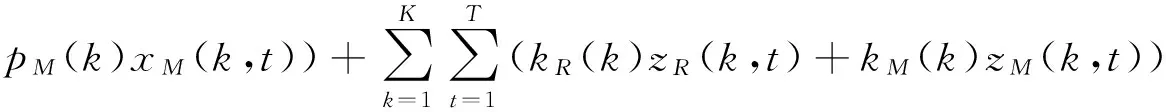
(1)

s.t.yR(k,t)=yR(k,t-1)+R(k,t)-xR(k,t), ∀t=1,2,…，T,∀k=1,2,…,K,

(2)

yM(k,t)=yM(k,t-1)+xR(k,t)+xM(k,t)-D(k,t), ∀t=1,2，…，T,∀k=1,2,…,K,

(3)

(4)

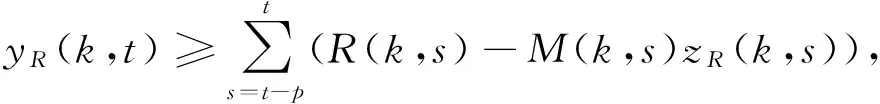
(5)

xR(k,t)+xM(k,t)≥D(k,t),

(6)

yM(k,t)≤k1,

(7)

yR(k,t)≤k2,

(8)

XM(k,t)≤k3,

(9)

XR(k,t)≤k4,

(10)

xR(k,t)≤MzR(k,t), ∀t=1,2,…,T,∀k=1,2,…,K,

(11)

xM(k,t)≤MzM(k,t), ∀t=1,2,…,T,∀k=1,2,…,K,

(12)

(13)

yR(k,0)=yM(k,0)=0, ∀k=1,2,…,K。

(14)

目标函数(1)表示制造商根据每阶段市场需求安排生产使其最后总成本最低；式(2)表示制造全新产品时每阶段库存等式关系；式(3)表示再制造产品每阶段库存等式关系；式(6)各阶段制造产品数量和再制造产品数量要满足市场各阶段需求；式(7)制造商每阶段可以储存全新产品的最大数量；式(8)制造商每阶段可以储存的最大再制造产品数量；式(9)制造商每阶段最多可以生产的全新产品数量；式(10) 制造商每阶段最多可以生产的再制造产品数量；式(11)和式(12)表示当设置生产全新产品线和再制造线时固定成本；式(13)和式(14)表示参数和决策变量非负。

3 算法求解

通过采用自适应遗传算法解决本文所研究的动态批量生产问题。

此算法采用全局搜索技术，起初生成多个生产方案，但这些方案不是最优方案，要根据所创建适应值的大小来进行排序，然后通过自适应遗传算法的一系列(选择、交叉、变异)过程，获得最优解。这种操作达到最大迭代代数为止。

3.1 初始种群生成

初始种群生成是以基因编码为基础，基因是染色体的单位，而一个染色体由若干基因组成。对于多阶段多产品动态生产问题的设计，一个染色体就表示一个生产方案。为了增加种群的多样性，本节随机生成初始化种群，检验初始化种群中每一个个体是否满足约束条件，去除不满足约束条件的个体，一直到初始种群个体达到N为止。

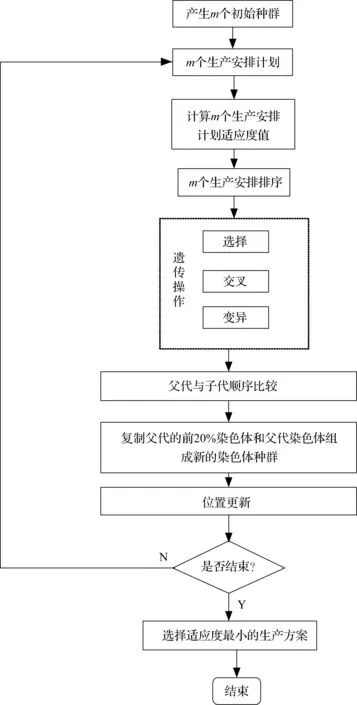
图2 基于遗传算法的生产方案优化求解策略

基于本文研究的问题是多阶段多产品动态生产问题，在本节的研究中产品的来源涉及到两方面，一方面是建立全新产品线生产全新产品，一方面是建立再制造线，生产再制造产品，根据市场的需求，每阶段产品的生产量(全新产品与再制造产品)要大于等于每阶段的需求量，鉴于问题的复杂性，本节设计2层整数编码方式。第一层代表全新产品线所制造的产品数量，第二层代表再制造线制造的产品数量。见图3所示。

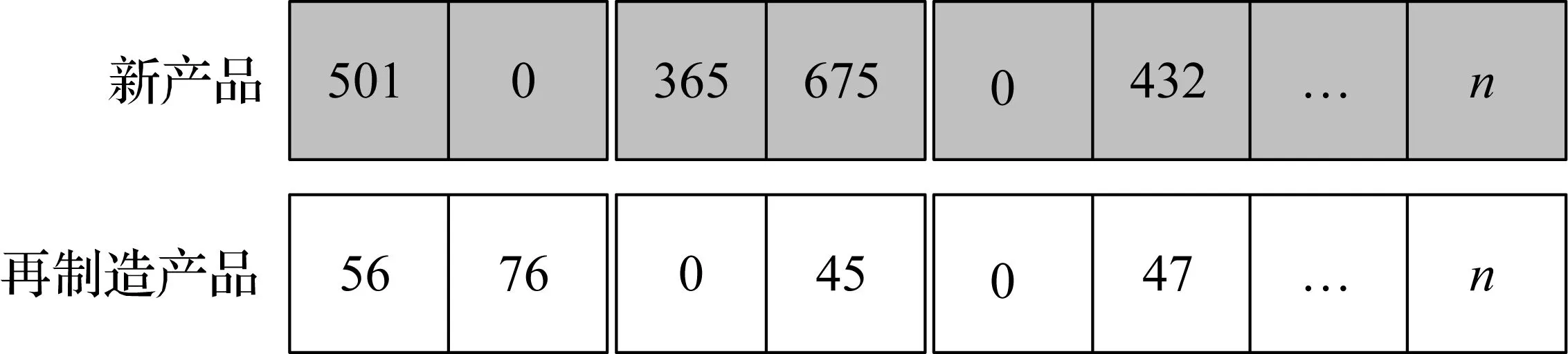
图3 编码

3.2 适应值

适应值是用来检测一个特定的染色体所表示的方案的优劣性，本文采用目标函数作为染色体的适应值。

3.3 遗传操作

①选择

从生成出来的种群中选取适应值高的染色体的行为叫选择，将适应度值高的前20%染色体复制到下一代和父代染色体组成新的染色体种群。通过该机制确保每代优秀个体不会在种群进化过程中丢失，确保优秀个体进入下一代，并且可以保证下一代种群中的最优个体不会比上一代差。

②交叉

交叉操作可以让优良的染色体从父代遗传到子代，所以交叉是此算法的一个关键操作，同时本节采用多层多点交叉法。具体方法如图4所示。

随机的选择两个父代p1，p2，交换切点位置上的基因值，若重新生成的染色体合法，则得到子代染色体c1、c2，若重新生成的染色体不满足约束条件则该子代染色体不合法，则对该子代染色体进行修复，应对策略为拒绝交叉。

图4 染色体交叉(黑白色)

③突变

突变就是由于各种原因引起遗传基因发生了改变。突变可以增加基因的多样性，使算法避免早熟。在第一层选中2个切点，在第二层选中2个切点，交换他们彼此的基因值。若编码合法，则生成子代染色体c1，见图5，若生成的子代染色体不满足约束条件则该染色体不合法，则对该子代染色体进行修复，应对策略为拒绝变异。

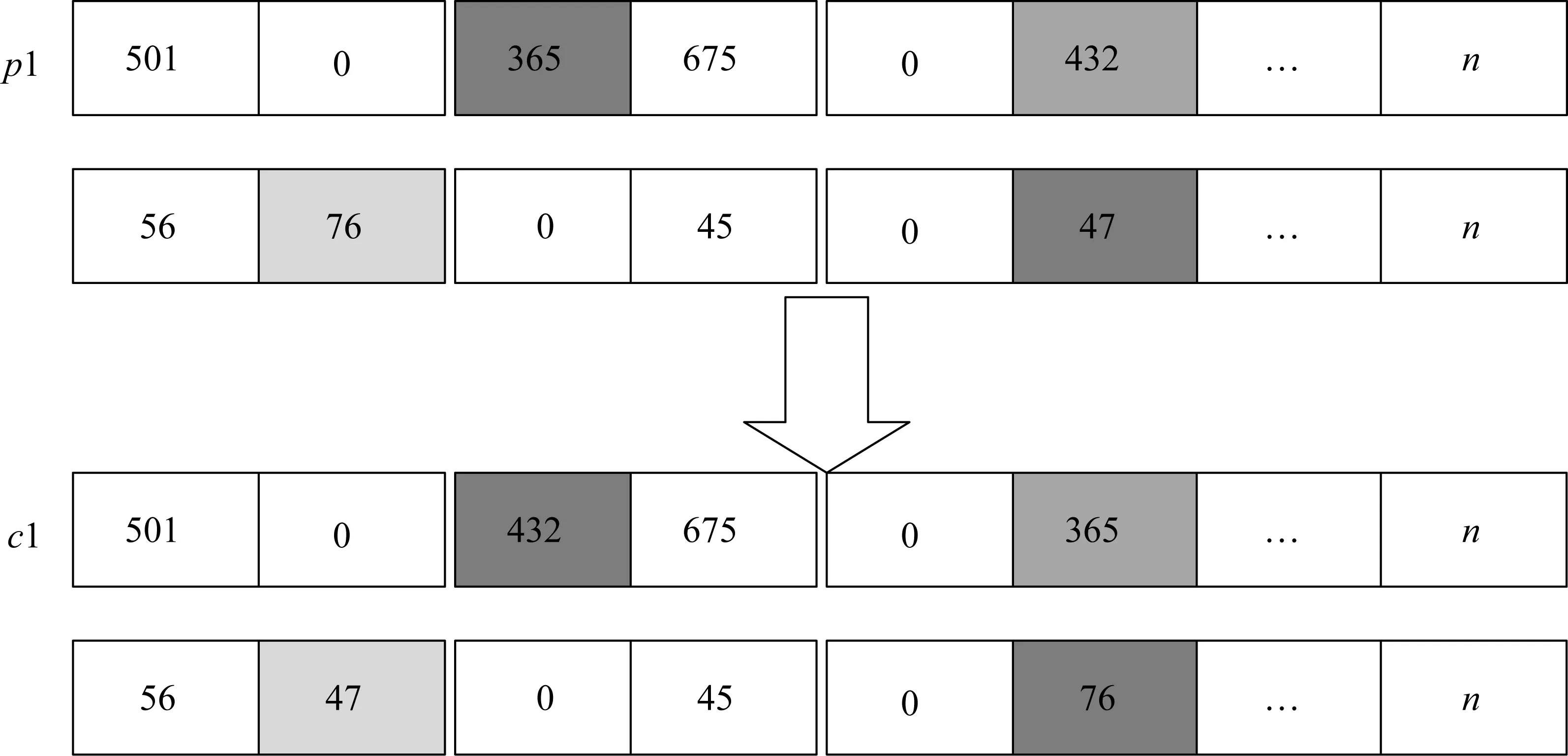
图5 变异

④交叉和突变概率

交叉概率pc和变异概率pm在遗传算法过程中起着重要的作用，相对于传统遗传算法，AGA首先判断种群代数，其次判断f与fave的大小，其特点为交叉和变异概率随着个体适应度、迭代代数的改变而改变。fmax为群体中最大的个体适应度值；f为要变异个体的适应度值，fave为每代群体的平均适应度值；x为当前迭代代数。N为迭代总代数。

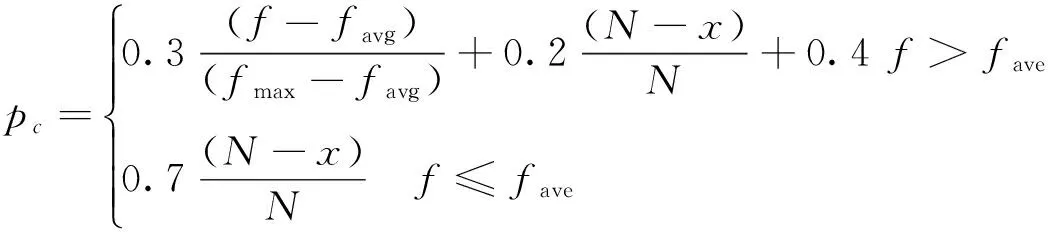
(15)

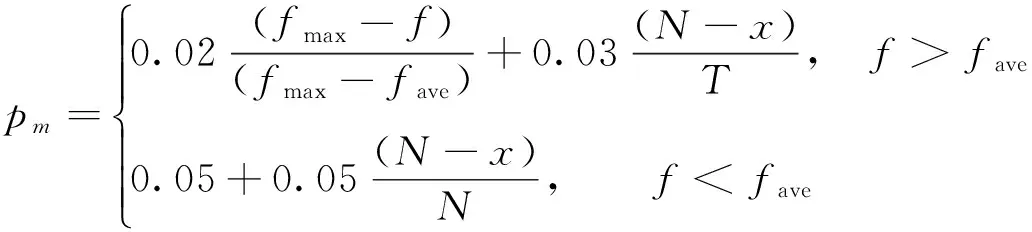
(16)

在交叉过程中，适应度高的染色体有更多机会产生新染色体，而当进化趋于稳定时，交叉的概率就会减少；即pc随着迭代代数增大而减少，pm也随着迭代代数增大而减少，此时适应值高的染色体会被保护起来；但是对于低于平均适应值的染色体要尽量通过突变来击破它，让它进行变化。

4 设计实例

某一制造企业每年生产10个月，每个月由于季节问题以及市场需求，所生产的产品数量是动态不确定的，制造企业为了满足市场需求，产品来源一部分是生产全新产品，一部分来自回收产品的再制造，每个月回收产品的数量见表1所示。储存一单位的hR(k)={0.2,0.5,0.8}，建立制造线成本kR(k)={200,500,2 000}，建立再制造成本kM(k)={200,500,2 000}。每个阶段的回收量服从均匀分布U(0,100)中生成，制造商每个阶段生产产品数量服从均匀分布U(0,1 000)。参数Popsize=100，最大迭代代数maxgen=500，pc、pm如上文所示。采用MATLAB语言编程实现算法开发。

表1 每个阶段需求量

5 结果分析

根据上述设置的遗传算法参数和求解步骤，利用自适应遗传算法对模型进行求解。制造商安排生产计划，分别针对不同储存单位hR(k)，建造制造线成本kR(k)，建造在制造线成本kM(K)有以下3种情况，见表2，通过Matlab计算分别可以获得它们的利润，并做出收敛图(图6)进行对比得到结论。

表2 制造商安排生产计划

图6 遗传算法收敛图

Fig.6 Genetic algorithm converges

6 结 语

在本文中，笔者已经解决了多产品的动态批量问题，产品回收和回收的逆向物流。在制造商、生产商作生产计划时，考虑回收产品对生产计划的影响，在建立约束条件时考虑库存费用以及生产控制合理安排生产全新产品数量和再制造产品数量，最后根据实际的企业生产控制计划提出了制造业成本最低的数学优化模型，假设了实例数据，采用遗传算法对该模型进行开发，并给出了合理的优化设计方案，实验表明，该遗传算法对解决多产品的动态批量问题有良好效果。

虽然本文对多产品的动态批量问题建立了相应的模型，并运用遗传算法求得最佳生产控制计划。但是在实际的多产品的动态批量问题中复杂程度远远大于理想状态，在实际生产过程中，还有许多因素需要考虑，例如回收产品价格的变化、原材料价格变化等。而这种扩展模型可以更切近实际问题，这将会成为今后研究的重点。

[1] SHORROCK B, ORLICKY J.Material requirements planning[J]. Encyclopedia of Operations Research & Management Science, 2009, 86(6):283-294.

[2] SCHRADY D A.A deterministic inventory model for repairable items[J]. Naval Research Logistics Quarterly, 1967,14(3):391-398.

[3] RCHTER K.An EOQ repair and waste disposal model[C]//Proceedings of the Eighth International Working Seminar on Production Economics. Austria: Innsbruck, 1994：83-91.

[4] RICHTER K.The EOQ repair and waste disposal model with variable setup numbers[J]. European Journal of Operational Research, 1996, 95(2):313-324.

[5] RICHTER K.Pure and mixed strategies for the EOQ repair and waste disposal problem[J]. Operations Research-Spektrum, 1997, 19(19):123-129.

[6] TEUNTER R H.Economic ordering quantities for recoverable item inventory systems[J]. Naval Research Logistics, 2001, 48(6):484-495.

[7] TANG O, RUUD T.Economic lot scheduling problem with returns[J]. Production & Operations Management, 2006, 15(4):488-497.

[8] 史玉雷，陆志强.基于供应商经济生产批量的供应链订单分配问题[J]. 上海交通大学学报, 2011, 45(12):1747-1752.

[9] 何东.L公司的多供给源选择与订货量分配研究[D]. 成都：电子科技大学, 2009.

[10]GUIDERJR V D R, JAYARAMAN V, SRIVASTAVA R.Production planning and control for remanufactureing: astate-of-art survey[J]. Robotics and Computer-Integrated Manufacturing, 1999,15(3):221-230.

[11]RICHTER K, SOMBRUTZKI M.Remanufacturing planning for the reverse Wagner/Within models[J]. European Journal of Operational Research, 2000,121(2):304-315.

[12]TEUNTER R H, BAYINDIR Z P, HEUVEL W V D.Dynamic lot sizing with product returns and remanufacturing[J]. International Journal of Production Research, 2006,44(20):4377-4400.

[13]GOLANY B, YANG J, YU G.Economic lot-sizing with remanufacturing options[J]. IIE Transactions,2001,33(11):995-1003.

[14]CLEGG A J, WILLIAMS D J, UZSOY R.Production planning for companies with remanufacturing capability[C]//Proceedings of the 1995 IEEE International Symposium on Electronics and the Environment. US: IEEE Service Center, 1995:186-191.

[15]JAYARAMAN V.Production planning for closed-loop supply chains with product recovery and reuse: An analytical approach[J]. International Journal of Production Research, 2006,44(5):981-998.

[16]WU Q H,CAO Y J,WEN J Y.Optimal reactive power dispatch using an adaptive genetic algorithm[J]. Electrical Power & Energy Systems,1998,20(8):563-569

(责任编辑 梁碧芬)

Research on multistage dynamic batch production problem based on genetic algorithm

DONG Bo, ZHU Xiao-lin

(Logistics Research Center, Shanghai Maritime University, Shanghai 201306, China)

In the supply chain of production system, there are two stages including already manufacturing line and re-manufacturing line. Reasonable arrangement for the production plans of the two-stage is a key to minimize costs. Considering the factors, such as the cost of inventory, the number of new product manufacturing and the remanufacturing quantity of product, a dynamic batch production cost optimization model for the two-stage manufacturing line is designed. The adaptive genetic algorithm associated with the model is also given, which gives the reasonable production plan in practical cases. The given experiments show that the genetic algorithm is good for solving the problem of dynamic multi-product batch production.

remanufacturing; dynamic mass production; adaptive genetic algorithm

2016-05-07；

2016-06-22

国家自然科学基金资助项目(11301334);上海市科委重点项目(12510501700)

朱小林(1975—)，男，湖南人，上海海事大学副教授;E-mail:zhuxl@shmtu.edu.cn。

东博，朱小林.基于遗传算法的多阶段动态批量生产问题研究[J].广西大学学报(自然科学版)，2016，41(5)：1594-1602.

10.13624/j.cnki.issn.1001-7445.2016.1594

F9; TP301.6

A

1001-7445(2016)05-1594-09