独轮车机器人驱动关节特性的分析及实验研究
庄 未,江 汉,朱赣闽,何淑通,张 帆
(桂林电子科技大学机电工程学院, 广西桂林541004)
独轮车机器人驱动关节特性的分析及实验研究
庄 未,江 汉,朱赣闽,何淑通,张 帆
(桂林电子科技大学机电工程学院, 广西桂林541004)
为了研究独轮车机器人驱动关节的特性,针对一台3驱动独轮车机器人样机,采用多种方法对其关节驱动电机的电流跟踪响应(正弦电流、指数衰减电流、阶跃电流)、速度跟踪响应(正弦速度、指数衰减速度)、力矩系数辨识以及车体俯仰平衡控制进行了实验和分析。研究结果表明,驱动关节对不同电流和速度曲线的跟踪响应在时域上存在一定滞后,但在幅值和频率上体现了良好的动态性能,且关节驱动电机的电流与关节的输出力矩具有较好的线性关系(τi=2.47I)。利用该关系并引入了基于部分反馈线性化设计的PD控制器即可达到一定的俯仰平衡控制效果。本研究明确独轮车机器人驱动关节特性对系统平衡控制的意义,可为独轮车机器人的其他平衡运动提供理论参考。
独轮车机器人;关节驱动特性;部分反馈线性化
独轮车机器人是一种轻便灵活、节能环保的新型道路行走机构,因其在快递物流、服务表演等行业具有潜在的应用而受到人们的关注[1-6]。
独轮车机器人独轮接地的特性决定其研究首先要解决平衡问题[1-6]。Schoonwinkel[7]采用线性LQR方法实现了其机器人的前后运动平衡,然而其控制器的鲁棒性有待提高。文献[8]中采用LQG的平衡策略使独轮车机器人具备了全方位稳定的能力,但这与机器人的实际工况仍有不同。文献[9]中提到的“村田婉童”平衡能力较强,但其相关核心内容至今尚未完全公开。Ho等[10]用Euler-Lagrange方法为其机器人建立了动力学模型,并使用了滑模控制和反馈线性化控制方法实现了自平衡控制。北京工业大学阮晓钢等[11-15]利用双闭环PID控制和滑模控制等控制策略对独轮车的平衡控制进行了研究,并取得了一定的进展。
本研究以一台具有3个驱动关节的独轮车机器人物理样机为研究对象,主要针对后续平衡运动控制进行驱动关节特性的理论分析和实验研究。首先,通过开展驱动关节的正弦电流跟踪、指数衰减电流跟踪、阶跃电流跟踪、正弦速度跟踪、指数衰减速度跟踪等曲线跟踪实验了解驱动关节的响应特性;其次,引入最小二乘法对驱动关节的电流—力矩关系进行辨识实验以进一步明确系统关节的驱动特性;最后,基于部分反馈线性化设计PD控制器进行前后俯仰平衡的控制实验,以验证实验的有效性,旨在明确其驱动关节特性对系统的平衡控制的重要意义。
1 样机系统简介
1.1 机械结构
本研究的独轮车机器人由车架、行走独轮、腰轮和摆轮组成,如图1所示。该机器人主要依靠行走独轮、腰轮和摆轮来调整车体的前后俯仰、航向和左右倾斜运动。它们的转动轴两两正交[图1(b)],以实现运动的部分解耦,从而降低系统建模和控制的复杂度。

(a) 机械结构
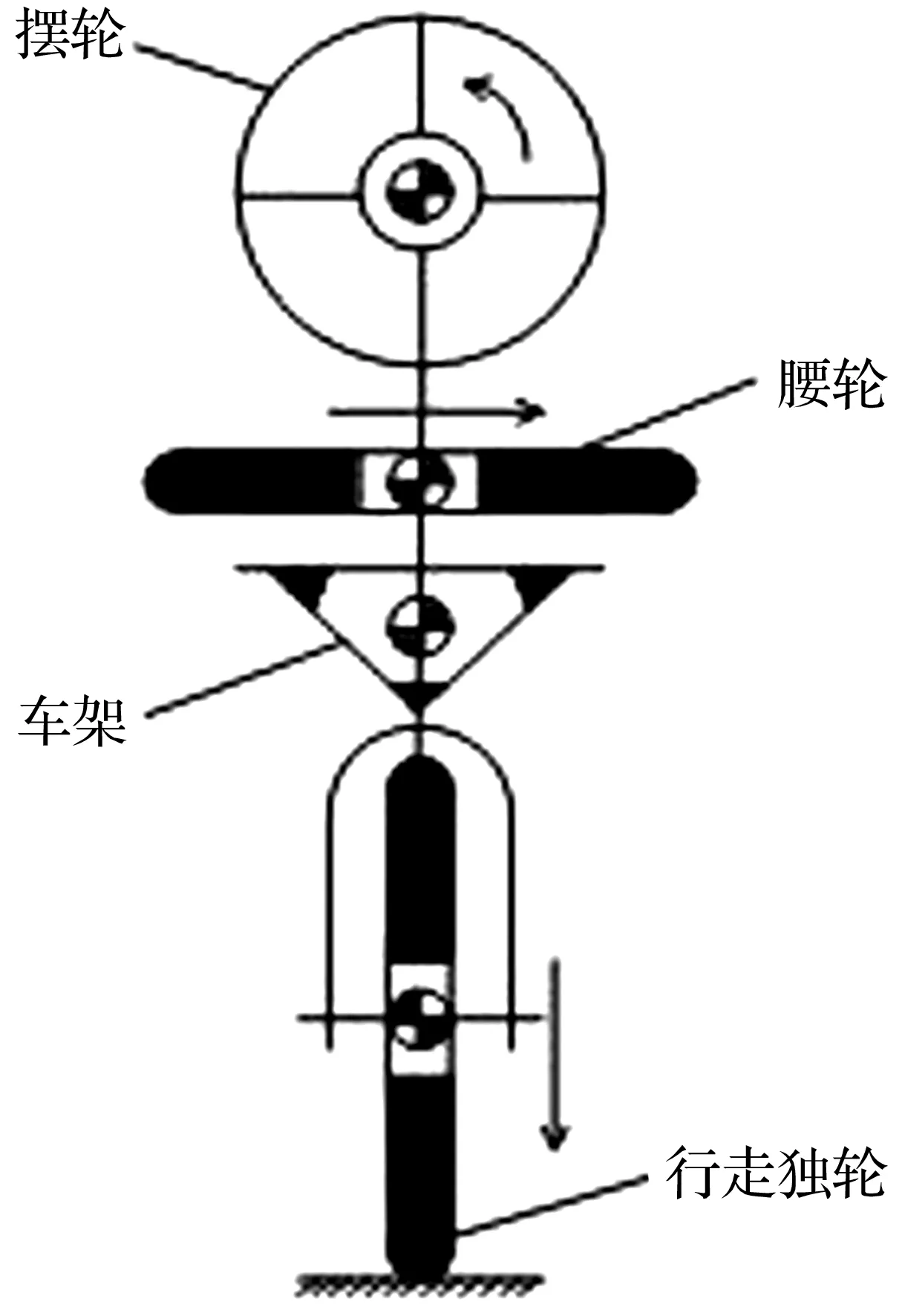
(b) 机构简图
1.2 测控系统
独轮车机器人测控系统分为本体部分和上位计算机两部分,其结构如图2所示。其中,数字信号处理器(DSP)TMS320F28335为控制算法计算核心;增量式光电编码器、惯性测量单元(IMU)和电流传感器用于系统的状态测量;ZigBee无线通信模块可以实现机器人本体和上位机的数据通讯;上位计算机主要负责系统状态监控以及轨迹规划、路径跟踪等上层决策的生成。这种移动式的单机器人系统是多机器人系统之间实现协调工作的基础[16]。
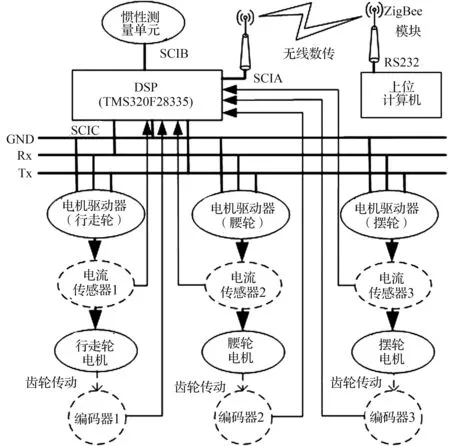
图2 独轮车机器人测控系统硬件框图
机器人上装有3个薄饼式直流电机,通过内啮合的减速齿轮为行走轮、腰轮和摆轮提供源动力。关节的直流电机驱动器结构如图3所示。
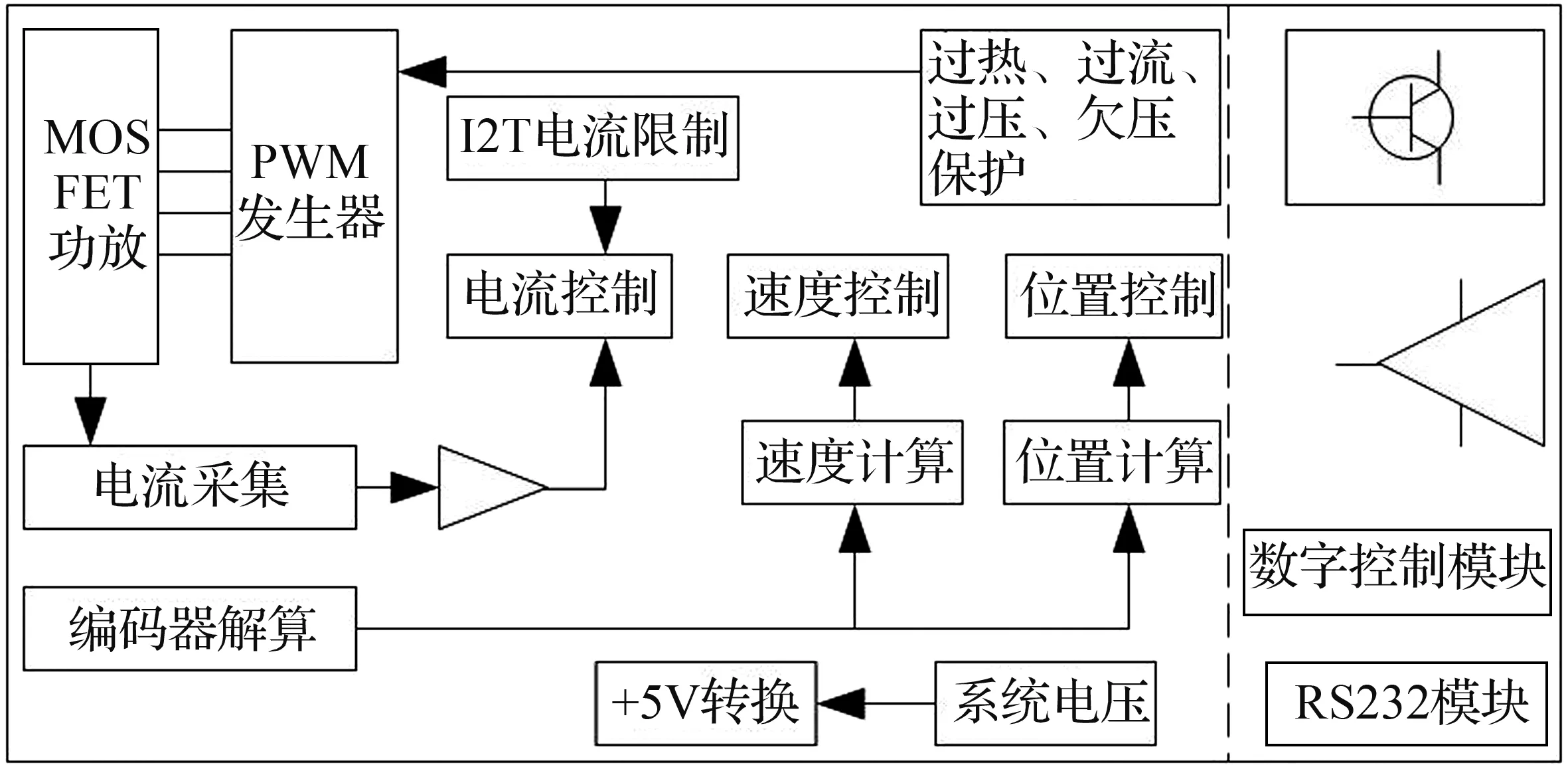
图3 关节电机驱动器的结构原理图
驱动器嵌入了高性能的16位DSP,可以提供位置模式、速度模式和电流模式的闭环驱动输出。另外,样机采用RS232总线的通讯模式,通过ID地址设置将3个驱动器组成网络。TMS320F28335发送ASCII码指令给驱动器,产生控制输出来驱动行走轮、腰轮和摆轮电机。
2 驱动关节电流和速度响应实验
独轮车机器人需要驱动关节施加力矩给行走独轮、摆轮和腰轮来控制车体的平衡和航向。由于样机的电机驱动器只能提供电流和速度闭环输出,因此,明确系统的电流和速度响应以及电流与力矩的关系对独轮车机器人平衡运动控制具有重要意义。
2.1 正弦电流跟踪响应实验
通过驱动器给关节驱动电机施加一个按正弦规律变化的电流,即:
I(t)=Asinωt,
(1)
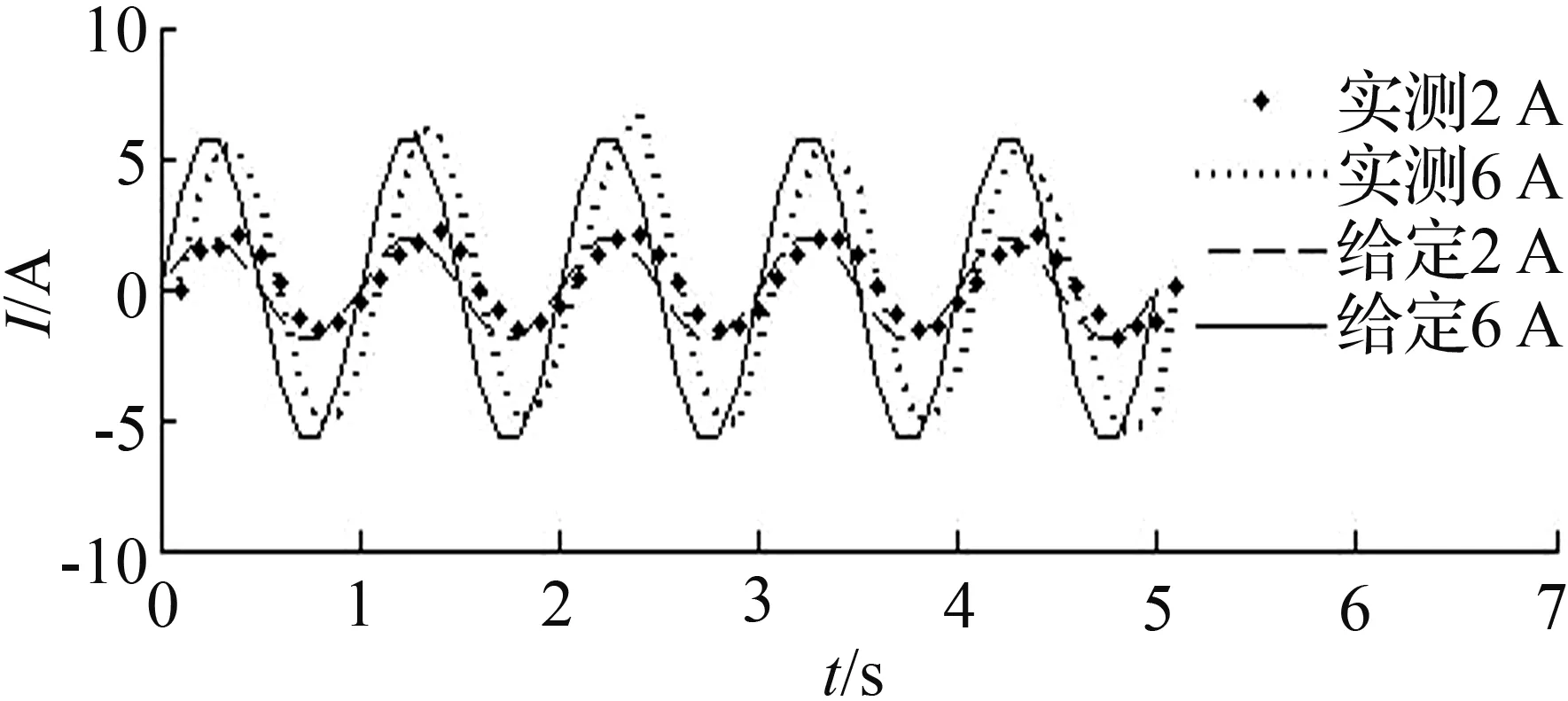
图4 正弦电流跟踪响应曲线Fig.4 Tracking curve of sine-wave current
式中,A为幅值,ω为角频率,且ω=2π/T,T表示周期。
实验结果如图4所示(由于篇幅关系,这里仅给出了周期为1 s的曲线跟踪响应图,其他周期的曲线跟踪响应有类似的结果)。由图4可知,响应电流与给定电流在幅值上存在误差,误差总体不超过0.5 A。另外,响应周期在时域上与给定值基本一致。此时系统伺服采样周期为0.1 s,响应大约有0.1 s的迟滞。
2.2 衰减电流跟踪响应实验
通过驱动器给关节驱动电机施加一个按指数衰减的电流(周期为1 s、幅值为6 A),即:
I(t)=Ae-σtcosωt,
(2)
式中,σ是一个与衰减速率有关的参数。
实验结果如图5所示。由图5可见,一方面,给定伺服采样周期为0.01 s,响应电流与给定电流的误差很小,具有良好的跟踪轨迹。另一方面,随着σ值的增大,响应电流具有明显的衰减趋势。这表明该测控系统具有较高的可靠性和灵敏度。

(a)σ=0.1
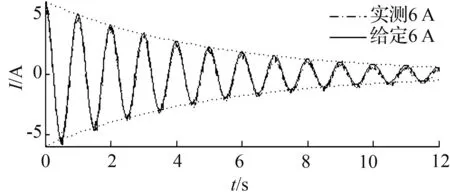
σ=0.2
图5 衰减电流跟踪响应曲线
Fig.5 Tracking curve of exponential decay current
2.3 阶跃电流跟踪响应实验
通过驱动器给关节驱动电机施加一个按恒值的响应电流,即:
I(t)=A。
(3)
实验结果如图6所示。由图6可见,给定伺服采样周期为0.01 s,响应电流围绕在给定的水平幅值附近波动,表明测控系统具有较高的可靠性。
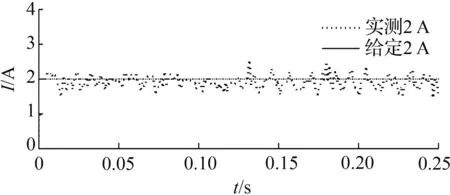
(a)I=2 A
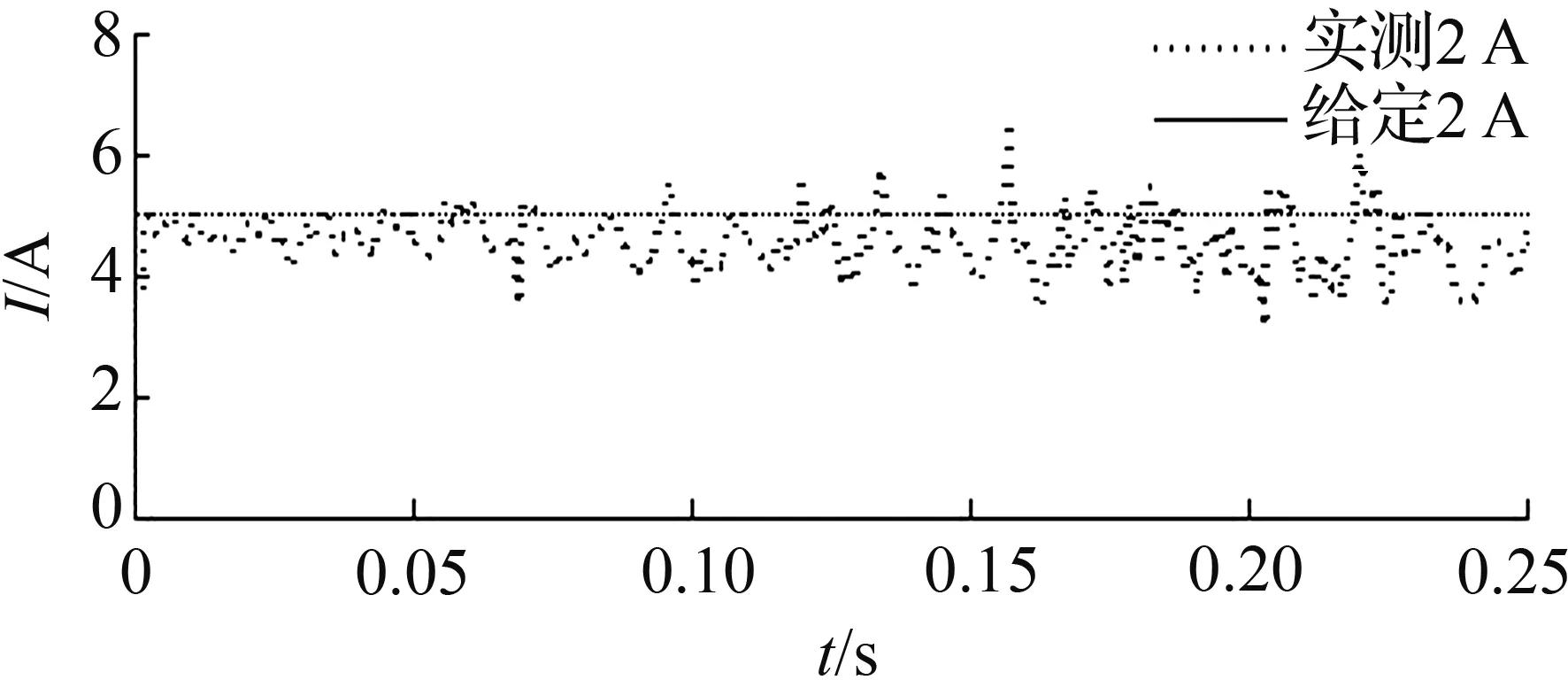
(b)I=5 A
图6 阶跃电流跟踪响应曲线
Fig.6 Tracking curve of step current
2.4 正弦速度跟踪响应实验
通过驱动器给关节驱动电机施加一个按正弦规律变化的速度,即:
v(t)=Asinωt。
(4)
实验结果如图7所示。由图7可见,给定伺服采样周期为0.1 s,速度模式下的速度响应误差大约保持在0.2 s。这表明系统在速度模式下同样具有良好的跟踪能力。
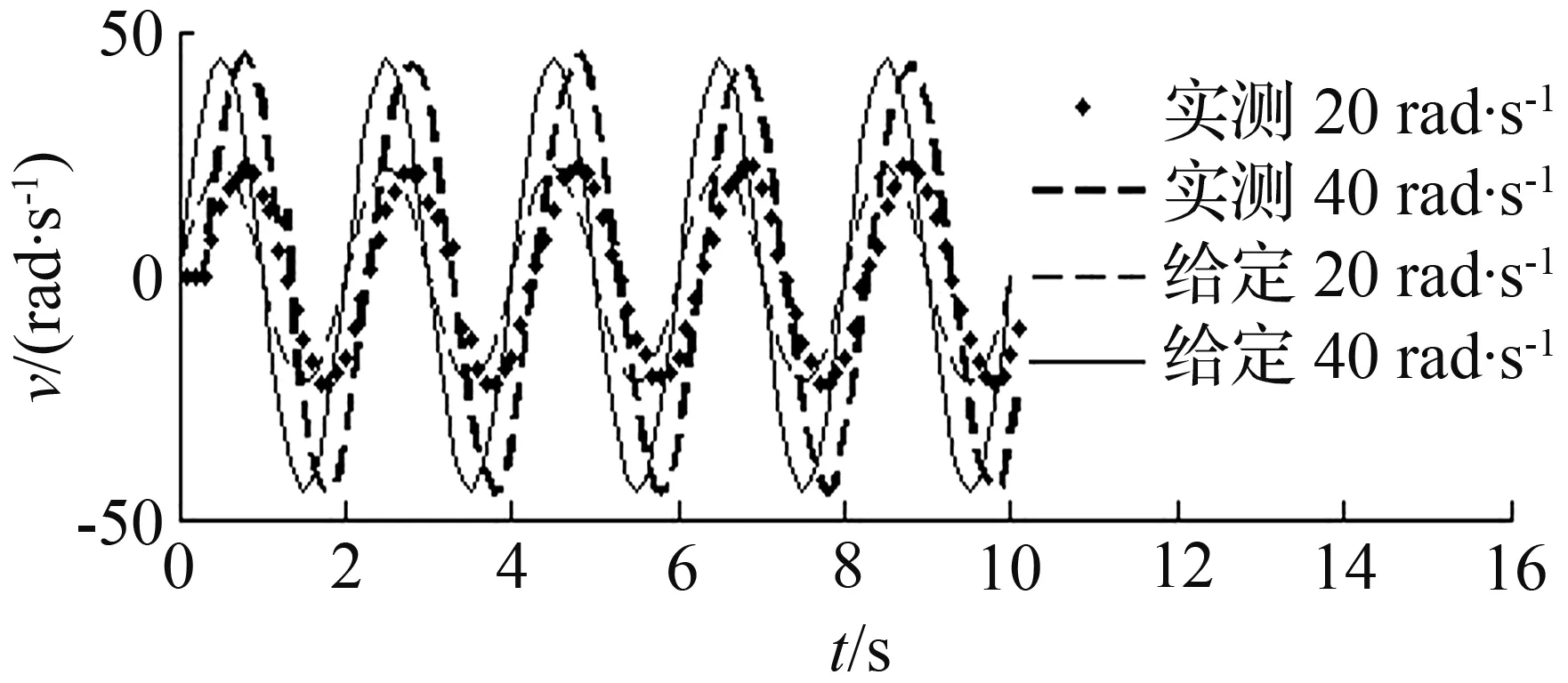
(a)T=2 s
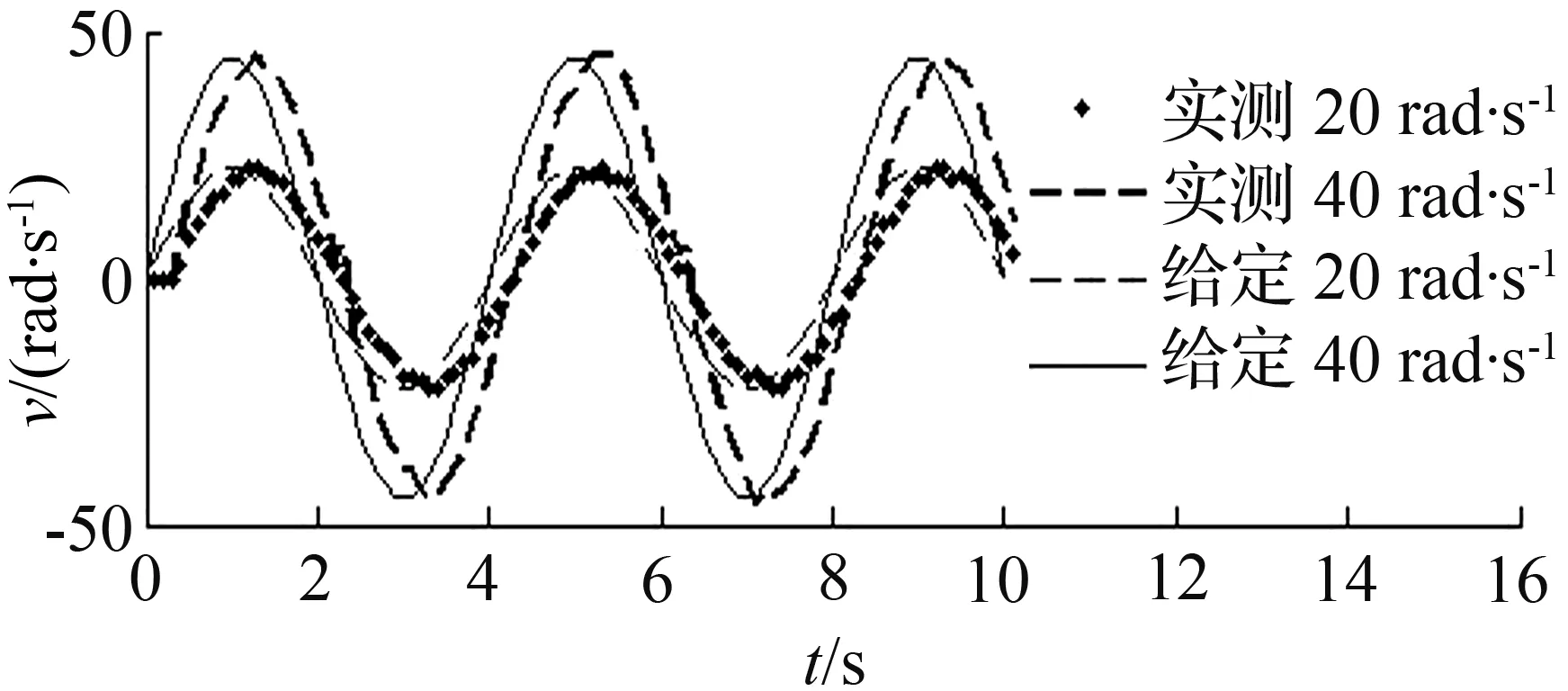
图7 正弦速度跟踪响应曲线
Fig.7 Tracking curve of sine-wave velocity
2.5 衰减速度跟踪响应实验
通过驱动器给关节驱动电机施加一个按指数衰减的速度(伺服采样周期为0.1 s、周期为1 s、幅值为20 rad/s)
v(t)=Ae-σtcosωt,
(5)
式中,σ同样是一个与衰减速率有关的参数。
实验结果如图8所示。由图8可见,响应速度与给定速度保持稳定的跟踪误差,但具有良好的跟踪轨迹。随着σ值的增大,响应速度具有明显的衰减趋势。
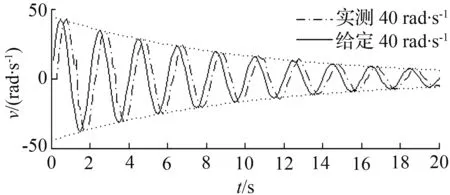
(a)σ=0.1
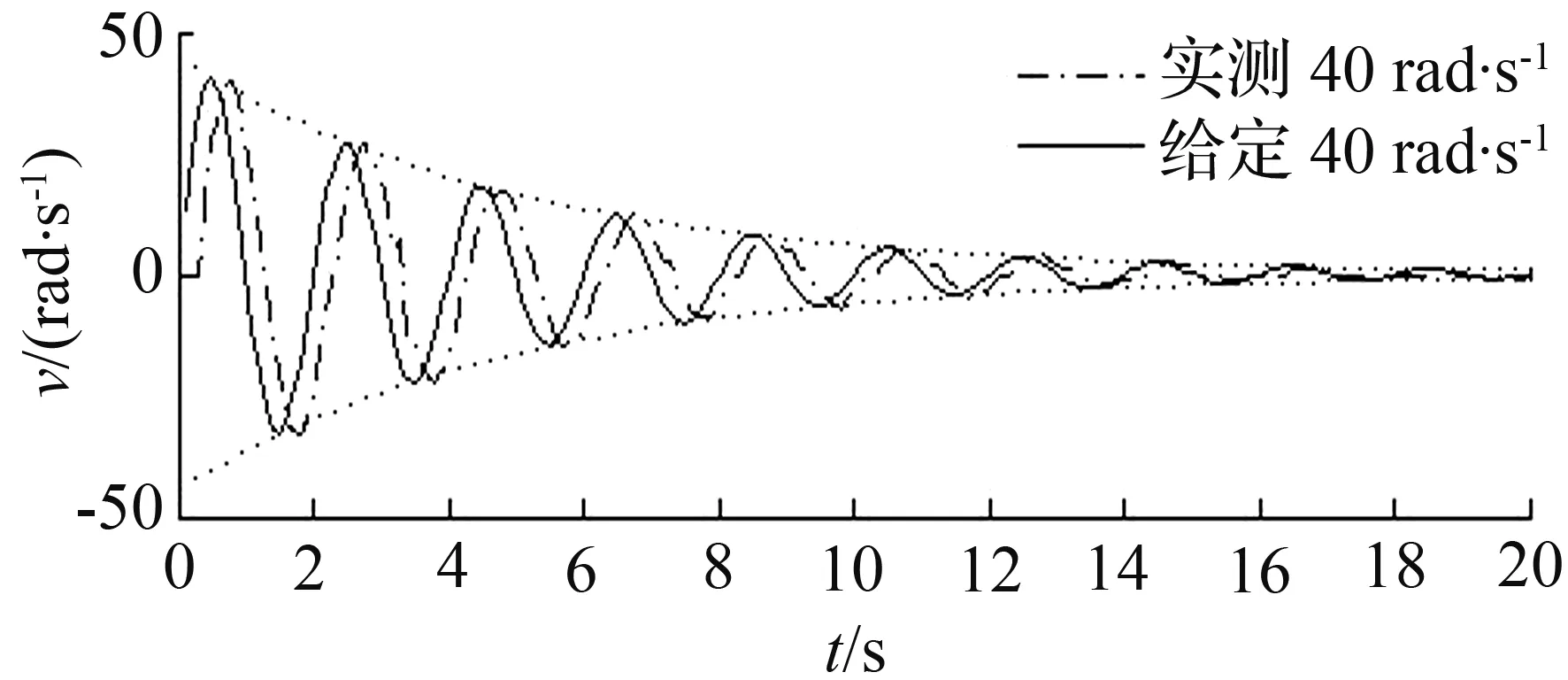
图8 衰减速度跟踪响应曲线
Fig.8 Tracking curve of exponential decay velocity
2.6 电机的力矩辨识实验
由于独轮车机器人测控系统使用的BDMC3610直流电机驱动器不支持直接的力矩模式,因此,本研究通过电流模式实现。而给定的电流能否满足所需力矩的需要是实现控制的重点,因此,为了验证测控系统的可靠性,针对前述的正弦电流(I=Asinωt,周期为4 s)跟踪实验做了进一步的研究。
由摆轮运动产生的角速度可得出摆轮运动产生的角加速度,即:
(6)

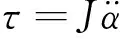
(7)
分别对幅值为4 A、6 A的电流和相应摆轮的计算力矩进行了拟合,结果如图9所示。由图9可见,二者呈明显的线性关系(在大量实验之后,仅给出其中两组实验结果)。忽略线性关系的微小常量偏置,可以得出力矩与电流之间的关系式为:
τ=cTI,
(8)
式中,cT为力矩系数,I为驱动器给定的电机电流。通过大量实验发现,cT取平均值为2.47 Nm/A。
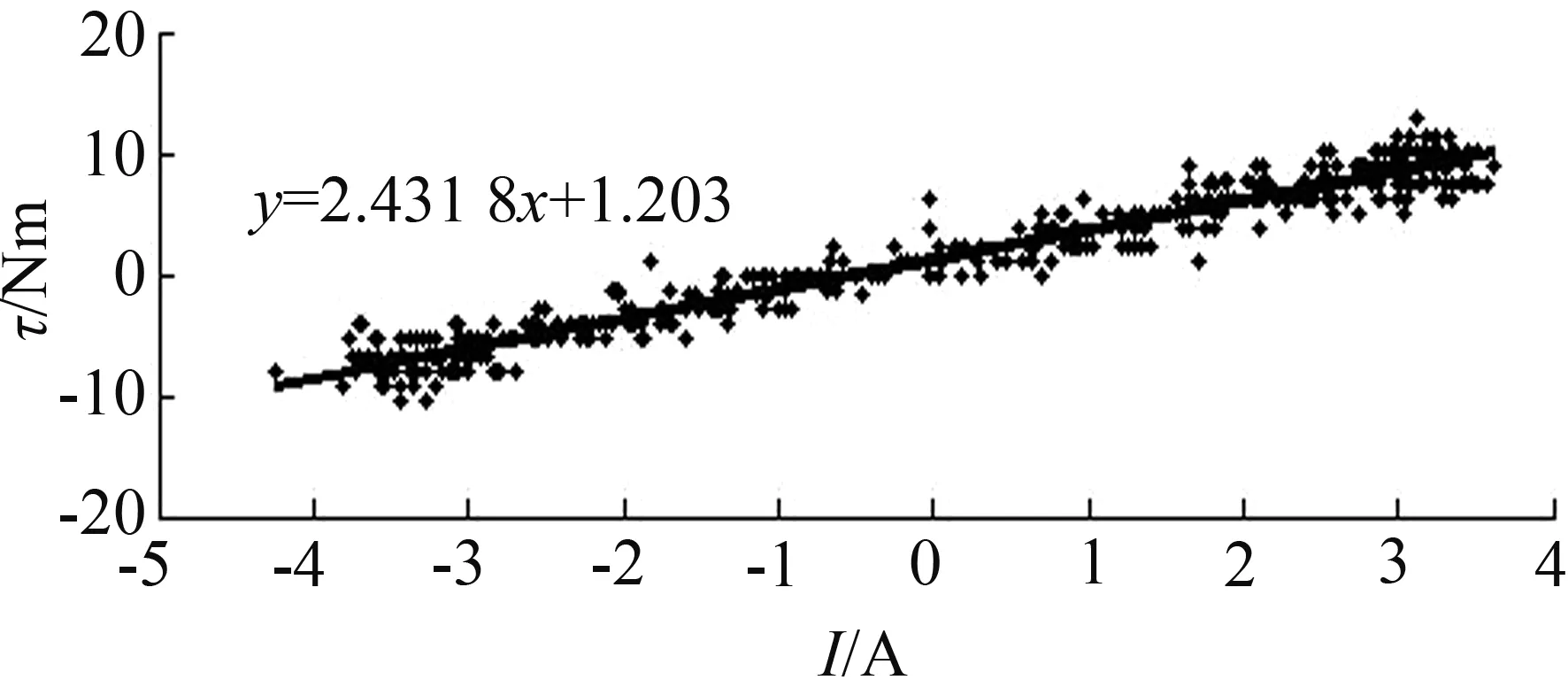
(a)I=4A

图9 电流与计算力矩拟合轨迹
Fig.9 Fitting of current and calculated moment
3 电流与力矩关系的实验验证
通过独轮车机器人行走轮的运动来验证电流与力矩之间的关系,进一步检验该测控系统的可靠性。图10是给定的余弦衰减电流I=Ae-σtcosωt(幅值6 A,周期分别是1 s, σ分别是0.2、0.4)的计算力矩和拟合力矩情况。
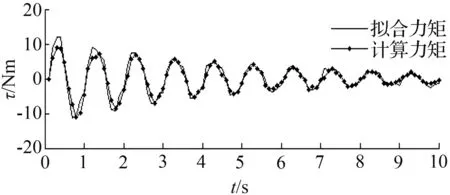
(a)σ=0.2

图10 力矩跟踪曲线
Fig.10 Tracking curve of moment
由图10可见,计算力矩与拟合力矩能较好吻合。这验证了电流与计算力矩拟合的精确。

(9)

图11 力矩偏差Fig.11 Deviation range of moment
力矩偏差如图11所示。由图11可知,期望力矩和拟合力矩的偏差H∈[-3.75,4.09]。通过偏差H可计算出各点的残差平方和为:
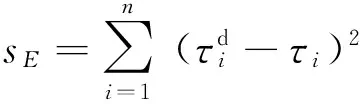
(10)
均方差为:

(11)
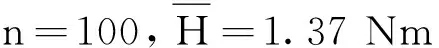

4 平衡控制实验验证
基于前述各种实验的结果,利用独轮车机器人的俯仰平衡运动的控制实验对该测控系统的稳定性和可靠性作进一步验证。
根据基础实验,取电流力矩系数cT为2.47 Nm/A,通过电流模式为电机直接提供较准确的电流,从而间接为平衡控制提供较精确的力矩输出。
具体来说,只考虑独轮车的前后俯仰运动,对独轮车的动力学模型进行了降维,得到一个二维的力学子系统(本研究不对复杂的非线性动力学模型作详细的推导)为:

(12)
式中,Dij和Cij分别为系统质量矩阵D和速度耦合项矩阵C的元素,且有
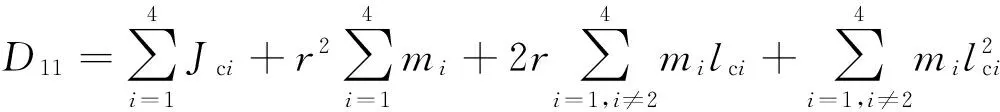
D21=D12,
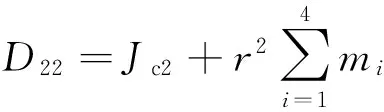

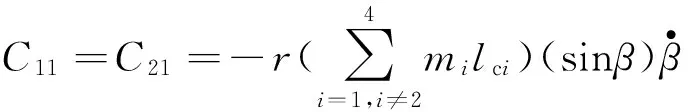
C12=C22=0,
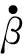

表1 独轮车机器人系统参数
下面利用部分反馈线性化方法设计控制器。
因为D12≠0,由矩阵式(12)的第1式可得:
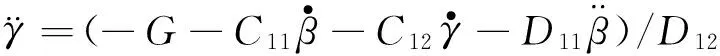
(13)
将式(13)代入式(12)的第2式,得到:
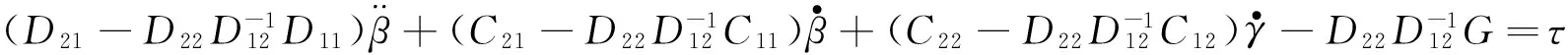
(14)
引入虚拟控制量v,则控制力矩为:

(15)
则系统(12)可以改写为:
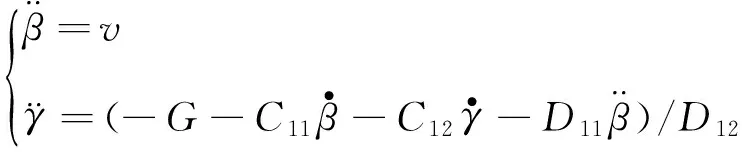
(16)
若选取虚拟控制量为:
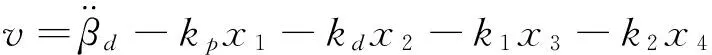
(17)
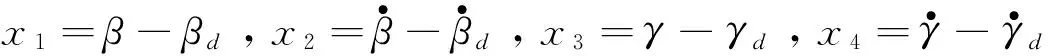

(18)
系统(18)在平衡点(x=0)的Jacobin矩阵为:

(19)
则其特征方程为:
s4+(kd-k2w2)s3+(kp-k1w2)s2+k2w1s+k1w1=0 ,
(20)
式中,w1,w2为系统参数的函数。
根据Routh判据,系统(19)稳定的条件是:

(21)
式(21)表明,选择合理的控制器参数kp、kd、k1和k2,控制力矩式(15)可以实现独轮车俯仰平衡运动。
选取控制参数kp=40,kd=20,k1=0.4,k2=0.15,由式(12)~ (21)可得实验结果如图12~图13所示。




图12 俯仰运动平衡控制实验视频连拍
Fig.12 Video shooting of the pitch balance motion

(a) 俯仰角跟踪曲线

(b) 实测电流与给定电流的比较曲线
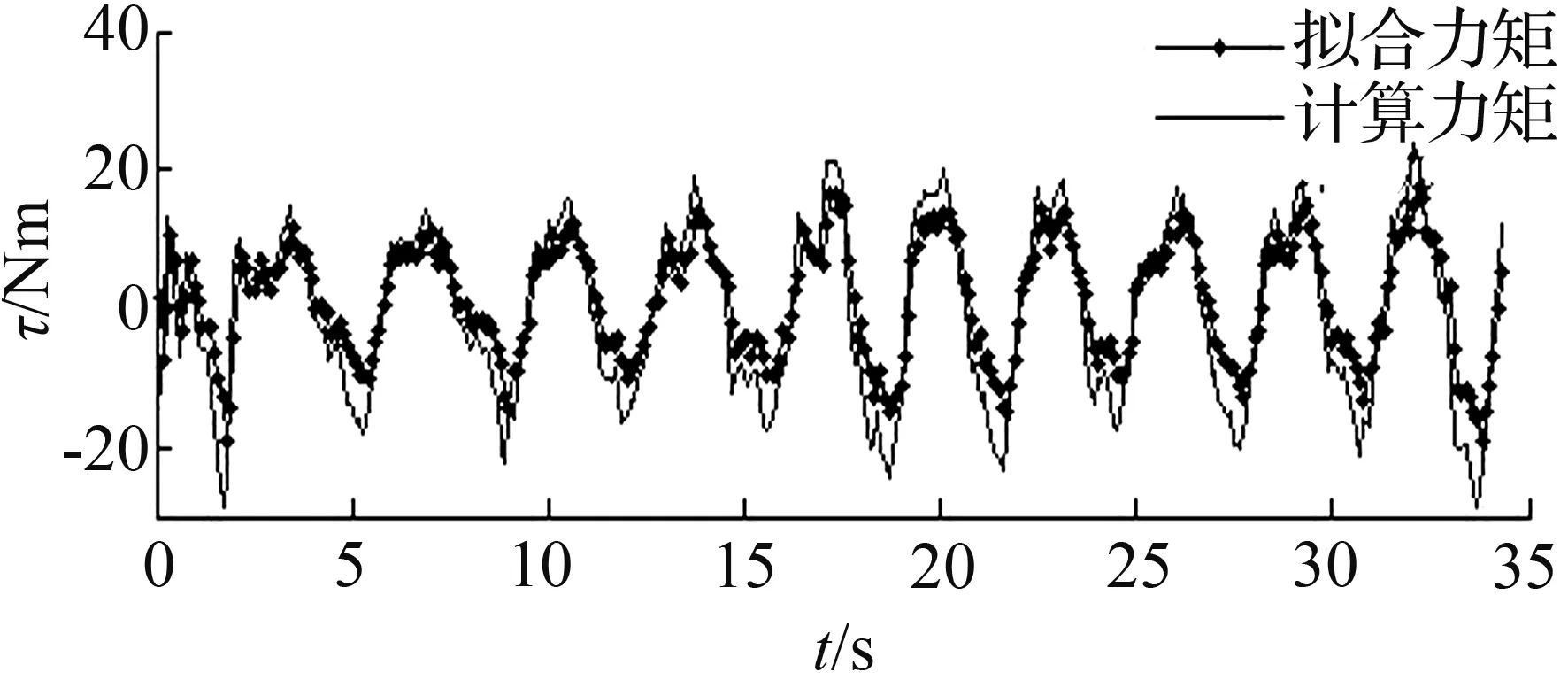
(c) 拟合力矩与计算力矩的比较曲线
从图13(a)可见,给系统引入控制后,车架俯仰角β偏离平衡位置的最大值为0.09 rad(约5.2°),且俯仰角始终围绕平衡点(β=0)处波动,说明独轮车机器人实现了前后俯仰的动态平衡。从图13(b) 可以看出,根据关系式(τi=2.47·I)给定的控制电流的波动形式与俯仰角的波动形式基本吻合,验证了关系式(8)的可靠性。从图13(c) 可以看出,拟合力矩和计算力矩具有较好的吻合曲线,表明在不考虑二者偏差的前提下,由控制器提供的输出力矩能够达到较好的控制效果。
5 结 语
①本研究基于一台3驱动的独轮车平台,开展了驱动关节的电流跟踪和速度跟踪等实验,各种实验的跟踪效果都比较稳定良好。
②实验得出了电流与力矩之间存在明显的线性关系的重要结论(τi=2.47·I),可为独轮车机器人的其他平衡运动提供理论参考。
③作为验证,本研究在搭建的测控系统上单独考虑车体的前后俯仰运动,通过对力学模型进行降维获得一个能够描述独轮车机器人俯仰平衡运动的子系统。采用部分反馈线性化方法,将子系统中的欠驱动车体俯仰角线性化,并选择车体的俯仰角和行走轮的转动角为输出设计了俯仰运动的平衡控制器。最后通过物理样机实验证明了控制器的有效性。
[1] 阮晓钢,胡敬敏,王启源,等.一种独轮车机器人的滑模控制[J]. 控制工程, 2011,18(1):128-132.
[2] 朱晓庆,阮晓钢,魏若岩.基于惯性飞轮的独轮自平衡机器人侧向动力学分析[J]. 应用力学学报, 2013,30(3): 395-400.
[3] LEE J H, SHIN H J, LEE S J,et al.Novel air blowing control for balancing a unicycle robot[J]. Intelligent Robots and Systems, 2010: 2529-2530.
[4] 郭磊,廖启征,魏世明,等.独轮车机器人的动力学建模与非线性控制[J]. 系统仿真学报, 2009,21(9): 2730-2733.
[5] 庄未,江汉,刘成举,等.一种独轮车机器人测控系统的设计与实现[J]. 测控技术,2015,34(9):69-72,75.
[6] 庄未,黄渭,黄用华.独轮车机器人的欠驱动力学特性与平衡控制策略[J]. 机械设计,2013, 30(6):18-2.
[7] SCHOONWINKEL A.Design and test of a computer stabilized unicycle[D]. Palo Alto,USA: Stanford University, 1987.
[8] VOS D W.Nonlinear control of an autonomous unicycle robot: practical issues[D]. Cambridge:Massachusetts Institute of Technology, 1992.
[9] 丛秋波.村田制造所:“村田顽童”携手“村田婉童”展示高新技术[J]. 电子设计技术, 2008 (12): 124-125.
[10]庄未,刘成举,江汉,等.一种独轮车机器人的动力学建模及俯仰平衡控制[J]. 中国机械工程,2016,27(4):1-7.
[11]庄未,江汉,刘成举,等 一种独轮车机器人俯仰平衡运动的控制与实现[J]. 计算机测量与控制,2016,24(1):122-125.
[12]阮晓钢,胡敬敏,蔡建羡,等.一种基于模糊控制理论的独轮机器人控制算法[J]. 控制与决策,2010,25(6):862-866.
[13]阮晓钢,王启源,胡敬敏,等.一种独轮机器人系统及其控制方法: 中国,101590323 [P]. 2009-12-02.
[14]王启源.独轮自平衡机器人建模方法与控制研究[D]. 北京:北京工业大学, 2011.
[15]胡泽岩.独轮车机器人的动力学建模与控制[D]. 北京:北京邮电大学,2015.
[16]冯俊杰.多机器人系统避障与最优协调[D]. 南宁:广西大学,2014.
(责任编辑 裴润梅)
Analysis and experiments on driving joints characteristic of the unicycle robot
ZHUANG Wei, JIANG Han, ZHU Gan-min, HE Shu-tong, ZHANG Fan
(School of Mechanical and Electrical Engineering,Guilin University of Electronic Technology, Guilin 541004,China)
In order to study driving joints characteristic, a research on joint-driving motors of a unicycle robot with three actuators is explored through diverse methods. The methods used include the current tracking response (sinusoidal, exponential decay and step), velocity tracking response (sinusoidal and exponential decay), identification of the relationship between the current and the torque and the balance pitching motion control of the robot. Results show that driving joints’ tracking response to different current and velocity curve lags in time domain but possesses fine dynamic performance in amplitude and frequency. In addition, there is a harmonious relationship between the current and the output torque. By using those relationships a PD controller based on the partial feedback linearization for robot’s balance pitching motion is designed. Therefore, the research proves that the driving joints characteristic plays a significant role in balance control of the robot system. Furthermore, it provides a theoretical reference for other balance motions of the unicycle robot.
unicycle robot; driving joints characteristic; partial feedback linearization
2016-04-13;
2016-06-01
国家自然科学基金资助项目(51305087);国家级大学生创新创业训练计划项目(201510595034);桂林电子科技大学研究生教育创新计划资助项目(YJCXS201511、YJCXS201512)
庄 未 (1977—),女,黑龙江哈尔滨人,桂林电子科技大学副教授,博士;E-mail:zhangweibupt@sohu.com。
庄未,江汉,朱赣闽,等.独轮车机器人驱动关节特性的分析及实验研究[J].广西大学学报(自然科学版),2016,41(5):1514-1523.
10.13624/j.cnki.issn.1001-7445.2016.1514
TP242
A
1001-7445(2016)05-1514-10

