基于两种算法的无线信道“指纹”特征识别*

王瑞星，刘　斌，杜健鹏，李　明

（1.中国工程物理研究院研究生院，北京 100088；2.中航工业西安航空计算技术研究所，陕西 西安 710068）

基于两种算法的无线信道“指纹”特征识别*

王瑞星1，刘斌1，杜健鹏1，李明2

（1.中国工程物理研究院研究生院，北京 100088；2.中航工业西安航空计算技术研究所，陕西 西安 710068）

针对无线信道“指纹”特征建模，包括“指纹”特征参数的建立、匹配识别、连续特征参数的“区域划分”等问题，用无线信道参数的提取算法、BP神经元网络算法和建立的微元试探法对模型进行分析求解。数值实验结果表明，矩阵奇异值分解和ESPRIT这两种无线信道参数提取算法对不同场景提取的参数能够进行很好地区分，BP神经元网络算法也能够准确识别场景和样本模式，利用微元试探法对连续信道区域的划分也证明是足够精确的。

无线信道；指纹；BP神经网络；微元试探法；特征识别

0　引 言

移动通信产业一直以惊人的速度迅猛发展，已成为带动全球经济发展的主要高科技产业之一，并对人类生活及社会发展产生巨大影响。在移动通信中，发送端和接收端之间通过电磁波来传输信号，我们可以想象两者之间有一些看不见的电磁通路，并把这些电磁通路称为无线信道。无线信道与周围的环境密切相关，不同环境下的无线信道具有一些差异化的特征。如何发现并提取这些特征并将其应用于优化无线网络，是当前的一个研究热点。类比人类指纹，我们将上述无线信道的差异化的特征称为无线信道“指纹”。无线信道“指纹”特征建模，就是在先验模型和测试数据的基础上，提取不同场景或不同区域内无线信道的差异化的特征，进而分析归纳出“指纹”的“数学模型”，并给出清晰准确的“数学描述”。

当前，无线信道的识别算法主要有以下三类。

第一类是谱估计算法，常见的是Schmidit［1］提出的多重信号分类法（Multiple Signal Classification，MUSIC）。它可以对入射波波前数目、到达方向或发射方向、入射波形的强度和互相关提供渐进的无偏估计。然而，由于该算法对于参数空间搜索的计算量和存储量较大，且当入射信号为相干信号时，MUSIC算法无效。因此，文献［2］提出了新的算法以对相干信号进行方向估计，表现出了更高的精度，且能在低信噪比时准确估计入射信号的数目。

第二类算法是参数子空间估计法。这类算法最主要的是在文献［3］中提出的旋转不变技术估计信号参数算法（Estimating Signal Parameters via Rotational Invariance Techniques，ESPRIT）。它利用信号子空间的旋转不变特性，可以用于水平角的准确参数提取。

第三类算法是基于最大似然估计算法（Maximum Likelihood Estimation，MLE）而产生的迭代的期望最大算法（Expectation Maximization，EM）［4-5］。它可以实现对时延、水平角、幅度的联合估计。文献［6］对EM算法进行了推广，得到了空间交替广义期望最大算法（Space-Alternating Generalized Expectation Maximization，SAGE）。SAGE算法可以同时对时延、离开角、到达角、多普勒频移、幅度等多位参数进行联合估计。

此外，韩彩的硕士学位论文［7］应用前三类无线信道参数提取方法研究了高速铁路场景；高远在其硕士学位论文［8］中应用SAGE算法，对无线信道带宽参数进行了研究。

本文的结构如下：第1节给出了无线信道的研究背景及其参数提取原理；第2节对待研究的内容进行详细分析；第3节给出了无线信道识别的两种算法，并建立具体的模型；第4节给出所研究问题的结论；第5节对所建立的模型进行简单的评价。

1　背景描述

在典型的无线信道中，电磁波的传输不是单一路径，而是由许多因散射（包括反射和衍射）而形成的路径构成。由于电磁波沿各条路径的传播距离不同，因此相同发射信号经由各路径到达接收端的时间各不相同，即多径的时延间存在差异。此外，各条路径对相同发射信号造成的影响各不相同，即多径的系数之间存在差异，如图1所示。

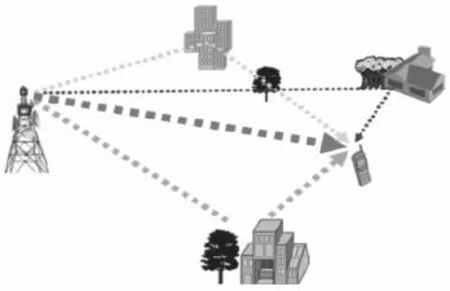
图1　电磁波传输路径

工程上，考虑到多径系数及多径时延的影响，在保证精度的前提下，可以用“离散线性系统”为无线信道建模。需要注意的是，该模型中的信号及多径系数均为复数。理想信道测量可以理解为获取该系统的单位序列响应，即获取单位脉冲δ（k）经无线信道传输后被接收到的信号，如图2所示。

图2　理想信道测量模型

上述理想信道测量的结果用公式表述如下：

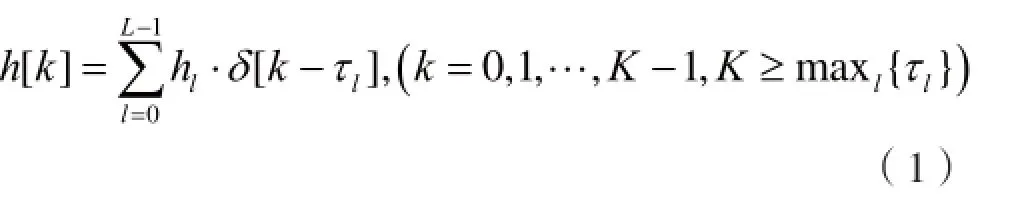
这里，k为离散信号的样点标识，假设共有K个样点；L是当前时刻的路径总数；hl为当前时刻第l条路径上的信道系数，通常是复数；τl为当前时刻第l条路径的时延，且已折算成样点数，即延迟了“τl”个样点。

显然，复信号h［k］给出了当前时刻的完整信道。需要强调的是，上述各个参数包括hl、τl和L，都会随着时间变化而变化，即各个参数具有时变性。相应的，h［k］的功率在信号波长λ的量级上会出现时而加强时而减弱的快速变化，称之为多径衰落或小尺度衰落。同时，快速变化的功率的平均值也会出现缓慢变化，主要是由于周围环境或气象条件的改变而引起，称为阴影衰落或大尺度衰落。两种衰落特征如图3所示。

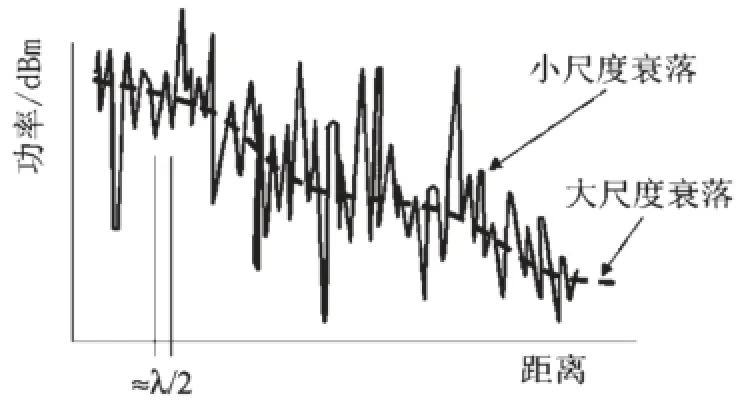
图3　阴影衰落和大尺度衰落

上述理想信道测量的结果h［k］是无法直接获取的。因为在真实无线通信系统中，为了改善信号的传输质量，通常需要在系统的发射端和接收端各增加一个滤波器。所有滤波器在真实信道测量中的影响，可以等效用函数g［k］来表示。此时，信道测量的结果为：

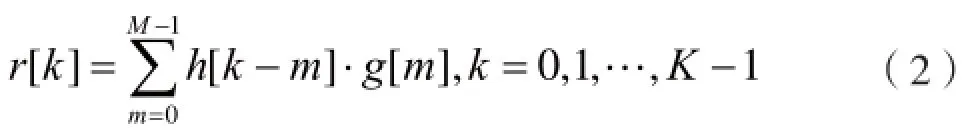
其中，M为滤波器的长度，即g［k］的样点数。

考虑到信道的时变性和实测中引入的噪声，不同时刻的真实信道测量结果及其对应的无线信道分别为：

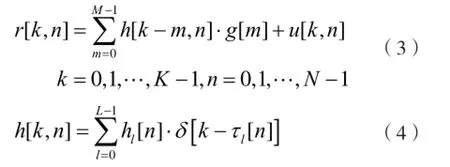
其中，n表示测试的样本标识，对应测试时刻，这里假设共有N个样本；hl（n）表示n时刻第l条路径上的信道系数，通常是复数；τl（n）表示n时刻第l条路径时延的样点数；u［k,n］表示n时刻第k个测试样本上引入的复高斯白噪声；r［k,n］表示n时刻单位脉冲一次经发送滤波器、信道和接收滤波器后的实际接收信号，是k和n的二元函数。显然，可以从r［k,n］中获取完整的指纹信道h［k,n］。

为了便于理解，图4给出了不同时刻下无线信道的示意图，同时也给出了样本标识n和样点标识k的相互关系。容易发现，不同时刻下多径的条数、时延以及系数值都有可能发生变化。直观上，变化的参数都含有一些场景化的特征，即上述不同参数的变化都可能存在一定的规律。

基于上述或更多的参数及特征，一个场景或一定区域内的无线信道可能存在一定的“指纹”。利用所定义的“指纹”进行场景分析及无线网络优化，具有重要的意义。

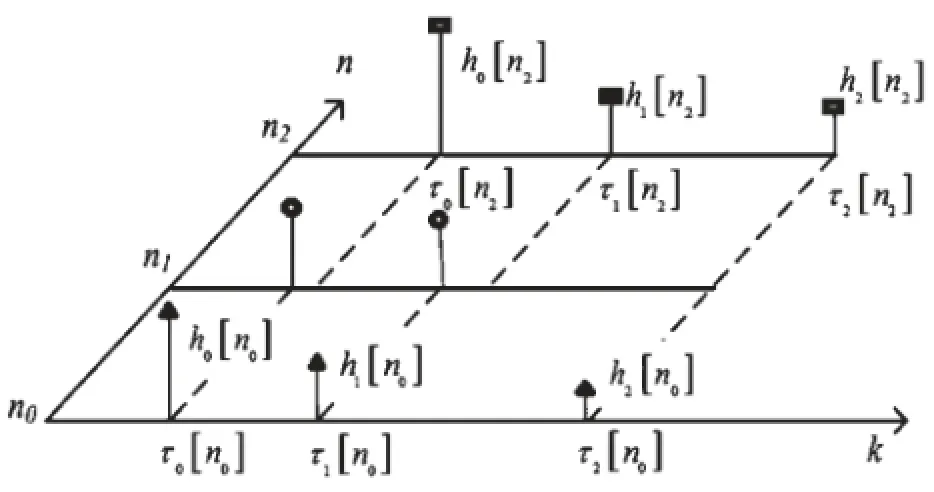
图4　不同时刻下的无线信道

2　待研究内容分析

2.1问题一分析

本研究旨在挖掘、提炼和聚合实测信道数据中的各种特征，用数学的语言描述“指纹”，并验证其在不同场景或不同地理位置下的适用性。

搜集的试验数据中，提供了三种场景的真实信道测量结果。基于三种已知场景的测量结果，将采用特征提取的方法，对所提供的样本加以分析，并给出无线信道“指纹”的模型。

在理想情况下，要想完美区分三个场景，信道测量数据应该越多越好，即在足够还原场景特征信息的前提下，采样的离散数据越多，还原的场景可信度越高。三种场景的真实信道测量结果的形式是N×K维的矩阵，类比于图4，指纹上的点表示在指纹上的采样点，每个采样点都有自己的二维坐标和值。但是，对过多的点进行数据采集是不现实的，不仅浪费存储空间，还影响数据比对效率。所以，本文将从较大的采样矩阵中抽取有限个表征矩阵特性的特征参量作为无线信道“指纹”。从矩阵角度，可以用奇异值分解算法［9］得到矩阵的奇异值。不同场景下，得到不同结构的信号矩阵对应的唯一的奇异值向量。实际上，这里的奇异值与无线通信中多重信号分类（Multiple Signal Classification，MUSIC）算法［1］提取的空间方位谱存在对应关系；从无线通信的角度，可以用无线信道参数萃取算法，包括旋转不变技术估计信号参数ESPRIT（Estimation of Signal Parameter via Rotational Invariance Techniques）算法［3］提取噪声方差、时延、离开角、到达角、多普勒频移、复振幅等参数。两种特征值抽取算法的性能特点为：矩阵奇异值所对应的MUSIC算法是一种高分辨率的高精度的无线信道参数估计算法，而ESPIRT算法在有效性和稳定性方面有突出的表现［7］。

2.2问题二分析

试验数据还提供与问题一中某些场景相对应的二个真实信道测量结果。基于问题一中所提供的三个场景以及建立的“指纹”模型，如图5所示，可以识别出此处提供的二个样本分别属于哪个场景。

图5　指纹识别

基于问题一中已经建立的指纹模型和评价指标，这里判别两个样本属于哪个场景，本质上就是进行模式识别。本文将采用BP神经元网络算法进行模式识别［10］。

2.3问题三分析

另一组试验数据提供了一条连续路段的真实信道测量结果。该结果对应于以3 km/h的速度步行近150 m的测试距离。该路段可能包含不同的场景或环境，对应不同的“指纹”特征。基于第一个问题的方法，本文将其进行合理分段，并给出分段的“指纹”分析。理论上，区域划分越细，后续做区域识别的精确程度越高，但过细的区域划分会在“指纹”特征中引入更多错误，导致误判概率增大。

由于所给数据是一个连续区域，因此基于实际物理常识选取一个“微元”，然后通过类似于试探搜索的方法进行不等距区域划分，同时建立一个最优划分的评判函数来评判划分效果，并给出最优划分结果。

2.4问题四分析

最后一个试验数据提供了二个真实信道测量结果。基于问题三中的区域划分和问题一中的评价指标，本文首先通过无线信道参数提取算法给出该数据的信道“指纹”，然后利用模式识别算法和建立的评判标准进行信道识别，并判断此处提供的二个样本是否采集自问题三中所提供的路段。

3　两种算法和模型建立

3.1基于无线信道参数提取算法的“指纹”模型和“评价指标”

3.1.1矩阵奇异值分解和旋转不变技术估计信号

矩阵的奇异值分解算法是一种较为简单的算法，这里不做具体介绍，详细过程可参考文献［9］。一般选用MATLAB工具箱自带的SVD函数求解即可。

ESPRIT算法在有效性和稳定性方面都有非常突出的表现，已经被公认为空间谱估计的一种经典算法。下面简单介绍ESPRIT算法［3］。

首先，把K×N的二维矩阵r［k,n］分解成两个子阵，分别为：

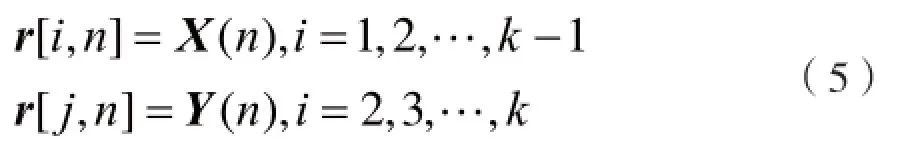
其中这两个子矩阵可以表示为：

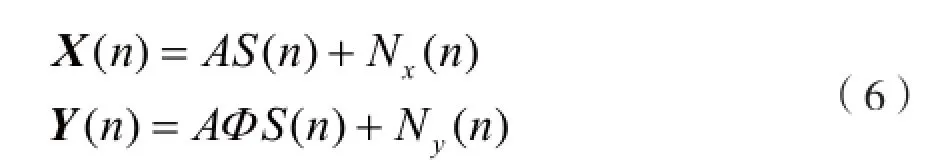
子矩阵1接收的信号矩阵为X（n），输出噪声为Nx，子矩阵2接收的信号矩阵Y（n），输出噪声为Ny。它们都为均值为0的高斯白噪声，且相互独立，满足下式：

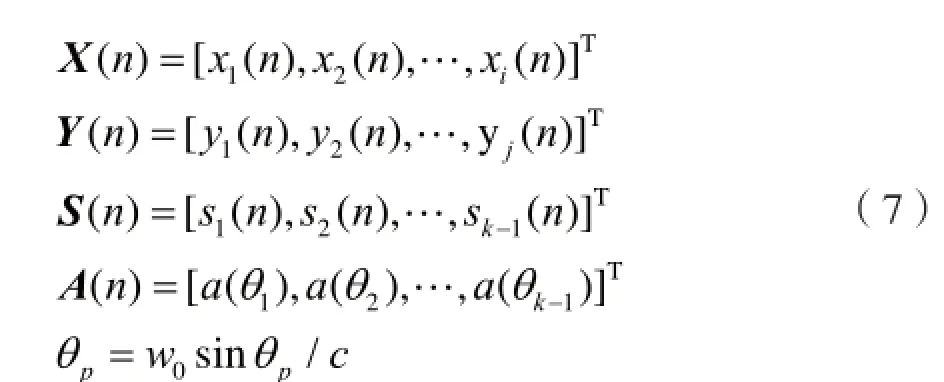
其中：

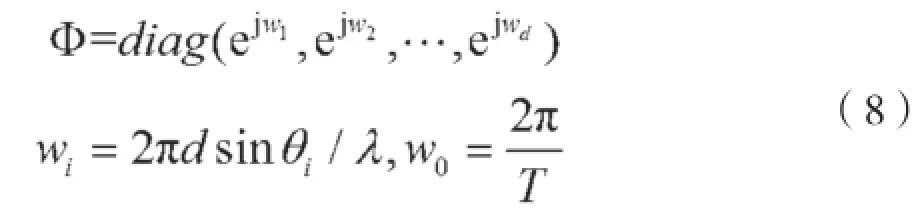
这里，T是发射脉冲的周期；Y相当于X经过旋转得到，可以将Φ称为旋转矩阵。

于是，矩阵的自相关矩阵与两个矩阵之间的相关矩阵可以表示为：

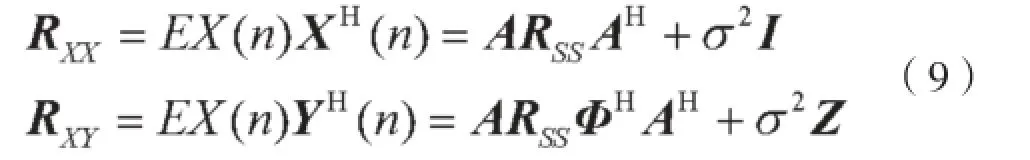
式中I为单位矩阵，Z相当于把单位矩阵上对角线的1下移，可以表示为：

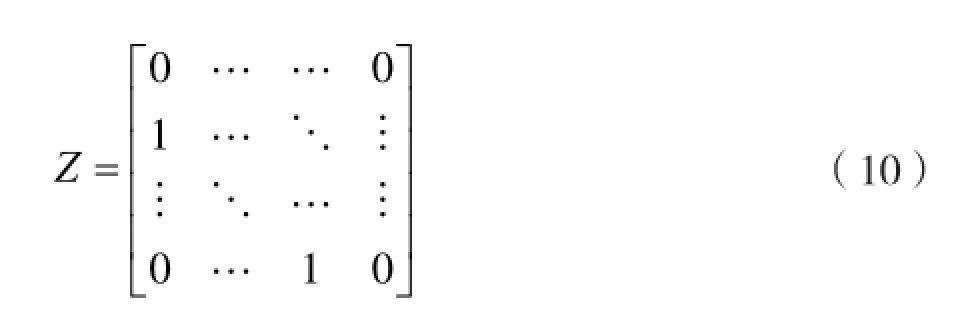
σ2可以对RXX进行特征值分解得出，所以协方差矩阵：

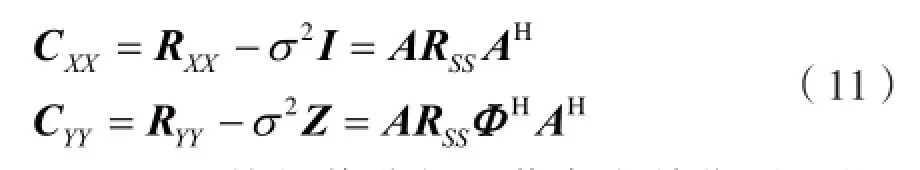
CXX和CYY特征值分解，若存在单位圆上的d个特征值，则可得出波方向的入射角。通过上述分析可知，ESPEIT算法的优点在于它可以不通过复杂的空间搜索来计算来波到达角，从而减少计算量，且节省了存储空间，更便于硬件实现，且可以得到噪声方差。

3.1.2“指纹”模型和“评价指标”建立

根据上述分析，ESPRIT算法萃取噪声方差和到达角的流程如图6所示。

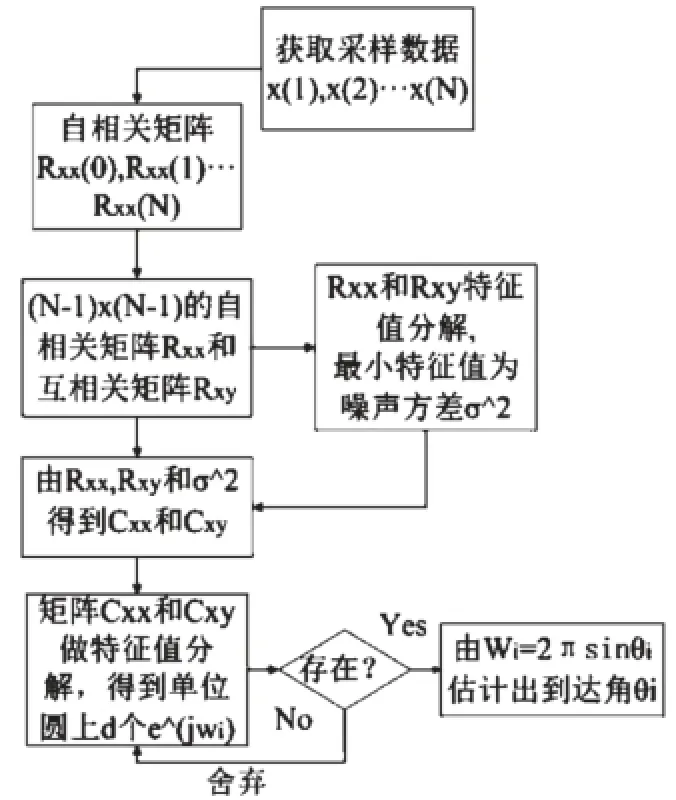
图6　ESPRIT算法流程

（1）首先获取一定的接收端数据采样值x（1）,x（2）,…,x（N），进而估计输入信号的自相关矩阵RXX（0）,RXX（1）,RXX（N）。

（2）由步骤（1）估计的自相关函数构造子阵空间，1到N-1为第一个子阵，2到N为第二个子阵，从而求得（N-1）×（N-1）自相关矩阵RXX和（N-1）×（N-1）互相关矩阵RXX。

（3）对自相关矩阵RXX和互相关矩阵RXX进行特征值分解，其中最小特征值为噪声方差σ2的估计值。

（4）利用公式计算CXX=RXX-σ2I和CYY=RYY-σ2Z。

（5）对矩阵CXX、CYY作特征值分解，若存在单位圆上的d个特征值ejwi，则通过wi=2πd sinθi/λ求出估计的到达角值θi；否则，舍弃到达角参数。

经过上面的步骤至少可以得到噪声方差特征参数，即至少可以提取无线信道“指纹”的一项特征。

3.2基于BP神经元网络算法的“场景识别”

3.2.1BP神经元网络算法

神经网络是对人脑或自然神经网络的若干基本特性的抽象，是一种基于连接假说构造的智能仿生模型。人们试图通过对它的研究最终揭开人脑的奥秘，建立起能模拟人脑功能和结构的智能系统，从而使计算机能够像人脑那样进行信息处理。本文主要基于BP神经元网络算法进行模式识别［10］。

以三层BP网络为例。它的结构如图7所示，包含一个输入层、一个隐含层和一个输出层，分别由n,p,q个神经元组成。

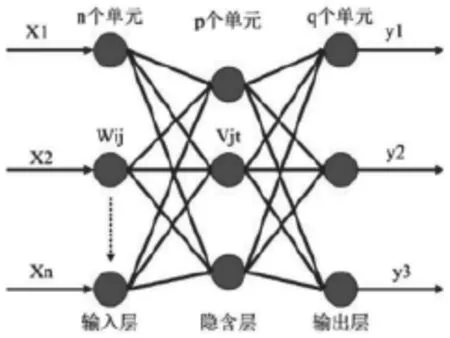
图7　BP神经网络结构

该神经元网络的隐含神经元的输出为：

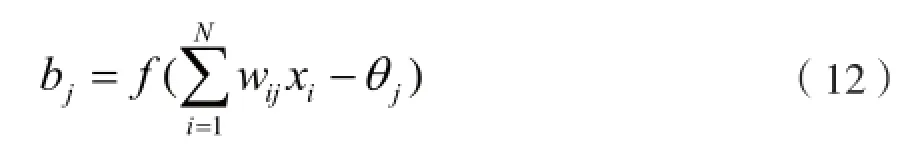
输出层神经元的输出为：

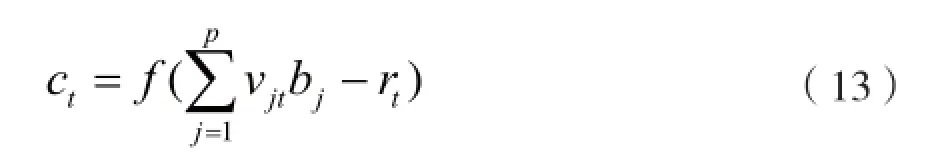
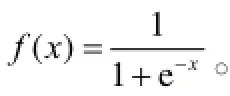
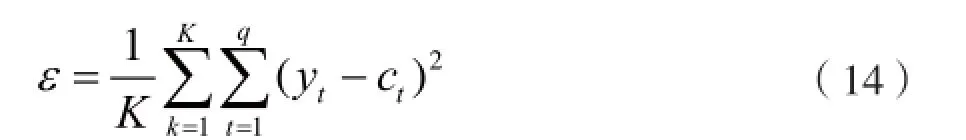
连接权的修正依据反向传播梯度下降法。

（1）隐含层和输出层神经元之间的连接权vjt的修正量为：

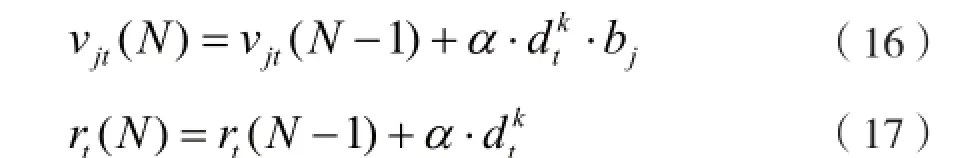
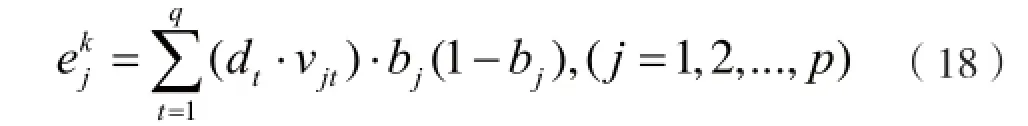
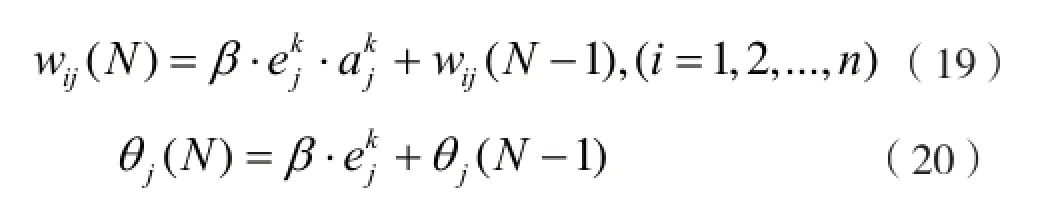
每个样本学习结束，调整相应的连接权值，直到误差函数达到限定值时，判断全局输出误差函数是否到达设定收敛限定值。直到误差函数达到限定值，网络训练结束；否则，如果在达到最大学习次数时误差任然大于设定的数值，训练也结束，网络训练失败。

3.2.2“场景识别”模型建立

利用神经网络进行模式识别的基本步骤：首先根据待识别模式建立所需神经网络，然后利用待识别模式训练神经网络，最后是测试神经网络。依据BP神经网络的基本结构和规则，本文利用MATLAB编写神经网络进行训练和测试，以实现图形的识别。

第一步：根据基于无线信道参数提取算法的“指纹”模型和“评价指标”，给出信道特征参数向量，即输入模式，形式如下：

Xi=［特征参数1,特征参数2,…］

其中角标i表示第i个场景。若共有N个场景，则i=1,2,…,N。

实际上，提取的特征参数是有限的。为了充分利用神经网络，Xi的元素个数可用常数补齐，即：

Xi=［特征参数1,特征参数2,…,γ,…,γ］

这里，常数γ一般取1或0。

考虑到特征参数值的量级有可能相差很大，从而给模式识别带来不必要的误差，于是对向量中的特征参量进行同量级化处理，实际上相当于给特征参数换单位。这不会影响模式识别的效果，形式如下：

X1=［特征参数1/a,特征参数2/b,特征参数3/c，…,γ,…,γ］

X2=［特征参数1/a,特征参数2/b,特征参数3/c，…,γ,…,γ］…… ……

XN=［特征参数1/a,特征参数2/b,特征参数3/c，…,γ,…,γ］

这里,a、b、c根据特征参数的实际取值选取，只要能将特征参量同量级化即可。

第二步：根据要识别的场景个数确定输出模式的个数。例如，问题一中要识别场景个数为3，则可以建立3个输出模式：

“场景1”（模式1）：Y1=［1,0,0］T

“场景2”（模式2）：Y2=［0,1,0］T

“场景3”（模式3）：Y3=［1,0,1］T

当然，如果要识别的“场景”（模式）个数增加，只需增加矩阵元素个数即可表示更多的模式。

第三步：确定神经网络的结构参数。例如，可以利用输入模式和输出模式的个数，确定神经网络中输入层、隐含层、输出层的神经元个数。

如果输入向量元素个数为16，则输入层神经元个数n=16，输出模式个数为3，则输出层神经元个数q=3，中间层神经元个数取n、q中间的数即可，这里可以取p=8。一般情况下，网络的最大容许误差εmax=0.01，学习系数α和β取0.01，网络最大学习次数取为100，该神经网络即可很好地识别不同的模式。最后，利用建好的神经网络进行模式识别。整个模式识别建模的步骤流程如图8所示。

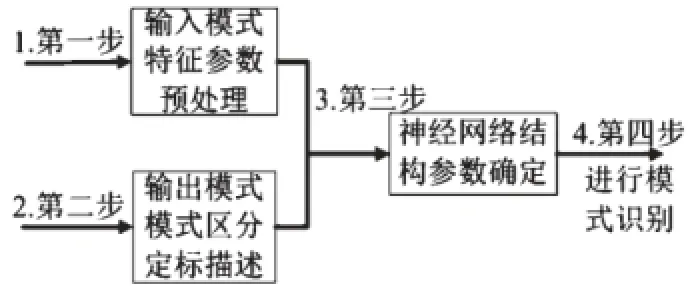
图8　模式识别流程

3.3微元试探算法的区域划分实现

在对题目中第三问进行求解时，采用了微元试探法。由于该算法由笔者建立，故只用作该问题的求解。

具体的，算法如下：

（1）定义计数器c1=1,c2=1以及误差矩阵μ［c1］和分割点矩阵R［c2］。根据微元，假设确定初始步长i。tol为评判误差参数（初始取为1）。

（2）X［i］=f提（r［k,i］）,p=i；X［i+p］=f提（r［k,i+p］）；f提为无线信道提取算法的提取过程函数。

（7）更新tol=tol+0.05进行外循环，即返回第（2）步。当tol＞2.7（tol＞2.7时，已基本不能对区域进行划分），结束外循环。

4　问题求解

4.1问题一求解

根据建立的无线信道特征参数提取算法，包括矩阵奇异值分解算法、旋转不变技术信号参数（ESPIRT）算法，提取每个场景的无线信道特征参数向量。特征参数向量中包括矩阵[,]k nr的奇异值、噪声方差2σ。

首先，为了方便数据包的调用，分别对三个场景中五组数据进行重命名，如下：

［场景i，第j组数据］→“testij”

i=1,2,3； j=1,2,3,4,5

然后，调用程序（从对每个场景的五组数据平均值的矩阵中提取特征参数），生成无线信道特征参数向量（无线信道参数“指纹”）。

结果如表1所示。

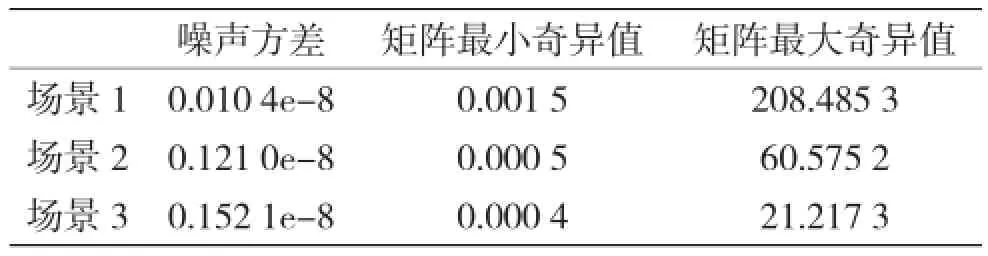
表1　矩阵奇异值分解联合ESPRIT算法提取结果

4.2问题二求解

首先，由矩阵奇异值分解算法联合ESPIRT算法进行无线信道参数提取，得到无线信道特征参数向量Xi=［特征参数1，特征参数2，特征参数3］，即表1中的数据。根据“场景识别”模型建立的方法，且为了充分利用神经网络性能，γ取1，补足参数向量元素为16个。对特征参数向量同量级化处理a=1e-9,b=1e-3,c=1e3。

其次，对三个场景进行模式标定，即：

“场景1”（模式1）：Y1=［1,0,0］T

“场景2”（模式2）：Y2=［0,1,0］T

“场景3”（模式3）：Y3=［1,0,1］T

最后，确定神经网络三个结构层神经元的个数。输入层神经元个数n=16，则输出层神经元个数q=3，中间层神经元个数p=8，其他结构参数取“场景识别”模型建立中的默认值。数值试验中，提供与之前三个场景中某些场景对应的两个真实信道测量结果即两个样本，然后判断这两个样本分别来自哪个场景。因此，对三个场景和两个样本分别提取各自的无线信道特征参数向量，然后把处理后的无线信道特征参数向量X1（场景1），X2（场景2），X3（场景3），X4（样本1），X5（样本2）带入程序中进行初始化，运行的结果如表2所示。

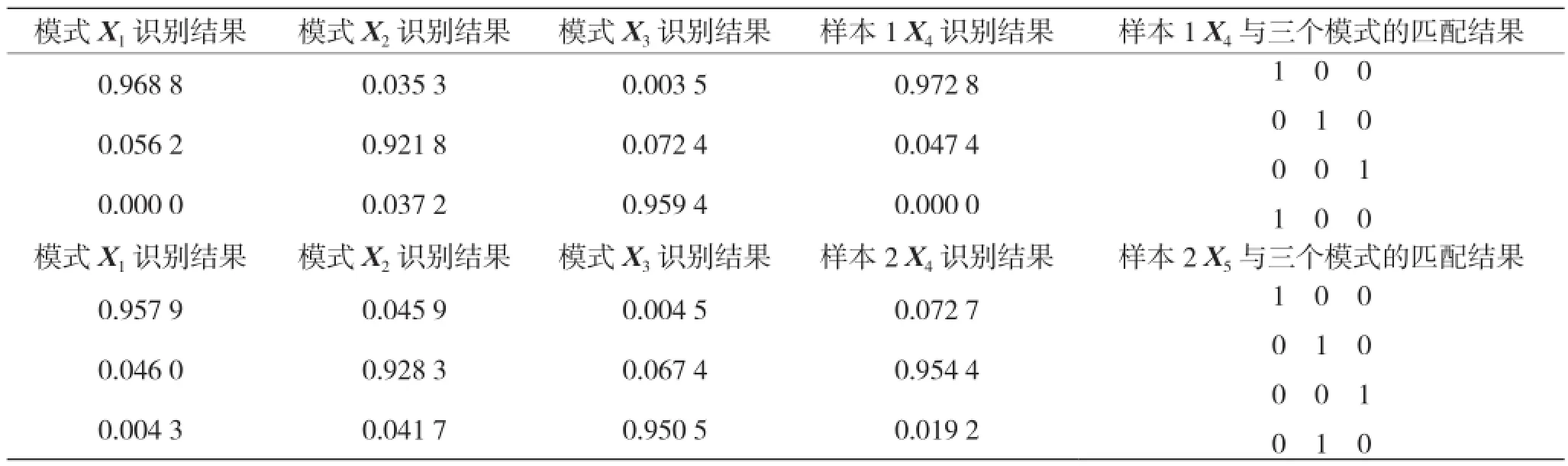
表2　模式识别结果

由表2结果可知，利用矩阵奇异值分解算法联合ESPIRT算法进行无线信道参数提取的参数已经足够精确，可以确保模式正常识别。所以，下面对无线信道参数提取都采用矩阵奇异值分解算法联合ESPIRT算法进行。从表2中的两个样本与三个模式匹配结果的矩阵中可以看到,样本1 X4和模式X1即场景一匹配，样本2 X5和模式2即场景二匹配。因此，模式识别的结果为：样本一的数据属于场景1，样本二的数据属于场景2。

4.3问题三求解

基于微元算法的区域划分实现的微元试探法，建立区域划分模型，设定相关参数，对该条连续路段的真实信道测量结果进行分析，划分路段区域。首先根据基本假设选取“微元”数据，对数据用矩阵奇异值分解算法联合ESPIRT算法进行参数提取。然后用微元试探法进行区域划分，结果如图9所示。

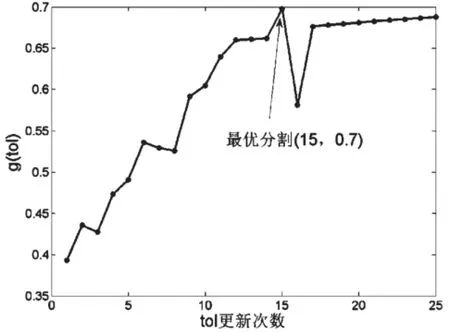
图9　微元试探法结果

由图9可知，最优分割点为（15，0.7）。它所对应的划分结果如表3所示。

表3　区域最优分段结果

4.4问题四求解

对两个真实信道的测量结果利用矩阵奇异值分解算法联合ESPIRT算法进行参数提取，然后用基于BP神经网络算法或微元试探法给出的评判标准进行模式识别。两种算法识别的结果都是：最后的试验数据提供的两个真实信道的结果都属于A9段，即大致120～122 m区段。

5　模型评价

第一，基于存在的问题建立了无线信道参数“指纹”提取算法和“指纹”评价指标模型。对矩阵奇异值分解算法和ESPRIT算法提取的参数进行分析，这两种算法提取的参数能够很好地区别不同的场景。所以实际操作中，只用矩阵奇异值分解算法联合ESPRIT算法提取参数即可。

第二，BP神经元网络算法可以很好地识别场景及样本模式，所以这里采用这种模式识别算法行之有效。

第三，建立的微元试探法能很好地对连续信道区域进行划分，并且模型评价函数也能发挥出很好的评价作用。

［1］ Schmidt R O.Multiple Emitter Location and Signal Parameter Estimation［J］.Antennas and Propagati on，1986，34（03）:276-280.

［2］ LIN T，ZENG X，SUN H.Improved Algorithm for MUSIC Applied in Coherent Signal Parameter Estimation［C］. Electronics and Optoelectronics（ICEOE），2011，2（02）:411-414.

［3］ Roy R，Kailath T.ESPRIT-estimation of Signal Parameters via Rotational Invariance Techniques［J］.Acoustics，Speech and Signal Processing，1989，37（07）:984-995.

［4］ Feder M，Weinstein E.Parameter Estimation of Superimposed Signals Using the EM Algorithm［J］.Acoustics，Speech and Signal Processing，1988，36（04）:477-489.

［5］ Silverman B W，Jones M C，Wilson J D，et al.A Smoothed EM Approach to Indirect Estimation Problems，with Particular Reference to Stereology and Emission Tomography［J］.Journal of the Rotal Statistical Society:Series B（Methodological），1990:271-324.

［6］ Fessler J A，Hero A O.Space-alternating Generalized Expectationmaximization Algorithm［J］.Signal Processing，1994，42（10）: 2664-2677.

［7］ 韩彩.高速铁路场景无线信道参数萃取方法研究［D］.北京:北京交通大学，2015. HAN C.Research on Wireless Channel Parameter Extraction under High-speed Railway Scenario［D］.Beijing: Beijing Jiaotong University，2015.

［8］ 高远.基于SAGE算法的宽带信道参数提取方法的应用研究［D］.南京:南京邮电大学，2012. GAO Y.Parameter Estimation for Broadband ChannelSystem based on SAGE Algorithm［D］.Nanjing:Nanjing University of Posts and Telecommunications，2012.

［9］ 徐树方，钱江.矩阵计算六讲［M］.北京:高等教育出版社，2011. XU Shu-fang，QIAN Jiang.Six Parts of Matrix Calculation［M］.Beijing:Higher education press，2011.

［10］ 杨丹.MATLAB图像处理实例详解［M］.北京:清华大学出版社，2013. YANG Dan.MATLAB Image Processing Examples［M］. Beijing:Tsinghua University press，2013.

王瑞星（1990—），男，硕士，主要研究方向为并行计算、数值并行算法；

刘 斌（1991—），男，硕士，主要研究方向为脉冲功率技术、电磁内爆、电磁场与微波；

杜健鹏（1991—），男，硕士，主要研究方向为图像算法设计与图像处理；

李 明（1990—），男，硕士，助理工程师，通讯作者，主要研究方向为计算机硬件、数据采集。

Recognition of Wireless Channel "Fingerprint" Feature based on Two Algorithms

WANG Rui-xing1， LIU Bin1， DU Jian-peng1， LI Ming2
（1.Graduate School of Chinese Academy of Engineering Physics， Beijing 100088， China；2.Xi'an Aeronautics Computing Technique Research Institute， AVIC， Xi'an Shaanxi 710068， China）

The wireless channel "fingerprint" feature is modelled， which involves the issues like establishment of characteristic parameters of "fingerprint"， matching and recognition， and "region-dividing" of continuous characteristic parameters. The model is solved with the extraction algorithm of wireless channel parameters， BP neural network algorithm， and infinitesimal heuristics proposed by the authors. The numerical results show that based on parameters extracted in different scences by these two wireless channel parameters extraction algorithms including singular-value decomposition of matrix and ESPRIT， the several scenarios could be well distinguished， and meanwhile BP neural network algorithm could also accurately identify the scenes and sample models. Experiment indicates that the infinitesimal heuristics could make enough accurate division of the continuous channel region.

wireless channel； fingerprint； BP neural network； infinitesimal heuristics； feature recognition

TN929.5

A

1002-0802（2016）-10-1271-09

10.3969/j.issn.1002-0802.2016.10.002

2016-06-11；

2016-09-20

data:2016-06-11；Revised data:2016-09-20