二维Hilbert变换研究*
徐晓刚,徐冠雷,王孝通,秦绪佳,王建国,易成涛
(1.海军大连舰艇学院,辽宁 大连 116018;2.浙江工业大学 计算机学院,浙江 杭州 310023)
二维Hilbert变换研究*
徐晓刚1,徐冠雷1,王孝通1,秦绪佳2,王建国1,易成涛1
(1.海军大连舰艇学院,辽宁 大连 116018;2.浙江工业大学 计算机学院,浙江 杭州 310023)
Hilbert变换是信号处理的重要工具之一,具有许多优良性能。对二维Hilbert变换研究工作进行总结,分析传统二维Hilbert变换、分数阶变换域内的二维Hilbert变换、广义分数阶变换域内的二维Hilbert变换等各类二维Hilbert变换的优缺点,同时对与Hilbert变换密切相关的二维Bedrosian定理进行分析,指出现有研究工作中存在的问题和研究方向,以期能为Hilbert变换研究人员提供相关借鉴。
Hilbert变换;Fourier变换;Bedrosian定理;分数阶
0 引 言
受一维Hilbert变换良好性能的鼓舞,人们希望在二维信号(主要指图象)处理上也能获得良好的应用。但研究中发现,二维Hilbert变换并不像想象的那么简单。二维信号的复杂性使一维Hilbert的简单推广并不能取得良好的效果,为此人们进行了多种探索,取得了一些新的成果。
随着研究的深入和新技术的不断涌现,人们希望在各种新领域获得更多类型的变换,以适应不用类型数据的分析、分解要求,使数据分析更加精确、有效。本文根据现有的工作,对Hilbert变换研究状况进行总结,并指出今后研究工作的方向。本文首先简单回顾一维Hilbert变换定义及其特性,然后重点对二维Hilbert变换从不同种类角度出发,综述其概念、特性、构造及其应用等。
1 一维Hilbert变换
一维Hilbert变换的基本定义为:
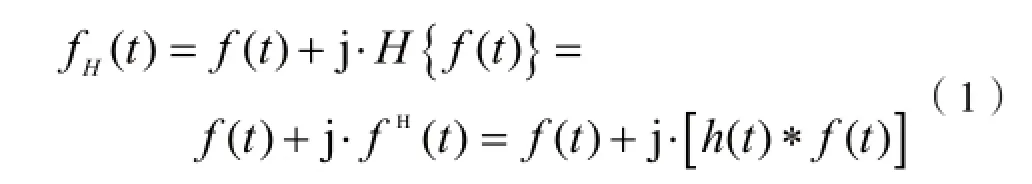
它的频域表达式为:
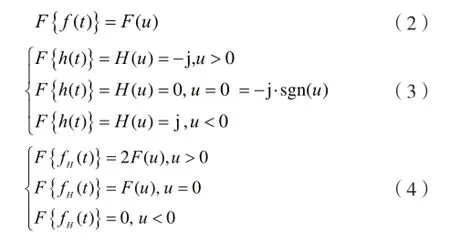
式中,F{ }为Fourier变换算子,sgn( )为符号算子。
Hilbert变换的基本思想:将原实数信号进行Fourier变换得到Fourier频谱,在Fourier频谱中剔除负频率部分,加倍正频率部分幅值,然后对频谱进行Fourier逆变换得到复数信号。在时域内表现为构造复数信号:原实数信号作为实部,把原实数信号和核函数1/πt卷积结果作为虚部。
一维Hilbert变换的优良性质:Hilbert变换前后信号能量不变;把信号进行了π/2相移;二次Hilbert变换后信号反向;四次Hilbert变换后,信号不变。此外,它的优良特性还有时移不变性、缩放不变性、线性性质和卷积特性等。
从上述性质可以看出,Hilbert变换为求解幅度、相位信息提供了简洁、明了的方式,可以充分利用复数域的特殊性质,为后续处理提供一种有效的预处理。因此,在信息通信、信号时频分析、特征识别以及特征提取等方面,Hilbert变换都具有重要的应用价值[1-4]。
2 二维Hilbert变换及多维扩展
受一维Hilbert变换良好性能的鼓舞,人们希望在二维信号(主要指图象)处理上也能获得良好的应用。但研究发现,先后提出的几种二维Hilbert变换都没有达到一维Hilbert变换的良好性能。目前,针对二维信号提出的典型Hilbert变换有:总体Hilbert变换(Total Hilbert Transform,THT)[5],方向Hilbert变换(Partial Hilbert Transform,PHT)[6],单象Hilbert变换(Single Orthant Hilbert Transform,SOHT)[7],四元Hilbert变换(Quaternionic Hilbert Transform,QHT)[8],二象Hilbert变换[9]以及单基解析信号变换[10]。
THT思想比较简单,即将一维信号卷积核进行简单扩展,直接应用于二维信号的卷积处理,起到了“十”字形带限滤波器的作用。一方面它把某些信号进行了±π相移,另一方面THT在频域内保留了关于原点对称的两个象限的能量。因此,THT变换后的信号能量产生了丢失,即丢失了横向和纵向等数据信息。基于这两个主要缺陷,THT不再具有一维Hilbert的各种性质。此外,THT虽然在时域形式上拷贝了一维Hilbert的思想,但是由于二维信号的复杂性,最终导致其在功能和性质上出现了完全背离。目前,THT只作为一种理论探讨的形式出现,实际工程应用并不多见。
PHT更直接,即把一维Hilbert变换在横向和纵向上各做1次。PHT只是一味从形式上借鉴一维Hilbert变换,而没有从一维Hilbert变换的目的和结果的角度进行核函数的构造,从而造成在纵横方向上信息的交错丢失。
SOHT试图克服THT、PHT的不足,仿照一维Hilbert变换的思想进行构造,即对某些信号进行强烈加强,而对其他信号进行抑制。SOHT具有一定的压缩冗余作用,但由于只保留了部分能量,也就丢失了部分信息,无法恢复原数据。
QHT是在SOHT和超Fourier变换(Hypercomplex Fourier transforms,HFT)[11-12]基础上发展出来的。QHT构造的思想和SOHT一致,但其不局限于常规的Fourier变换,而是采用了更为复杂的四元Fourier变换替换常规的Fourier变换。QHT可以获得一些良好性能以弥补SOHT的不足,但是QHT却把信号复杂化了,也不再具有冗余压缩的特性。
与一维Hilbert变换相比,上述四种变换或多或少失去了部分优良特性,包括将信号进行π/2相移的优良特性,且适用范围和应用场合都受到了一定的限制。例如,对于给定的信号,采用上面任何一种变换都会产生无法预知的信息丢失,无法保证将其正确地转换成复数信号。可见,在构造二维Hilbert变换时,上述方法都没有从图象的特点出发,或者只是形式上的模仿,或者只是简单地将图象认为是两类一维信号的叠加,因此不能涵盖图象所有方向上的特征。QHT虽已力图解决这种问题,但通过多次卷积迭加来实现的思路显然不够。图象信息分布于各个方向,单独从时域上看,不便于进行一次性处理。
2007年,徐等从频域角度出发,构造了一种新的二维Hilbert变换——标准二象Hilbert变换[9]。实验证明,这种变换具备了一维Hilbert变换的全部优良性能,包括π/2相移的特性。此外,文献[9]还给出了其他一些非标准二象Hilbert变换。这些变换具有各自独特的性能,如将不同信号分别进行π/2相移和π相移,将不同频率信号进行加倍或者消除等。二象Hilbert变换的特性为图像分析、处理提供了一种有效工具,先后应用于纹理分割、图象增强、边缘提取、图象滤波等方面[9,13-16]。
单基解析信号变换则采用矢量的形式[10],把X、Y方向Hilbert变换进行矢量组合,获得了具有良好特性的矢量Hilbert变换。但是,单基解析信号变换本质上仍然是两个方向上一维Hilbert变换的组合,只不过这种组合方式首次引入矢量概念,可以有效解决某些矢量信号的变换分析。
在获得二象Hilbert变换后,文献[16]给出了多维Hilbert变换的通式。从通式可以看出,一维Hilbert变换和二象Hilbert变换分别是Hilbert变换通式在n=1和n=2情况下的特例。通式的建立为Hilbert变换指明了方向,便于进行理论分析和指导。同时,多维Hilbert变换为实现多维信息的处理提供了一个有效工具。
3 广义变换域的二维Hilbert变换
3.1分数阶变换域内的二维Hilbert变换
分数阶Fourier变换(FRFT)与线性正则变换(LCT)是两种正得到越来越多关注的研究领域。尽管分数阶Fourier变换可以看作线性正则变换的特例,但是人们前期的工作表明,这两种变换具有很多不同的应用背景、特殊场合下的不同物理解释以及不同的某些特性。因此,人们通常会同时对两种变换进行研究,或者是各自独立进行研究。
分数阶Fourier变换是传统Fourier变换的广义形式。传统Fourier变换的物理含义在于把信号从时域转换到频域,从频域的角度观察信号对应成分在相应频率上的“含量”。在时频平面上,传统Fourier变换把时域内信号旋转90°到达频域;而分数阶Fourier变换可以把时域内信号在时频平面上旋转任意角度,到达时域和频域间的任意域内,实现一种“参数化”的控制功能。
文献[17-22]从多种角度对一维Hilbert变换在FRFT域的性能进行描述。从研究工作可以看出,在FRFT域,一维Hilbert变换呈现出更多的表示形式,也具备更多的性能特征。特别是其相移特性,在信号分析中体现了更强大的精细控制功能。
对于FRFT域的二维Hilbert变换,根据能量分布的不同形式,文献[23]给出了几种典型的变换:方向Hilbert变换、全向Hilbert变换、单象Hilbert变换等。研究工作表明,FRFT域的二维Hilbert变换具有多种新的特性,且与分数阶的参数相关。
这些特性包括:
(1)方向Hilbert变换与传统Hilbert变换的物理意义一致,但这种对应关系受到分数阶数α和β的影响。
(2)全向Hilbert变换的解析信号对应于分数阶Fourier变换域内的线性组合,为信号在分数阶Fourier变换域实现全向Hilbert变换提供了捷径。
(3)方向Hilbert变换和全向Hilbert变换之间存在函数变换的等价关系。
(4)分数阶Fourier域的单象解析信号是方向Hilbert变换信号和全向Hilbert变换信号的线性组合。
(5)所有的广义Hilbert变换都可以在分数阶Fourier变换域内直接实现,该结论为分数阶Hilbert变换的快速实现创造了理论条件。
(6)FRFT域,常数的Hilbert变换不为零,而是与分数阶数(α, β)相关的线性调频函数。
3.2广义分数阶变换域内的二维Hilbert变换
线性正则变换(Linear Canonical Transform,LCT)又称广义分数阶Fourier变换,是分数阶Fourier变换和Fresnel变换等的广义形式[3-4,15,17]。与分数阶Fourier变换相比,线性完整变换的参数多,其具有与参数相关的一些特性。
LCT域的Hilbert变换研究工作相对较少。文献[24]给出了LCT域的几种二维Hilbert变换,包括方向Hilbert变换、全向Hilbert变换、单象Hilbert变换,同时给出了各自的性能分析。在LCT域,二维Hilbert变换具有许多传统时域的类似性能特征,包括时频域对应关系、卷积特性等,但这些性能都受到变换参数的影响。
具体的,一些特性如下:
(1)LCT域的方向Hilbert变换广义解析信号在LCT域内将负信号部分置零,而正信号部分加倍,与传统Hilbert变换的物理意义相对应,但这种对应关系受到变换参数的影响。
(2)全向Hilbert变换与方向Hilbert变换沿着X、Y方向变换后的结果相同。
(3)对于任意二维实信号f(x,y)(x, y∈R),其LCT域的单象广义解析信号是方向广义Hilbert变换信号和全向广义Hilbert变换信号的线性组合。
(4)LCT域的Hilbert变换可在LCT域内直接实现。该结论为LCT域Hilbert变换的快速实现创造了理论条件,即在变换域内直接实现后再逆变换。
(5)LCT域Hilbert变换为零的函数不是常数,而是与变换参数相关的线性调频函数。
4 二维Bedrosian定理
Bedrosian定理是信号处理领域的一个基础性工作,也是数学领域的一个基本工作。它来源于Hilbert变换,是Hilbert变换的重要特性之一,但又可独立于Hilbert变换[25-28]。Bedrosian定理规定:对于两个实数信号相乘的形式进行Hilbert变换后,只有满足一定频率条件的信号变成了复数,而另一信号没有任何变化。目前,一维Bedrosian定理相对成熟,但是二维Bedrosian定理存在不少空白。
早在2008年,Venouziou等人首次给出了多维Bedrosian定理(包含二维)的一个数学表达式[25](即方向Hilbert变换对应的Bedrosian定理,简称方向Bedrosian定理)。它通过对多维空间进行一维Bedrosian定理(在每一维空间中均作为一个一维信号处理)的多次组合,获得多维Bedrosian定理的理论条件和表达形式。Venouziou等认为,要获得多维信号类似于一维函数那样的Bedrosian定理,可以通过分析不同维空间的一维Bedrosian定理进行讨论,把一维Bedrosian定理的理论条件在二维和多维空间内进行支撑范围的并集和交集运算。但是,Venouziou等人的方向Bedrosian定理并不是从信号处理的角度进行探讨,也没有考虑多维信号(例如,二维图像)的特性(包括纹理结构特性、统计特性、自然特性等),因此对于方向相关的信号适应性较差,且其纯粹是从数学角度对一维Bedrosian定理在二维和多维空间上直接扩展。
2011年,文献[23]从频域的角度分析和理解复数信号,并对方向Bedrosian定理进行了深入分析,将其扩展到广义分数阶域,并给出了详细的参数讨论,从而从信号处理角度(分数阶Fourier变换)对二维Bedrosian定理开展分析研究。同时,该文献还讨论了交叉象Hilbert变换的Bedrosian定理(简称交叉象Bedrosian定理),给出了详细的应用参数、理论条件和表达形式。但是,该研究理论只适合于广义域内方向不相关的二维信号,并不适合其他类型的信号,且并未详细论证其在图像中的具体应用。
为了获得二维Bedrosian定理在信号处理中的应用,2012年文献[26]从二维图像信号单分量和多分量定义的角度,使用了二象Hilbert变换对应的Bedrosian定理(简称二象Bedrosian定理)。这是二维Bedrosian定理对图像进行应用的具体实例。通过二象Bedrosian定理界定了二维单分量和多分量的定义,为后续图像的分量分解提供了理论支撑。但遗憾的是,该工作只是应用了二象Bedrosian定理给出的概念,并没有给出二象Bedrosian定理具体的理论条件,也没有给出二象Bedrosian定理相应的理论证明。
2014年,Zhang等人[27]又在Venouziou等人工作[25]的基础上,进一步对多维(包括二维)方向Bedrosian定理进行探讨,优化Venouziou等人提出的多维方向Bedrosian定理的理论条件,给出了更进一步的理论证明和分析,并将Bedrosian定理从实数和实数相乘扩展到实数和复数相乘、复数和复数相乘等更复杂的形式。同时,利用Bedrosian定理等式关系构造时频分析基函数,为多维信号的理论分析和应用提供了理论依据。但是,Zhang与Venouziou等人工作一样,其理论对于具有方向相关性的信号适应性较差,且不是从信号处理角度出发,而是纯粹从数学理论条件上加以分析,也没有给出在信号处理方面的具体应用。
综上所述,到目前为止,也只有方向Hilbert变换及交叉象Hilbert变换有对应的二维Bedrosian定理,其余几种二维Hilbert变换对应的二维Bedrosian定理基本空白。此外,方向Hilbert变换及交叉象Hilbert变换有对应的二维Bedrosian定理也只是一维Bedrosian定理在二维空间的直接扩展,没有充分考虑图像结构特性[29-31],尽管其分辨率分析可以有效提高[32]。
5 发展方向
经过多年的努力,对Hilbert变换的研究已经取得了一些新成果,为后续的各种应用和分析打下了良好基础。但是,从Hilbert变换的已有工作可以看出,在一些新领域还没有相应的变换方法。因此,如何在工程上实现良好的应用还需要进行大量的工作。
值得进一步研究的工作包括以下方面:
第一,构造快速的算法。构造快速的算法,实现实时计算,应用于多种时间限制的场合。Hilbert变换的基础是Fourier变换,分数阶Hilbert变换的基础是分数阶Fourier变换。Hilbert变换与Fourier变换的耗时量息息相关。快速Fourier变换虽然可以大幅度缩短计算时间,但还无法满足各种应用的快速计算需求。
第二,研究多维分数阶Hilbert变换的构造方法。现有的研究工作表明,在多维信号领域,信号呈现了更多的特征,需要更多的表述参量。与此相对应,多维Hilbert变换具有更多的表现形式,体现出了不同的性能特征。在多维分数阶Hilbert变换方面,根据分数阶Fourier变换的强大信号分离能力,可以预测多维分数阶Hilbert变换也可以获得更精细的分解优势:可以通过控制角度、相位等信息,实现精确的定向变换,把图象特定方向的信息进行提取和增强,以提取特定频域的层次信息,通过增强或滤波等处理,获得目标的有效处理结果。多维分数阶Hilbert变换的“参数化”精细控制功能,将在图象图形的处理上发挥重要作用。由于多维分数阶Fourier变换还有许多问题没有解决,因此相应的Hilbert变换还有待于深入研究。
第三,研究其他域Hilbert变换的构造方法。除了已有的分数阶Fourier变换和LCT变换,还有许多有效的变换方法。对这些变换域进行研究,以期获得更多具有优良特性的Hilbert变换。
第四,研究一些特殊性能的Hilbert变换。以往的研究发现,在多维信号的Hilbert变换方面,还存在许多次优的变换。这些变换可能只具备一维Hilbert变换中的部分优越特性,但具有一些新的特性,如已发现其中一种变换可以实现π/4相移。另外,结合频带、方向等限制,可以构造更多具有某种特性的变换,以应用于多种特殊的领域。
第五,研究二维Bedrosian定理。人们已经意识到[3,5-6],在一维信号中,Bedrosian定理虽然是Hilbert变换的一个特性,但却是Hilbert变换的核心。这表明:对两个(或多个)实数信号相乘的形式进行Hilbert变换后,其中只有满足一定条件的信号变成了复数或发生了相移,而其他信号保持不变,即Bedrosian定理决定了Hilbert变换的结果形式。由于一维信号自由度少、相对简单,因而以往人们这样使用并没有造成不便。但是,对于二维信号,正如Jonathan和Sofia在其工作中论述的那样[33],维数的增加往往意味着一定概念和思想的突破。图像相对于一维信号增加了一个自由度后,既要考虑图像的自身结构特征和类型,又要考虑二维Hilbert变换的种类,同时还要考虑应用的目的(即需求和目标是什么),因此其研究具有很大的挑战性。
第六,对其他变换的启发。Hilbert变换只是众多变换的一种。通过研究Hilbert变换的相关工作,可以为其他变换的研究提供一种新的思路。
综上可见,一维Hilbert变换在信号分析与处理上已经获得广泛的应用,可以预见,在各种域内,具备更多优良性能的多维Hilbert变换,必将在图象、视频、3D网格、动画等多维信号的分析和处理方面发挥重要的作用。
6 结 语
本文对二维Hilbert变换研究状况进行了总结。与传统Hilbert变换相比,二维Hilbert变换有着更加复杂的形式和性能。针对不同类型约束,需要建立不同的变换形式,适用于不同状态下的信号处理。随着各领域研究的深入,这种需求也会越来越多地引起人们的关注。
[1] Gabor D.Theory of Communication[J].Proceedings of the Institute of Electrical Engineers,1946,93(26):429-457
[2] Ville J.Theorie et Applications de la Notion de Signal Analytique[J].Cables et Transmission,1948,(2A):61-74.
[3] Boashash B.Estimating and Interpreting the Instantaneous Frequency of a Signal-Part 1:Fundamentals[J].IEEE Proc,1992,80(04):520-539.
[4] Boashash B.Estimating and Interpreting the Instantaneous Frequency of a Signal-Part 2:Algorithms and Applications[J].IEEE Proc,1992,80(04):540-568.
[5] Stark H.An Extension of the Hilbert Transform Product Theorm[J].IEEE Proc,1971,59(09):1359-1360.
[6] Havlicek J P,Havlicek J W,Mamuya N D,et al.Skewed 2D Hilbert Transforms and Computed AM-FM Models[C]. IEEE International Conference on Image Processing,1998,(59):602-606.
[7] Stefan L,Hahn.Multidimensional Complex Signals with Singleorthant Spectra[J].IEEE Proc,1992,80(08):1287-1300
[8] Thomas B,Gerald S.Hypercomplex Signals-a Novel Extension of the Analytic Aignal to the Multidimensional Case[J].IEEE Transaction on Signal Processing,2001,49(11):2844-2852.
[9] XU Guan-lei,WANG Xiao-tong,XU Xiao-gang.Biorthant Hilbert Transform[J].Progress in Natural Science,2007,17(08):1120-1129.
[10] Felsberg M,Sommer G.The Monogenic Signal[J].IEEE Transactions on Signal Processing,2001,49(12):3136-3144.
[11] Chang J H, Pei S C,Ding J J.2D Quaternion Fourier Spectral Analysis and Its Applications[J].IEEE Proceedings of the International Symposium on Circuits andSystems,2004,(03):241-244.
[12] Sangwine S J,Ell T A.Hypercomplex Fourier Transforms of Color Images[M].Los Alamitos CA:IEEE Computer Society Press,2001:137-140.
[13] XU Guan-lei,WANG Xiao-tong,XU Xiao-gang.Improved bi-dimensional EMD and Hilbert Spectrum for the Analysis of Textures[J].Elsevier Pattern Recognition,2009,42(05):718-734.
[14] XU Guan-lei,WANG Xiao-tong,XU Xiao-gang.The Logarithmic,Heisenberg’s and Windowed Uncertainty Principles in Fractional Fourier Transform Domains[J]. Elsevier Signal Processing,2009,89(03):339-343.
[15] XU Guan-lei,WANG Xiao-tong,XU Xiao-gang.Fractional Quaternion Fourier Transform, Convolution and Correlation[J].Elsevier Signal Processing,2008,88(10):2511-2517.
[16] XU Guan-lei,WANG Xiao-tong,XU Xiao-gang.Extended Hilbert Transform for Multidimensional Signals[J].IEE/ IET proc.,2008,(01):292-297.
[17] Zayed A I.Hilbert Transform Associated with the Fractional Fourier Transform[J].IEEE Signal Processing Letters,1998,5(08):206-208.
[18] Fu Y X,Li L Q.A Generalized Bedrosian Theorem in Fractional Fourier Domain[J].IEEE Proc,2006:1785-1788.
[19] Lohmann A W,Mendlovic D,Zalevsky Z.Fractional Hilbert Transform[J].Opt Lett,1996,21(04):281-283.
[20] Pei S C,Yeh M H.Discrete Fractional Hilbert Transform[J]. IEEE Trans Circuits and Systems-II:Analog and Digital Signal Processing,2000,4(11):1307-1311.
[21] Tseng C C,Pei S C.Design of Discrete-time Fractional Hilbert Transformer[J].IEEE Proc,ISCAS,2000,(05):525-528.
[22] Pei S C,Ding J J.The Generalized Hilbert Transform and Its Applications to 2-D Edge Detection[J].IEEE Proc,ICASSP,2003,III:357-360.
[23] 徐冠雷,王孝通,徐晓刚.分数阶Fourier域的二维广义Hilbert变换及Bedrosian定理[J].数学物理学报,2011,31(03),814-828. XU Guan-lei,WANG Xiao-tong,XU Xiao-gang.2D Hilbert Transform and Bedrosian’s Principle Associated with Fractional Fourier Transform[J].Acta Mathematica Scientia,2011,31(03):814-828.
[24] XU Guan-lei,WANG Xiao-tong,XU Xiao-gang.Generalized Hilbert Transform and Its Properties in 2D LCT Domain[J]. Signal Processing,2009,(89):1395-1402.
[25] Venouziou M,Zhang H.Characterizing the Hilbert Transform by the Bedrosian Theorem[J].Journal of Mathematical Analysis & Applications,2008,338(02):1477-1481.
[26] Xu G,Wang X,Xu X.On Analysis of Bi-dimensional Component Decomposition via BEMD[J].Pattern Recogni tion,2012,45(04):1617-1626.
[27] Zhang H.Multidimensional Analytic Signals and the Bedrosian Identity[J].Integral Equations & Operator Theory,2014,78(03):301-321.
[28] Cerejeiras P,Chen Q,Kaehler U.Bedrosian Identity in Blaschke Product Case[J].Complex Analysis & Operator Theory,2012,6(01):275-300.
[29] Guanlei X,Xiaotong W,Lijia Z,et al.Time-Varying Bandpass Filter based on Assisted Signals for AMFM Signal Separation:A Revisit[J].Journal of Signal and Information Processing,2013,(04):229-242.
[30] Guanlei X,Xiaotong W,Xiaogang X,et al.The Bi-Dimensional Bedrosian’s Principle for Image Decomposition[J]. Applied Mechanics and Materials,2014,(602-605): 3854-3858.
[31] Guanlei X,Xiaotong W,Xiaogang X,et al.Amplitude and Phase Analysis based on Signed Demodulation for AM-FM Signals[J].Journal of Computer and Communications,2014,(02):87-92.
[32] Guanlei X,Xiaotong W,Xiaogang X.Generalized Uncertainty Principles Associated with Hilbert Transform[J].Signal Image and Video Processing,2014,8(02):279-285.
[33] Jonathan M,Lilly,Sofia C.Olhede,Bivariate Instantaneous Frequency and Bandwidth[J].Signal Processing,2009,58(02):591-603

徐晓刚(1967—),男,博士,教授,主要研究方向为虚拟现实;
徐冠雷(1978—),男,博士,讲师,主要研究方向为信号处理;
王孝通(1962—),男,博士,教授,主要研究方向为信号处理;
秦绪佳(1968—),男,博士,教授,主要研究方向为图象处理、可视化;
王建国(1981—),男,博士,讲师,主要研究方向为图象处理、虚拟仿真;
易成涛(1974—),男,博士,副教授,主要研究方向为图象处理、航海技术。
Review of Bidimensional Hilbert Transform
XU Xiao-gang1, XU Guan-lei1, WANG Xiao-tong1, QIN Xu-jia2, WANG Jian-guo1, YI Cheng-tao1
(1.Dalian Naval Academy, Dalian Liaoning 116018, China;2.College of Computer Science &Technology, Zhejiang University of Technology, Hangzhou Zhejiang 310023, China)
Hilbert transform is one of the useful tool in signal processing, and much effective performance have been found. In this paper, the current work of the bi-dimensional Hilbert transform is reviewed,the advantage and shortage of different kind of bi-dimensional Hilbert transform is analyzed, they are the traditional bi-dimensional Hilbert transform, bi-dimensional Hilbert transform in fractional Fourier transform domains, bi-dimensional Hilbert transform in generalized fractional Fourier transform domains,by the way, bi-Dimensional Bedrosian’s Principle is analyzed too. At last, current questions and some useful further study work are proposed, in order to provide the relevant reference for the Hilbert transformation researchers.
hilbert transform; fourier transform; bedrosian theorem; fractiona
National Natural Science Foundation of China(No.60975016,No.61002052,No.61471412,No.61273262);Natural Science Foundation of Liaoning Province(No.2015020086)
TN911.7
A
1002-0802(2016)-10-1265-06
10.3969/j.issn.1002-0802.2016.10.001
2016-06-11;
2016-09-08
data:2016-06-11;Revised data:2016-09-08
国家自然科学基金项目(No.60975016,No.61002052,No.61471412,No.61273262);辽宁省自然科学基金项目(No.2015020086)
——信号处理

