高速铁路隧道沉降变形分析方法的研究

彭仪普，张盼，薛一奇

(中南大学 土木工程学院，湖南 长沙 410075)



高速铁路隧道沉降变形分析方法的研究

彭仪普，张盼，薛一奇

(中南大学 土木工程学院，湖南 长沙 410075)

以长株潭城际铁路线下工程沉降变形观测评估项目为依托，研究长株潭城际铁路隧道沉降的发生发展规律，通过现场实测数据，发现隧道沉降量普遍偏小，分别用双曲线拟合法和灰色预测模型对同一组长株潭综合II标树木岭隧道的沉降数据进行拟合，并分析实测和预测沉降的差异，并比较2种模型的适用性。研究结果表明：双曲线沉降的模拟需要大量的样本，可以作为隧道沉降评估的一种方法，但是仅对少数累积沉降递增的情况模拟精度高；灰色预测所需样本小，运算简便，而且模拟精度高，因此，灰色预测相比双曲线拟合法具有更高的精度和普适性。

双曲线；灰色预测；隧道；沉降分析

由于无砟轨道对高度的可调节性很小，要求无砟轨道铺设前基础沉降必须在一个很小的范围内，本文根据长株潭城际铁路综合Ⅱ标线下工程沉降变形评估自评报告及沉降变形过程数据电子文件，选取路段为由中铁十四局承建的长株潭城际铁路树木岭隧道进树区间～树木岭车站北段YDK1+439.736～YDK4+372.356区段，总长度为2 932.62 m，其中YDK1+795.417～YDK4+025.000为盾构段，针对该盾构段的沉降数据特点进行双曲线法和灰色预测法的模拟分析，着重研究分析双曲线法和灰色预测对于隧道沉降评估的适用性及精度。

1　隧道沉降的机理分析

长株潭城际铁路线下工程隧道段均采用盾构施工，在盾构机顶进过程中很难避免临近的土体被扰动，因此产生地层损失及沉降，因盾构法施工形成沉降的2个主要因素为地层损失和经扰动后的土颗粒再次固结。

地层损失一般情况下可以分为3种：第1种为正常的地层损失，除却主观因素，姑且认为操作的过程是仔细认真的，符合规定的操作规程。在这种假设下，地层损失即可全部由施工现场的客观条件造成，比如施工场地的地形地质条件以及盾构施工工艺的选择等。第2种为非正常地层损失，这种损失由在盾构施工的过程中因操作失误引起。比如盾构过程中的设置参数错误、压浆不及时以及超挖等问题。第3种为灾害性的地层损失。某些特殊情况下，盾构施工过程中遇到地层中有量比较大的贮水或者遇到水压大而且透水性强的颗粒状土的透镜体，盾构开挖面会有突发性流动，严重的会形成暴发性崩塌，引起灾害性的地面沉降。由于地层损失致使隧道内埋设的观测标的沉降累积减少，或者由于埋设观测标的滞后，沉降损失已经在盾构过程中损失，这也是造成隧道沉降普遍偏小的主要原因。

固结沉降可分为主固结沉降和次固结沉降。由于隧道一般均处在含水岩层中，盾构推进过程中，挤压、超挖和盾尾的压浆作用会对地层产生扰动，并使周围地层产生正负超孔隙水压力，压力差的产生使开挖排水后容易造成地下水不断渗出，形成多个渗水通道，使地层持续失水，进而导致土层空隙和节理裂隙固结收缩，引起地层沉降。由此可以看出，超孔隙水压力在消散的过程中造成土层压密。

2　双曲线对于隧道沉降评估的适用性

2.1双曲线的理论基础

(1)

(2)

其中：St为时间t时的沉降量；S0为初始沉降量，且S0=0；a和b为荷载不变后经实测数据回归求得的系数。双曲线法是假定下沉平均速率以双曲线形式减少的经验推导法，要求恒载开始后的沉降实测时间至少观测6个月以上。

2.2双曲线应用实例

表1为从几百条记录中选取的8个观测标数据。

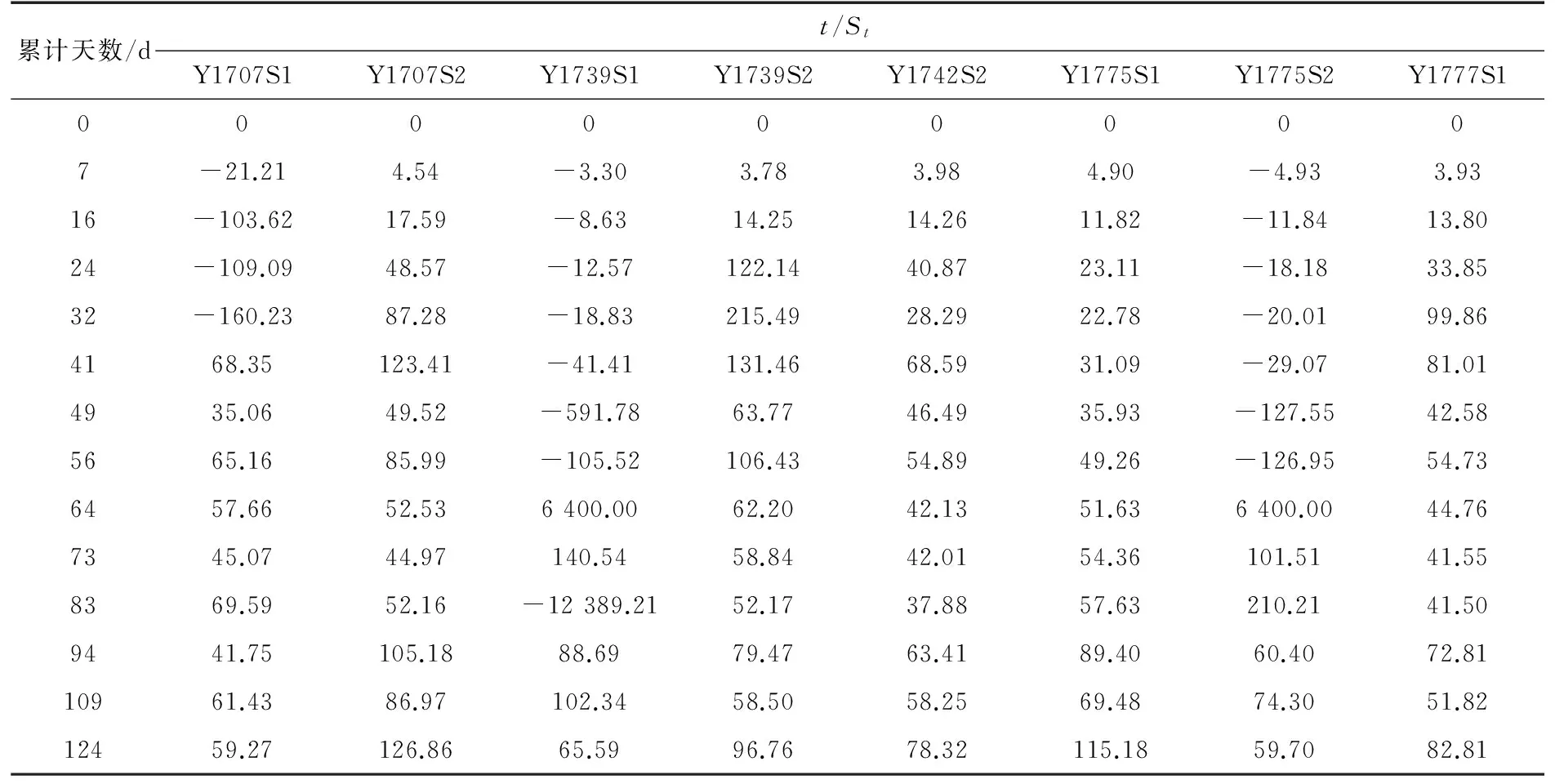
表1　树木岭隧道观测标t/St数据Table 1 Data of the t/St for Shumuling tunnel

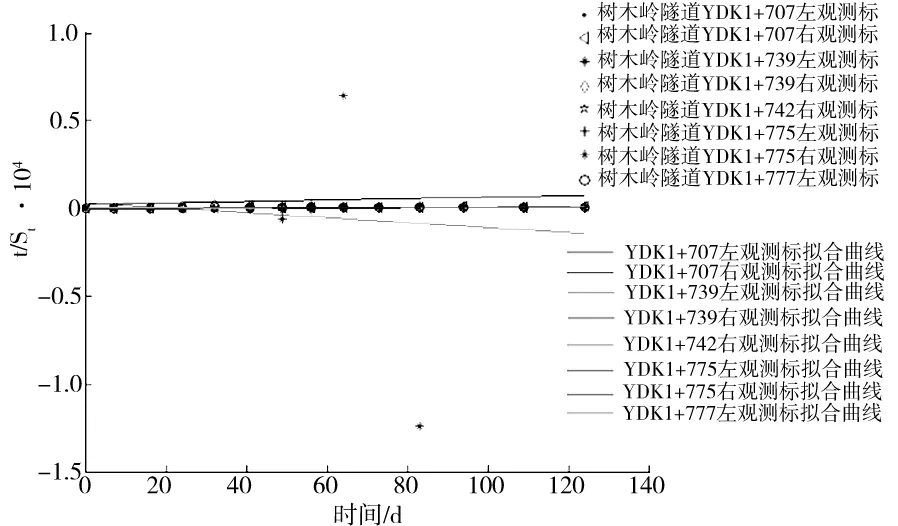
图1　t/St与t的关系Fig.1 Graph of the relationship between the t/St and the t

从图1可以看出，St与t呈线性关系，它们满足式(1)，因为S0=0，这样St与t的关系式为：

(3)

但是由于隧道的沉降量比较小，由于误差的存在，t/St的误差增大，选取具有普遍特征性的树木岭隧道YDK2+200左观测标观测数据如表2。

从图2可以看出，双曲线模拟得到的R2=0.056 3<0.95，双曲线模拟精度非常低。在表2的前3次测量中，总沉降不是像理论情况那样是递增的，即观测点的高程先变大而后逐渐减小，这是由多方面因素造成的，不仅存在测量误差，它包括仪器误差、人员误差、环境误差，还包括盾构施工方法

所造成的误差，通常一定的地基变形伴随盾构的推进过程，其原因可以归为以下几个方面：

1)因为开挖面上的土水压力不平衡而导致开挖面失稳。当压力舱的压力大于开挖面土压力和水压力时会出现地基隆起，而当压力舱的压力小于开挖面土压力和水压力时会出现地基沉降。

在盾构推进过程中会对周围的岩土造成扰动。主要表现在盾构机的板壳和周围岩土的摩擦和扰动，尤其是在曲线推进、蛇曲修正时如果采用超挖会引起地基的隆起和沉降，影响的围岩范围变大，同时也使地基的沉降量变大。

2)在盾构推进过程中会对周围的岩土造成扰动。主要表现在盾构机的板壳和周围岩土的摩擦

图2　树木岭隧道YDK2+200左观测标双曲线模拟Fig.2 Graph of the left observation point YDK2+200 for Shumuling tunnel

次数日期累计天数/d相邻两次观测时间间隔/d高程/m本次沉降/mm总沉降/mm12015-01-070016.452720.000.0022015-01-147716.454121.401.4032015-01-2316916.45343-0.690.7142015-01-3124816.45301-0.420.2952015-02-0832816.45249-0.52-0.2362015-02-1741916.45180-0.69-0.9272015-02-2549816.45092-0.87-1.8082015-03-0456716.451250.33-1.4792015-03-1264816.45069-0.56-2.03102015-03-2173916.44999-0.70-2.73112015-03-3082916.450290.31-2.43122015-04-0891916.44909-1.20-3.63132015-04-17100916.44875-0.34-3.97142015-04-26109916.448900.15-3.82152015-05-03116716.44854-0.36-4.18162015-05-11124816.44828-0.26-4.44

和扰动，尤其是在曲线推进、蛇曲修正时如果采用超挖会引起地基的隆起和沉降，影响的围岩范围变大，同时也使地基的沉降量变大。

3)盾尾空隙的发生和壁后注浆的不足也会引起沉降。只要存在盾构施工，就必然存在盾尾空隙， 这种空隙会引起地基的应力释放同时产生弹塑性变形。可以通过壁后注浆来控制，但是壁后注浆的注浆量、材料、位置、时间、压力等都会对地基的变形造成影响。

4)地下水位下降。由于渗漏水或降水会引起地基沉降。

5)衬砌管片的变形及变位。管片从盾尾脱出后会受到围岩荷载的作用而发生变形或者变位，造成地基沉降，但其量较小可忽略不计。

由于地层损失是致使隧道内埋设的观测标的沉降累积减少的主要原因，这就使由于其他方面的误差比如埋设观测标的滞后以及人员误差的比例放大，因此双曲线法的精度大打折扣。

选择累积沉降递增的一组湘江隧道WDK7+945左观测标观测数据如表3。

表3　湘江隧道WDK7+945左观测标观测数据Table 3 Data of the left observation point WDK7+945 for Xiangjiang tunnel

图3　湘江隧道WDK7+945左观测标双曲线模拟图Fig.3 Graph of the left observation point WDK7+945 for Xiangjiang tunnel

从图3可以看出，当累积沉降递增时，双曲线模拟的R2=0.970 9>0.95，这表明模拟精度高，模拟情况良好，并且可以得到t与St的线性关系:t/St=5.922 4+0.244 7 t,Sf=S0+1/b=1/0.244=4.09 mm，Sf为最终沉降量。在实际情况中，像这样累计沉降递增的理想情况不多见，所以，双曲线法对于沉降量较小且普遍存在误差的隧道观测标沉降量的模拟精度不高。

3　灰色预测模型的理论及精度检测

灰色预测所研究的系统往往含有不确定性因素。但是这些不确定因素不是杂乱无章的，他们存在某种关联，且可利用已知信息对这种关联发展的趋势进行相关性分析，通过处理后的具有比较明显规律的数据预测事物发展趋势。然后建立相应的微分方程。利用系列具有等时距的数据构建灰色预测模型，利用模型可以预测未来某个时刻的特征量，以及达到某一特征量所需要的时间。

灰色预测总体思想是将随时间变化的随机正的数据列累加，得到非负递增数据列，用适当的方式逼近，以次曲线作为预测模型来预测。如本文所使用的GM(1,1)采用单一变量，需要的时间序列数据是平缓变化的。

3.1灰色GM(1,1)模型的建立方法

(4)

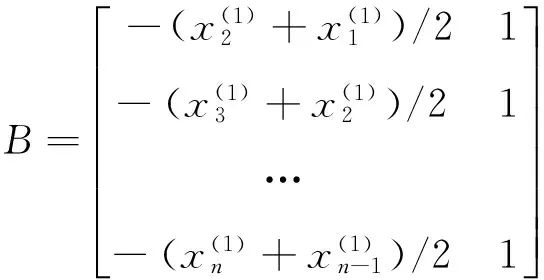
(5)

(6)

以上就是GM(1，1)模型建立的一般过程。用微分法建立单一变量一阶常系数的微分方程，数据环境并没有改变，且是普适性较高的系统。

3.2灰色预测的精度检验

3.3灰色GM(1,1) 模型建立

此处依然采用表2树木岭隧道YDK2+200左观测标观测数据，因为此数据更具有普遍性，利用 MATLAB 编程语言建立 GM(1，1)预测模型，灰色预测的代码如下：

>> x=xlsread('灰色预测.xls');

>> n=length(x);

>> xx=ones(n,1);

>> xx(1)=x(1);

>> for i=2:n;

xx(i)=xx(i-1)+x(i);

end

>> B=ones(n-1,2);

>> for i=1:(n-1)

B(i,1)=-(xx(i)+xx(i+1))/2;

B(i,2)=1;

end

>> BT=B';

>> for j=1:(n-1);

XN(j)=x(j+1);

end

>> XN=XN';

>> A=inv(BT*B)*BT*XN;

>> a=A(1);

>> u=A(2);

>> t=u/a

t =6.515 4e+005

>> i=1:(n-1);

>> xxs(i+1)=(x(1)-t).*exp(-a.*i)+t;

>> xxs(1)=x(1);

>> for j=n:-1:2

>>xs(j)=xxs(j)-xxs(j-1);

>> xs(1)=x(1);

end

>> xs=xs'

>> i=1:n;

>>e(i)=x(i)-xs(i);

>> e=e'

>> sa=mean(x);

>> i=1:n;

>> c(i)=(x(i)-sa).^2

>> sb=mean(c)

sb =3.345 4e-006

>> g=mean(e);

>> i=1:n;

>> h(i)=(e(i)-g).^2;

>> q=mean(h);

>> w=sqrt(q/sb);

w =0.174 7

>> i=1:n;

>> o(i)=e(i)-g;

>> r=max(abs(o))

r =6.7846 e-004

原数据序列与灰色预测模拟数列对比如表4。

由表4可以看出，残差中绝对值最大的为0.68 mm,表明灰色预测模型能够较好地拟合沉降量较小且普遍存在误差的隧道观测标沉降量，时间序列数据是平缓变化的，最大的时间差距为9 d，最小的为7 d。

4　结论

1)双曲线沉降的模拟需要大量的样本，对于观测次数少且存在误差的情况就会使模拟精度降低，虽然可以作为隧道沉降评估的一种方法，但是仅对少数累积沉降递增的情况模拟精度高。

表4树木岭隧道YDK2+200左观测标原始数据与模型改良数据对比

Table 4 Data comparison between the originality and the simulated data of the left observation point YDK2+200 for Shumuling tunnel

次数实测高程/m灰色预测模型高程/m残差/mm116.4527216.452720.00216.4541216.453680.44316.4534316.453260.17416.4530116.452850.16516.4524916.452430.06616.4518016.45202-0.22716.4509216.45160-0.68816.4512516.451190.07916.4506916.45077-0.081016.4499916.45035-0.371116.4502916.449940.351216.4490916.44952-0.431316.4487516.44911-0.361416.4489016.448690.211516.4485416.448280.261616.4482816.447860.42

2)灰色预测可以根据少量且不完全的数据信息建立模型同时做出预测，它是一种综合运用数学方法对不完全的信息进行预测的理论和方法。其思路是首先将与时间有关的已知信息按照某种规则组合, 构成白色模块, 然后按某种规则提高灰色模块的白化度,所以可以应用有限的信息建模，由于灰色预测所需样本小，运算简便，而且模拟精度高，因此在沉降评估中可以得到广泛的应用。

[1]尚金光,张献州,官超伟.高速铁路沉降评估中工程沉降和区域沉降的可区分性研究[J].测绘科学,2013,38(1):84-86.

SHANG Jinguang,ZHANG Xianzhou,GUAN Chaowei. Distinguishability of engineering settlement and land subsidence in the settlement evaluation of high-speed railway[J]. Science of Surveying and Mapping,2013,38(1):84-86.

[2]刘生容,黄文华,游振兴,等.京沪高速铁路沉降趋势分析与预报方法的研究[J].测绘信息与工程，2012,37(1)：24-25.

LIU Shengrong,HUANG Wenhua,YOU Zhenxing, et al. Beijing-Shanghai high-speed railroad subsidence trend analysis and forecast method [J]. Journa1 of Geomatics, 2012, 37(1):24-25.

[3]明祖涛,刘军,夏力,等.改进的灰色模型在高铁沉降预测中的应用[J].测绘科学,2015,40(4):137-140.

MING Zutao,LIU Jun,XIA Li,et al.Study of the implemetion of improved grey model in high-speed railway settlement prediction[J]. Science of Surveying and Mapping, 2015,40(4):137-140.

[4]许双安,任晓春,袁永信.高速铁路沉降数据处理与评估系统设计与实现[J].测绘地理信息,2014,39(4):54-57.

XU Shuangan,REN Xiaochun,YUAN Yongxin. Design and realization of data processing and evaluation system for foundation settlements of high [J]. Journal of Geomatics,2014,39(4):54-57.

[5]虞先溢.高速铁路路基沉降变形分析方法与评估实践[D].成都:西南交通大学,2011.

YU Xianyi. Settlement analysis and assessment practice in high speed railway [D].Chengdu: Southwest Jiaotong Univercity,2011.

[6]罗存喜.Asaoka法在高速铁路沉降分析中的应用[J].土 工 基 础,2013,27(2):79-82.

LUO Cunxi. Application of asaoka method in predicting the settlement of high-Speed rail embankments[J].Soil Engineering and Foundation, 2013,27(2):79-82.

[7]陈超,张献州,尚金光.高速铁路沉降观测数据生产过程质量控制与管理[J].高速铁路技术,2011,2(5):25-29.

CHEN Chao,ZHANG Xianzhou,SHANG Jinguang.Q-uality control and management in data production process of high-speed railway settlement observation[J]. High Speed Railway Technology, 2011,2(5):25-29.

[8]Yamaguchi I,Yamazaki I,Kiritani Y.Study on groundtunnel interactions of four shield tunnels driven in close proximity，in relation to design and construction of parallel shield tunnels[J]. Tunnelling and Underground Space Technology, 1998,13(3):289.

[9]Asaoka Akira.Observational procedure of settlement prediction[J].Soils and Foundations, 1978,18(4):87-101.

[10]Mikasa M.The consolidation of raft clay[J].Civil Engineering in Japan,Tokyo:JSCE, 1965: 21-26.

Research of analytical method for tunnel settlement and deformation of high-speed railway

PENG Yipu，ZHANG Pan, XUE Yiqi

(School of Civil Engineering，Central South University，Changsha 410075，China)

Based on assessment projects of deformation monitoring of Chang-Zhu-Tan intercity railway project, the law of development for tunnel settlement about Chang-Zhu-Tan intercity railway is investigated. According to measured data, we found that the settlement amount of the tunnel is generally small, Using the hyperbolic fitting and the gray prediction model for the same set of settlement data of the comprehensive II standard team of Chang-Zhu-Tan, the differences between measured and predicted settlement are analysed, and the applicability of two models are compared. The results show that: The simulation of hyperbolic settlement requires a lot of samples, it can be used as a method to assess the tunnel settlement. However, the high simulation accuracy is only valid in the case of a small number of incremental cumulative settlement. Grey prediction desired sample is small, and has simple operation and high simulation accuracy. Comparing with the hyperbolic fitting, gray prediction has higher precision and universality.

hyperbola; grey prediction; tunnel; settlement analysis

2015-12-27

国家自然科学基金资助项目(51378514)

彭仪普(1970-)，男，湖南长沙人，副教授，从事土木工程结构变形监测等研究；E-mail: pengyp2003@163.com

U238

A

1672-7029(2016)10-1879-07