中考题中的整式

徐智勇

中考题中的整式

徐智勇

作为初中阶段整个代数式系统的基础部分，整式有其天然的重要性，不仅让学习者初步体会到用代数思想来表达数量关系和变化规律，体会模型思想，强化符号意识，而且也为后续的分式、二次根式等代数式的学习奠定了必要的基础.中考对整式的考查也是丰富的，下面通过一些实例加以说明.

一、列代数式

例1（2016·内蒙古呼和浩特）某企业今年3月份产值为a万元，4月份比3月份减少了10%，5月份比4月份增加了15%，则5月份的产值是（）.

A.（a-10%）（a+15%）万元

B.a（1-90%）（1+85%）万元

C.a（1-10%）（1+15%）万元

D.a（1-10%+15%）万元

【分析】由题意可得：4月份的产值为a（1-10%），5月份的产值为4月份的产值×（1+ 15%），进而得出答案C.

【点评】应用性问题中，列代数式要求能够正确理解具体问题的含义，按照正确的代数式格式表达.

变式练习1（2016·安徽）2014年我省财政收入比2013年增长8.9%，2015年比2014年增长9.5%，若2013年和2015年我省财政收入分别为a亿元和b亿元，则a、b之间满足的关系式为（）.

A.b=a（1+8.9%+9.5%）

B.b=a（1+8.9%×9.5%）

C.b=a（1+8.9%）（1+9.5%）

D.b=a（1+8.9%）2（1+9.5%）

答案：C.

二、求代数式的值

例2（2016·江苏淮安）已知a-b=2，则代数式2a-2b-3的值是（）.

A.1B.2C.5D.7

【分析】直接利用已知条件a-b=2，再将原式变形为与a-b有关的式子，利用整体思想代入求出答案.

解：∵a-b=2，∴2a-2b-3=2（a-b）-3=2×2-3=1.故选A.

【点评】此题主要考查了代数式求值，利用整体思想代入求值是解题的关键.

变式练习2（2016·山东威海）若x2-3y-5=0，则6y-2x2-6的值为（）.

A.4B.-4C.16D.-16

答案：D.

三、代数式的基本运算

例3（2016·浙江舟山）计算2a2+a2，结果正确的是（）.

A.2a4B.2a2C.3a4D.3a2

【分析】相加的两项是同类项，所以根据合并同类项法则合并即可.

解：2a2+a2=（2+1）a2=3a2，故选D.

【点评】这类基础问题，只要同学们熟练掌握好与整式有关的基本法则即可.

变式练习3（2016·江苏连云港）计算：5x-3x=（）.

A.2xB.2x2C.-2xD.-2

答案：A.

四、代数上的灵活应用

例4（2016·山东临沂）用大小相等的小正方形按一定规律拼成下列图形，则第n个图形中小正方形的个数是（）.

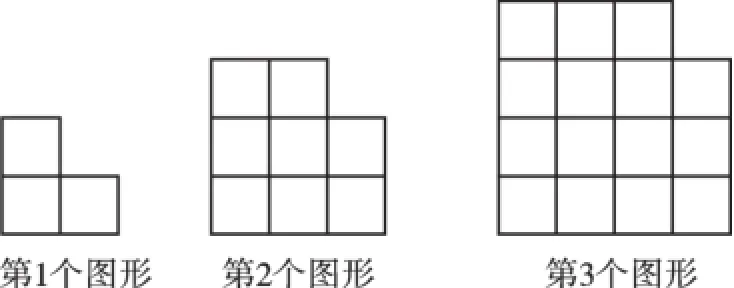
A.2n+1B.n2-1

C.n2+2nD.5n-2

【分析】由第1个图形中小正方形的个数是22-1，第2个图形中小正方形的个数是32-1，第3个图形中小正方形的个数是42-1，……，可知第n个图形中小正方形的个数是（n+1）2-1，化简可得答案.

解：因为第1个图形中小正方形的个数是22-1=3；第2个图形中小正方形的个数是32-1=8；第3个图形中小正方形的个数是42-1= 15；……；所以第n个图形中，小正方形的个数是（n+1）2-1=n2+2n+1-1=n2+2n.故选C.

【点评】解决图形的变化这种规律类问题的常用方法是考虑一些特殊情形，发现规律，作出合理的猜想，也经常要用到一些灵活的数学方法，如本例应用补形的思想将问题转化为正方形来处理就很好地降低了难度.

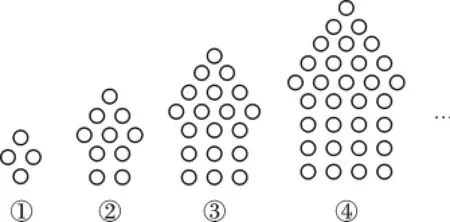
变式练习4（2016·重庆A卷）下列图形都是由同样大小的小圆圈按一定规律所组成的，其中第①个图形一共有4个小圆圈，第②个图形中共有10个小圆圈，第③个图形中一共有19个小圆圈，……，按此规律排列下去，第⑦个图形中小圆圈的个数为（）.

A.64B.77C.80D.85

答案：D.

江苏省扬州大学附属中学东部分校）

欲了解更多规律题的解析技巧，请扫二维码