动态钢轨平直度测量仪测试平台的研制

吴元良 上海铁路局科研所

动态钢轨平直度测量仪测试平台的研制

吴元良 上海铁路局科研所

测试平台模拟真实轨道设计，配有不同波长及波幅的可更换式轨面波形模拟条，满足动态钢轨平直度测量仪针对被测钢轨几种典型不平顺类型的测量需求。测试平台基于计量原理设计，通过分析其不确定度分量并合成标准不确定度用以评定测试平台的精度。通过比对国家铁道行业标准TB/T3276-2011高速铁路用钢轨规定，其结果显示测试平台的精度满足测量动态钢轨平直度测量仪的检测需求。

钢轨；平直度；测试平台；不确定度

钢轨平直度是指沿钢轨纵向轨顶面不平顺的指标，研究其意义在于更好的降低列车运行时的振动，减轻轮轨磨耗，提供乘车的舒适感和安全感。准确测量掌握轨面不平顺的实际情况也是实现对轨道不平顺状态科学评定、监控管理的前提条件。随着我国高速铁路的发展，轨面不平顺引起的轮轨冲击破坏、振动以及运行噪声等问题日益凸显，在有限的天窗时间内对钢轨不平顺进行连续在线检测是目前工务系统急需解决的问题。

动态走形式钢轨平直度测量仪可以实现钢轨平直度的连续检测，有效提高平直度检测的效率，不过由于其边走行边测量的方式，测量仪检测位置随其运动状态的改变而不同，因此需要通过不同检测方法和数学算法修正才能得到正确的检测值。例如基于惯性基准法的轨检车，基于弦测法和轴箱加速度原理开发的专用检测小车等，都采用了不同的硬件设备和数学算法。检测算法本身的正确性和检测仪器本身的准确性就显得至关重要。

但是目前对于动态平直度测量仪本身的测试，特别是检测仪器的校验缺少专门的工具和设备，也无法对波形复杂、频率（波长）宽泛等类似钢轨不平顺检测模型的准确性进行全面验证。基于上述现有技术的不足，设计一套专门的检测校验设备--动态钢轨平直度测量仪测试平台，通过设置不同波长、波幅的可更换式轨面波形模拟条，对钢轨平直度测量设备的检测算法及检测精度进行校验，以期为工务检测设备的准确性提供技术支持。

1　设计结构

测试平台基于计量原理设计，整体模拟真实轨道，分为左右双轨，间距为标准轨距1 435 mm，全长为11 m。其结构如图1所示。图中标记分别为：1轨面波形模拟条、2大理石平尺、3精调支座、4粗调支座、5底座安装板、6钢筋混凝土基座、7轨面波形模拟面。

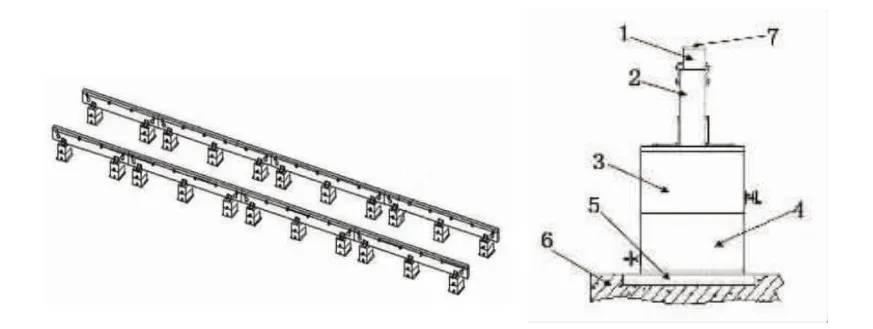
图1 测试平台结构图

1.1平台基座建设

测试平台自身的稳定性是校验准确性的前提，为防止平台在温度、载荷等因素下产生形变与沉降，其基座由钢筋混凝土加固而成。施工过程中扎钢筋笼并焊接平台底座安装板（见图2）。

图2 测试平台基座与底座安装板

1.2平台调节装置

测试平台的高低与角度调节通过安装于底座安装板上的调平支座实现。调平支座由一个粗调支座，一个精调支座构成。精调支座通过粗调支座支撑，粗调支座通过预埋铁安装板固定于钢筋混凝土基座上。通过粗调支座和精调支座的结合调整，可以快速及精准地调节平台的高度与角度（见图3）。

图3 调平支座

1.3平台基准选择

大理石平尺为天然优质石材经人工研磨而制成的精密测量工具，其质地均匀，稳定性好、强度大、硬度高，能在重负荷下保持高精度，特别适用于实验室高精度测量工作。大理石平尺物理性能如表1所示。

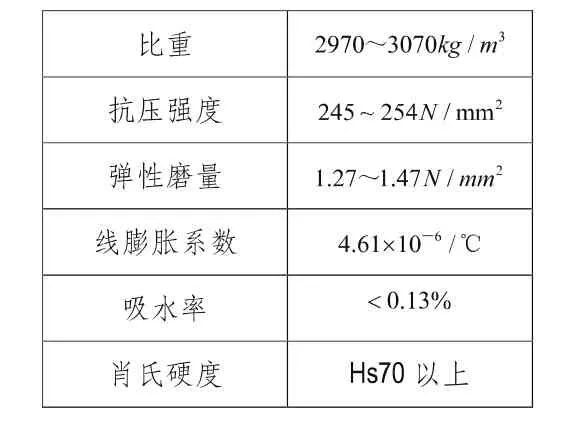
表1 大理石平尺物理特性

在调平支座上固定安装总长度为11 m的00级大理石平尺，作为测试平台的基准。大理石平尺精度参照先进国家标准，平面度公差依JB/T7975-1999标准，选择大理石平尺为

1.4平台波形设计

轨面波形模拟条由铝合金材料加工而成，放置在大理石平尺之上并通过扣件固定，保证其与大理石平尺的紧密贴合。轨面波形模拟条的表面通过精加工实现不同类型的波形模拟，可以根据需要设计成不同波幅、波长的正弦波或者不规则波形，以供使用。在系列波形设计中，结合动态钢轨平直度检测仪的尺寸及现场钢轨实际不平顺性，设计出不同波长、波幅的轨面波形模拟条，具体有正弦曲线y=0.3sin（2πx/ 300），y=0.8sin（2πx/1000），y=sin（2πx/1500），y=1.5sin（2πx/2000），y=2sin（2πx/3000）。为了更加切合现场真实情况，验证动态钢轨平直度测试仪数据处理方法的正确性，设计一组复合波，分别由不同波幅（0.3 mm，0.8 mm，3 mm）、不同波长（0.3 m，1 m，7 m）的三组正弦波叠加而成。测试平台如图4所示。

图4 测试平台

2　校验原理与过程

测试平台主要通过对比分析波形模拟条的设计波形和平直度测量仪的检测波形从而确定平直度测量仪的检测精度。具体操作如下：

（1）选择需要测量的波形，把对应轨面波形模拟条固定安装在平台大理石平尺上。

（2）以大理石平尺为水平基准，使用深度千分尺以固定间距逐点测量测试平台波形模拟面到大理石平尺的高度h，为方便比较计算，将千分尺测量数据水平翻转，得到千分尺测量曲线函数H（n），作为精度校验的基准。如图5所示。

图5 千分尺基准值

（4）操作动态钢轨平直度测量仪测量测试平台，全程记录测量数据。由于平直度测量仪的检测频率高，测量数据多，通过数据处理并筛选出与测试平台基准数据对应的检测值，将其拟合成测量仪检测值的曲线函数，记为H'（n），如图6所示。

图6 动态平直度测量仪检测值

（5）计算函数误差C（n）=/H'（n）-H（n）/，用来评价平直度测量仪的测量结果。

3　测试平台精度推导

在测量轨面波形模拟面到大理石平尺高度值h的过程中，存在不同干扰因素会影响测试平台的整体精度。需要将其分别列出并合成标准不确定度uc，取其两倍作为测试平台的扩展不确定度u用以评价测试平台整体的精度：

3.1实验室标准偏差u0的引入

在同一个位置多次测量轨面波形模拟面到大理石平尺的高度值h，计算其实验室标准差，计算公式为：

其中s（yi）为实验室标准差，这里记它为u0；yi为第i次测量值；为多次测量结果的算术平均值。

3.2千分尺引入的不确定度u1

使用深度千分尺测量轨面波形模拟面到大理石平尺的高度，根据高度值的不同需要将深度千分尺设定在不同量程挡位。不同量程对应不同的最大允许误差MPE记为m。由千分尺不同挡位引入的不确定度

3.3千分尺读数装置引入的不确定度U2

千分尺最小分度值为0.01 mm，其最小分度值的一半即为0.005 mm。记千分尺读数装置引入的不确定度为u2，则

3.4千分尺与检定器线膨胀系数不确定度引入的不确定度u3% %%%%

假设千分尺与检定器的线膨胀系数在±1×10-6C-1范围内均匀分布，其线膨胀系数差δa应在±2×10-6C-1范围内服从三角分布。该分布的半宽为2×10-6C-1，若标准温度20℃，记千分尺与检定器线膨胀系数不确定度引入的不确定度为u3，其计算公式为：u3=L（t-20）·u（δa）。其中L为千分尺测量杆的长度，t为测量时的气温，δa为千分尺与检定器的线膨胀系数差，被测距离为波形面和大理石平尺之间的高度，千分尺实测物为大理石平尺，因此线膨胀系数差为大理石平尺和千分尺之间的差值。因为服从三角分布，故

3.5千分尺与检定器间的温度差δt引入的不确定度u4%%%%

千分尺与检定器间存在温差，假设δt在等±0.3℃范围内服从均匀分布，则δt的标准不确定度u（δt）为：，于是：u4=L·a·u（δt）。其中L为千分尺测量杆的长度，a为千分尺线膨胀系数。

3.6横向间距测量误差引起的纵向误差u5% %%%%

使用钢板尺等间距划分平台的测量点，由于钢板尺存在测量误差记为σ，从而引起纵向最大误差。A为设计波形幅值，λ为设计波形波长。

3.7合成标准不确定度的评定uc%%%%%。其中u6为大理石平尺的直线度误差。选择两倍的uc作为整个平台的扩展不确定度U，其置信概率达到94.5%。

根据国家铁道行业标准TB/T3276-2011高速铁路用钢轨规定，钢轨轨顶平直度要求为≤0.2mm/1m，因此检测钢轨所用动态平直度测量仪的精度要求为。这是因为在选用测量仪器时，要遵循最大允许误差为被测对象所要求误差的1/3～1/5。同理，检测动态平直度测量仪的设备其精度必须达到。在测试平台安装不同波形轨面波形模拟条的情况下分别计算其对应的测试平台不确定度，其最大误差值为0.0175 mm，小于0.0222 mm，因此测试平台满足测量动态钢轨平直度测量仪的检测需求。

4　结束语

动态钢轨平直度测量仪测试平台结构模拟真实轨道，拥有标准轨距和11 m的长度，加强型钢筋混凝土地基有效防止外界振动干扰，为核查动态钢轨平直度测量仪的测量精度提供了一个稳定基础。平台提供不同波长、不同波幅的轨面波形模拟条，更换方便，可模拟现场钢轨轨面的不同波形，用于验证测量仪的数学模型及数据处理的正确性。平台基于计量原理设计，其最大误差值小于国家行业标准，满足测量动态钢轨平直度测量仪的检测需求，因此可以用于校验动态钢轨平直度测量仪的检测结果。

［1］胡晴莽，杜军生，洪晓东.钢轨平直度测量原理及技术应用探讨［J］.攀钢技术，2000，23（3）∶67-71.

［2］毛晓君，许玉德，周宇.基于四点弦测法的轨面不平顺检测及复原方法［J］.华东交通大学学报，2013，30（5）∶13-17.

［3］李明华，李立林，何晓源.高速铁路轨道不平顺幅值控制研究［J］.铁道工程学报，2009（9）∶26-30.

［4］张伟.基于轴箱谱的轨道短波不平顺识别方法研究［D］.北京交通大学，2008.

［5］倪育才.实用测量不确定度评定［M］.中国质检出版社，2014.

［6］中国计量测试学会组.一级注册计量师基础知识及专业实务［M］.中国质检出版社，2013.

［7］同济大学概率统计教研组.概率统计［M］.同济大学出版社，2013.

［8］中华人民共和国铁道部.TB/T 3276-2011高速铁路用钢轨［S］.中国铁道出版社，2011.

责任编辑：宋飞 张建强

来稿时间：2016-05-13