布尔函数的互相关系数的一些性质

于瑞瑞，卓泽朋，任明生

（淮北师范大学数学科学学院，安徽淮北235000）

布尔函数的互相关系数的一些性质

于瑞瑞，卓泽朋，任明生

（淮北师范大学数学科学学院，安徽淮北235000）

利用nega相关系数的已有结论，给出布尔函数的互相关系数与其他一些密码学性质之间的关系，在此基础上，得出了4个布尔函数的nega互相关系数之间的关系.

布尔函数；互相关系数；nega互相关系数

0 引言

为了使全局雪崩准则（GAC）能达到一个更好的折衷效果，在互相关系数的基础上提出两个指标σf和Δf，因为σf和Δf越小，布尔函数的GAC性质就越好.文献［1］给出这两个指标的上下界：22n≤σf≤23n，0≤Δf≤2n.文献［2］给出平衡布尔函数的σf指标下界为：σf≥22n+2n+3.文献［3］也给出n元布尔函数f（）x在Fn2的一个子集上满足扩散准则时的σf指标下界.文献［4］研究关于nega-Had⁃ amard变换的一些性质.

本文首先给出一些布尔函数的基本概念和符号说明，然后研究关于互相关系数的一些扩展知识.

定义1［5］设f（）x，g（）x是Βn上的布尔函数，在a处的互相关系数.当f（）x=g（）x，称Δf，f（）a为f（）x在a处的自相关系数，简记为Δf（）a.

定义4［2］设f（x）是Βn上的n元布尔函数，称分别为f（x）的平方和指标和绝对值指标.

推论1任一Βn上的n元布尔函数f（x）是平衡的当且仅当

引理1［5］设是Βn上的n元布尔函数，则

定义5［6］设是Βn上的n元布尔函数，记的Fourier变换.此外，与汉明重量之间的关系为：

定义6设f（x）是Βn上的n元布尔函数，若g（x）∈Βn使得f（x） g（x）=0，则称g（x）为f（x）的一个零化子.记为f（）x的所有零化子构成的集合.称AI（）f=min｛AN（）f， AN（）f⊕1｝为f（）x的代数免疫度.此外，AI（）f和wt（）f之间的关系可描述为在此基础上，可以得到互相关系数与代数免疫度之间的制约关系为

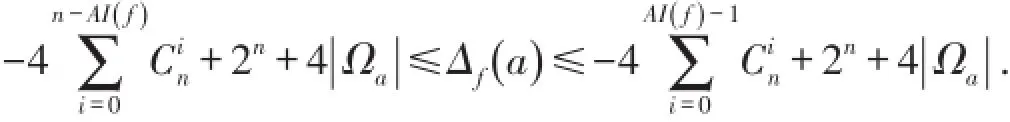
1 Nega-Hadamard变换和nega互相关系数的性质

为方便起见，首先介绍一些关于nega-Hadamard变换的相关知识.

Βn上的n元布尔函数f（x）在任意点处的Walsh-Hadamard变换定义为

命题1设f（x），g（x）是Βn上的n元布尔函数，则

接下来，从一些特殊情况研究nega互相关系数的一些性质，其中包括4个布尔函数的nega互相关系数.

定理1设fi（）x∈Βn，i=1，2，3，4，则

证明通过nega互相关系数的定义，对于任意u∈Fn2，我们有

证毕.

在定理1中，若f1=f3，f2=f4，则

特别地，若u=0，可得到如下结论.

推论2设f1，f2∈Βn，则

注意到（1）式给出了NCf1，f2和NCf1，NCf2之间的关系.

在定理1中，若f2=f4，则可得

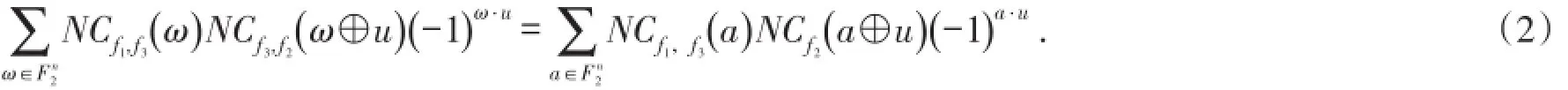
因为

因此（2）式可另写为

其中u¯=1⊕u.

［1］ZHANG Xianmo，ZHENG Yuliang.GAC-the criterion for global avalanche characteristics of cryptographic functions［J］. Journal of Universal Computer Science，1995，1（5）：320-337.

［2］SON J J，LIM J I，CHEE S，et al.Global avalanche characteristic and nonlinearity of balanced Boolean function［J］.Informa⁃tion Processing Letters，1998，65（3）：139-144.

［3］SUNG S H，CHEE S，PARK C.Global avalanche characteristics and propagation criterion of balanced Boolean functions［D］.Information Processing Letters，1999，69（1）：21-24.

［4］卓泽朋，崇金凤，魏仕民.Nega-Hadamard变换和negabent函数［J］.山东大学学报（理学版），2013，48（7）：29-32.

［5］ZHOU Yu，XIE Min，XIAO Guozhen.On the global avalanche characteristics between two Boolean functions and the higher order nonlinearity［J］.Inf Sci，2010，180（2）：256-265.

［6］SARKAR P，MAITRA S.Cross-correlation analysis of cryptographically useful Boolean functions and S-boxes［J］.Theory of Computing Systems，2002，35（1）：39-57.

［7］SU Wei，POTT A，TANG Xiaohu.Characterization of negabent functions and construction of bent-negabent functions with maximum algebraic degree［J］.IEEE Transformation on Information Theory，2013，59（6）：3387-3395.

［8］CANTEAUT A，CARLET C，CHARPIN P，et al.On cryptographic properties of the cosets of RM（1，m）［J］.IEEE Transac⁃tions on Information Theory，2001，47（4）：1494-1497.

Some Properties of the Cross-correlation Coefficient of Boolean Functions

YU Ruirui，ZHUO Zepeng，REN Mingsheng
（School of Mathematical Sciences，Huaibei Normal University，235000，Huaibei，Anhui，China）

Firstly，the relationships between the cross-correlation coefficient and some other cryptographic properties of Boolean functions are presented.On this basis，some known knowledge concerning the negacrosscorrelation coefficient is summarized.Then the link among nega-crosscorrelation coefficient of four Bool⁃ean functions is given.

Boolean function；cross-correlation coefficient；nega-crosscorrelation coefficient

TN 918.1

A

2095-0691（2016）03-0024-04

2016-04-12

安徽省自然科学基金资助项目（1608085MF143）；安徽高校省级自然科学研究重点项目（KJ2014A220）；安徽高校优秀青年人才支持计划重点项目（gxyqZD2016112）

于瑞瑞（1990-），女，河南周口人，硕士生，研究方向：密码学；通讯作者：卓泽朋（1978-），男，安徽灵璧人，副教授，研究方向：密码学.