Efficient characterization for M｛2,3｝，M｛2,4｝and M｛2,3,4｝

ZHENG Dao-sheng

（Department of Mathematics，East China Normal University，Shanghai200241，China）

Efficient characterization for M｛2,3｝，M｛2,4｝and M｛2,3,4｝

ZHENG Dao-sheng

（Department of Mathematics，East China Normal University，Shanghai200241，China）

Article ID：1000-5641（2016）02-0009-11

集合A到集合B上的一个一一映射f称为B的一个有效刻画.本文提出的选逆象指标法（SIIIM）给出集到象集的一个有效刻画公式，并证明了B1是I｛2，3｝s的稠密子集，且I｛2，3｝s的每个元素都与B1的某个元素置换相似.利用上述结果，分别建立了I｛2，3｝和长方阵广义逆矩阵类M｛2，3｝的有效刻画公式.再利用等式I｛2，3｝s=I｛2，4｝s=I｛2，3，4｝s，进一步获得了M｛2，4｝，M｛2，3，4｝的有效刻画公式.算法3.1可用于无重复地计算I｛2，3｝s的任一个元素.

广义逆的有效刻画；矩阵的奇异值分解；正交投影矩阵；映射公式的逆象指数集；稠密子集

0　Introduction

Reference to the glossary of notation in［1］，some notations are described here∶

（a）The four Penrose equations can be written as∶For each M∈Cm×n，we have M｛1｝=｛X∶MXM=M｝；M｛2｝=｛X∶XMX=X｝；M｛3｝=｛X∶MX=（MX）∗｝；M｛4｝=｛X∶XM=（XM）∗｝.

（b）M｛2,3,4｝s=｛X∶rank（X）=s,X∈M｛2｝∩M｛3｝∩M｛4｝｝.

（c）The t×t identity matrix is denoted as Itor I.The set of all n×s isometric matrices is denoted as ISMn,s=｛Z∶Z∈Cn×s,Z∗Z=Is｝.The set of all n×n orthogonal projection matrices is denoted as OPMn=｛Y∶Y=Y∗=Y2∈Cn×n｝.

（d）Let M=（mp,q）∈Cm×n,1≤i1＜···＜ik≤m,1≤j1＜···＜jh≤n，then M（i1, ···,ik；j1,···,jh）≜（mit,jl）is called a k×h submatrix of M.Especially，M（i1,···,ik；1,2,···, n）is denoted as M（i1,···,ik）.The square matrix M（i1,···,ik；i1,···,ik）is called a k×k principle submatrix of M.

The problem of efficient characterization for a class of generalized inverse matrices is described in［1，§2.8］.Reference to Ben-Israel's term，a definition is given here.

Definition 0.1Let a characterization formula（CF）from a set X with nxvariables ontoAccording to［1］，this CF has ns arbitrary parameters）.If for each β∈B，the inverse image set f-1（β）=｛α∶f（α）=β,α∈X｝has just one element， then f（X）is called an efficient characterization formula（ECF）.If there exists β∈B such that f-1（β）is an infinite set，then f（X）is a nonefficient formula（NECF）.

For a NECF，as α ranges over the entire set X，then there exists β∈B such that this β will be obtained repeatedly an infinite number of times！And the NECF must have redundant arbitrary parameter.

In［1］，four ECFs for M｛1｝,M｛1,3｝,M｛1,4｝and M｛1,2｝are given.has the SVD∶is given.Two characterization formulas for M｛1｝are

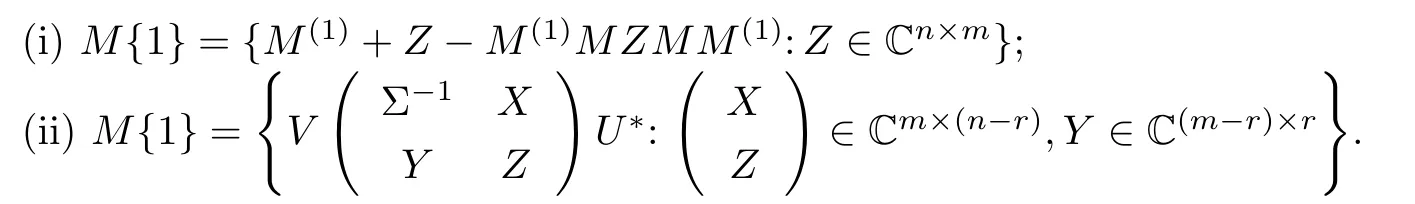
We know formula（i）is just（2.4）in［1］，and it has nm arbitrary parameters.Formula（ii）has nm-r2arbitrary parameters and is an ECF for M｛1｝.So（i）has r2redundant arbitrary parameters and is a NECF.The last fact shows that compared with a relevant NECF for B，the first merit of an ECF is that it has no redundant arbitrary parameters.We further find that the ECF can be used to more penetratingly and distinctly reveal the structure of set B.Notice that the number of the arbitrary parameters in an ECF B=fe（Xe）is less than that in the relevant NECF B=f（Xne）.When an element of B is computed，the number of arithmetical operation of fe（Xe）is denoted as newhile the relevant number of the NECF is denoted as nne. Generally we have ne＜nne.In other words，the computational complexity neof fe（Xe）is less than nne.

If the redundant arbitrary parameters in a NECF are eliminated， an ECF will be estab lished.The problem is how can we eliminate the redundant arbitrary parameters.A natural idea is if in each inverse image set f-1（β）of a given β，an index element αβ∈X is selected，and all these index elements form a inverse image index set XB⊂X，then we obtain an ECF B=f（XB）.The above idea is temporarily called as selecting inverse image index method（SIIIM）.

Notice that M｛1｝is the solution set of a linear matrix equation MXM=M while M｛2｝is the solution set of a nonlinear matrix equation.So establishing an ECF for M｛2｝might be more difficult than that for M｛1｝.

After an ECF for M｛2｝is given in［6］，in this paper three ECFs for M｛2,3｝，M｛2,4｝and M｛2,3,4｝are established respectively.

We first consider the case of M｛2,3｝.Theorem 2.1 shows that each CF for I｛2,3｝scan be used as a base of a CF for M｛2,3｝.Lemma 1.1 means if I=In，then Y∈I｛2,3｝⇐⇒Y=Y2=Y∗∈OPMnand

Theorem 2.6 and 2.7 in［1］show that if 0then

We find that in（0.2），if M=I，then we obtain（0.1）.We can show that（0.2）and（0.3）are two NECFs.

If the current result Lemma 1.1（4）is used to generate the isometric matrix Z1∈ISMn,s，then Theorem 1.1 is a SIIIM，and is an ECF from A1onto B1（see Definition 1.1（4））.Theorem 1.2 shows that B1is a proper subset of I｛2,3｝sand I｛2,3｝sis the union set of its some subsets，and each of these subsets is isometry with B1.And each element of I｛2,3｝sis permutation similar to an element of B1.Then the ECFs for I｛2,3｝s,I｛2,3｝are established respectively.

Theorem 1.3 shows that B1is a dense subset of I｛2,3｝s.

The ECFs for M｛2,3｝，M｛2,4｝and M｛2,3,4｝are obtained in§2 respectively.

A feasible algorithm，Algorithm 3.1，is designed in§3.It can be used to realize（1.3（ii））.

1　Efficient characterization for I｛2,3｝

Lemma 1.1Assume I=In.Then

（1）I｛2,3｝=I｛2,4｝=I｛2,3,4｝=｛Y∶Y2=Y=Y∗∈Cn×n｝=OPMn.

（2）I｛2,3｝0=I｛2,4｝0=I｛2,3,4｝0=｛0｝，I｛2,3｝n=I｛2,4｝n=I｛2,3,4｝n=｛In｝.

（5）Y2=Y=Y∗such that Y=ZZ∗and Z∗Z=Is.

Proof（1）By the Penrose equations，it is easy to prove（1）.

The proofs of（2）and（4）are omitted.

（5）“⇐”When Y=ZZ∗，and Z∗Z=Is，we have Y2=Y=Y∗.

“⇒”Since Y∗=Y，we can assume that the SVD of Y iswhere U=（U1,U2）satisfiesThen Y=Y2means Σs=I and

Definition 1.1Assume 0＜s≤n.

（3）Ii,jis obtained by exchanging the i,j-th rows of I.Define

（4）For any n,s with 0＜s＜n，define

Theorem 1.1Let β=Y Y∗,Y=Y（1,···,n）∈Then

（1）β2=β=β∗⇐⇒Y∗Y=Is.

Proof（1）Lemma 1.1（5）means（1）holds.

（2）Lemma 1.1 means Y∗Y=Is.It is obvious that W（1,···,s）⇐⇒ Y（1,···,s）If Y（1,2,···,s），set η=Y（s+1,···,n）Y-1（1,2,···,s），α∗=（Is,η∗）∈A1，we obtain β=Y Y∗=f（α）∈B1.Conversely，if β=Y Y∗∈B1with Y（1,···,s）∈t＜s，then（Is+η∗η）-1=Y（1,···,s）∗Y（1,···,s）.This contradiction means（1.1）holds.

Remark 1.1（1）（1.2）is an ECF from A1onto B1and it has（n-s）s arbitrary parameters while（0.1）has ns arbitrary parameters.Later，this result is enlarged to the I｛2,3｝scase，and we will show I｛2,3｝s≠B1⊂I｛2,3｝s.

（2）Denote W1=｛W∶W（1,···,s）∈Y1=｛Y∶Y∈Cn×s,Y（1,···,s）∈,Y∗Y =Is｝.Then βw=W（W∗W）-1W∗=WW†，βy=Y Y∗=Y Y†and βα=α（α∗α）-1α∗=αα†are three FCs for the orthogonal projection matrix set B1⊂OPMn，where α=（Is,ηT）T∈Cn×s∈A1.Then in Theorem 1.1，A1is the inverse image index set of B1with respect to the original image set Y1or W1，and the ECF βαis a SIIIS.

（1）Assume L（i1,···,is）=Is，i.e.，lij=j=1,···,s，whereis the j-th row of Is. Denote Gt=L（1,2,···,it-1）∈（i1=1 means G1=Ø），（e.g.，assume n=8，s=3，i1=2，i2=4，i3=7，then G1=（l1），G（1）=L（1,4,7），G2=L（1,2,3），G（2）=L（1,2,3,7），G3=L（1,2,3,4,5,6），G（3）=G3）.Then Lfns=L（i1,···,is）⇐⇒ the t-th column of G（t）（denoted as g（t））is 0，t=1,2,···,s⇐⇒ the t-th column of Gt（denoted as gt）is 0 or Ø，t=1,2,···,s.

Proof（1）It is easy to show that g（t）=0 if and only if gt=0 or Ø，t=1,···,s.Thus，for any t，the row intersection set of L（i1,···,is）（=Is）and G（t）has s-1 rows，they form a matrixThe t-th column ofis zero.Assume that g（t）has a component lh,t≠0，then lhis not a row ofObviously，h＜it.

（i）If h＜i1，then（h,i1,···,it-1,it+1,···,is）≺（i1,···,is），and we have L（h,i1,···,it-1, it+1,···,is）∈This is a contradiction.

（ii）If ik＜h＜ik+1≤it-1，then（i1,···,ik,h,ik+1,···,it-1,it+1,···,is）≺（i1,···,is），and L（i1,···,ik,h,ik+1,···,it-1,it+1,···,is）∈，also a contradiction.

（iii）If it-1≤h＜it，then（i1,···,it-1,h,it+1,···,is）≺（i1,···,is），and L（i1,···,it-1,h, it+1,···,is）is nonsingular.Again，we obtain a contradiction！So we obtain g（t）=0，t=1, ···,s.

“⇐”We want to prove that if（j1,···,js）≺（i1,···,is）then L（j1,j2,···,js）is singular. For example，assume js=is,js-1＜is-1，i.e.，（j1,···,js）≺（i1,···,is），then L（j1,···,js）is a s×s submatrix of G（s-1）.Hence L（j1,···,js）is singular.And so forth.Thus Lfns= L（i1,···,is）.

（2）An example is used to explain our conclusion.

Assume n=4 and s=2.Then we obtain Pφ（2,4）=I1,2I2,4，（Pφ（2,4）L）（2,4）=（2,4）=L（1,2），and

Theorem 1.2Let L=L（1,···,n）∈，β=LL∗，L∗L=Is.Then

（2）Bl⊂I｛2,3｝s，1≤l≤g，and B1is a proper subset of I｛2,3｝swhen s＜n.

（3）We have

Proof（1）Lemma 1.2 and Theorem 1.1 mean L（i1,···,is）=（1,···,s）∈⇐⇒∈B1⇐⇒ β∈Bφ（i1,···,is）.

（3）For each β=LL∗∈I｛2,3｝swith L∗L=Is,L∈one can always find a submatrix L（i1,···,is）∈So by（1），β∈=Bl.Thus（1.3（i））and（1.3（ii））hold.

Remark1.2（1）Theorem 1.2 means I｛2,3｝sis completely dependent on s（n-s）arbitrary parameters while the formula in Lemma 1.1（3）has ns arbitrary parameters and has s2redundant arbitrary parameters.

（2）Given a permutation matrix P and a matrix X，we have‖PXPT‖2=‖X‖2［1,4］.So（1.3（i））means I｛2,3｝sis the union set of its g isometry subsets.In fact if β∈I｛2,3｝s，then there exists γ∈B1such that β=PγPT，where P∈Pn,s.

Although（1.3（i））has no redundant arbitrary parameter，but it is a multivalue mapping from A1onto I｛2,3｝sand Definition 0.1 is not suitable for it.When n＞s＞0，l≠t，we can showand some repeated computation may appear when some elements of I｛2,3｝sare computed by（1.3（i）），e.g.，set n=3，s=1，By（1.3（i）），β may be computed three times.

（1.3（ii））is a single valued mapping from A onto I｛2,3｝sand it is an ECF.In§3，an algorithm，Algorithm 3.1，is designed to realize（1.3（ii））concretely.

（3）From Lemma 1.1（3），Theorem 2.1 and Theorem 2.2，two kinds of computation formulas for β∈I｛2,3｝sare established.They are βy=Y（Y∗Y）-1Y∗and βα=α（α∗α）-1α∗，where α∗=（Is,η∗），Y∈It is already shown that βyis a NECF，while βαis an ECF and it is a special case of βy.In order to obtain a βy∈B1，we must test the rank of Y while we always have rank（α）=s.

From the numerical computation point of view［1,3］，the representation βαis sometimes numerical unstable，because sometimes，the numerical result of α∗α might be a singular or illconditioned matrix.In order to overcome this difficulty，two plans proposed here∶（i）Assumethat the SVD of α isthen α（α∗α）-1α∗is replaced by（ii） Compute an orthogonal decomposition of α=QR=Q1R1，R1∈by Householder or Civens transformations.Then we have α（α∗α）-1α∗=Generally，the SVD method has higher precision while the orthogonal decomposition method has lower computation complexity. Details of this problem are omitted here.

Theorem1.3Given n,s，0＜s＜n.Then in the metric spaces，B1is a dense subset of I｛2,3｝s.

This theorem tells us that sometimes，only the elements of B1need be computed.In this case Algorithm 3.1 can be simplified greatly！

2　Efficientcharacterization　ofM｛2,3｝,M｛2,4｝　and M｛2,3,4｝

Theorem 2.1Let the SVD of M∈be＞···＞σt＞0，whereV∗V=In.Then

（2.1）is an ECF and has（r-s）s+（n-r）s=（n-s）s arbitrary parameters.But（0.2）has ns arbitrary parameters.

（2.2）is an ECF and has（r-s）s+（m-r）s=（m-s）s arbitrary parameters.But（0.3）has ms arbitrary parameters，and it is a relevant NECF of（2.2）.

（4）We have

Theorem 1.1 and Theorem 1.2 mean that if we take α=（Is,η∗η）T∈（Z1）l=thenl=1,···,gr,s，is an ECF from A⊂onto I｛2,3｝s.Hence（2.1）holds.

（3）We know（2.3）holds⇐⇒ （2.1）and（2.2）hold.Thus X∈I｛2,3,4｝）⇐⇒ X12=0,We then obtainDenote

From the fact σi≠σjwhen i≠j,1≤i,j≤t，we obtain=（σi/σj）Qi,j=（σj/σi）Qi,j,Qi,j=0 when i≠j,1≤i,j≤t.So=diag（Q11,···,Qtt）.The fact（ΣX11）2= ΣX11means σiQii=（Qiiσi）∗=（σiQii）2.

From Theorem 1.1 and Theorem 1.2，we obtain（2.3）.If t=r，then r1=···=rt=1，and we obtain σiQii=（1）or（0）,i=1,···,r（=t）.So M｛2,3,4｝has just 2relements.

（4）We know（2.3）and MXM=M mean（2.4）holds.

Remark 2.1（1）Through a complex deducing process，a characterization for M｛2,3,4｝is given in Ben-Israel's book（cf.［1，Ex.2.72-2.77］）.

But the efficiency of（2.7）is not considered there.

（2）By the way，the result‘M｛2,3,4｝has 2relements⇐⇒ t=r'is just the conclusion of［1，Ex.2.76］.

3　An algorithm

Now we prepare to design an algorithm to realize（1.3（ii））concretely.

In Definition 1.1（1），for each α=（i1,···,is）∈O（n,s），the function value l=φ（α）can be obtained recursively by following relations∶

（r-i）s=1 means φ（i1）=i1,1≤i1≤n.

（r-ii）Given s＞1.If for some p，we have 1≤p≤s≤n，ik-1+1=ikwhen k≤p，and ip+1＜ip+1，then φ（i1,···,is）+1=φ（1,···,p-1,ip+1,ip+1,···,is）.Especially we have φ（1,···,s）=1,φ（is-s+1,is-s+2,···,is）=gis,s,and φ（n-s+1,···,n）=gn,s.

（r-iii）If s＞p≥1 and（i1,···,ip,ip+1,···,is）∈O（n,s）with ip+1＜ip+1,ik+1=ik+1when s≥k≥p+1，then φ（i1,···,is）=φ（is-s+1,···,is）-（φ（is-s+1,···,is-s+p）-φ（i1,···,ip））=gis,s-gis-s+p,s-p+φ（i1,···,ip）.For example，φ（2,3,5,6）=φ（3,4,5,6）-（φ（3,4）-φ（2,3））=15-（6-3）=12.φ（2,4,6）=φ（4,5,6）-（φ（4,5）-φ（2,4）），φ（2,4）= φ（3,4）-（φ（3）-φ（2））=6-（3-2）=5,φ（4,5）=10，φ（4,5,6）=20.So φ（2,4,6）=15.Indeed，in Table 1，we have φ（2,3,5,6）=12 and φ（2,4,6）=15.

Definition 1.1（1）also means for given s≤ n,andthe functionsatisfiesis the inverse function of φ.if n＜m，thenl= 1,···,gn,s.So for given s＜+∞，we can assume that an increasing function φsis defined onThus，a table，Table 1，can be designed as follows∶when l≥1， the（l+1,1）entry is the inverse function value l=where αl=（i1,···,is）is the l-th‘smallest'element of Os.The（l+1,s+1）entry is（i1,···,is）.

Lemma3.1Let α=Y=（Is,ηT）T∈A1，β1（α）=f（α）=f（Y）=Y（Y∗Y）-1Y∗∈B1.βl（α）Then

Proof The proof of the lemma is omitted.

Algorithm 3.1 Given n,s satisfy 0＜s＜n.As α ranges over the entire class A，we can‘efficient'obtain I｛2,3｝s.

Step 1 For l=1,2,···,gn,s，compute Pl.As the first point，take an element α=Y=（Is,ηT）T∈A1.

Tab.1　Function φsand

Tab.1　Function φsand

ls　1　2　3　4　··· 1　（1）　（1,2）　（1,2,3）　（1,2,3,4）　··· 2　（2）　（1,3）　（1,2,4）　（1,2,3,5）　··· 3　（3）　（2,3）　（1,3,4）　（1,2,4,5）　··· 4　（4）　（1,4）　（2,3,4）　（1,3,4,5）　··· 5　（5）　（2,4）　（1,2,5）　（2,3,4,5）　··· 6　（6）　（3,4）　（1,3,5）　（1,2,3,6）　··· 7　（7）　（1,5）　（2,3,5）　（1,2,4,6）　··· 8　（8）　（2,5）　（1,4,5）　（1,3,4,6）　··· 9　（9）　（3,5）　（2,4,5）　（2,3,4,6）　··· 10　（10）　（4,5）　（3,4,5）　（1,2,5,6）　··· 11　（11）　（1,6）　（1,2,6）　（1,3,5,6）　··· 12　（12）　（2,6）　（1,3,6）　（2,3,5,6）　··· 13　（13）　（3,6）　（2,3,6）　（1,4,5,6）　··· 14　（14）　（4,6）　（1,4,6）　（2,4,5,6）　··· 15　（15）　（5,6）　（2,4,6）　（3,4,5,6）　··· ... ... ... ... ... ...

Step 2 Compute β1（α）=（Is,ηT）T（Is+η∗η）-1（Is,η∗），and β1is stored.

Step 3 For l=2,···,gn,scompute Yl==PlY.Assume Pl=For Yl.if in G（t）,g（t）equals 0,t=1,···,s,then compute

Step 4 If the stop condition is not satisfied，take next element of A1.Go to Step 2.

Step 5 End.

Theorem 3.1When α ranges over the entire class A1Algorithm 3.1 can be used to efficiently realize（1.3（ii））.

ProofIn Step 2，α=（P1Y）=Y1∈A1is used to compute β1（α）=f（α）∈B1=C1.So as α ranges over the entire class A1，each element of C1will be obtained just at a time.In Step 3，when h=2，P2α=Y2is considered.According to Lemma 1.2（1），for Y2，only when g（t）=0, t=1,···,s，is computed.It means each element of B2may be observed at a time，only when this observed element is an element of C2，then it is computed and stored.

When 2＜h≤s，using Lemma 1.2（1）we can also show that each element of Chis computed at just a time.

In a word，Algorithm 3.1 is an‘efficient'characterization from

Remark 3.1We can show that in Step 3 of Algorithm 3.1，the work to test‘whether or not g（t）=0,t=1,···,s'can be deleted in most cases（see Example 3.1 and Lemma 3.2）.

Lemma 3.2Let Y=Y（1,···,n）=（yi,j）∈A1（i.e.，Y（1,2,···,s）=Is）.For each（i1, ···,is），assume Pl=Pφ（i1,···,is）,l＞1，and Yl=PlY=（（yl）i,j）∈Al.Denote（gl）t=（（yl）1,t, ···,（yl）it-1,t），t=1,···,s.Then ys+1,s≠0 means（gl）s≠0，l=2,···,g.

ProofNotice that（gl）shas is-1 components.It is easy to show if l＞1，then is≥s+1. And is≥s+1 means ys+1,sis a component of（gl）s.

Example 3.1To observe Algorithm 3.1 by some numerical examples.Assume n=4，s=2.Then gn,s=6，φ（1,2）=1，φ（1,3）=2，φ（2,3）=3，φ（1,4）=4，φ（2,4）=5，and φ（3,4）= 6.P1=Pφ（1,2）=I4，P2=Pφ（1,3）=I2,3=（e1,e3,e2,e4），P3=Pφ（2,3）=I1,2I2,3=（e2,e3,e1,e4），P4=Pφ（1,4）=I2,4=（e1,e4,e3,e2），P5=Pφ（2,4）=I1,2I2,4=（e2,e4,e3,e1）and P6=Pφ（3,4）= I1,3I2,4=（e3,e4,e1,e2）.

In α（1）case，（α（1）∗α（1））-1=I2.For βl（α（1））=f（αl（1）），l=2,···,6，we find=0，l= 2,···,6，t=1,2.For example，when l=3，α3（1）=P3α（1）=Then i1=2，β3（α（1））=（0,e2,e3,0）.So βl（α（1））=f（αl（1））are all computed for any l≥1.

In α（3）case，it is easy to show that each of the 2×2 submatrix of α（3）is nonsingular. So only β1（α（3））is computed.Of course，by Lemma3.2，from the fact that the（3，2）element of α（3）is nonzero，we can also say that only β1（α（3））needs to be computed.

［References］

［1］BEN-ISRAEL A，GREVILLE T N E.Generalized Inverse：Theory and Applications（2nd Edition）［M］.New York：Springer-Verlag，2003.

［2］BUSINGER P A，GOLUB G H.Algorithm 358，singular value decomposition of a complex matrix［F1，4，5］［J］. Comm Assoc Comp Mach，1969，12（10）：564-565.

［3］GOLUB G H，VAN LOAN C F.Matrix Computations（3rd Edition）［M］.Baltimore：Johns Hopkins University Press，1996.

［4］GOLUB G H，KAHAN W.Calculating the singular value and pseudo-inverse of a matrix［J］.SIAM J Num Anal Ser，1965，2（2）：205-224.

［5］HORN R A，JOHNSON C R.Matrix Analysis［M］.Cambridge：Cambridge University Press，1990.

［6］ZHENG D S.Efficient characterization for I｛2｝and M｛2｝［J］.J East China Normal University，2015，179（1）：42-50.

（责任编辑：林磊）

In this paper，by selecting inverse image index method，an efficient characterization formula from setonto setis given.Besides，it is shown that each element of I｛2，3｝sis permutation similar to an element of B1.Then efficient characterization formulas for I｛2，3｝and M｛2，3｝are obtained respectively.An interesting thing is B1is a dense subset of I｛2，3｝s. The fact that I｛2，3｝s=I｛2，4｝s=I｛2，3，4｝senables us to obtain the efficient characterization formulas for M｛2，4｝and M｛2，3，4｝fluently.Algorithm 3.1 may be used to compute elements of I｛2，3｝sand to avoid the repeated computation work.

efficient characterization of classes of generalized inverses；singular value decomposition（SVD）；orthogonal projection matrix；inverse image index set of a mapping formula；dense subset

O151.21；O177.7Document code：A

M｛2,3｝,M｛2,4｝和M｛2,3,4｝的有效刻画

征道生

（华东师范大学 数学系，上海200241）

10.3969/j.issn.1000-5641.2016.02.002

2014-08

征道生，男，教授，研究方向为数值代数与矩阵论.E-mail：dszheng@math.ecnu.edu.cn.