一种变步长凸组合自适应滤波算法及其性能分析*
王 蒙,赵建平,杨恒耀
(曲阜师范大学 物理工程学院,山东 曲阜 273165)
一种变步长凸组合自适应滤波算法及其性能分析*
王 蒙,赵建平,杨恒耀
(曲阜师范大学 物理工程学院,山东 曲阜 273165)
为了进一步解决收敛速度与稳态误差之间的矛盾,提高自适应滤波算法性能,将变步长算法引入到凸组合自适应滤波算法(CLMS)中,提出了一种新的变步长凸组合最小均方算法(NVSCLMS)。该算法用一种基于块步长思想的变步长算法代替原CLMS算法中的快速收敛算法。通过理论推导和仿真对比分析:提出的算法提高了CLMS算法的灵活性和实用性,且在收敛速度、稳态误差和跟踪性三个方面展现出优于变步长算法、CLMS算法和已提出变步长凸组合算法的滤波效果。
自适应滤波;CLMS;变步长算法;块步长;NVSCLMS
近年来,利用并行思想提出了凸组合最小均方[2-3](Convex Combination of Least Mean Square,CLMS)算法,进一步优化了单一变步长LMS算法的性能。该算法是将两个不同迭代步长的LMS算法滤波器(快速滤波器和慢速滤波器)进行并联,通过联合参数进行控制:算法收敛初期,快速滤波器起主要作用,以达到快速收敛的目的;等进入稳定阶段,慢速滤波器起主要作用,使总的稳态误差降低。但是,不同迭代步长的并行计算往往对算法参数的要求比较精确,而且不利于滤波器在噪声环境中保持良好的性能。同时,对于时变环境,CLMS算法还存在一定不足。因此,本文在原有CLMS算法的基础上,用一个基于块步长思想的变步长LMS算法[4]去替代CLMS算法中的步长较大的快速收敛算法。这样在提高收敛速度、降低稳态误差的前提下,增强了算法的跟踪性能,同时提高了CLMS算法的应用空间。
1 CLMS算法的介绍
CLMS算法的核心思想:利用并行思想将两个相互独立的LMS滤波器并联,并将两个滤波器分别设为快速滤波器和慢速滤波器(为了讨论方便,本文将第一个LMS滤波器看作是快速滤波器),最终通过联合参数λ(n)协调两个LMS滤波器的权重,使整个CLMS算法既可以通过快速滤波器达到快速收敛的效果,也可以通过慢速滤波器得到较小的稳态误差。整个滤波过程可发挥不同滤波器的优势,达到快速稳定的工作效果。
CLMS滤波器原理示意图如图1所示。

图1 CLMS滤波器的原理
其中,x(n)为系统输入,d(n)为期望信号;wi(n)、yi(n)、ei(n)(i=1,2)分别为两个独立LMS滤波器的权向量、输出和误差;λ(n)为CLMS算法的联合参数;y(n)为整个滤波器的等效输出;e(n)为整个滤波器的等效误差。
对于单个的LMS滤波器,工作原理如下:

其中,i=1,2。
对于组合滤波器,等效输出和等效误差为:

算法初期,λ(n)取值从1开始逐渐变小,此时快速滤波器起主要作用,以提高收敛速度。随着迭代的进行,λ(n)逐渐变小至0,慢速滤波器起主要作用,以降低整个滤波器的稳态误差。运算中,通常不直接调整联合参数λ(n),而是根据Sigmoid函数定义变量a(n)来控制联合参数,从而控制组合滤波器的工作。因此,联合参数λ(n)∈[0,1]定义为:

参数a(n)以最小均方误差为准则,采用最速下降法来调整,使组合滤波器的误差平方最小。因此,a(n)的更新公式如下:
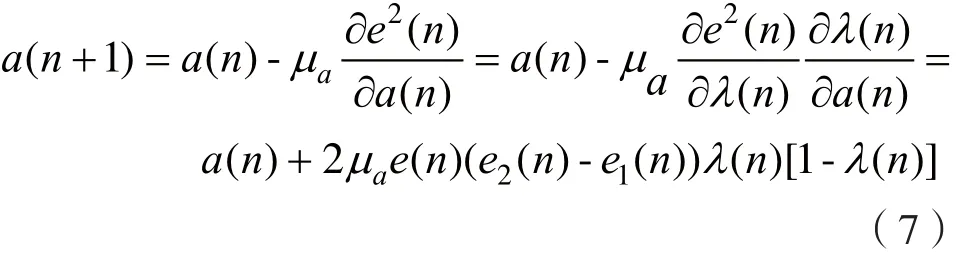
其中μa为算法的步长因子。
2 NVSCLMS算法
2.1 VSCLMS算法的提出
虽然CLMS算法在一定程度上提高了变步长LMS算法的性能,但是在某些方面仍然存在不足:①CLMS算法是两个LMS算法的并行计算,往往对算法参数的要求比较精确,因此CLMS算法对于λ(n)过于依赖;②两个固定步长LMS算法组成的CLMS,在噪声环境中无法保持良好的性能;③对于时变环境,CLMS算法灵活性和跟踪性较差。
针对CLMS算法体现的不足,部分学者将变步长思想引入到CLMS算法,提出了VSCLMS算法。VSCLMS算法即在CLMS算法的基本原则下,用变步长LMS算法代替原CLMS算法中较大步长LMS算法,以提高算法的灵活性和抗干扰性,同时不影响系统的稳态误差。文献[5-7]所提出的算法,就是分别将基于Sigmoid函数、洛伦兹函数、双曲正切函数的变步长函数带入到CLMS算法中的VSCLMS算法。
2.2 NVSCLMS算法的提出及性能分析
本文遵循这一思想提出一种新型变步长CLMS算法(文中称为NVSCLMS算法)。将带有块步长思想的基于Sigmoid函数的变步长LMS算法引入CLMS算法。变步长LMS算法迭代步长为:
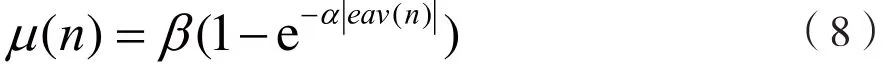
其中eav(n)是根据文献[4]提及的块步长思想而设计的误差平均量,更新公式如下:

与其他变步长LMS算法相同,新算法必须满足α>0,0<β<μmax的收敛条件。
NVSCLMS算法的性能分析可以从以下两方面展开。
第一,对于CLMS算法的性能分析,文献[2]和文献[3]进行了详细阐述。VSCLMS算法作为CLMS算法的延伸,具有类似CLMS算法的性能。
对于NVSCLMS算法,其变步长迭代规则为:

当n→∞时,理想状态下步长会收敛为一个很小的值,可取如下近似:此时,交叉EMSE表达式如下:

由于,且μ<μ<μ,
2120得出结论Jex,2<Jex,12<Jex,1。符合文献[2]中三种假设的第二种假设,因此整个NVSCLMS算法的稳态误差Jex(∞)≈Jex,2(∞)。所以,该NVSCLMS算法拥有变步长LMS算法的收敛速度,同时能够达到理想的稳态误差。
第二,将NVSCLMS算法中引入块步长思想的变步长LMS算法(文本称为NVSLMS算法)与固定步长LMS算法、文献[5]中VSCLMS算法提及的变步长LMS算法(本文称为VSLMS算法)进行仿真比较。
将3种算法在同一系统辨识模型中进行仿真实验:在信噪比为20 dB的情况下,假设未知系统为8阶横向滤波器,抽头系数Hn=[0.878 3,-0.580 6,0.653 7,-0.322 3,0.657 7,-0.058 2,0.289 5,-0.271 0]。当更新至600次时发生突变,抽头系数Hn=[0.653 7,-0.322 3,0.657 7,-0.058 2,0.289 5,-0.271 0,0.127 8,-0.150 8],再进行600步更新。固定步长LMS算法的参数:μ=0.01。VSLMS算法和NVSLMS算法的参数均为β=0.08,α=0.8。学习曲线如图2所示。

图2 三种LMS算法学习曲线比较
通过以上单一LMS滤波器的仿真对比可以发现,在不改变稳态误差的前提下,NVSLMS算法无论是在收敛速度还是跟踪性能方面,都相对于固定步长LMS算法和文献[5]中提到的VSLMS算法有较大程度的提高。因此,将NVSLMS算法引入CLMS,将会有效改善CLMS算法和文献[5]提出VSCLMS算法所出现的不足。
3 NVSCLMS算法在系统辨识系统中的应用分析
所谓系统辨识就是根据系统的输入和输出信号,建立系统模型的理论和方法。当给定一个未知的系统时,自适应滤波器通过各种算法逼近这个系统;当系统达到稳态时,自适应滤波器的权系数即是未知系统的系数,从而达到系统辨识的目的。
为了进一步验证本文提出算法与其他算法相比具有良好的性能,现在系统辨识的应用中,将本文提出算法同CLMS算法、文献[5]提出的VSCLSM算法进行比较。在信噪比为20 dB的情况下,假设未知系统为8阶横向滤波器,抽头系数Hn=[0.878 3,-0.580 6,0.653 7,-0.322 3,0.657 7,-0.058 2,0.289 5,-0.271 0];当更新至600次时发生突变,抽头系数Hn=[0.653 7,-0.322 3,0.657 7,-0.058 2,0.289 5,-0.271 0,0.127 8,-0.150 8],再进行600步更新。每种算法进行200次独立仿真,求取统计平均值进行比较。同时,为能客观比较系统性能,各种算法均取其他文献中讨论过的相对最优参数。CLMS算法中,μ1=0.08,μ2=0.01,μa=200;文献[5]提出的VSCLMS算法中,β=0.08,α=0.8,μ2=0.01,μa=200;本文提出算法同样取,β=0.08,α=0.8,μ2=0.01,μa=200。于是,得出对比学习曲线如图3所示。

图3 NVSCLMS算法与其他算法对比学习曲线比较
由图3可以得出,在NVSCLMS算法中,快速滤波器步长上限取0.08(CLMS算法中快速滤波器步长)的情况下,与CLMS算法比较,收敛速度方面并没有明显差距,但在均方误差上有显著提高。此时,若改变快速滤波器收敛上限,必将获得比CLMS算法更快的收敛速度。因此,NVSCLMS算法与CLMS算法相比,收敛速度、稳态误差和跟踪性能三个方面都有很大提高。与文献[5]中提出的VSCLMS算法相比较,在稳态误差基本相同的情况下,NVSCLMS算法在收敛速度和跟踪性能有大幅度提升。
4 结 语
NVSCLMS算法在不改变原有CLMS算法的基础上,将带有块步长思想的变步长LMS算法带入CLMS算法中替代原有的快速收敛LMS算法,使得CLMS算法能够根据收敛进程及环境变化的要求随时调整步长,增强了滤波器的灵活性和实用性。通过理论分析和仿真实验,将NVSCLMS算法与VSCLMS算法和固定步长CLMS算法相比较发现,NVSCLMS算法不仅有较快的收敛速度,还降低了稳态误差,在跟踪性能上也明显优于已提出的变步长凸组合算法。可见,本文提出的NVSCLMS算法在收敛速度和稳态误差之间找到了一个新的调和点,从而促使滤波器取得了更好的滤波效果。
[1] Widrow B,Mccool J M,Arimoer M G.Stationary and NonStationary Learning Characteristics of the LMS Adaptive Filter[J].Proceedings of the IEEE,1976,64(08):1151-1162.
[2] Arenas-Garcia J,Figueiras-Vidal A R,Sayed A H.Steady State Performance of Convex Combinations of Adaptive Filters[C].Proceedings of IEEE International Conference Acoustics,Speech,and Signal Processing,2005:33-36.
[3] Arenas-Garcia J,Figueiras-Vidal A R,Sayed A H.Meansquare Performance of a Convex Combination of Two Adaptive Filters[J].IEEE Signal Processing,2006,54(03):1078-1090.
[4] 张炳婷,赵建平,马淑丽.新的变步长LMS算法在系统辨识中的应用[J].通信技术,2015,48(06):653-656.
ZHANG Bing-ting,ZHAO JIAN-ping,MA Shuli.Application of Novel Variable Step Size LMS Algorithm in System Identification[J].Communication Technology,2015,48(06):653-656.
[5] 于霞,刘建昌,李鸿儒.一种变步长凸组合自适应滤波器及其均方性能分析[J].电子学报,2010,38(02):480-484.YU Xia,LIU Jian-chang,LI Hong-ru.A Convex Combination of Variable Step-size Adaptive Filter and Its Mean-Square Performance Analysis[J].ACTC ELECTRONICA SINICA,2010,38(02):480-484.
[6] 曾乐雅,许华,王天睿.基于洛伦兹函数的变步长凸组合最小均方算法[J].系统工程与电子技术,2016,38(05):998-1003. ZENG Le-ya,XU Hua,WANG Tian-rui.Low Computational Complexity Variable Step-size CLMS Algorithm based on Lorentzian Function[J].Systems Engineering and Electronics,2016,38(05):998-1003.
[7] 陈立伟,谭志良,崔立东.基于双曲正切函数的变步长凸组合最小均方误差算法[J].装甲兵工程学院学报,2015,29(05):94-96.
CHEN Li-wei,TAN Zhi-liang,CUI Li-dong.A Convex Combination of Variable Step LMS Algorithm based on Hyperbolic Tangent Function[J].Journal of Acadamy of Armored Force Engineering,2015,29(05):94-96.

王 蒙(1990—),男,硕士研究生,主要研究方向为无线通信技术;
赵建平(1964—),男,学士,教授,主要研究方向为无线通信技术;
杨恒耀(1990—),男,硕士研究生,主要研究方向为无线通信技术。
Variable Step-size Convex-combination Adaptive Algorithm and Its Performance Analysis
WANG Meng, ZHAO Jian-ping, YANG Heng-yao
(College of Physics Engineering, Qufu Normal University, Qufu Shandong 273165, China)
For further solving the contradiction of between the convergence speed and the steady-state error, and for improving the performance of adaptive filtering algorithm, the variable step size algorithm is introduced into the convex-combination adaptive filtering algorithm (CLMS), and thus a new variable step-size convex-combination least-mean-square (VSCLMS) algorithm is proposed. The algorithm, with a variable step size algorithm based on block step size, replaces the fast convergence algorithm in the original CLMS algorithm. Theoretical derivation and simulation analysis indicate that the proposed algorithm could improve the flexibility and practicability of the CLMS algorithm, and exhibits much better filtering effect than other variable step size algorithms, CLMS algorithm and proposed VSCLMS algorithm in the three aspects of convergence speed, steady state error and tracking performance.
adaptive filtering; CLMS; variable step-size algorithm; block step-size; NVSCLMS
0 引 言
最小均方误差(LMS)算法是Windrow和Hoff在1960年提出的一种建立在维纳滤波理论上的算法。它以最小均方误差为准则,通过最速下降法来获得最优维纳解[1]。它的主要过程是通过调节自适应滤波器的权系数,使滤波器输出信号与期望信号之间误差的均方最小。由于LMS算法计算量小、鲁棒性高、结构简单、便于实现和控制等优点,被广泛应用在通信领域的回波消除、信道自适应均衡、噪声中信号追踪、系统模型识别等方面。步长选择在LMS算法中起着十分重要的作用:大步长意味着快速收敛,但带来了较大的稳态误差;小步长可以满足较小的稳态误差,但是严重影响收敛速度。因此,现有的固定步长LMS很难同时获得较快的收敛速度及较低的稳态误差。为了解决两者的矛盾,许多变步长LMS算法先后被提出,其中比较具有代表性的算法有改进的Sigmoid函数变步长LMS算法(SVSLMS)、归一化最小均方误差算法(NLMS)、指数因子变步长算法等。它们遵循的原理:在算法收敛初期选择较大的步长以获得较快的收敛速度,当进入收敛稳态阶段,选用较小的步长来获得较低的稳态误差。变步长LMS算法虽然通过对算法步长的控制使收敛速度和稳态误差基本都能满足实际应用的要求,但其对两种性能都有些许折中,在一定程度上限制了自适应滤波的性能。
National Natural Science Foundation of China(No.11404185);Supported by the science and technology projectof higher education of Shandong province(No.J12LN08);Qufu Normal University technology development project(No.hxkj2015017)
TN713
A
1002-0802(2016)-10-1301-05
10.3969/j.issn.1002-0802.2016.10.007
2016-06-08;
2016-09-23
data:2016-06-08;Revised data:2016-09-23
国家自然科学基金资助项目(No.11404185);山东省高等学校科技计划项目资助(No.J12LN08);曲阜师范大学技术开发项目(No.hxkj2015017)

