五自由度串并联机构的运动学分析*



五自由度串并联机构的运动学分析*

提出了一种五自由度串并联机构，并对其作了正反解分析。利用杆长不变，采用矢量几何方法，求得了机构的位置反解。基于反解方程，利用数值迭代的方法，求机构并联部分的位置正解，再利用几何投影的办法，进一步求出了机构串联部分的位置正解，并通过实例对所推导出的正反解算法进行了验证，证明其是正确有效的。

串并联机构；位置正反解；数值迭代

机构运动位置分析包括位置反解和位置正解，是受力分析、误差分析、工作空间分析和运动控制的基础。串并联机构运动学正反解分析包括串联部分正反解和并联部分正反解。其中，并联部分比串联部分较为容易求解，而并联部分反解比正解更容易求解。

目前，求解位置正解主要有数值解法和封闭解法[1]。高建设等[2]以能耗最小姿态为最优姿态,基于矢量法求解了该串并混联腿的运动学正解和反解。韩方元等[3]提出了一种求解3-PRS并联机构正解的快速数值解法，使得计算速度比普通算法快1.5倍。毕树生等[4]提出了一种新颖的用于微动操作的串并联机构，利用矢量运算的方法分析了机构的位置正反解。刘晶晶等[5]设计了一种串并混联7-DOF仿人机械臂,并通过对并联机构进行运动学分析和D-H建模,建立了仿人机械臂正运动学的数学模型。蒋俊香[6]提出了新一代串并联机床LINKS-EXE700，并对其反解作了详细的介绍，先利用姿态矩阵求解串联部分的反解，然后利用杆长不变建立约束方程，求解并联部分的反解。纪校娟[7]对Tripod机构进行了运动学分析，采用简洁的数值搜索方法进行求解，省去了方程求解的繁琐过程。

本文对五自由度串并联机构分别进行串联部分和并联部分的正反解位置分析，并通过MATLAB软件进行正反解验算，证明了算法的科学性和可靠性。

1 五自由度串并联机构的机构描述

五自由度串并联机构(见图1)是由并联部分和串联部分构成混联机构，并联部分由定平台、动平台和3个分支组成。3个分支是一个平行四边形长杆，一端与滑块导轨连接，另一端与动平台连接，这样就保证了动平台始终与定平台平行，滑块由电动机带动丝杠传动，两自由度串联机构由2个转动副构成。机构简图如图2所示。

图1 五自由度串并联机构

图2 五自由度串并联机构的结构简图

2 五自由度串并联机构的正反解研究

2.1 五自由度串并联机构的反解

2.1.1 串联部分的反解

已知刀具的位置和姿态，求解动平台中心的位置和串联部分的转角，这个过程称为串联部分的反解。串联部分机构图如图3所示，其包含2个转动副。刀具运动到空间某一位姿的状态示意图如图4所示。在刀头点建立坐标系O2X2Y2Z2，旋转副1的长度为l1，旋转副2(含刀具)的长度为l2，此时刀具转动副R1和R2均有转动角度。

图3 串联部分机构图 图4 串联部分状态示意图

(1)

(2)

(3)

串联部分转动副转角求解过程如下：

(4)

(5)

2.1.2 并联部分的反解

利用串联部分求取的动平台的位置，求并联部分3个滑块的位置，是并联部分的反解。利用坐标变换，可以计算出动平台各铰点在定系中的坐标(B1,B2,B3)，然后根据杆长不变，得出定平台各个铰点的坐标，最后求出3个滑块的位移(h1,h2,h3)。

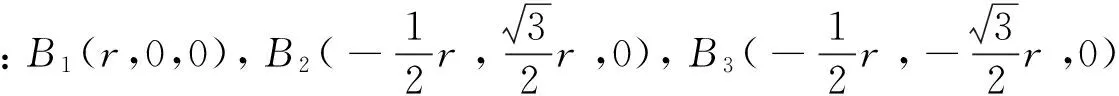
(6)

将机构的结构参数和动平台的位置参数带入式6，分别计算出h1,h2,h3。

由：L2=(R-xO1-r)2+(yO1)2+(h1-zO1)2

(7)

由：

则：

(8)

由：

则：

(9)

2.2 五自由度串并联机构的正解

机构的位置正解方法是已知机构的并联部分滑块的位置和串联部分转动副的转角，求解刀具刀头点的位置和姿态。利用微分求导法可以求出机构并联部分的雅可比矩阵，然后将反解方程等式两侧同时对时间t求一阶偏导，可得到：

(10)

对上式，令：

则J就是机构并联部分的输入参数与输出参数之间的3×3阶雅可比矩阵。

2.2.1 并联部分的正解

近年来，串并联机构已经成为机器人技术研究的热点。与单纯的串联机构或并联机构相比较，串并联机构兼顾了并联和串联的优势，其既具有并联机构的刚度大、响应快的优势，也拥有串联机构工作并联部分的正解流程图如图5所示。

图5 并联部分的正解流程图

2.2.2 串联部分的正解

如图6所示为刀具在XY平面内的投影。通过几何计算即可获得刀具到头点位置相对于动系原点O1的坐标。

(11)

(12)

(13)

(14)

从而，可以计算出刀具到头点C在定系中的位置坐标：

(15)

要求刀具的姿态，可以先求出刀具轴线向量，然后再计算单位向量。

(16)

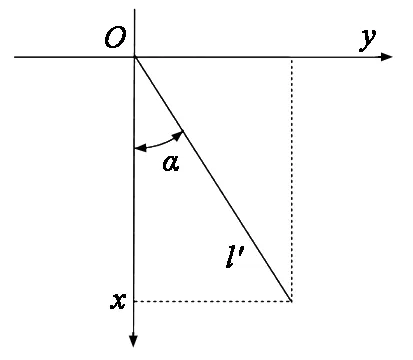
图6 刀具在XY平面内的投影

3 位置正反解算例

下述通过实例来验证上述正反解计算过程的正确性。设定机构的结构参数为：L= 750mm，R= 750mm,r=350mm,l1=300mm, l2=300mm。反解计算，给定输入值，刀具在定坐标系中的位姿参数为U0(27 100，-1 300，0.469 8，0.813 8，-0.342 0)，利用MATLAB反解，得出3个滑块的位置(h1, h2, h3)为：(-370.539 8，-336.629 0，-180.328 7)，串联部分转动副转角(α,β)为(30°,20°)。正解验证，将反解得出的结果带入正解算法，得出刀具在定系中为位姿参数为U0(27 100，-1 300，0.469 8，0.813 8，-0.342 0)。经比较，正好是刀具的已知位姿，由此正反解算法得到了相互验证。

4 结语

提出了一种五自由度串并联机构，并对其作了正反解分析。并联部分正解采用数值迭代进行搜索计算，既保证了运算速度，也使得计算准确无误；串联部分反解采用空间向量的计算，方法简便、快捷，并通过将反解结果作为正解条件，验证了正反解的正确性。

[1] 黄真，赵永生，赵铁石.高等空间机构学[M].北京：高等教育出版社，2006.

[2] 高建设, 李明祥, 侯伯杰,等. 新型四足步行机器人串并混联腿的运动学分析[J]. 光学精密工程, 2015, 23(11):3147-3160.

[3] 韩方元，赵丁选，李天宇.3-RPS并联机构正解快速数值算法[J].农业机械学报, 2011, 42(4):229-233.

[4] 毕树生, 王守杰, 宗光华. 串并联微动机构的运动学分析[J]. 机器人, 1997(4):259-264.

[5] 刘晶晶, 彭俊泉, 刘新华. 基于MATLAB的串并混联7-DOF仿人机械臂正运动学分析及仿真[J]. 机械传动, 2015(7)：59-62，66.

[6] 蒋俊香. 新一代串并联机床LINKS-EXE700工作机制分析[J]. 机床与液压, 2013(19):70-72.

[7] 纪校娟.Tripod机构的运动学和静力学分析[D]. 哈尔滨：哈尔滨工业大学, 2008.

责任编辑 马彤

肖 飞，伞红军，赵俊杰，雷俊松

(昆明理工大学 机电工程学院，云南 昆明 650500)

Kinematic Analysis of Five-DOF Parallel and Serial Mechanism

XIAO Fei， SAN Hongjun， ZHAO Junjie， LEI Junsong

(Faculty of Mechanical and Electrical Engineering, Kunming University of Science and Technology, Kunming 650500, China)

The five-DOF serial parallel mechanism is proposed and the forward and inverse solutions are analyzed. The analysis of the positive and negative solutions is made. The inverse solution of the mechanism is obtained by using the vector geometry method. Based on the inverse solution equation, using the numerical iterative method, the position of the parallel part of the mechanism is obtained, and then the geometric projection method is used to prove the position of the series part of the mechanism. Finally, the positive and negative solution algorithm is verified by an example, which proves that the algorithm is correct and effective.

serial-parallel mechanism， forward and inverse solutions of position， numerical iterative

yO1=yO2-l1py

zO1=zO2-l1pz+l2

L=‖A1-B1‖，L=‖A2-B2‖，L=‖A3-B3‖

h2=zO1+

h3=zO1+

l′=lsinβ

ax=l′cosα

ay=l′sinα

C=O1+O2

肖飞(1987-)，男，硕士研究生，主要从事并联机器人等方面的研究。

2016-04-13

* 湖南科技大学机械设备健康维护重点实验室开放基金项目(201403)

TP 242.2

A