基于粒子群算法的动力升档换档品质优化控制

李兴忠　宋　斌　童燕华　陈钰尘　付　尧

(1. 杭州前进齿轮箱集团股份有限公司，杭州 311203；2. 吉林大学汽车仿真与控制国家重点实验室，长春 130022)



基于粒子群算法的动力升档换档品质优化控制

李兴忠1,2宋斌1童燕华1陈钰尘1付尧2

(1. 杭州前进齿轮箱集团股份有限公司，杭州 311203；2. 吉林大学汽车仿真与控制国家重点实验室，长春 130022)

通过分析动力换档过程离合器切换时序控制不当对换档品质产生影响的问题，针对该问题采用粒子群优化算法，以理想换档过程的换档品质客观评价模型为基础构建适应度函数，提出了动力升档过程的控制量最优化控制策略，仿真结果表明了该控制策略在提高升档过程的换档品质方面效果明显。

动力换档换档品质适应度函数控制策略粒子群算法

0　引言

动力换档过程离合器切换时序控制是换档过程控制的关键技术，同时也是难点之一[1]。自动变速器的换档过程可以分为动力换档和非动力换档，关于换档过程控制的研究一直是国内外学者关注的重点。文献[2]采用反馈及前馈控制方法实现换档过程离合器控制，进一步提高了控制精度。文献[3]对车辆动力换档的过程及换档品质控制原理进行了较为深入的分析。文献[4]提出了基于减小离合器实际换档中的换档冲击和滑摩功，通过数字比例溢流阀调整离合器油缸内的压力来控制档位离合器和方向离合器的结合顺序实现动力换档。文献[5]提出了基于转矩的升档过程惯性相发动机协调控制策略，有效降低了惯性相输出扭矩波动，但并未给出扭矩相的控制方法。

本文建立了某自动变速器的离合器-离合器换档过程动态模型，在仿真分析的基础上分析了离合器切换时序控制与换档品质之间紧密相关，并且以动力升档换档过程控制品质作为优化目标，设计了基于粒子群优化算法的换档过程控制策略进行控制量寻优，通过仿真进行了对比验证，为相关控制系统的研究提供了参考。

1　动力升档过程建模及仿真分析

动力换档过程离合器切换时序合适与否会直接影响换档品质，下面以动力升档过程为例，分析离合器切换过程及其影响因素。为了得到比较合理的仿真分析结果，采用动态仿真模型进行验证。

1.1动力升档过程建模

依据离合器-离合器换档原理建立的动力换档等效模型如图1所示。

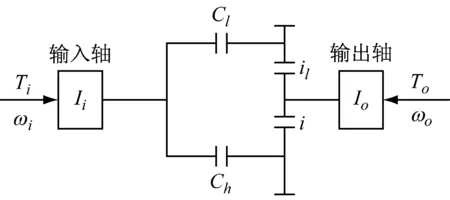
图1　离合器-离合器动力换档等效模型

对于输入轴其平衡方程为：

(1)

其中，Ti为发动机输出扭矩，Ii为与输入轴连接构件等效到输出轴上的转动惯量，ωi为变速器输入轴转速。

对于输出轴则有：

(2)

式中，il、ih分别为变速器低、高档位传动比，To为变速器输出扭矩，Io为与变速器输出轴连接构件等效到输出轴上的转动惯量，ωo为变速器输出轴转速。

低档位离合器主从动盘转速差为：

(3)

(4)

离合器所能传递的扭矩可表示为：

(5)

式中，Tc为离合器传递扭矩，μ为摩擦系数，r为有效摩擦半径，n为摩擦面数，A为离合器液压缸工作活塞有效面积，P为离合器工作油压，Fs为离合器回位弹簧拉力。

则低、高档离合器所传递的扭矩由式(5)可得，分别为：

(6)

(7)

1.2仿真分析

在所搭建的动力换档仿真模型中，以发动机的输出扭矩Ti、低/高档离合器扭矩容量Tpl、Tph作为控制量，分别针对离合器结合时出现的过早或过迟情况进行仿真，其结果分别如图2和图3所示。

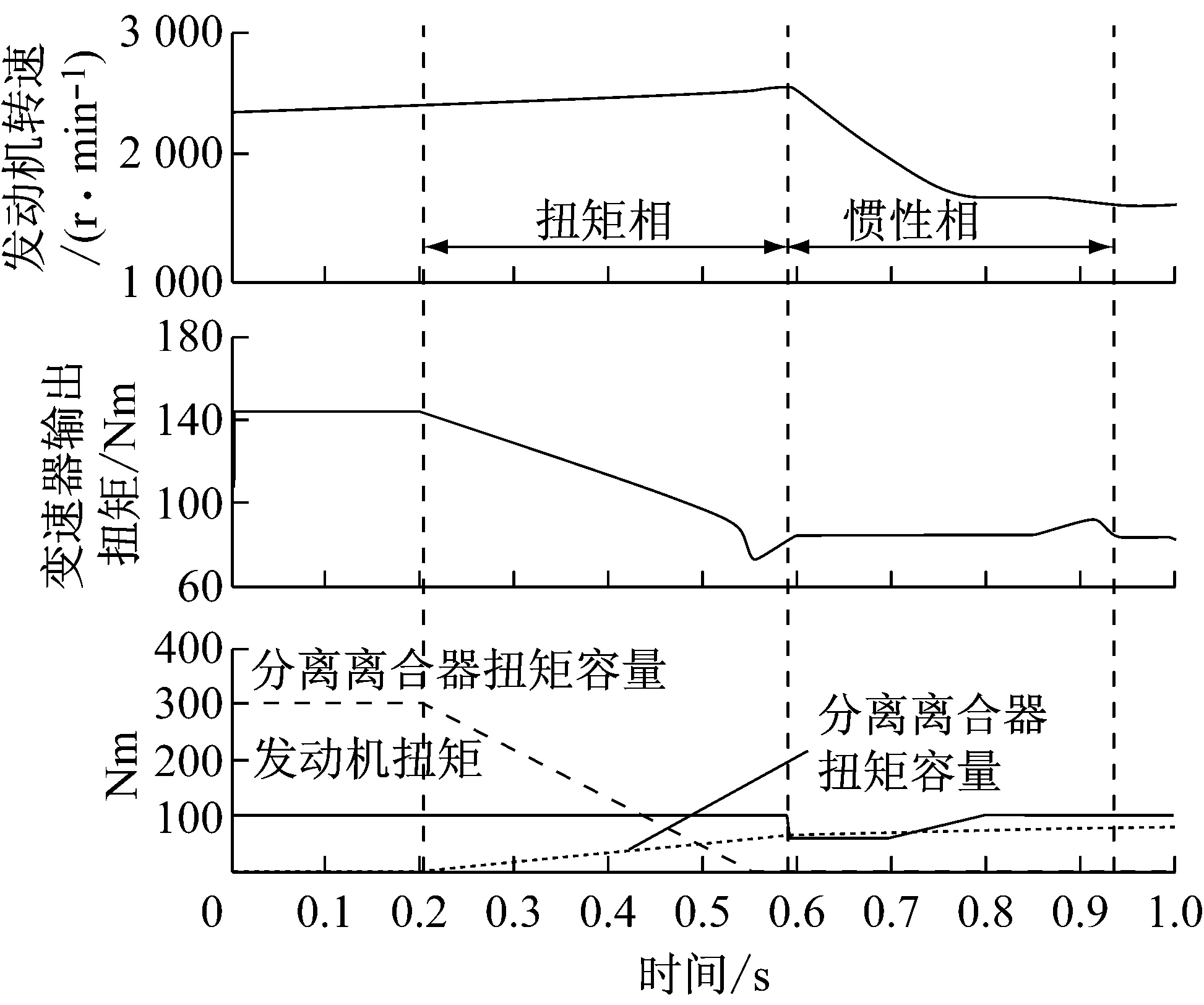
图2　低档离合器过早分离仿真结果

综合图2和图3可见，如果待分离离合器出现过早分离的情况会引起离合器的滑摩，严重会导致发动机的飞车，造成不必要的功率损失，最终结果会导致变速器输出扭矩降低，换档品质恶化。分离过迟则会导致分离离合器产生负扭矩，引起功率循环[6]，同样会导致变速器输出扭矩的进一步下降，严重影响换档舒适性。

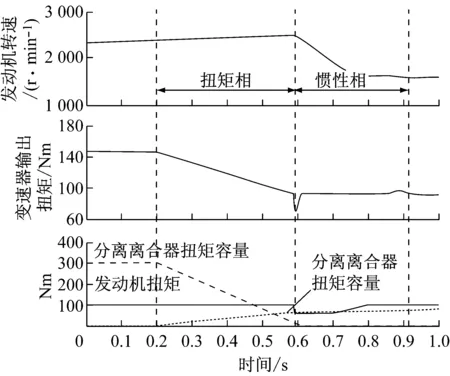
图3　低档离合器分离过迟仿真结果

从上面的分析结果可以推断，离合器切换时序控制与换档品质紧密相关，切换时序控制策略设计不合理会导致换档品质恶化，如何保证离合器最佳切换时序是换档过程综合控制策略着重解决的问题。

2　基于粒子群算法的换档品质优化

2.1粒子群优化算法

粒子群优化算法(Particle Swarm Optimization，PSO)由Kennedy和Eberhart于1995年提出的一种基于群智能的演化计算技术[7]，源于复杂适应系统，是一种高效的并行搜索算法。

由m个粒子组成的粒子群在D维搜索空间中以一定的速度飞行，粒子在搜索时，考虑到其历史最优点及全局最优点，进行搜索位置变换。则第i个粒子的位置表示为：

(8)

其速度为：

(9)

个体最优位置为：

(10)

种群的全局最优位置为：

(11)

则粒子的位置和速度按照方程(12)进行变化：

(12)

(13)

式中，c1和c2为学习因子，r1、r2为两个随机数，其取值范围为(0,1)，其作用是增加搜索的随机性。粒子的速度范围为[vmin,vmax]，为了得到合理的算法收敛性，在式(12)中引入惯性权重w，则原式变为：

(14)

惯性权重在本文中是一个非负数，其功能主要是调节解空间的搜索范围。若使惯性权重在迭代计算中呈递减趋势，优化算法在开始时具有较好的全局寻优性能，在后期具有较好的局部搜索能力。惯性权重的递减一般遵循下述方程：

(15)

式中，wst、wed分别为初始惯性权重和终止惯性权重，tmax表示最大迭代次数，t表示当前迭代次数。PSO算法的一般迭代流程如图4所示。

2.2动力升档过程控制量寻优

本文以基于理想换档过程的换档品质客观评价模型[7]为基础构建适应度函数，针对升档控制量中的主要参数(扭矩相接合离合器油压变化率Δp、惯性相发动机降扭目标量Tred)进行优化，采用粒子群优化算法[8-11]对动力升档过程的控制量进行寻优，并以趋近度Ei作为适应度函数：

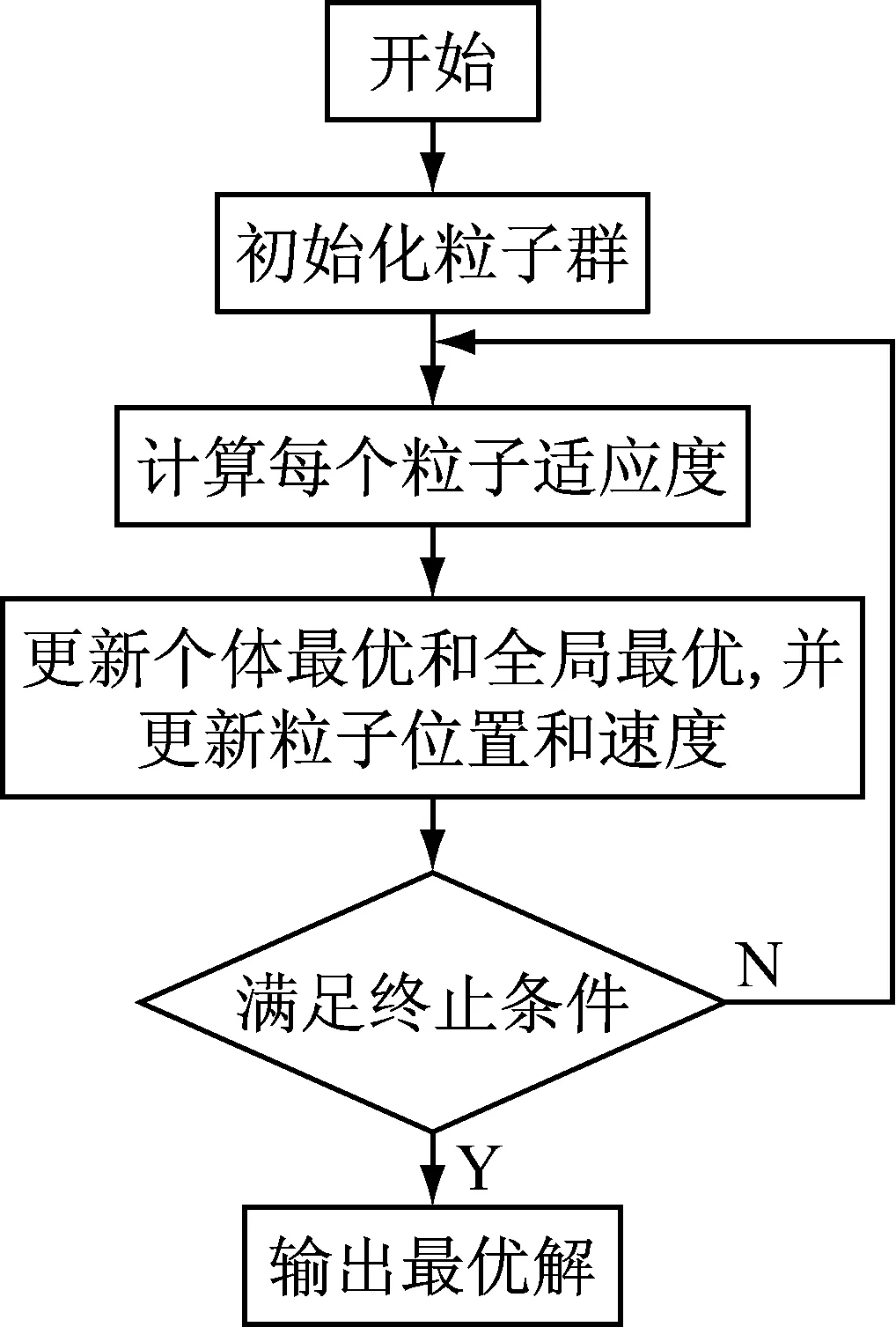
图4　PSO算法迭代流程

式中，E(Xi)为对应粒子的趋近度，Xi=[Δpi，Ti_red]为粒子，其中二维元素分别为接合离合器压力变化率和发动机降扭目标量。约束条件中，pmax、Tmax分别为优化量上限，同时也需考虑发动机转速上限ωmax。因此，运用粒子群算法进行升档控制量寻优的过程就转化为求趋近度函数最大值过程。基于PSO算法的控制量寻优过程如图5所示

maxZ=E(Xi)

(16)

图5　控制量寻优过程

在控制量寻优的过程中，粒子群算法中位置和速度的更新操作采用式(17)的方式：

(17)

在Matlab/simulink软件中搭建基于PSO算法的控制策略仿真模型，并且以PSO算法的输入作为粒子的适应度值，该值为基于理想换档过程换档品质评价模型的输出，设置PSO算法的主要参数进行仿真分析。

3　优化结果

为了说明优化后的结果，本文以升档过程的控制量寻优为优化过程，在油门开度区间[0-100%]内，设置步长为20%油门开度，进行参数优化，优化后的结果如图6、图7所示。

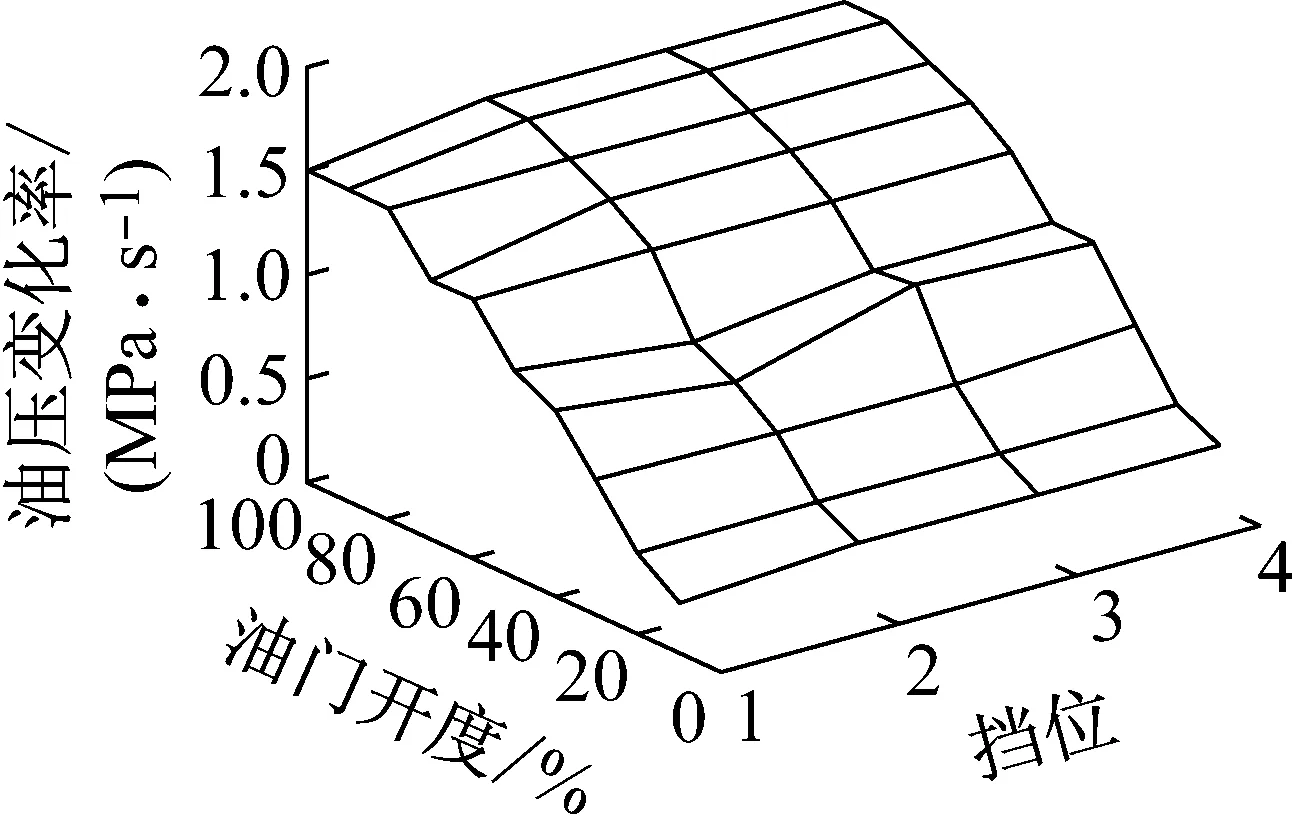
图6　优化后离合器油压变化率

图7　优化后发动机降扭变

由图6可知，离合器油压变化率与油门开度是一个非线性的关系，且随着油门开度的升高而增大，油门开度较低时，油压变化率随之减小。同样，从图7中可知，发动机降扭目标量最大值约为30Nm，随着档位升高，换档过程中发动机降扭目标量也随之减小。优化得到的MAP图可根据需要，直接用于实际换档过程控制。

表1是升档控制策略在采用PSO算法优化前后相应指标变化情况。

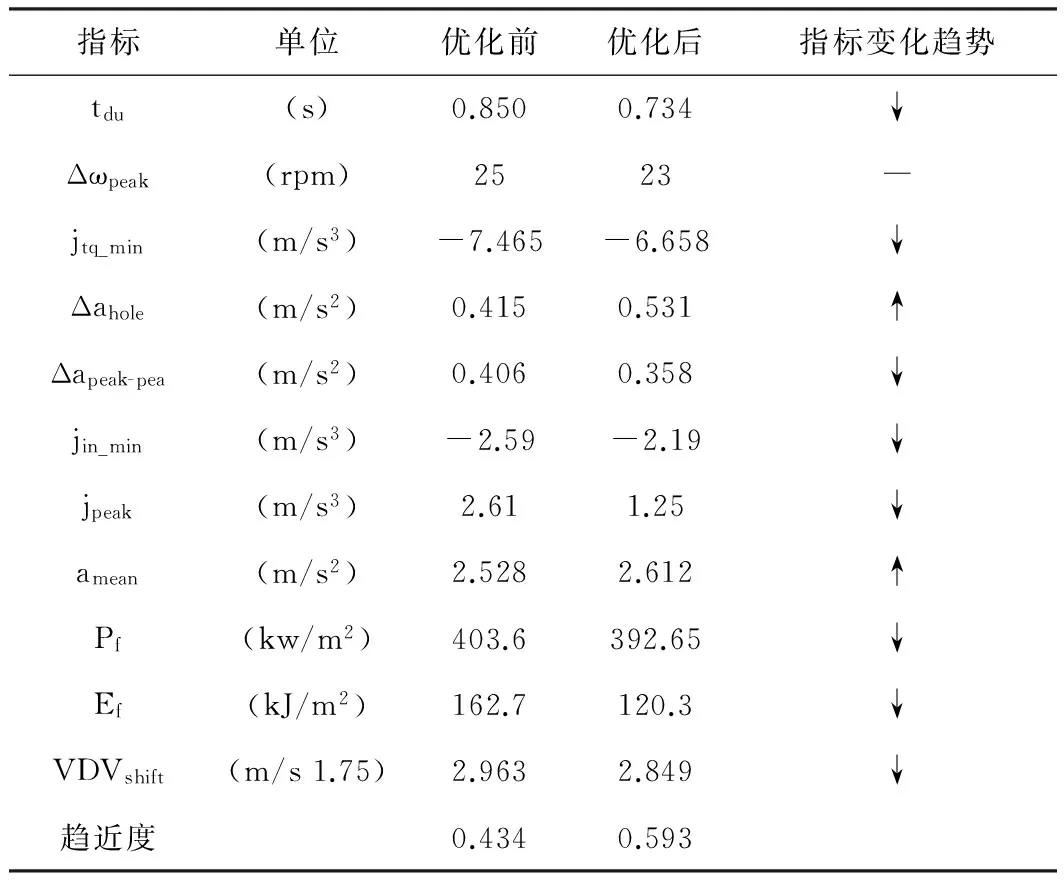
表1　优化前后评价指标对比

从表1(指标参数意义见附件)中仿真数据可明显看出，优化后的换档持续时间较原来缩短了约0.116 s，其它关键指标换档过程平均加速度、离合器能量密度等都有明显改善，而在发动机转速超调量上基本维持原有状态。总体趋近度值与原来值相比有明显的提升。

图8中的仿真曲线是在同工况下得到的PSO算法优化前、后换档控制结果。利用数据采集设备对动力升档过程中的发动机转速、离合器压力、发动机扭矩、车辆纵向加速度和冲击度信号的变化情况实现了实时监控和数据采集。图8中可以看出，当油门开度为100%时，动力换档过程的开始时间位于3.5 s处，随着要接合离合器缸内作用压力的增大，滑摩转速控制器通过控制分离离合器压力使发动机的滑摩速差保持在20 rpm左右，通过换档品质客观评价系统中提取的相关评价指标可以看出，指标Δωpeak在优化前后的变化并不明显，进一步说明采用了滑摩转速控制器能较好地抑制扭矩相发动机转速超调。在惯性相结合离合器压力保持了恒定。由加速度及冲击度变化曲线可知，优化后的换档过程较平顺，接合离合器压力变化率Δp经优化后，其值由0.8 Mpa/s变为1.2 Mpa/s。综上可知，采用优化控制策略后，动力换档相关指标得到了明显改善。

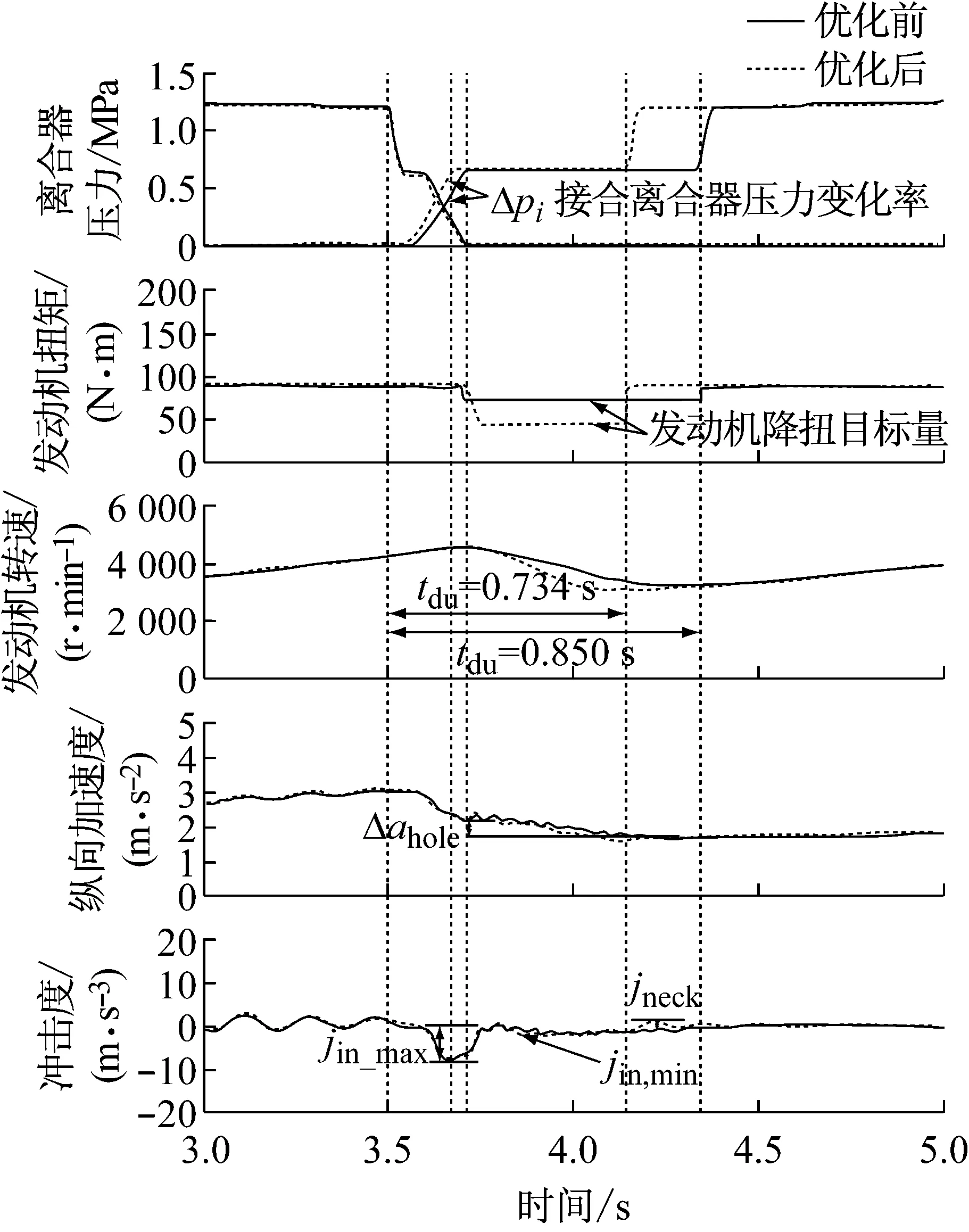
图8　优化前后动力升档仿真曲线

4　结论

本文建立了离合器—离合器式动力换档变速箱仿真模型，对动力升档过程进行了仿真分析。通过对仿真结果的分析，可知离合器切换时序是影响换档品质的主要因素，该因素在系统中也是最难实现控制的。在此基础上，提出了基于粒子群算法的动力升档换档品质优化控制策略，以理想换档过程的换档品质客观评价模型为基础构建了适应度函数，对目标参数扭矩相接合离合器油压变化率和惯性相发动机降扭目标量进行了控制量寻优，并对设计的控制策略进行了仿真验证，仿真结果验证了控制策略的有效性，换档品质得到了有效提升。

附件：

tdu—换档持续时间；

Δωpeak—扭矩相发动机转速超调；

jtq_min—扭矩相冲击度最小值；

Δahole—扭矩相纵向加速度最小值与目标差值；

Δapeak-peak—纵向加速度峰峰值；

jin_min—惯性相冲击度最小值；

jpeak—惯性相冲击度最大值；

amean—纵向加速度算术平均值；

pf—离合器功率密度；

Ef—离合器能量密度；

VDVshift—纵向冲击剂量值。

[1]M.Goetz, M.C.Levesley, D.A.Crolla.双离合器变速箱换档动力学和控制[J].传动技术,2006,20(3):37-47.

[2]孙贤安,吴光强.双离合器式自动变速器汽车换档控制策略仿真[J].东南大学学报,2011,41(4):729-733.

[3]李闪.车辆动力换档与换档品质控制分析[J].科学之友，2008，(17).

[4]赵国奇,李华,姚进.重型车辆动力换档过程离合器结合动作时序控制[J].中国西部科技，2012,6.

[5]万国强,黄英,张付军等.自动变速器升档过程惯性相发动机协调控制[J].机械工程学报,2012,48(16):91-96.

[6]秦大同,刘永刚,胡建军等.双离合器式自动变速器两离合器起步控制与仿真[J].机械工程学报,2010,46(18):122-127.

[7]Fu, Y., Lei, Y., Shaohua, S., Zeng, H. et al., “Shift Quality Evaluation of DCT Based on TOPSIS Model,”SAE Technical Paper 2014-01-1166,doi:10.4271/2014-01-1166.

[8]张松,吴光强,郑松林.基于元胞粒子群算法的干式DCT换档品质优化[J].汽车工程,2011,33(9):809-813.

[9]秦大同,刘永刚,胡建军等.双离合器式自动变速器两离合器起步控制与仿真[J].机械工程学报,2010,46(18):122-127.

[10]顾强,程秀成.基于粒子群算法的电动汽车DCT升档动力协调控制[J].农业工程学报,2012,28(8):84-91.

[11]段晓东,王存睿,刘向东.粒子群算法及其应用[M].辽宁大学出版社,2007.

Optimization Control of Power-On Shifting Quality Based on PSO Algorithm

SongBin1LiXingzhong1,2TongYanhua1ChenYuchen2FuYao1

(1.HangzhouAdvanceGearboxGroupCo.,Ltd.,Hangzhou311203;2.StateKeyLaboratoryofautomotivesimulationandControl,JilinUniversity，Changchun130022)

Through analyzing the process of power-on shifting based on the dynamic model of clutch to clutch, the main factors affecting shift quality is the improper switch sequential control of clutches. An new algorithm is proposed on the basis of the Particle Swarm Optimization (PSO) algorithm according to this problem. An optimization control strategy is proposed for power-on upshift, which building a fitting function based on the shift quality evaluation model during perfect shifting process. The simulation results show that the application of the optimized control strategy had obvious effect on improving the shift quality during the power-on shifting.

Power-on shiftingShifting qualityFitting functionControl StrategyPSO Algorithm

1006-8244(2016)01-009-05

浙江省博士后科研项目择优资助项目(BSH1502066)

李兴忠，

U463.212

B