从借题发挥到解决问题

卜以楼

从借题发挥到解决问题

卜以楼

一、背景分析

在一次校本课程活动中，笔者根据“苏科版”义务教育教科书《数学》八年级中的两道原题，设计了下列问题，供学生探究。

八年级（上）和八年级（下）的课本中分别有这样两道习题：

（1）如图1，△ABC和△CDE都是等边三角形，且点A、C、E在同一直线上，试说明AD与BE的关系，并说明理由。（八上第67页）

（2）如图2，四边形ACDE和CBGF都是正方形，且点A、C、B在同一直线上，试说明AF与BD的关系，并说明理由。（八下第94页）

请你根据上述两道习题的数学本质，借题发挥，提出一个关于这两个问题本质的新问题，并给予解答。

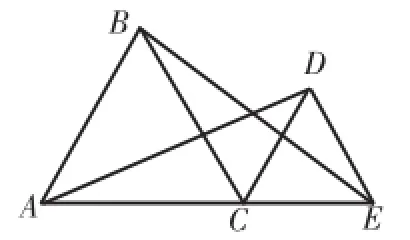
图1

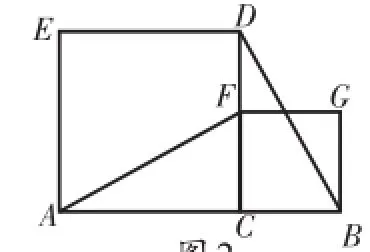
图2

这是一道开放题，尽管可以从多角度发现不同的问题，提出不同的问题，但是能够理解题意，揭示这两个问题本质，从正三边形（等边三角形）到正四边形（正方形）再到正n边形去探索类似于问题（1）、问题（2）中的两条线段关系的学生却寥寥无几。究其原因，是学生平时对问题的解决只止于习题本身，自认为只要将提供的习题做出个正确答案，就算是解决问题了。其实这种“学答”式解决问题的思维方法，没有在真正意义上去解决问题。它不能算是一种有效的、高质量的思维方式，它缺少对问题的本质研究，缺少对问题的多维迁移，只能算是“一题一答”。那么，什么样的活动才是真正意义上的解决问题呢？笔者认为，在解决一道习题的过程中，要看清问题的本质，并借题发挥，对问题进行变式与推广，这样才能有效地培养发现问题、提出问题、分析问题、解决问题的能力，这样的解题，才能算是一个高质量、有品位的活动，这才是一个“高大上”的解题范式。

现在的问题是，如何让学生通过借题发挥来解决问题呢？笔者认为，除了要巩固在解题教学中已取得的“从最近联想到优化思维”“从优化思维到借题发挥”等研究成果外，还要在“从借题发挥到解决问题”等方面做好文章，在更大层面上挖掘解题教学的价值。下面就“从借题发挥到解决问题”这个解题视角，谈几点具体做法。

二、几点做法

1.借发挥习题来解决问题。

借发挥习题来解决问题，就是借解决某个问题来做文章，以彰显这个问题的价值。下面以2010年无锡市中考题为例来说明这个问题。

例1：（1）如图3，在正方形ABCD中，M是BC边（不含端点B、C）上任意一点，P是BC延长线上一点，N是∠DCP的平分线上一点。若∠AMN= 90°，求证：AM=MN。

下面给出一种证明的思路，你可以按这一思路证明，也可以选择另外的方法证明。

证明：在边AB上截取AE=MC，连接ME，如图4。

在正方形ABCD中，∠B=∠BCD=90°，AB= BC。

∴∠NMC=180°-∠AMN-∠AMB

=180°-∠B-∠AMB

=∠MAB

=∠MAE。

（下面请你完成余下的证明过程）

（2）若将（1）中的“正方形ABCD”改为“正三角形ABC”（如图5），N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由。

（3）若将（1）中的“正方形ABCD”改为“正n边形ABCD…X”，请你作出猜想：

当∠AMN=°时，结论AM=MN仍然成立。（直接写出答案，不需要证明）

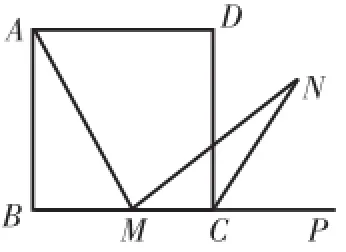
图3

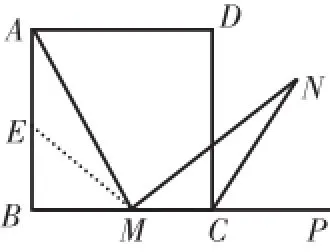
图4

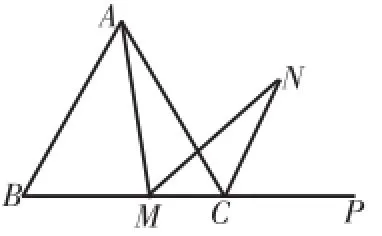
图5

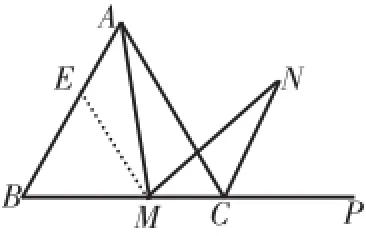
图6

【简析】（1）题中提供的方法中，已有∠NMC=∠MAE。

考虑到AE=MC，∴BE=BM，∴∠BEM=∠EMB=45°，则∠AEM=135°。

∵CN平分∠DCP，∴∠PCN=45°，∴∠AEM=∠MCN=135°。

则△AEM≌△MCN，故AM=MN。

（2）只要把问题（1）的证明思路全盘借用过来，那么（2）的结论AM=MN仍然成立。

为此，在图6中，可仍在边AB上截取AE= MC，连接ME，

∵△ABC是等边三角形，∴AB=BC，∠B=∠ACB=60°，∴∠ACP=120°。

∵AE=MC，∴BE=BM，∴∠BEM=∠EMB= 60°，∴∠AEM=120°，

∵CN平分∠ACP，∴∠PCN=60°，∴∠AEM=∠MCN=120°，

∵∠CMN=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠BAM，

∴△AEM≌△MCN，∴AM=MN。

（3）将问题拓展到正n边形ABCD…X中，这是一个认识上的飞跃，也是解决问题（1）和（2）的价值之所在。为此，我们还可以利用两角及其夹边相等来证明两个三角形全等，那么就易得

【点评】如果我们只是解决第（1）问或第（2）问，很难发现这个问题的价值，也很难将该问题推广到一个正多边形中去。但是，如果我们在解题过程中，坚持把握问题的价值，坚持厘清问题的本质，坚持变式问题的眼光，借发挥已解决过的习题来解决更加深入的问题，就一定能揭示出问题的本质，就一定会获得解题的更多精彩。

2.借发挥方法来解决问题。

借发挥方法来解决问题，是解题教学中常见的解题策略，它具有发挥迁移方法的正向导向功能。下面以2015年南京市鼓楼区一模的一道压轴题来说明借发挥方法来解决问题的价值。

例2：【问题提出】

如图7，在四边形ABCD中，AD=CD，∠ABC= 120°，∠ADC=60°，AB=2，BC=1，求四边形ABCD的面积。

【尝试解决】

旋转是一种重要的图形变换，当图形中有一组邻边相等时，往往可以通过旋转解决问题。

（1）如图8，连接BD，由于AD=CD，所以可将△DCB绕点D顺时针方向旋转60°，得到△DAB'，则△BDB'的形状是。

（2）在（1）的基础上，求四边形ABCD的面积。

【类比应用】

如图9，在四边形ABCD中，AD=CD，∠ABC=75°，∠ADC=60°，AB=2，BC=2，求四边形ABCD的面积。

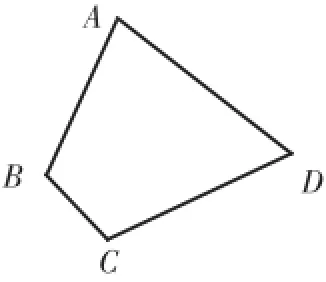
图7

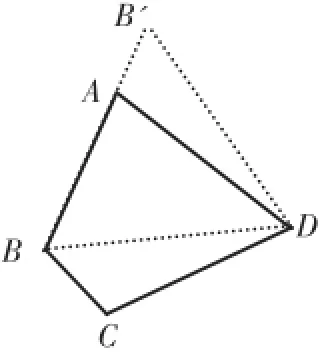
图8

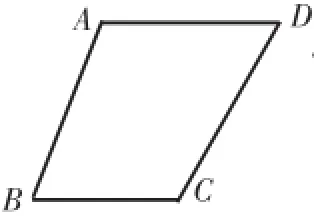
图9

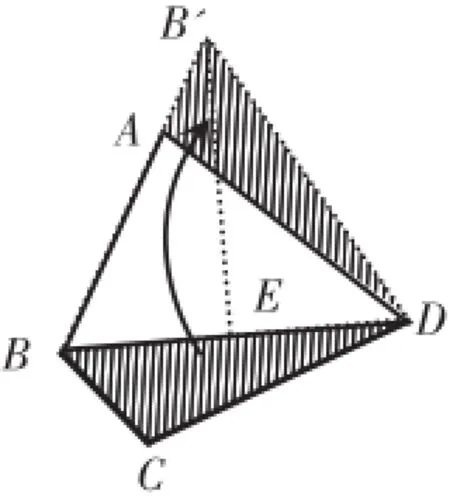
图10

【简析】尝试解决：

（1）借用旋转的性质，易得△BDB'是等边三角形。

（2）如图10，∵AD=CD，∴旋转后点A和点C重合。

∵四边形ABCD中，∠ABC+∠ADC=180°，

∴∠BAD+∠BCD= 360°-180°=180°。

由旋转得：∠BCD=∠B'AD，

∴∠BAD+∠DAB'=180°，即B、A、B'在同一条直线上。BB'=AB+AB'=AB+ BC=3，∴等边△BDB'的边长为3，

过B'作等边△BDB'的高B'E，∵∠ABD=

类比应用：

由于本问题与“尝试解决”有异曲同工之处，所以仍可连接BD，由于AD=CD，可将△BCD绕点D顺时针方向旋转60°，得到△DAB'，则△BDB'是一个等边三角形。（具体过程略）

不过，连接DB后，我们也可将△DAB绕点D逆时针旋转60°到△DCB'，如图11。

由旋转同（1）可得：CB'=AB=2，△BDB'是等边三角形。

∵四边形ABCD中，∠BAD+∠BCD=360°-（60°+75°），∠BAD=∠B'CD。

∴∠B'CB=360°-［360°-（60°+75°）］=135°。正因为∠B'CB=135°，才使问题出现了转机，此时，我们可以根据135°角构造一个锐角为45°的直角三角形，使问题解决看到了希望。因此，可过B作BE⊥CB'，∴∠BCE=180°-135°=45°。

∵BC=2，∴BE=CE=BC·sin45°=1。

∵Rt△BEB'中，∠E=90°，BE=1，B'E=3，

∵S四边形ABCD=S△BDB'-S△BCB'，

∴S四边形ABCD=

【点评】本题充分展示了旋转变换这一解题方法在解题中的价值。在“尝试解决”这个环节中，由于条件的特殊性，旋转后B、A、B'三点在同一条直线上，为解决问题提供了有利的方法。到“类比应用”这个环节中，旋转后B、A、B'三点不在同一条直线上，这对解决问题增加了难度。但是在旋转后，发现∠B'CB=135°，这又为解决问题提供了转机。如果在一个结构里研究这个问题的话，不难发现，无论旋转后B、A、B'三点是否在一条直线上，∠B'CB的度数必须是一个特殊角，我们才能不用三角函数表或不用计算器有效地解决问题。如果不是特殊角，那么就必须借助三角函数表或计算器或再提供一些所需要的三角函数值，才能顺利地解决问题。在这个过程中，我们可以清楚地看到借发挥方法来解决问题的魅力所在。

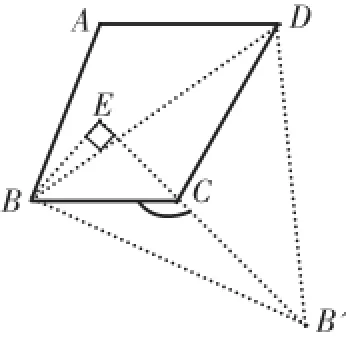
图11

3.借发挥本质来解决问题。

数学本质是高观点下的数学属性，它是对数学概念的精准把握，是对定理法则的高度诠释，是对思想方法的哲学定位。因此，借发挥本质来解决问题，是数学解题的最高境界。下面以南京市高淳区的一道初二期末试题来说明这个道理。

例3：已知点M、N分别是正方形ABCD的边CB、CD的延长线上的点，连接AM、AN、MN，∠MAN=135°。

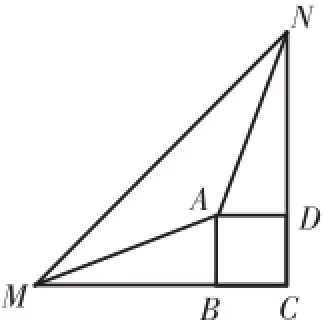
图12

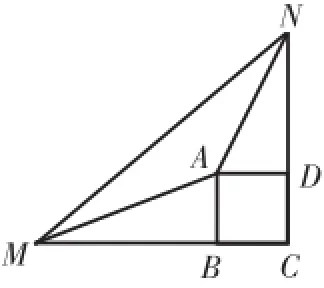
（1）如图12，若BM=DN，求证：MN=BM+ DN。

（2）如图13，若BM≠DN，试判断（1）中的结论是否仍成立？若成立，请给予证明；若不成立，请说明理由。

【简析】（1）解决“MN=BM+DN”这类问题，学生凭经验不外乎是用“截长补短”法。因此，有一部分学生会采用下列方法来解决问题（1）。

作AE⊥MN，垂足为E，如图14，这样就把线段MN截成EN和NM两个部分，此时可用“截长法”来解决问题。

由四边形ABCD是正方形得，AD=AB，BC= CD，∠ADC=∠ABC=90°，

则∠ADN=∠ABM=90°。

在△ADN与△ABM中，由于AD=AB，∠ADN=∠ABM=90°，DN=BM，

∴△ADN≌△ABM，则AN=AM，ND=MB。

又∠MAN=135°，AN=AM，

∴∠ENA=∠EMA，

又BC=CD，ND=MB，则∠NCM=90°，

∴∠CNM=∠CMN=45°，而∠ENA=∠EMA= 22.5°，

∴∠ENA=∠EMA=∠BMA=∠DNA=22.5°，

则△ENA≌△EMA≌△BMA≌△DNA。

∴DN=BM=EN=EM。

∴MN=EN+EM=BM+DN。

这种方法是基于△ADN≌△ABM形成了“∠ENA=∠EMA=∠BMA=∠DNA=22.5°”这样一个特殊的数量关系而得到问题（1）结论的。

如果将这种方法迁移到问题（2）中去就很难奏效了。原因何在？是因为问题（1）的证明方法没有揭示出问题本质，它只是一个“技巧”而已。这个技巧就是能够得到△ENA≌△EMA≌△BMA≌△DNA。当BM≠DN时，△ENA、△EMA、△BMA、△DNA这几个三角形就不全等了，所以问题（1）的方法不灵了。那么，这道题的数学本质在哪儿？既然用“截长”揭示不出问题的本质，那么就用“补短”的方法试试。延长BC到点P，使BP=DN，连接AP，如图15。通过证△ABP≌△ADN、△ANM≌△APM解决问题。具体证法如下：

（2）若BM≠DN，（1）中的结论仍成立，理由如下：

在如图15中，∵四边形ABCD是正方形，

∴AB=AD，∠ABC=∠ADC=∠BAD=90°，

∴∠ADN=90°。

在△ABP与△ADN中，∵AB=AD，∠ABP=∠ADN，BP=DN，

∴△ABP≌△ADN，

∴AP=AN，∠BAP=∠DAN。

∵∠MAN=135°，

∴∠MAP=∠MAB+∠BAP=∠MAB+∠DAN= 360°-∠MAN-∠BAD=360°-135°-90°=135°，

∴∠MAN=∠MAP。

在△ANM与△APM中，∵AN=AP，∠MAN=∠MAP，AM=AM，

∴△ANM≌△APM，

∴MN=MP。

∵MP=BM+BP=BM+DN，

∴MN=BM+DN。

图14

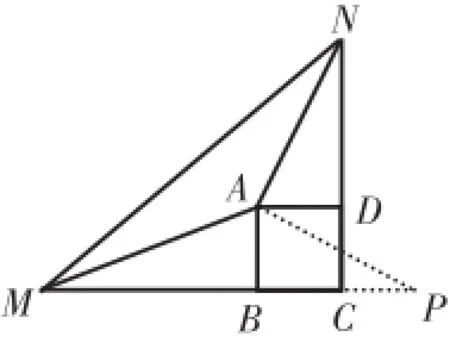
图15

【点评】解题教学关注的要点固然很多，在这里要强调的是，根据题意寻求数学问题本质的解法不能少。就本题而言，解决问题（1）的方法虽然能让学生得到一定的“考试分数”，但用它去解决问题（2）就不行了，那是因为它缺少逻辑连贯的本质，为此有必要寻找出揭示数学本质的方法来解决问题（2）。在学生得到本质解法后，再让学生回过头来用解决问题（2）的方法去解决问题（1），学生必然会在这个思维过程中，体会到本问题中数学本质的恢弘气势，这也为学生在以后的解题中，探究问题的数学本质提供了动力倾向。

三、教学思考

解题教学有一种倾向，就是选择的习题，总喜欢在“大题”“难题”“量多”上做文章，认为这样才能有效训练学生的思维，才能使学生经得起任何形式的考验。其实不然，从上面分析可以看出，习题教学还要兼顾“借题发挥来解决问题”。因此，在习题教学中，笔者认为还要把握好下面三个要点。

1.题不在大，有魂则灵。

习题教学中选择的题，不一定要是“大题”，但要选择那些能够让数学思想方法贯串在其中的经典习题，供学生探究。就是说，一要选择解法自然的问题，让学生自然地想到解题方法，这种方法不是教师强加给学生的方法，而是学生的“思维必然”，是学生根据题目中的条件自然产生的解题方法，并且这种方法还能迁移到类似的问题中去，让学生解一题，懂一法，会一类。即使是新的解题方法，那么这种方法，一定要有较强的迁移性和广泛的适用性。二要选择能揭示数学本质的问题，让学生在解题过程中，看清数学的本来面貌，自然地结构化数学知识，这样学生就有举重若轻的感觉。上面说的两点，事实上就是“题魂”，因此，有“题不在大，有魂则灵”一说。

2.题不在多，有法才行。

如何控制习题教学中的题量，是习题教学的又一个值得研究的问题。解题的价值不在题量的多少，而在于解题方法的形成和解题方法本身的价值。

合适的解题方法，源于对数学概念的理解、对法则定理的运用、对已有解题方法的迁移的灵活度和对题目中条件与结论关联的灵敏度。解题方法本身的价值，源于本方法的应用性和迁移性，最好能形成在某些条件下的“通性通法”。对于一些特殊的解题技巧，教学中要有机提炼，不可盲目追求。要注意技巧要在通性通法上形成，让学生首先“想得到”，其次是“想得妙”。如例3中的解题方法，既可以是一种通法，也可算是一种技巧，学生在解决例3的过程中，才会感受到通法与技巧的关系，才能再次积累一些解题经验。

3.题不在难，有为就可。

同样，习题教学中还有一个难度控制的问题值得重视和研究。解决这个问题关键要在“为”字上去把握和选择。“为”就是解决问题的作为，这个作为就是数学内在的本质，在解题教学中揭示数学本质，就是解题活动的根本目的。如果解题教学只是简单地追求问题的结果，不去追求思维的价值，必然会淡化解题教学的价值。如例3中第（1）问的解答，在某种程度上也能得到问题的答案，但那只是一个答案而已，如果变换一下“马夹”，就不知所然了，原因就是解答过程没有揭示数学本质。

提出“从借题发挥到解决问题”的教学主张，就是想从提供的问题中寻找到攻破问题的钥匙，这个钥匙就是数学本质，让学生能自觉地用这个数学本质去真正地解决问题。

（作者为江苏省中学数学特级教师，正高级中学教师，现任教于江苏省南京市宁海中学分校）