“同题”如何“异构”

◇　江苏　刘业峰



“同题”如何“异构”

◇江苏刘业峰

同题”是同一个问题或课题,“异构”是不同的结构．在课堂教学中,“异构”可以是同一课题的不同教学结构设计,也可以是同一物理问题的“变形”设计．开展同题异构活动就是希望通过教师的创造性工作,引领学生在学习的过程中碰撞出智慧的火花,从而实现激发学习兴趣,调动学生学习的主动性、积极性与创造性,以实现提高发现问题解决问题的能力和培养科学素养的教育目标．

那么如何“异构”呢?下面通过一次以“带电体在磁场中的运动”为课题的“同题异构”教学活动来探讨物理问题的“同题”怎样“异构”．

原题1如图1所示为一边长为2a的正三角形ABC区域,该区域存在磁感应强度为B,方向垂直纸面向里的匀强磁场．一质量为m，电荷量为e的电子沿平行于底边BC且通过AB的中点D射入磁场．现发现电子垂直BC边穿出,试求该电子的初速度v的大小．

图1

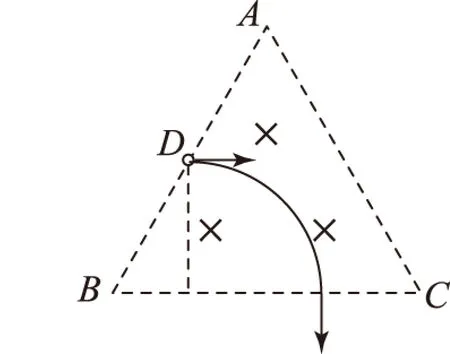
图2

1) 拓宽延伸可以异构.

异构1保持电子的入射位置及速度方向不变,要保证电子能从BC边射出,则电子的初速度v的大小应满足什么条件?

图3

图4

2) 数理结合可以异构.

异构2保持电子的入射点位置及速度方向保持不变,若要保证电子能从BC边射出,试证能从BC边射出的电子的运动轨道的最大半径所对应的圆,与BC相切于C点．

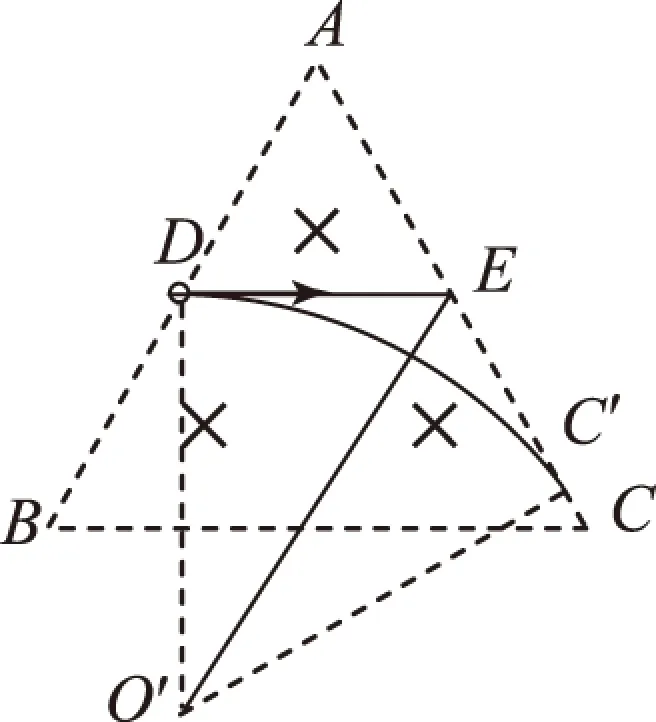
图5

证法1假设粒子的轨迹于AC相切于C′点．过D作圆轨迹的切线交AC于E．

△DO′E≌△C′O′E,对应边DE=EC′．在△ADE中,DE=a．故EC′=a．

又由题知EC=a．得证C、C′重合，即相切于C点．

图6

证法2建立如图6所示的坐标系,原点在DO′与BC的交点处．电子圆周运动的轨迹经过C点,现证明C点为切点．设轨迹的圆心为O′,连接O′C为半径．

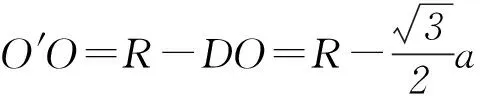
直线AC斜率

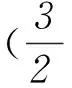
与圆轨迹方程联立得

(2x-3a)2=0,

3) 由特殊到一般可异构.

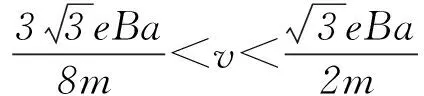
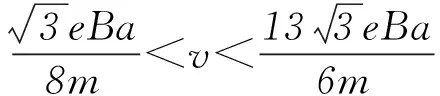
图7

图8

4)变化物理图景是异构．

异构4在直角三角形ABC中有垂直纸面向里的磁场(图9),有一电子束以大小不同的水平速度射向AB的中点D．在图中标出在边界ABC上有电子穿出的区域．

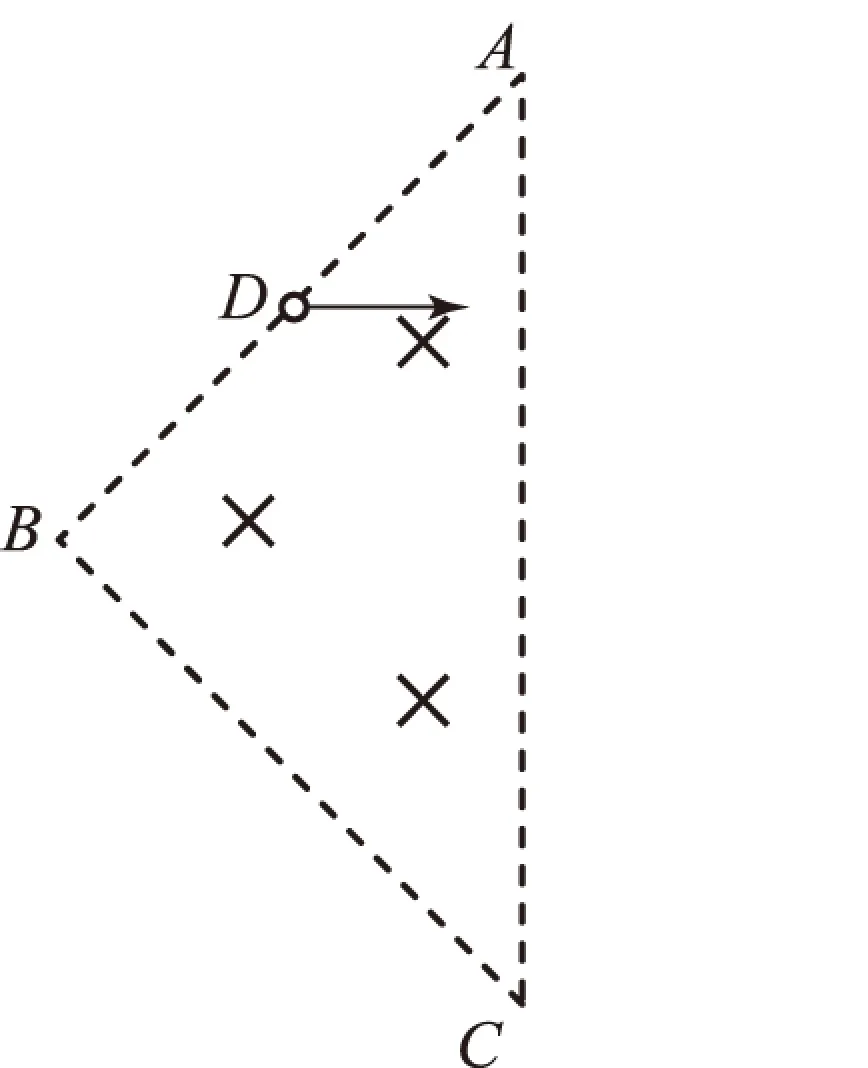
图9

图10

5) 分情形讨论也是异构．

异构5图11所示的区域有垂直纸面向里的磁场．一束电子以相同的速度水平射向磁场,并且已知电子全部从A—O—B—D边界穿出．其中靠近AC边界入射的电子的轨迹如图11所示．在图中画出几条具有简单特征的电子运动轨迹．(∠CAO=∠DBO=135°)

(1)电子从AO边界射入，从AO边界射出;

(2)电子从AO边界射入，从OB边界射出;

(3)电子从OB边界射入，从OB边界射出;

(4)电子从OB边界射入，从BD边界射出．

4种情况中简单而且具有典型意义的电子运动轨迹如图12所示．

图11

图12

当然也可以利用类比、逆向思维、等效等进行异构．“异构”激发了教师的创新意识、创造激情和工作热情，但“异构”不应成为教师个人的智力游戏,也不单单只是训练学生能够灵活解决新问题的能力，而应是希望通过“异构”使学生获得灵感的激发,调动学生全身心投入到课堂教学中,体会并实践物理学的基本思想与方法,从而发现问题并提高解决问题的能力．因此引领学生投入到物理学习与研究中，从而实现学生“自主异构”，这是教师“异构”更高层次的工作任务．

学生的质疑是引领“自主异构”最简单、最基本的出发点．

原题2在场强为B的水平匀强磁场中,一质量为m、带电荷量为Q的小球在O点静止释放,小球的运动曲线如图13所示．已知此曲线在最低点的曲率半径为该点到x轴距离的2倍,重力加速度为g,求:

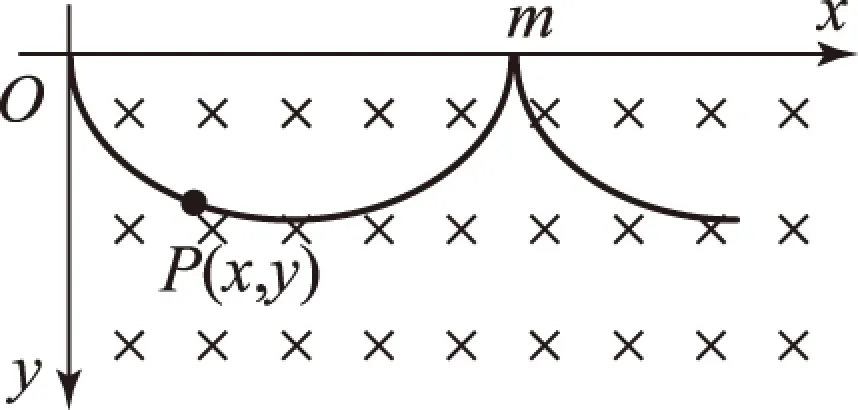
图13

(1) 小球运动到任意位置P(x,y)处的速率．

(2) 小球在运动过程中第1次下降的最大距离ymax．

(原题解答略)

1) 学生质疑1.

当满足一定前提条件下,是不是可以出现这样的轨迹,小球先做加速曲线运动，然后做水平匀速直线运动．

异构1在场强为B的水平匀强磁场中,一质量为m、带电荷量为Q的小球在O点静止释放,对于其在磁场中的运动轨迹,甲、乙2位同学做了如下讨论:

学生甲:不可能出现小球先做加速曲线运动，然后做水平匀速直线运动,因为如果出现这样的轨迹,假设在M点开始匀速运动,那么M点也是曲线运动的末时刻,可看成一段圆弧的圆周运动，有

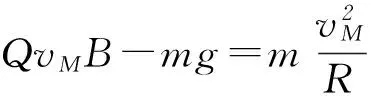
匀速运动到N点,在N点有

QvNB-mg=0,

故vM≠vN,M到N不是匀速运动．

学生乙:从开始下落到M点的过程中是一个曲率半径变化的曲线运动．在M点有

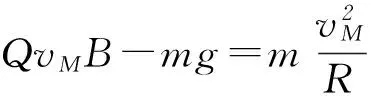
其中R→∞,则QvMB-mg=0．

在N点有QvNB-mg=0．得vM=vN,即最后小球能够做匀速直线运动．

对于2位同学的讨论该如何评价呢？

图14

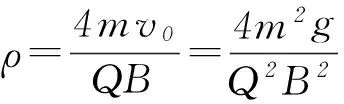
即最低点的曲率半径ρ为圆周运动半径R的4倍．故最低点的曲率半径为一个有限值,同学乙的论述错误．同学甲没有定量地计算出曲率半径，因此也不能说服乙．

2) 学生质疑2.

能不能确定某一时刻物体的位置与速度呢?

v1=v1x=v0．

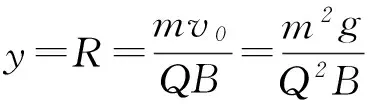
分速度为v2=v2y=v0. 将2个分运动合成起来其位置坐标为

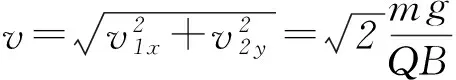
“同题异构”活动通过教师的创造性劳动引领调动学生参与异构中，使之学会思考、学会研究，激发其学习的主动性、积极性和创造性．学生在享受“伟大”发现的成功喜悦的同时，知识得到了收获，能力得到了提升，同时拓展了思维的发散性、独立性和批判性．

在“异构”中,“异构”不要简单地成为“脑筋急转弯”或者“灵感”的闪现,要紧密围绕物理学科的基本思想、基本方法的主线，使“小技巧”成为“大智慧”，如此才能增强同学科学意识,培养科学素养．这要求课堂教学的结构设计以物理思想为依托,以解决理论问题、实际问题为主线,引领学生在学习过程中提高能力，收获知识，这也正是物理教育工作者最值得进行创造性劳动之所在．

江苏省昆山中学)