叠堆式压电陶瓷驱动器的复合控制

刘长利，胡守柱*，郭海林，王学军，2，章文俊，3

(1.华东理工大学 机械与动力工程学院，上海 200237；2.美国哥伦比亚大学 机械工程系， 美国 纽约 10027；3.萨斯喀彻温大学 机械工程系， 加拿大 萨斯卡通 250101)



叠堆式压电陶瓷驱动器的复合控制

刘长利1，胡守柱1*，郭海林1，王学军1，2，章文俊1，3

(1.华东理工大学 机械与动力工程学院，上海 200237；2.美国哥伦比亚大学 机械工程系， 美国 纽约 10027；3.萨斯喀彻温大学 机械工程系， 加拿大 萨斯卡通 250101)

提出了逆Bouc-Wen前馈控制与反馈控制相结合的复合控制算法，用于改善压电陶瓷驱动器对目标轨迹的跟踪性能。建立了压电陶瓷驱动器的Bouc-Wen迟滞动力学模型，并用粒子群算法(PSO)对该模型的参数进行识别。基于Bouc-Wen迟滞模型，提出了逆Bouc-Wen前馈补偿控制。最后，为消除迟滞模型的不确定性，引入比例积分(PI)反馈控制，并与前馈补偿控制构成复合控制算法。建立了基于dSPACE实时系统的压电陶瓷驱动实验平台，迟滞实验结果表明：压电陶瓷的迟滞误差量几乎为0，线性度高达96.5%；目标轨迹跟踪实验结果表明：复合控制算法的最大跟踪误差为0.180 5 μm，均方根(RMS-Root mean square)跟踪误差为0.055 4 μm，跟踪精度达到了10-8m。相比于开环控制、前馈控制及PI反馈控制，提出的复合控制算法能够基本消除压电陶瓷的迟滞非线性，同时具有很好的轨迹跟踪性能。

压电陶瓷驱动器；参数辨识；复合控制；轨迹跟踪；Bouc-Wen模型

1　引　言

压电陶瓷在超高精度定位领域应用广泛，主要应用于微动平台(微动机器人)的驱动，如细胞操作，微/纳机电系统(MEMS)及超精密加工等[1-2]。对压电陶瓷驱动器的精密跟踪控制是实现超高精度定位的关键。然而，压电层片驱使压电陶瓷伸长，将产生迟滞非线性现象，不可避免地会在系统定位过程中产生定位跟踪误差，影响整个系统的定位操作性能[3]。针对压电陶瓷迟滞非线性影响微动平台终端定位精度的问题，国内外学者主要通过控制补偿的方法解决该问题，主要分为两大类：一是利用电荷控制的方法减小压电陶瓷迟滞非线性，基于压电陶瓷输出位移与其自身所带电荷量成呈线性关系的原理，控制驱动器的输出电荷量，达到线性控制的目的[4]，但由于电荷型驱动电源电路复杂，存在漏电现象，无法保持压电陶瓷两端自由电荷稳定等缺点，使其应用受限[5]。二是采用电压控制的方法，默认驱动电压与压电陶瓷输出位移呈近似线性关系，为了避免迟滞非线性对压电陶瓷输出位移的影响，建立迟滞非线性的数学模型对迟滞进行描述，如PI模型，Duham模型、Bouc-Wen模型以及Maxwell模型等[6]，利用其逆模型前馈补偿控制对电压进行补偿，来减小迟滞非线性[7-8]。但是由于提出的模型的局限性及参数辨识准确性等问题，不能准确地表达压电陶瓷迟滞非线性现象。为了进一步提高压电陶瓷驱动的微动平台定位精度，采用反馈控制的方法进行补偿，如常用的PID控制[9]；其次各种智能控制算法的反馈控制补偿的应用进一步提高定位精度，如模糊控制，神经网络控制及滑模控制等[10-11]。然而，上述反馈控制补偿的方法基于微动平台终端输出位移的压电陶瓷反馈控制补偿，未考虑压电陶瓷模型误差与微动机构终端输出误差的累计误差的影响。

为了克服上述问题，提出压电陶瓷驱动器的复合控制算法。首先，建立压电陶瓷的位移测量系统，用于提供压电陶瓷实时的位移输出响应；其次，建立压电陶瓷驱动器的Bouc-Wen迟滞动力学模型[12]，并用粒子群算法对该模型的参数进行识别，提出逆Bouc-Wen模型前馈控制与PI反馈控制的复合控制算法。一方面，相比单一的迟滞模型描述压电陶瓷迟滞现象，Bouc-Wen迟滞动力学模型更适用于动态轨迹跟踪控制；另一方面，基于应变测量系统的反馈控制可以补偿迟滞模型的不确定误差。最后，建立dSPACE实时系统实验平台，对目标参考轨迹进行跟踪实验，并与无补偿控制、前馈控制及PI反馈控制的实验结果比较。

2　位移测量系统

为了测量压电陶瓷在驱动电压下的位移变化，在压电陶瓷两侧黏贴封装应变片，构成惠斯顿全桥应变测量电路，如图1所示[13]。

图1　压电陶瓷的惠斯顿全桥位移测量

Fig.1Displacement measurement system of Huis whole bridge using strain gauges

其中：激励电压VEX与应变桥路输出电压V0关系为：

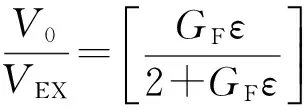
(1)

其中：假设每个应变片的标称阻值都相同即R1=R4=R2=R3=RG，R1和R4为变应变片，R2和R3为固定阻值的补偿应变片，ΔR为应变片的变化阻值，GF应变系数，ε为应变。

由式(1)可得压电陶瓷驱动位移计算公式：

(2)

其中：Δl为压电陶瓷驱动输出位移，L为叠堆式压电层片总厚度。

考虑压电材料垂直于驱动伸长方向会产生缩短(或伸长)变形，引入泊松比ν：

(3)

式(3)即为压电陶瓷驱动位移变化量的计算公式，可用于控制反馈下计算压电陶瓷输出位移。

3　迟滞动力学模型及其参数辨识

为了更好的表达压电陶瓷的动态位移输出特性，建立含迟滞模型的动力学模型。

3.1迟滞动力学模型

王代华等人[14]认为压电陶瓷的输出位移可看做线性分量与迟滞分量的叠加：

x(t)=du-h，

(4)

其中：x(t)为压电陶瓷输出位移，d为压电系数，u为压电陶瓷驱动电压，h表示迟滞位移分量。利用Bouc-Wen迟滞算子模拟迟滞位移分量：

(5)

其中：α，β，γ是决定迟滞非线性形态参数，对于塑性材料n=1。为了简化系统，不考虑全局扰动，即p=0。

当对压电陶瓷驱动器施加驱动电压，其输出可以被看做一驱动力发生器，因此叠堆式压电陶瓷每一压电层片都可以等效成一个质量-弹簧-阻尼系统，多个压电层片串联而成的压电陶瓷等效动力学模型如图2所示。考虑其迟滞非线性，采用式(4)对压电陶瓷驱动器动力学模型加以改进，形成迟滞动力学模型：

(6)

其中：m，c，k为压电陶瓷所有层片的质量、阻尼、弹性系数，x为压电层片总的输出位移。

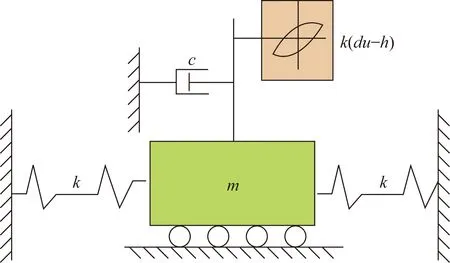
图2　压电陶瓷驱动器迟滞动力学模型

3.2迟滞动力学模型参数辨识

为了得到压电陶瓷迟滞动力学模型，采用粒子群(PSO)优化算法对m，c，k，d，α，β和λ7个参数进行辨识，粒子群算法相对直接搜索法和遗传因子法具有很多优点，如辨识速度快和精度高等[15]。

粒子的适应度函数为：

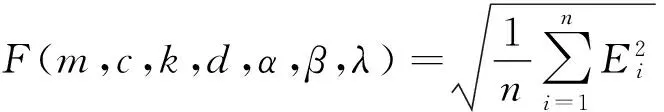
(7)

(8)

整个模型参数辨识过程在MATLAB/Simulink中完成，其中 Bouc-Wen 模型用Simulink实现，粒子群算法通过在MATLAB中调用PSO工具包实现。通过实验采集实际迟滞环的数据，利用粒子群算法对理论迟滞动力学模型参数进行辨识，辨识流程如图3所示。辨识结果如表1所示。其中，Present表示参数识别当前值， pBest参数识别局部最优值，gBest 参数识别全局最优值。

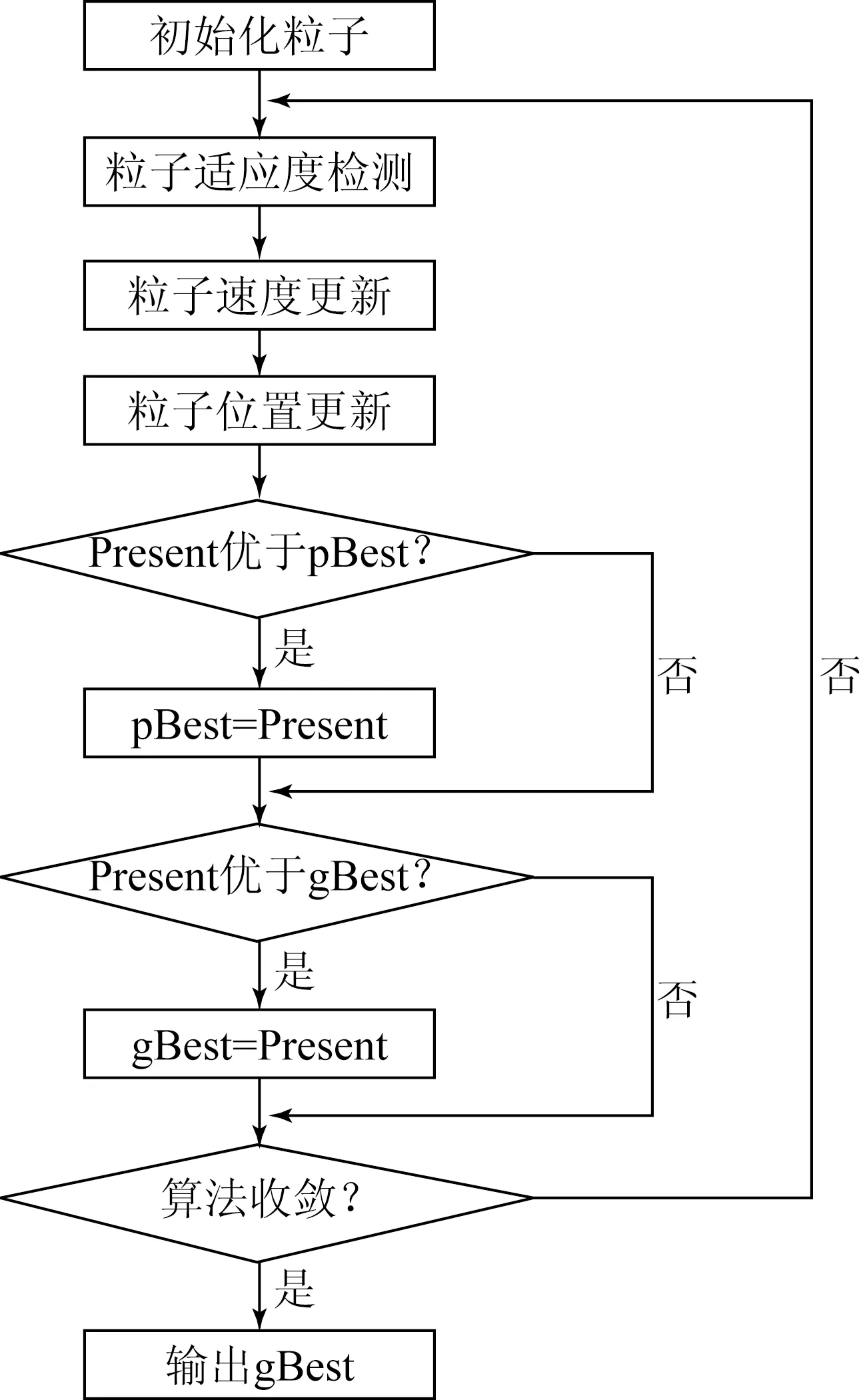
图3　迟滞动力学模型PSO参数辨识流程图

模型参数(单位)寻优范围数值m/kg0.1～0.20.1651c/(Ns·m-1)0～100k(×106N/m)5～65.9930d(×10-7m/V)0～51.0970alfa0～10.2211beta0～10.0179gama0～10.0195

驱动电压在0～100 V内，Bouc-Wen模型迟滞环与实验迟滞环如图4所示。由图4可知，Bouc-Wen模型可以较好地描述实际迟滞环。但是由于模型的局限性，Bouc-wen模型的迟滞环与实验迟滞环两端存在的最大模型偏差为0.381 μm，模型均方根误差值为0.090 3 μm。为了进一步消除模型不准确带来的误差，可以通过反馈控制的方法进行补偿。

图4　实验迟滞环与Bouc-Wen模型迟滞环比较

4　复合控制算法

4.1逆Bouc-Wen模型前馈补偿控制

逆Bouc-Wen模型的前馈补偿控制((H-1) FF)，用于补偿压电陶瓷的迟滞非线性。该前馈补偿的方法是在实际的迟滞环中考虑逆迟滞算子ζ-1，其中迟滞算子ζ描述理论迟滞环，可由3.2节中Bouc-Wen模型的辨识结果得到。迟滞补偿为：

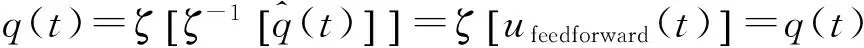
(9)

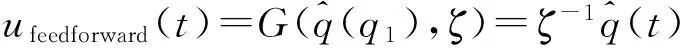
(10)

(a) (H-1) FF控制原理框图

(a) (H-1)FF control block diagram

(b)迟滞模型与逆迟滞模型的线性化关系

4.2复合控制算法的实现

逆Bouc-Wen模型的(H-1) FF的控制和PI反馈控制结合的复合控制算法，如图6所示。其中的PI反馈控制环节，将实际输出位移与期望输入位移之间的误差e作为PID控制器的输入，获得补偿电压ue驱动压电陶瓷，此时该复合控制算法输出的驱动电压为u=ufeedforward+ue，这将使压电陶瓷的输出位移更加精确，对轨迹的动态跟踪性能更好。

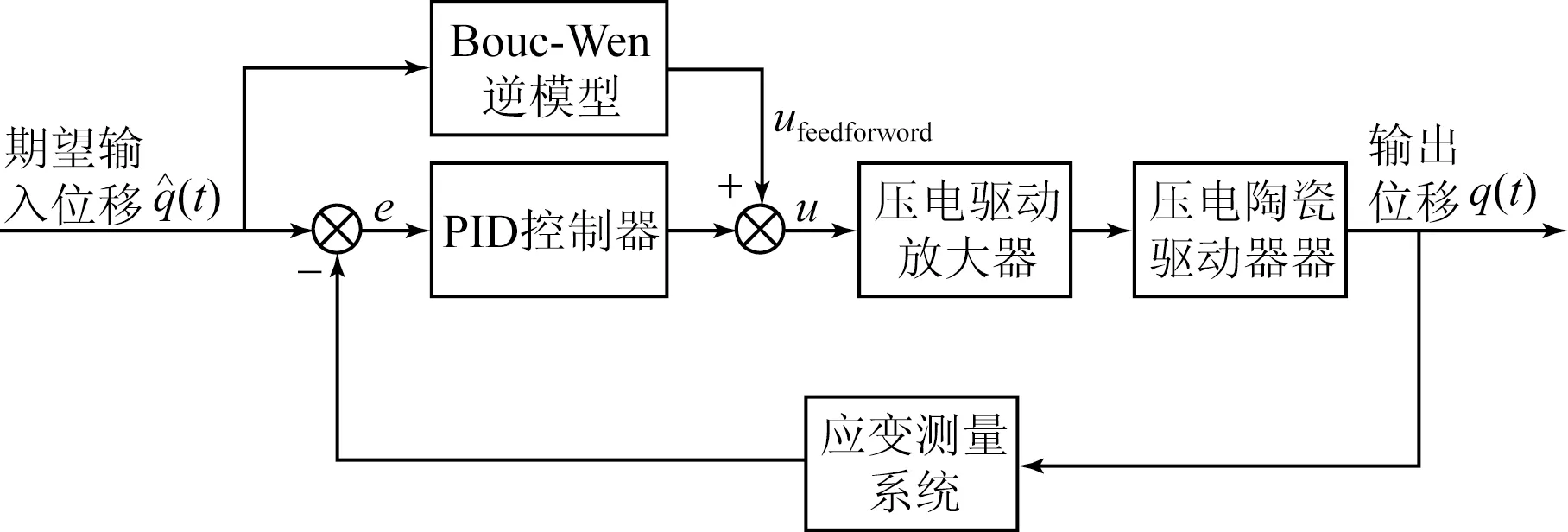
图6　(H-1) FF控制和PI反馈控制的复合控制算法

逆Bouc-Wen模型前馈补偿的复合控制方法可以有效的补偿压电陶瓷的迟滞非线性，而且PI反馈控制可以消除模型辨识带来的误差，从而满足了压电陶瓷驱动器高精度轨迹跟踪控制的要求。

5　实验过程及结果

5.1实验装置

为了辨识压电陶瓷的迟滞动力学模型，以及验证复合控制算法对目标轨迹跟踪性能，建立了基于dSPACE实时系统的压电陶瓷驱动实验平台，实验装置与硬件接线原理如图7所示。

(a)压电陶瓷驱动实验平台

(b)硬件接线示意图

实验中压电陶瓷采用索雷博的PZS001，最大伸长输出位移为(17.4±2) μm；压电陶瓷驱动放大器为德国PI公司的E503型号，驱动器产生-20～120 V电压；应变电路及信号调整放大电路为自行研制；dSPACE实时系统选用DS1103 PPC控制器内置D/A、A/D模块实现数据采集和实时控制任务。

5.2实验结果

为了验证该复合控制算法对压电陶瓷迟滞非线性的改善情况，以及评估对目标轨迹的跟踪性能，分别对压电陶瓷采用无补偿控制(Without compensation)、前馈控制 ((H-1) FF)、PI反馈控制(PI)及复合控制(PI+(H-1) FF)，要求压电陶瓷的目标轨迹为一组频率为1 Hz、幅值为10 μm 的正弦曲线，压电陶瓷驱动器实际输出位移如图7(a)所示。

定义压电陶瓷的最大迟滞误差和线性度为：

(11)

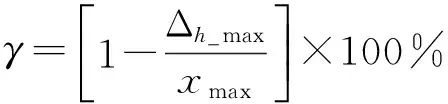
(12)

其中：x(t)为压电陶瓷实际输出位移，xfitted(t)为最小二乘拟合输出位移，xmax实验输出位移的最大值。

由图8(a)的迟滞曲线图以及图8(b)的曲线线性度可知，压电陶瓷的迟滞非线性不可避免。但与开环无补偿控制比较，前馈控制可以明显减小迟滞误差，最大迟滞误差为0.153 61 μm，相对于原有的迟滞误差减少约84.3%，线性度为85%。PI反馈控制依旧存在迟滞误差，线性度为89.7%。复合控制的方法的迟滞误差最小约为0，线性度提高到96.5%。

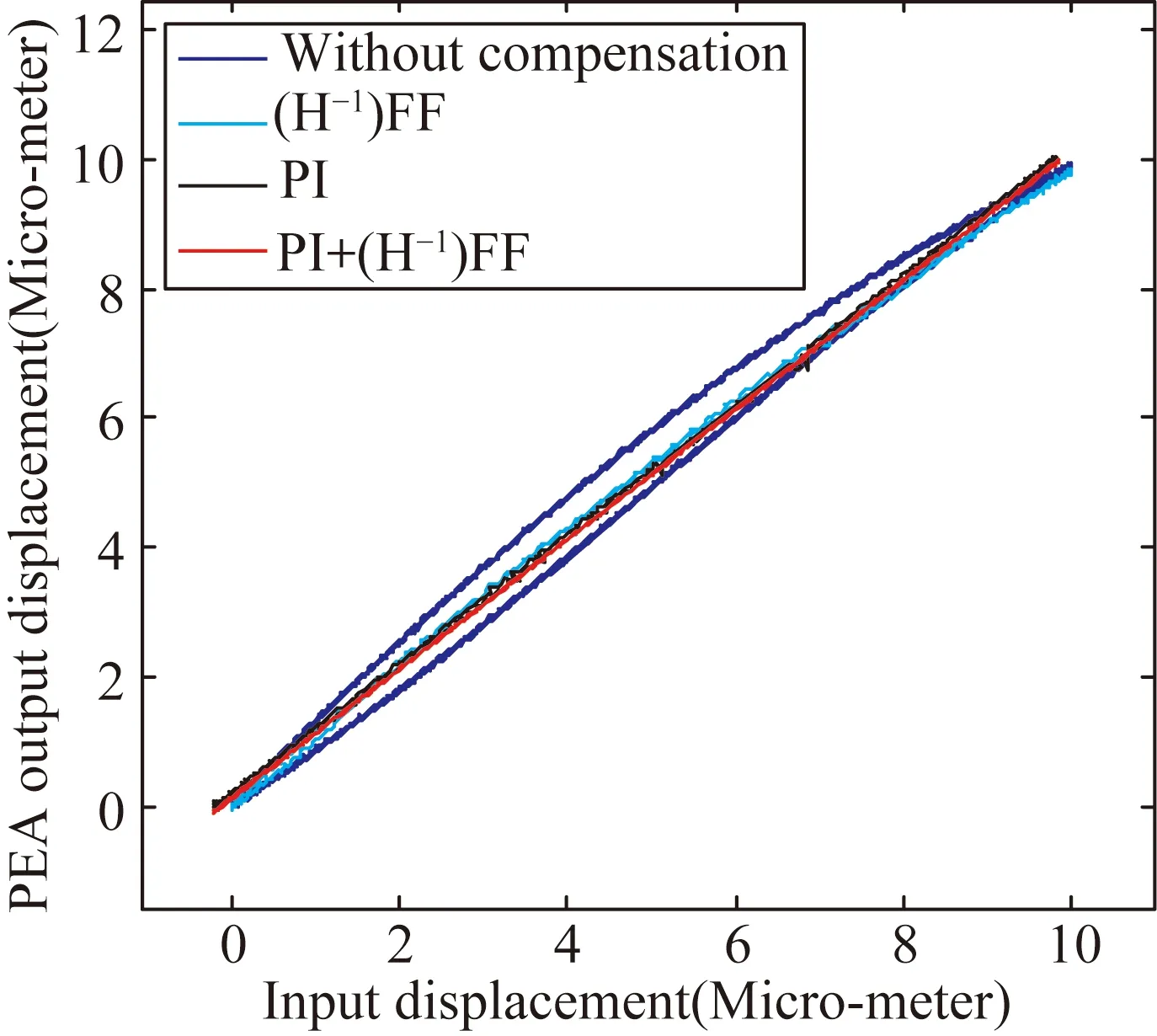
(a)迟滞曲线

(b)线性度

为了验证复合控制算法的跟踪性能，目标轨迹如图9(a)所示，采用开环无补偿控制(Without compensation)、前馈控制 ((H-1) FF)、PI反馈控制(PI)及复合控制(PI+(H-1) FF)，分别对该轨迹进行跟踪，实验结果如图9(b)所示，跟踪误差如图9(c)所示。几种控制方法的最大误差和均方根误差如表2所示。由表2可知，复合控制方法的跟踪性能最好。

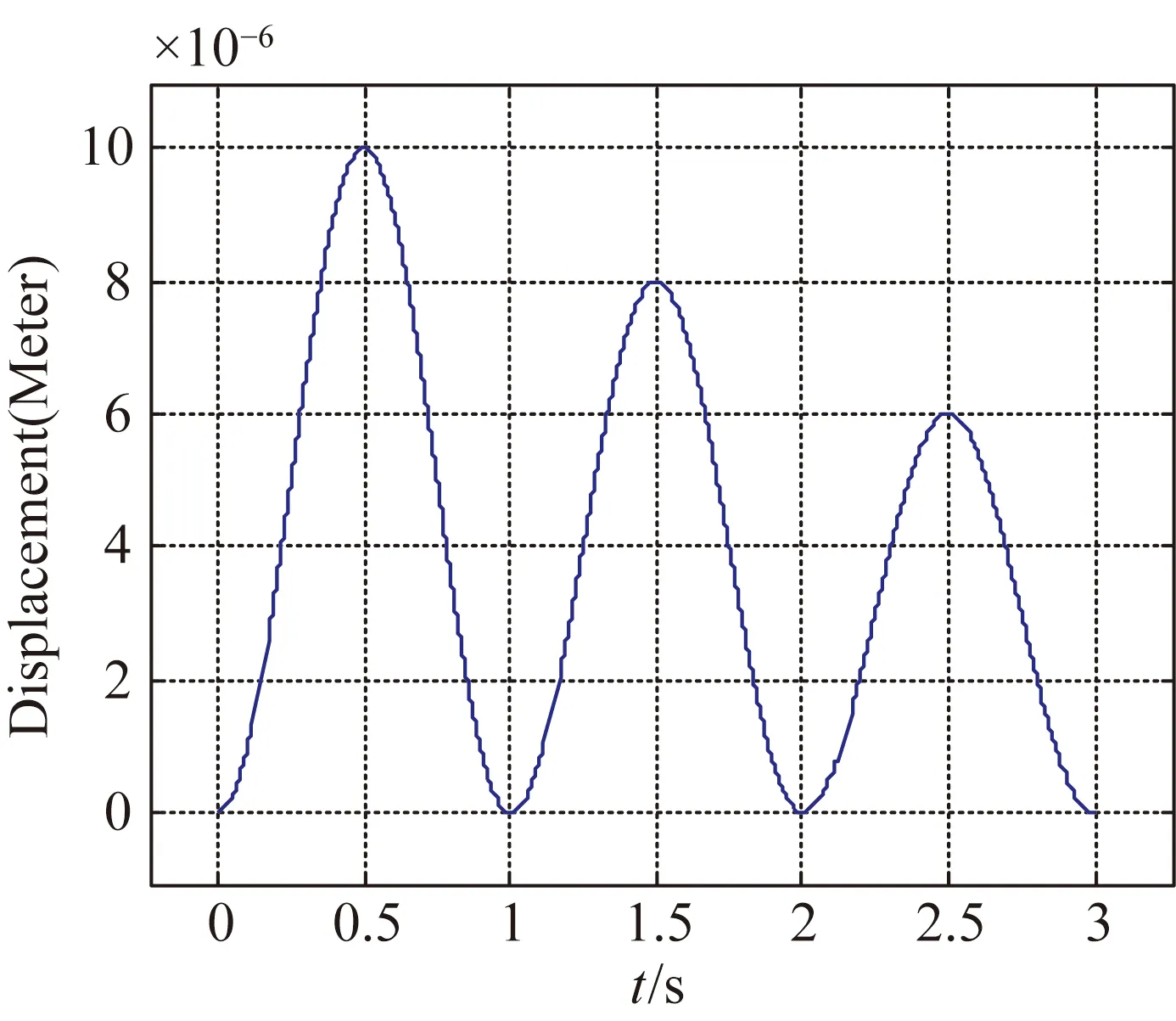
(a)目标轨迹

(b)轨迹跟踪结果

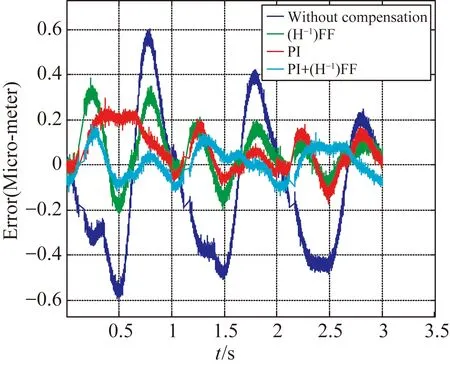
(c)曲线跟踪误差结果

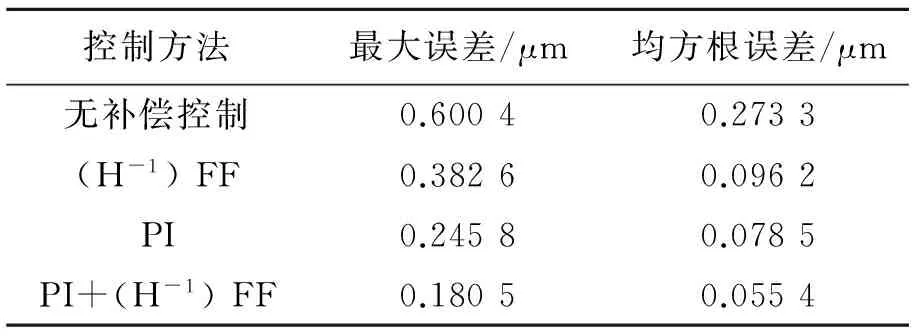
控制方法最大误差/μm均方根误差/μm无补偿控制0.60040.2733(H-1)FF0.38260.0962PI0.24580.0785PI+(H-1)FF0.18050.0554

6　结　论

为了提高压电陶瓷驱动器的轨迹跟踪性能，提出了逆Bouc-Wen前馈控制与反馈控制相结合的复合控制算法，并应用于压电陶瓷驱动器轨迹跟踪控制。迟滞实验结果表明，在复合控制算法控制下，压电陶瓷迟滞误差几乎为零，线性度高达96.5%；对目标轨迹的跟踪结果表明，复合控制算法的最大跟踪误差为0.180 5 μm，仅为无补偿控制的30%左右，均方根(RMS)误差值仅为0.055 4 μm，跟踪控制精度可达到10-8m。因此，相比于开环控制、前馈控制及PI反馈控制，复合控制算法能够基本消除压电陶瓷的迟滞非线性，同时具有很好的轨迹跟踪性能。

[1]OUYANG P R， ZHANG W J， MADAN M，etal.. Overview of the development of a visual based automated bio micro-manipulation system [J].Mechatronics， 2007， 17: 578-588.

[2]LIU Y， LI J， HU X，etal.. Modeling and control of piezoelectric inertia-friction actuators: review and future research directions [J].MechanicalScience， 2015， 6: 95-107.

[3]范伟， 林瑜阳， 李钟慎. 压电陶瓷驱动器的迟滞特性[J]. 光学 精密工程，2016， 24(5).

FAN W， LIN Y Y， LI ZH SH. Hysteresis characteristics of piezoelectric ceramic actuators [J].Opt.PrecisionEng.， 2016， 24(5).(in Chinese)

[4]MAIN J A， GARCIA E， NEWTON D V. Precision position control of piezoelectric actuators using charge feedback [J].JournalofGuidanceControlandDynamic， 1995，18:1068-1073.

[5]LIEN S， MIN S. Precision tracking of a piezo-driven stage by charge feedback control [J].PrecisionEngineering， 2013， 37: 793-804.

[6]LIN CH J， LIN P T. Tracking control of a biaxial piezo-actuated positioning stage using generalized Duhem model [J].ComputersandMathematicswithApplications， 2012， 64: 766-787.

[7]CAO Y，CHEN， X B. A survey of modeling and control issues for piezo-electric actuators [J].JournalofDynamicSystems，Measurement，andControl， 2015， 137(1).

[8]XIAO S， LI Y. Dynamic compensation andH∞ control for piezoelectric actuators based on the inverse Bouc-Wen mode [J].RoboticsandcomputerIntegratedManufacturing， 2014， 30: 47-54.

[9]王耿，官春林，张小军，等. 应变式微型精密压电驱动器的一体化设计及其PID控制[J]. 光学 精密工程， 2013， 21(3):709-716.

WANG G， GUAN C L， ZHANG X J，etal.. Design and control of miniature piezoelectric actuator based on strain gauge sensor [J].Opt.PrecisionEng.， 2013， 21(3):709-716. (in Chinese)

[10]LI Y M， XU Q S. Adaptive sliding mode control with perturbation estimation and pid sliding surface for motion tracking of a piezo-driven micromanipulator [J].IEEETransactionsonControlSystemsTechnology， 2010， 18(4):798-810.

[11]LIN C Y， CHEN P Y. Precision tracking control of a biaxial piezo stage using repetitive control and double feedforward compensation [J].Mechatronic，2011， 21:239-249.

[12]MA L， LI W， WANG Q，etal.. Identification of the bouc-wen hysteresis model for piezoelectric actuated micro/nano electromechanical system [J].JournalofComputationalandTheoreticalNano-science， 2013， 10(4).

[13]李华丰， 赵新丽. 应变反馈式压电陶瓷微位移驱动器的研制[J]. 计测技术， 2005， 25(4):19-20.

LI H F， ZHAO X L. Piezo actuators with strain gage sensors [J].MeasurementTechnology， 2005， 25(4):19-20. (in Chinese)

[14]王代华， 朱伟. WTYD型压电陶瓷微位移器的迟滞特性建模与实验验证[J]. 光学 精密工程，2010， 18(1):205-211.

WANG D H， ZHU W. Hysteretic modeling and experimental verification for WTYD type piezo ceramic micro-actuators [J].Opt.PrecisionEng.， 2010， 18(1):205-211. (in Chinese)

[15]CHEN X， LI Y. A modified PSO structure resulting in high exploration ability with convergence guaranteed [J].IEEETransactiononCybernetics， 2007， 37(5):1271-1289.

刘长利(1974-)，男，内蒙古包头人，博士，副教授，1998年于东北大学获得硕士学位，2004年于东北大学获得博士学位，主要从事机械系统动力学分析、机械电子方面的研究。E-mail: clliu@ecust.edu.cn

胡守柱(1990-)，男，江苏南京人，硕士研究生，2016年于华东理工大学获得硕士学位，主要从事压电陶瓷驱动系统、微动平台系统研究。E-mail：sozohu@163.com

(版权所有未经许可不得转载)

Feed-forward control of stack piezoelectric actuator

LIU Chang-li1， HU Shou-zhu1*， GUO Hai-lin1， WANG Xue-jun1，2， ZHANG Wen-jun1，3

(1.SchoolofMechanicalandPowerEngineering，EastChinaUniversityofScienceandTechnology，Shanghai200237，China;2.DepartmentofMechanicalEngineering，ColumbiaUniversity，NewYork10027，America;3.DepartmentofMechanicalEngineering，UniversityofSaskatchewan，Saskatoon250101，Canada)*Correspondingauthor，E-mail：sozohu@163.com

A novel inverse feedforward control algorithm was developed based on inverse Bouc-Wen feed-forward control and feedback control for improving the trajectory tracking performance of a Piezoelectric Actuator (PEA). A Bouc-Wen hysteresis dynamic modeling for the PEA was established， and system parameters of the Bouc-Wen model were identified by Particle Swarm Optimization (PSO) method. Then， a feed-forward compensation control method was proposed based on hysteresis Bouc-Wen model. Finally， the inverse feed-forward control method combining the PI feedback control with feed-forward control were proposed to control the piezoelectric actuator. An experimental platform was developed based on dSPACE system. The hysteresis experiment results show that the hysteresis error and relative linearity of the proposed method is almost zero and 96.5%， respectively. The trajectory tracking experimental results show that the maximum tracking error and RMS tracking error of the proposed method are 0.180 5 μm and 0.055 4 μm， respectively， obtaining the high tracking performance by 10-8m. As compared with open loop control， feedforward control， PI feedback control， the proposed inverse feedforward control algorithm compensates basically hysteresis nonlinearity of the PEAs and shows good trajectory tracking performance.

piezoelectric actuator; parameter identification; feed-forward control; trajectory tracking; Bouc-Wen model

2016-04-10；

2016-05-27.

国家自然科学基金资助项目(No.51175179)；中央高校基本科研业务费交叉与重大培育计划资助项目

1004-924X(2016)09-2248-07

TP273；TN384

A

10.3788/OPE.20162409.2248