EEMD降噪方法在飞机强度试验异响识别中的应用
韩 凯,冯建民,贺 谦,孙志强
(1.中国飞机强度研究所,全尺寸飞机结构静力/疲劳航空科技重点试验室,陕西 西安 710065;2.国防科技大学机电工程与自动化学院,湖南 长沙 410073)
EEMD降噪方法在飞机强度试验异响识别中的应用
韩 凯1,冯建民1,贺 谦1,孙志强2
(1.中国飞机强度研究所,全尺寸飞机结构静力/疲劳航空科技重点试验室,陕西 西安 710065;2.国防科技大学机电工程与自动化学院,湖南 长沙 410073)
针对飞机强度试验中异常信号被背景噪声淹没、提取信号特征困难这一问题,提出了结合相关系数的集合经验模态分解方法(EEMD)降噪方法。首先对信号进行EEMD降噪,然后根据相关系数筛选出用于重构信号的IMF分量,提取特征值,最后运用支持向量机进行分类辨识。通过与几种降噪法进行比较,结果表明,结合相关系数的EEMD降噪方法优于其它降噪方法,更适用于充满噪声的全尺寸飞机强度试验中。
集合经验模态分解方法;降噪;相关系数;特征提取;支持向量机
1 引 言
在飞机结构强度试验过程中,飞机结构和试验设备(杠杆、连接件等)可能会出现异常的响声。这些响声说明飞机结构或试验设备出现了损伤或是损伤的前兆。由于飞机结构和试验设备破坏形式复杂,位置多变,通过应变传感器提取出来的信息也不能准确反映试验件的损伤位置及状态,因此试验现场诊断确认十分困难。
在对飞机的损伤位置及状态进行试验现场诊断时,必须首先采集异响信号,进而对信号进行分析。但是在对信号进行分析之前,由于测试仪器、环境及人为因素的影响,采集到的异响信号往往含有较多的噪声。因此,为了能从采集信号中准确地提取出异响特征,必须先对信号进行降噪处理。
基于传统傅里叶变换的降噪方法存在保护信号边缘和抑制噪声之间的矛盾,难以正确识别信号中的噪声并加以去除,而基于小波变换的降噪方法,目前还没有一个选择合适小波类型的具体策略,且准确估计小波降噪时的阈值也存在一定的困难[1]。经验模态分解(Empirical Mode Decomposition,EMD)法[2],虽不依赖基函数,具有自适应的信号分解能力,但EMD存在频率混叠的问题,影响了其降噪的准确性。
为了抑制这种现象,Wu等[3]提出了集合经验模态分解方法(Ensemble Empirical Mode Decomposition,EEMD),利用高斯白噪声频率均匀分布消除先前的间断现象,从而解决了模态混叠的问题。此后有学者对EEMD进行了研究,取得了不错的成果。陈仁祥[4]对EEMD方法两个重要参数(白噪声幅值系数和总体平均次数)进行分析,提出了EEMD的自适应参数优化方法。李昌林[5]提出基于EEMD和Laplace小波相关滤波的滚动轴承诊断方法。唐贵基[6]将EEMD降噪方法与1.5维能量谱相结合获得滚动轴承故障特征频率信息,对轴承故障进行有效诊断。
为提高飞机结构强度试验中异响特征提取的准确性,减少人的主观经验的依赖,本文采用结合相关系数的EEMD方法对异响信号进行降噪,提取特征值,进行分类辨识,并将降噪效果和辨识结果与几种降噪法进行比较。结果表明,EEMD降噪方法优于其它降噪方法,更适用于充满噪声的全尺寸飞机强度试验中。
2 经验模态分解方法(EMD)
EMD方法具有自适应的信号分解能力,其目的是对一个非平稳信号进行平稳化处理。与小波变换和其它的时域分析方法相比,它有一个很大的优点,就是自适应,其根本原因在于这种变换是基于数据本身的一种分解,而不是基于事先设定好的基函数。EMD根据非平稳信号本身的特征时间尺度将其分解成有限个IMF和一个余项的和。
(1)
但EMD的缺点之一就是模态混叠,Wu等[3]认为在EMD分解过程中,采集的信号往往受到间断信号、噪声等的污染,使极值点的分布不均,影响极值点的选取,导致计算出来的相邻的两个IMF波形混叠,IMF的物理意义不清楚,错误地显示了信号的时频分布。
3 集合经验模态分解方法(EEMD)
3.1 EEMD原理
为了抑制传统EMD分解时的模态混叠现象,Wu等[3]提出基于EMD的改进方法EEMD,这是一种噪声辅助数据分析方法。EEMD的分解原理为:将高斯白噪声加入待分解信号来平滑极值点的不均匀分布,利用白噪声频谱的均匀分布使不同尺度的信号区域自动映射到与背景白噪声相关的适当尺度上,同时根据白噪声的零均值特性,对信号进行多次EMD分解,取IMF分量的均值作为最终结果。经过多次平均,使噪声相互抵消,抑制噪声的影响。EEMD的具体算法如下:
(1)在原始信号x(t)中分别加入N次均值为0、幅值标准差为常数的高斯白噪声Si(t),即:
xi(t)=x(t)+Si(t)
(2)
式中:i=1~N。
(2)对xi(t)分别进行EMD分解,得到K个IMF分量和一个余项ri(t),即:
(3)
(3)重复执行步骤(1)和(2),但每次加入的白噪声不同。
(4)利用不相关随机序列的统计均值为0的原理,将所得的对应IMF进行总体平均,消除多次加入高斯白噪声对真实IMF的影响,得到EEMD分解后的最终结果:
(4)
EEMD的两个重要参数:总体平均次数N和白噪声幅值系数。Wu等[3]建议,当N=100时,大部分情况下,噪声的幅值的标准差为信号的标准差的0.2倍。下面举例说明EEMD的优越性。
图1(a)为飞机结构铆钉剪断的断裂声的时域信号,图1(b)为飞机强度试验中油泵运行声的时域频域信号。将两种信号叠加组成为带噪信号(见图1(c))。带噪信号长度为20480点,时间1s。

(a)原信号的时域波形图
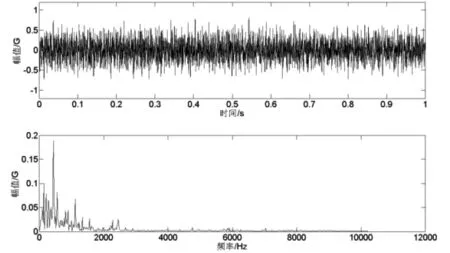
(b)噪声的时域和频谱图
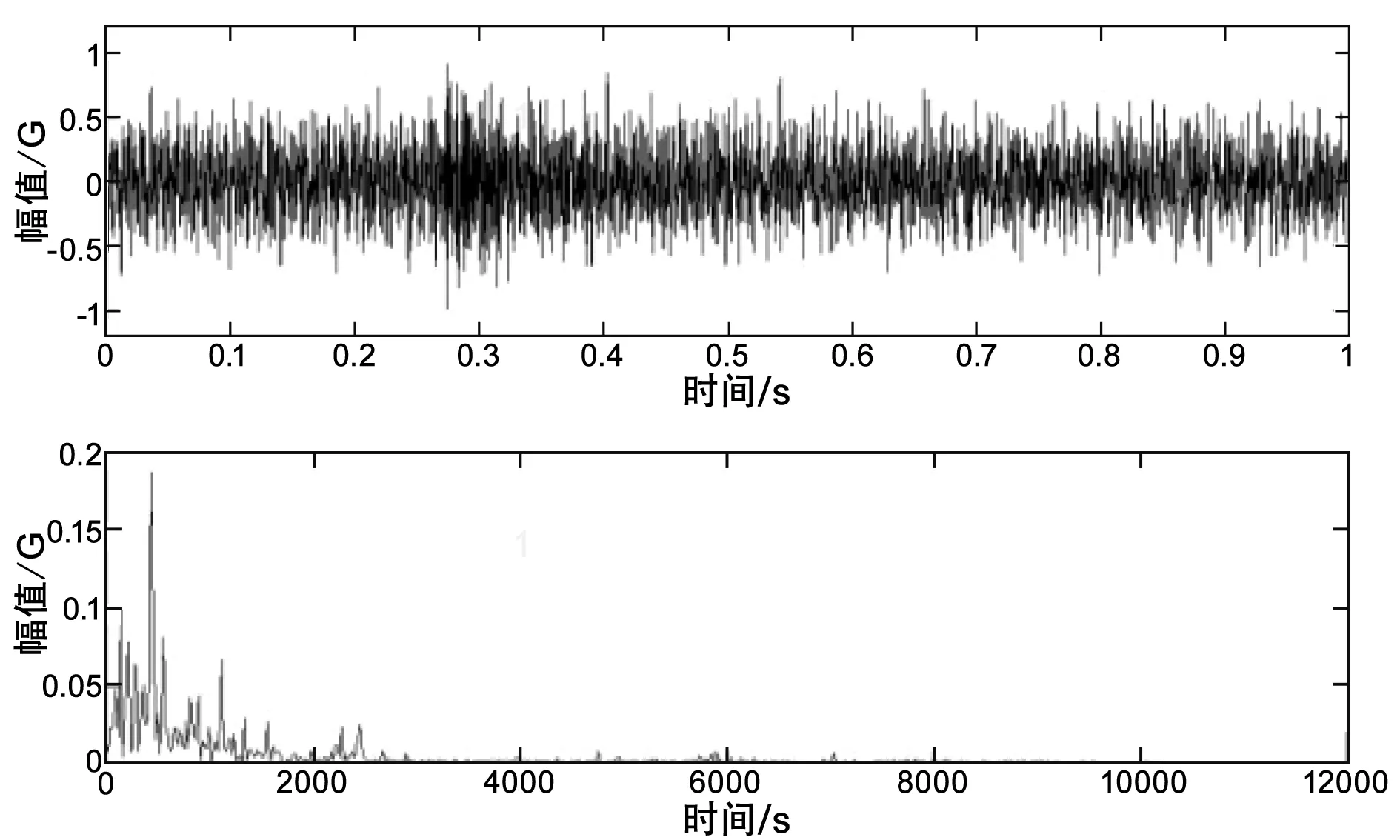
(c)带噪信号的时域和频谱图图1 测试信号及其组成
图2为带噪信号的EMD分解结果,其中,图2(a)为前6阶的IMF时域波形图,图2(b)为前6阶的IMF频谱图。从图中可以看出,虽然前2阶能得出是脉冲信号,但是已经被噪声所污染,频率分析中含有大量噪声的频率成分。

(a)EMD结果时域波形图
图3为带噪信号的EEMD分解结果,其中,图3(a)为前6阶的IMF时域波形图,图3(b)为前6阶的IMF频谱图。从时域和频域波形分析得出,第1阶IMF主要成分为叠加的噪声(见图1(b)),而第2和第3阶IMF代表了原信号的主要特征,只受到噪声少量污染。由此可得,原信号通过EEMD的分解,可以减少无关成分的干扰,有效地抑制模态混叠现象,能将噪声分解出来,使信号的类别特征更加突出。

(a)EEMD结果时域波形图

(b)EEMD结果频谱图图3 EEMD结果的时域频域波形图
3.2 EEMD降噪方法
原信号在EEMD运算过程中,由于存在分解、插值误差等影响因素,可能会产生误差。误差的不断累积会使信号分解结果中出现虚假分量,而虚假分量与原信号的相关性很小[7],因此可以通过相关系数来辨别虚假分量,其数学表达式为:
(5)

根据相关系数的特性,首先原信号进行EEMD运算,将得到的IMF分量,分别与原信号进行互相关,计算相关系数。设定一个阈值α,当相关系数小于阈值时,将其视为伪分量直接剔除,剩下的即为原信号的真实分量。
由上述内容,总结EEMD降噪方法步骤如下:
(1)对每一个样本声音信号进行EEMD分解,得到一组按照频率由高到低顺序排列的IMF分量。
(2)计算各分量与原信号的相关系数,设定阈值,剔除相关系数小于阈值的IMF分量。
(3)剩余的IMF分量进行重构,得到降噪后的信号。
4 声信号特征提取及识别
不同声音类型反映在信号中,频率分布不同,同时,信号的能量分布也不同。假设同一种类型的声音信号在不同频带的能量分布相同,即信号经EEMD分解所得的各IMF分量与信号的能量比变化不大。为了验证此假设,对异常声音信号进行EEMD分解,计算各个IMF的能量分布。
具体计算步骤如下:
(1)求出经过相关分析剔除伪分量后剩下的IMF分量的能量:
(6)
其中,Ai为幅值谱中的幅值,N为信号的长度,i=1,2,…,m。
(2)提取能量特征向量。由于能量值较大,为了便于分析和处理,对其进行归一化:
(7)
令:T=[E1/E,E2/E,…,Em/E]
T为归一化后的能量比,将其作为特征向量,输入支持向量机进行声音信号的分类与辨识。将得到的特征向量加入类别标识后,输入支持向量机进行训练,得到分类模型。然后采集飞机强度试验中带噪的异响信号作为测试信号,将测试信号通过分类模型进行分类验证。
5 工程应用分析
为了检验本文的降噪效果和类型辨识结果,现采用试验实测信号进行分析。设计标准试验件,在试验机上进行破坏试验,制造样本声音信号。在试验机四周,距声源不同距离布置12个B&K传声器,采集声音作为训练样本。其中,声音信号采集频率为20480Hz,声音信号采集精度为16bit。图4为铆钉结构试验件和试验现场。

图4 试验件及试验现场
对3种声音信号分别采样,作为原信号。对原信号进行EEMD分解,由EEMD的分解特性可知,分解得到的各层IMF从高到低频率依次衰减,其中第1阶主要为噪声信号,主要的声音特征信息集中在前几阶IMF分量中。本文取前2~6阶IMF分量,对3种声音信号的IMF分量分别求取其能量分布,并进行归一化处理,形成特征向量矩阵。将提取出来的特征向量输入到支持向量机中进行训练,形成分类模型。
为了对比各种方法的降噪效果,特引入信噪比和均方误差作为指标参数。各参数的定义如式(8)、式(9)所示。
(1)均方误差
(8)

(2)信噪比
(9)
5.1 不同方法降噪效果比较
为了对比不同方法对带噪信号的降噪效果,将飞机强度试验中油泵运行声作为噪声混入原信号中,形成带噪信号,分别采用维纳滤波、EMD降噪、EEMD降噪和结合相关系数的EEMD降噪方法对带噪信号进行降噪处理。降噪效果指标参数见表1,图5为原始信号与叠加噪声信号的时域图。

图5 原始信号与带噪信号的时域波形比较

SNRRSM原带噪信号-14.75090.2285维纳滤波降噪0.44860.0397EMD降噪-1.58820.0502EEMD降噪-1.47150.0495结合相关系数EEMD降噪1.53200.0351
由表1可以看出,维纳滤波和结合相关系数的EEMD降噪方法的降噪结果优于其他降噪方法。与EMD方法相比,EEMD降噪方法可以有效抑制相邻的IMF模态混叠现象,能清楚地分辨其频率的成分,从而取得比EMD降噪方法好的效果。图6为使用结合相关系数的EEMD降噪方法降噪后的时域图形。

图6 结合相关系数的EEMD降噪方法降噪后的信号时域图形
5.2 辨识结果比较
为了比较不同降噪方法对信号类型识别精度影响,取60组铆钉破坏声叠加油泵运行声作为测试样本,分别应用5.1节中所述的降噪方法进行降噪,然后按照4节中涉及的方法进行声信号特征提取,最后输入支持向量机进行识别,辨识结果见表2。

表2 声音信号类型预测结果
从表2可以得出,使用结合相关系数的EEMD降噪方法的信号辨识精度最高,而使用维纳滤波降噪方法虽然降噪效果也很好,但是辨识精度却很低,只有71.6%,分析原因是维纳滤波法将部分原信号剔除,使信号频率能量分布改变,造成信号失真,影响辨识精度。
6 结 论
本文利用一种结合相关系数的EEMD降噪方法对异响信号进行降噪,提取特征值,进行分类辨识,并将降噪效果和辨识结果与几种降噪法进行比较,通过分析,得出如下结论:
(1)结合相关系数的EEMD滤波方法具有自适应性,能有效去除信号中的噪声,提高信噪比,提高辨识精度。
(2)结合相关系数的EEMD滤波方法可以有效地抑制IMF分量频率混叠,避免相邻的两个IMF波形互相影响。
(3)采用相关系数这一标准对EEMD运算结果进行筛选,可以有效筛选出用于重构信号的IMF分量。
(4)结合相关系数的EEMD降噪方法优于本文中其它降噪方法,更适用于充满噪声的全尺寸飞机强度试验中。
[1]唐贵基,张文德,林琳.一种基于优化阈值函数的整体强化分解模型改进降噪方法[J].科学技术与工程,2014,14(16):134-138.
[2]Huang N E, Shen Z, Long S R. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Froc.R.Soc.Lond.A,1998,454:903-995.[3]Wu Z H, Huang N E.. Ensemble empirical mode decomposition:a noise assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1):1-41.
[4]陈仁祥,汤宝平,杨黎霞,等.自适应参数优化EEMD机械故障特征提取方法[J].振动、测试与诊断,2014,34(6):1065-1170.
[5]李昌林,孔凡让,黄伟国,等.基于EEMD和Laplace小波和滚动轴承故障诊断[J].振动与冲击,2014,33(3):63-69.
[6]唐贵基,王晓龙.基于EEMD降噪和1.5维能量谱的滚动轴承故障诊断研究[J].振动与冲击,2014,33(1):6-10.
[7]苏文胜,王奉涛,张志新,等.EMD降噪和谱峭度法在滚动轴承早期故障诊断中的应用[J].振动与冲击,2010,29(3):18-21.
Application of EEMD Noise Reduction Method to Abnormal Sound Recognition of Aircraft Strength Test
Han Kai1, Feng Jianmin1, He Qian1, Sun Zhiqiang2
(1.Aircraft Strength Research Institute of China, Key Laboratory of Full Scale Aircraft Structure Static and Fatigue Test, Xi′an 710065, Shaanxi, China;2.College of Mechatronics Engineering and Automation, National University of Defense Technology, Changsha 410073, Hunan, China)
Aiming at the problems that the abnormal sound signal is buried in the background noises in aircraft strength test and it is difficult to obtain available abnormal sound signal feature, the noise reduction method based on ensemble empirical mode decomposition (EEMD) and correlation coefficient is proposed. Firstly, abnormal sound signal is decomposed by EEMD and a set of intrinsic mode function components are obtained. Filtering the components according to the correlation coefficient, the selected IMF components are used to reconstruct the signal. Lastly, energy feature extracted from a number of IMFs could serve as input vectors of support vector machine. Practical examples show that the method has obvious advantages compared with other noise reduction methods and can be used in aircraft strength test with the strong background noise.
ensemble empirical mode decomposition; noise reduction; correlation coefficient; feature extraction; support vector machine
2016-08-10
韩 凯(1985-),硕士研究生,研究方向:飞机强度试验技术研究。
冯建民(1966-),博士,研究员,研究方向:飞机强度试验技术研究。
航空基金(20150981006,20140937001)资助。
V216.5+4
B
10.3969/j.issn.1674-3407.2016.03.003

