平均断面法在计算道路弯曲处土方的缺陷及改进

谢国平，谢 聪

（蓬安县土地勘测设计室，四川 蓬安 637800）

平均断面法在计算道路弯曲处土方的缺陷及改进

谢国平，谢 聪

（蓬安县土地勘测设计室，四川 蓬安 637800）

在道路弯曲处的土方计算由于相邻断面之间不平行，断面间几何中心水平投影距离不一样，若直接采用平均断面法计算土方，会影响土方量计算的准确性。针对这种情况，本文建议采用平均断面法的改进型来计算道路弯曲处的土方，平均断面法改进型相邻断面间距以几何中心投影间距代替相邻垂直断面之间的道路中心距离。通过对工程实例中的三种土方计算方法比较，可知平均断面法改进型在道路弯曲处计算土方具有更高的精度。

平均断面法；断面的几何中心；半挖半填断面；模拟三角形；DTM两期土方

引 言

在铁路、公路等线形工程的规划设计和工程量结算中，断面法对带状工程的土方量计算尤其适用，因此，测量设计人员常常采用平均断面法进行填挖土方量计算。然而在道路弯曲处由于相邻断面之间不平行，且大多数断面属半挖半填断面样式，半挖和半填断面几何中心水平投影距离不一样，若仍然采用平均断面法计算土方，显然会影响土方量计算的准确性。针对这种情况，本文建议采用平均断面法的改进型来计算道路弯曲处的土方，很好地解决了这一问题。

1 平均断面法的理论公式

在线形工程中，以垂直于道路中心线的方式，根据地形要求以 10～30 m为间距设置多个垂直断面，一般垂直断面之间的间距取相同的数值，直线段的垂直断面相互平行，曲线段垂直断面指向圆心且相互之间不平行。平均断面法是假定相邻断面S1、S2间为一棱柱体，其高为两相邻断面的间距D，则相邻断面间土石方数量V按公式（1）来近似计算。断面法土方量的计算一般分两步，首先计算填方或挖方的断面面积，然后再根据两横断面的平均面积乘以两横断面之间的间距算得填挖土方量。即：

式中：V为两个相邻垂直断面之间的挖方或者填方的体积；S1、S2分别为两个相邻垂直断面的面积；D为两个相邻垂直断面之间的间距。

平均断面法的特点是比较实用且简便迅速，但精度较差。该法只有当相邻面积 S1和 S2相差不大时才较准确，当S1和 S2相差较大时，计算结果偏大。尤其是当相邻断面是一填一挖时，断面间实为一棱锥体，这时仍取平均面积来计算，计算所得的工程量要比实际工程量偏大。为此，长沙理工大学唐平英教授在平均断面法的基础上加以改进，提出了填挖土方量计算的精确公式，即：

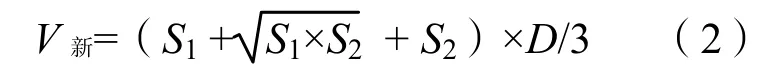
公式（2）在两相邻断面填、挖方面积相差较大计算土方量时，较公式1精确，在相邻横断面面积接近时，具有与公式（1）相同的精度。

2 平均断面法的缺陷及改进

在道路方量计算中，平均断面法公式只需要知道两端横断面的面积和相邻垂直断面之间的间距就可以计算出相邻断面之间的土方量，通常相邻垂直断面之间的间距是以相邻断面间的道路中心距离来代替的。在道路直线段由于相邻断面之间相互平行，其相邻垂直断面之间的间距等于相邻垂直断面之间的道路中心距离；但在道路弯曲处由于相邻断面之间不平行（如图1），如半挖半填断面样式，由于内部断面属性不同，分别由挖方和填方断面组成，其半挖和半填断面几何中心不同，断面间几何中心水平投影距离就不一样，其断面间的几何中心间距与相邻断面间的道路中心距离因此不相等，这就给道路弯曲处用平均断面法计算方量带来较大误差。

图1 道路弯曲处半挖断面间的几何中心水平投影

在道路弯曲处的半挖半填样式中，平均断面法中的两个相邻垂直断面之间的道路中心距离 D不能很好地反映半挖半填断面间距实际情况（如图 1所示）。基于上述原因，提出对平均断面法在道路弯曲处的土方计算方式加以改进，平均断面法改进型采用相邻断面间的几何中心投影间距L代替相邻垂直断面之间的道路中心距离D，然后按公式（2）计算断面间方量。显然这种改进后的方量计算方式具有更高的精度，而保证这种改进方法是否实用的关键就在于能否快速求出相邻断面间的几何中心投影间距。

3 断面的几何中心及水平投影间距

求出相邻断面间的几何中心间距就要先找出不规则断面的几何中心位置。在数学方法中，质心就是质量相对于位置的加权平均，即质量相对于位置的加权和再除以总质量。不规则断面的几何中心位置就是断面本身的质心，按此方法找出不规则断面的几何中心位置虽然科学，但在实际工作中计算量较大，且使用极其不便，不利于土方量的计算效率。

在道路方量计算中，为了更快更好地找出不规则断面的几何中心位置，我们将不规则断面模拟成规则几何形状。根据不同的道路断面类型，我们将不规则断面分为3种情况：全挖、全填、半挖半填。

图2 全挖断面样式

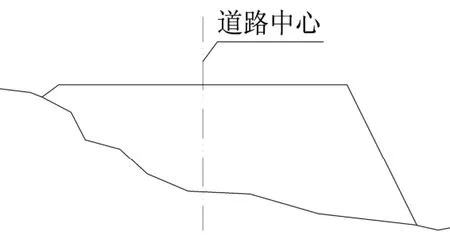
图3 全填断面样式

由图2、图3可知，全挖、全填由于内部断面属性相同，形状近似梯形，且总体对称，断面的几何中心水平投影与道路中心几乎一致，断面间的几何中心水平投影间距与断面间道路中心距离近乎相等。

半挖半填断面样式中，其几何形状极其复杂，由于挖填方单价不同，挖方量的准确性尤其重要，在山地地形中，半挖断面往往呈阶梯状，可将半挖断面模拟成具有规则形状的三角形。如图4半挖断面，不论其外形如何，都可以将挖方断面模拟成面积相等形状近似的三角形（图4中三角形ABC），称之为模拟三角形，用模拟三角形的几何中心来代替不规则半挖断面几何中心。由数学可知模拟三角形的几何中心为三边垂直平分线的交点，其几何中心水平投影为三角形BC的中点。

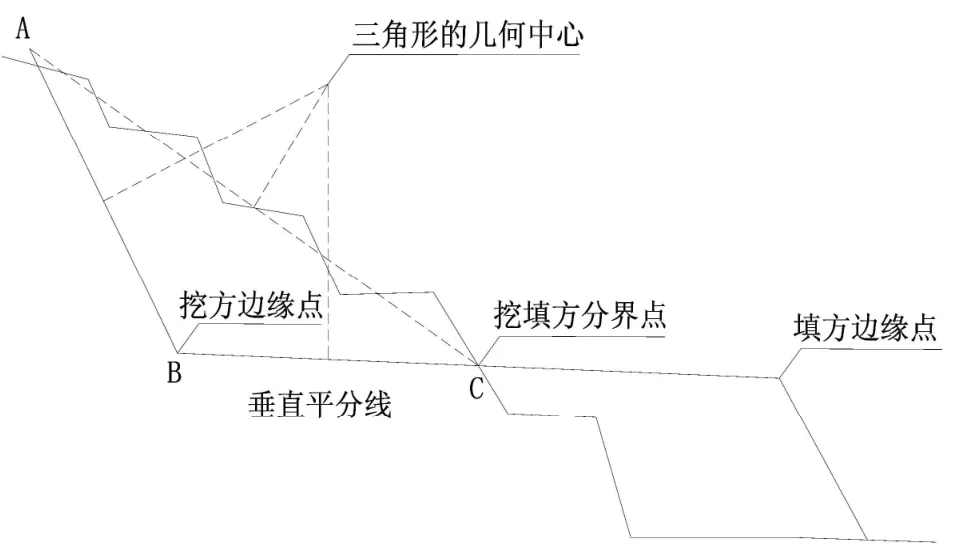
图4 半挖半填断面样式

如图 4，半挖半填断面样式挖方断面几何中心水平投影为模拟三角形的底边中点，即挖填方分界点到挖方边缘点的中点，半挖断面几何中心投影间距等于相邻模拟三角形的底边中点投影间距（见图1）；为了保证断面间总距离不变，相应地，半填断面几何中心投影间距等于两倍相邻断面间道路中心距离与相邻断面模拟三角形的底边中点投影间距之差，即：

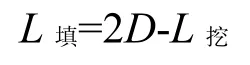
其中：L填为两个相邻半填断面间的几何中心间距；L挖为两个相邻半挖断面间的几何中心间距。

4 工程实例

我们以蓬安县抚琴南路某弯曲处土方量计算为例，来探讨道路弯曲处半挖半填断面样式利用平均断面法改进型计算道路弯曲处土方的适用性。抚琴南路某弯曲处长度约150 m，路面宽40 m，圆曲线半径150 m，属典型的半挖半填断面样式。

在该工程的野外测量数据采集时，为了保证高程数据对地形的表达更加完整，土方测量时着重加强了对地形特征点数据的采集工作，包括地形变化点、特殊地貌点、变坡点、坎上坎下、沟渠、陡崖上下等明显点位的采集。为了保证土方量的计算精度，一方面要求提高测量精度，另一方面限制测量采点密度在5 m以内，保证野外测量数据采集密度完全符合DTM法对密度的要求。

在内业处理工作中，主要是对地形变化区域的高程点进行添加和剔除，对地形高程数据密集程度不够且不宜采集的地形变化点进行数据加密，对GPS数据采集的浮动点、飞点、高程错误点等不适宜参与土方计算的高程点进行剔除。在完成数据处理之后，保存好原始地形结果数据，以便进行下一步数据提取和土方计算操作。

下面以3种土方计算方法为例来进行比较。

1）平均断面法计算道路弯曲处土方（断面间采用道路中心距离）

为了计算方便和保证土方计算精度，道路路面设计采用水平面，挖方边坡按1：0.3设计，填方边坡按1：0.5设计，道路断面间距10 m左右，采用断面15个，断面间道路中心距离总长为142.62 m，断面采样间距要求小于野外测量采点密度5 m，实际采用2 m。采用平均断面法计算公式（2）计算该处土方，计算结果为：挖方 9 686 m3，填方24 748 m3。

2）平均断面法改进型计算道路弯曲处土方（断面间采用几何中心水平投影距离）

利用南方CASS7.1软件，根据各断面图的挖填方分界点与道路中心的相互关系，在设计地形图中标示出横断面线、各断面间的挖填方分界线以及设计路面边缘线，再据此求出各断面间几何中心水平投影距离，得到半挖断面间几何中心水平投影距离总长为135.5 m，比断面间道路中心距离总长减少7.12 m，半填断面间几何中心水平投影距离总长为149.74 m，比断面间道路中心距离总长增长7.12 m。采用平均断面法改进型计算该处土方，计算结果为：挖方9 250 m3，填方26 186 m3。

3）用南方CASS7.1中的DTM两期土方计算道路弯曲处土方

因为DTM法直接利用外业所采集的地形碎部点、特征点进行三角构网，直接利用原始数据作为网格结点，不改变原始数据和精度；三角网中的点和线的分布密度和结构与地表的特征相吻合，能很好地适应复杂地形，与实际地形情况模拟相当契合，因此DTM法计算土方量是精度较高的。为了更好地比较上述两种土方计算方法的优劣，我们采用DTM法的两期土方计算方法来验证，以保证土方量计算的准确性。

在 CASS7.1中以道路断面边坡边界的连线作为挖填方计算范围线，利用原始地形数据生成三角网，根据实际地形调整三角网，最终建立与实际地形相吻合的数字地面模型，将原始地形数据生成的三角网结果输出作为一期三角网保存。然后再构建二期三角网，二期三角网的设计平面范围边线与一期三角网挖填方计算范围线相一致，设计面 DTM主要从 15个道路断面中设计线地形变化处获取三维坐标数据：其平面坐标主要是根据各断面图的设计线地形变化处与道路中心相互关系求得，高程数据主要是根据各断面图直接获取，在CASS7.1中输入命令“G”后捕捉挖填方计算范围线、道路设计边线等设计面变化的平面位置，再用手工直接输入各设计面变化处的高程，与野外数据采集一样有坡、坎的，坡顶、坡底、坎上、坎下要相对应的加点，保证足够的密度，将所计算的点逐一追加到二期数据文件中保存，然后生成三角网建立DTM模型并调整保存为二期三角网。利用CASS7.1中DTM两期土方计算方法，计算得挖方9 003 m3，填方26 930 m3。

5 结 语

从上述实例计算结果可知：平均断面法改进型和 DTM两期土方计算道路弯曲处土方结果最接近，两种方法的挖填方量差值均小于3 %，计算较为精确；而平均断面法与DTM两期土方比较，其挖填方量差值均大于7.5 %，计算误差较大；同时平均断面法的计算结果使挖方量变大，填方量变小，从而影响土方量计算的准确性。显然，在道路弯曲处的土方计算，平均断面法改进型比平均断面法精度更高。

因此建议将道路弯曲处的土方量计算分成两种情况，全挖全填断面样式可直接采用平均断面法计算，断面间距离采用道路中心距离；半挖半填断面样式，采用平均断面法的改进型计算，半挖断面间距离采用几何中心水平投影距离较为适宜。由于平均断面法改进型也只需要知道相邻断面面积，而仅在弯曲道路的半挖半填断面样式中将半挖断面间道路中心距离改为几何中心水平投影距离，因此它与平均断面法公式同样简单。当然平均断面法改进型对其它线形工程弯道处的土方计算同样适用。

［1］唐平英.断面法土方量计算公式的精度［J］.港工技术，1998.

［2］粟晟，欧陆.南方CASS计算两期间土方与方格网法土方计算相结合准确计算土方量［J］.中国井矿盐，2013.

［3］张正禄.工程测量学［M］.武汉：武汉大学出版社.

Defect of Average Section Method in Calculation of Earthwork at Road Bend
and Improvement Measures

Xie Guoping，Xie Cong
（Land Surveying and Design Office of Peng'an County，Peng'an Sichuan 637800，China）

Since the adjacent sections are unparallel each other and their geometric-centre horizontal projection distances are different，the application of average section method will affect the calculation accuracy of earthwork at road bend.In the case，an improved average section method is proposed to calculate the earthwork at road bend.The road center distance between two adjacent vertical sections is replaced by the geometric center projection distance.The comparison of three earthwork calculation methods shows higher precision of the improved average section method in the calculation of earthwork at road bend.

average section method； geometric center of cross section； excavate-and-fill section； analog triangle；DTM two-period earthwork

U461.1+11

A

1004-9592（2016）05-0069-04

10.16403/j.cnki.ggjs20160518

2016-02-17

谢国平（1970-），男，工程师，主要从事工程测绘及土地规划工作。