S-分布时滞的随机Hopfield神经网络的稳定性❋

孙小淇， 王林山

(1.中国海洋大学信息科学与工程学院，山东 青岛 266100； 2.中国海洋大学数学科学学院，山东 青岛 266100)



S-分布时滞的随机Hopfield神经网络的稳定性❋

孙小淇1， 王林山2❋❋

(1.中国海洋大学信息科学与工程学院，山东 青岛 266100； 2.中国海洋大学数学科学学院，山东 青岛 266100)

研究一类具有S-分布时滞的随机Hopfield神经网络的稳定性问题。通过构造随机Lyapunov泛函与随机分析技巧相结合的方法得到了实用有效的判别准则.具有S-分布时滞的Hopfield神经网络解决了具有离散时滞的Hopfield神经网络和具有连续分布时滞的Hopfield神经网络不能相互包含的问题。且本文在已有文献的系统模型中加入了随机干扰项，证明了该随机Hopfield神经网络全局解的存在唯一性及其全局均方鲁棒指数稳定性，使其具有更广泛的实际应用价值，推广了相关文献中的结果。

神经网络； S-分布时滞； 全局均方鲁棒指数稳定性

引用格式：孙小淇，王林山. S-分布时滞的随机Hopfield神经网络的稳定性[J].中国海洋大学学报(自然科学版), 2016, 46(10):139-142.

SUN Xiao-Qi， WANG Lin-Shan. Stability of stochastic Hopfield neural network with S-type distributed delays [J].Periodical of Ocean University of China, 2016, 46(10):139-142.

1982年美国生物物理学家J. Hopfield提出了具有联想记忆功能，能量定律和动力方程等特点并且可以在集成电路上实现的Hopfield神经网络模型[1]，这些特点奠定了这种网络的辉煌前景。此后，众多学者对Hopfield神经网络进行了深入的研究，研究成果增长迅速[2]。特别是关于网络的稳定性研究引起了人们的关注[3-7]。文献[8-10]运用Lyapunov函数与Razumikhin条件相结的方法研究了随机时滞Hopfield神经网络的指数稳定性，给出了依赖于时滞的稳定性判据。具有离散时滞和分布时滞的神经网络是相互独立的，而具有S-分布时滞的神经网络却蕴含了二者。文献[11-13]研究了具有S-分布时滞的Hopfield神经网络的稳定性，随后关于这种网络的稳定性的研究文献大量涌现。但是据作者所知，关于S-分布时滞的随机Hopfield神经网络稳定性研究相对较少，其原因是随机扰动的引入，给研究这类网络带来了较大的困难。本文运用随机Lyapunov泛函和随机分析技巧相结合的方法，研究了S-分布时滞随机Hopfield神经网络的全局均方鲁棒指数稳定性，给出了易于验证的稳定性判据。推广了相关文献中的结果。

1　主要结果

考虑如下S-分布时滞随机Hopfield神经网络

(1)

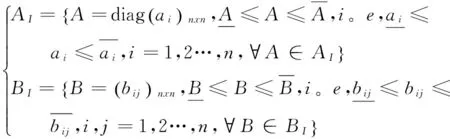
(2)

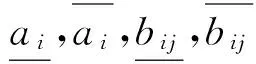
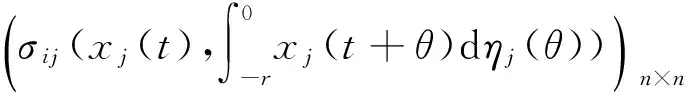
(3)

初始条件φ=(φ1(t),φ2(t),…,φn)T:[-r,0]→Rn是F0可测的，且右连续。

引理1[14]考虑如下随机泛函微分方程

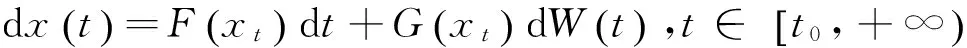
(4)

若满足下列条件：

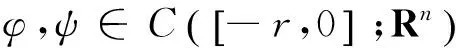
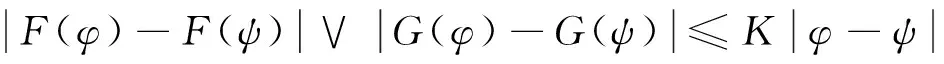
(5)

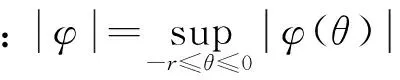
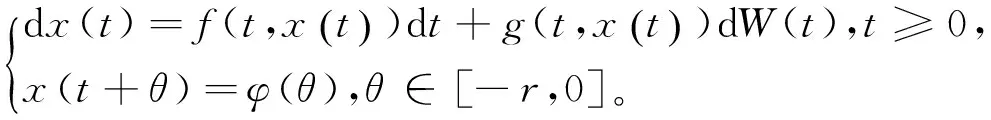
(6)

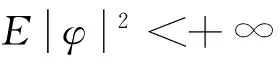
dV(t,φ)=(Vt(t,φ(0))+Vx(t,φ(0))f(t,φ)+

LV(t,φ)dt+Vx(t,φ(0))g(t,φ)dWt。

(7)

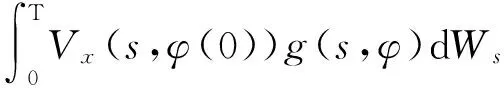
(8)

其中

LV(t,φ)=Vt(t,φ(0))+Vx(t,φ(0))f(t,φ)+

(9)

定义1如果存在正常数P，β，使得系统(1)存在满足条件(2)的解，且这个解满足：

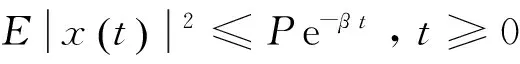
(10)

则称系统(1)是全局均方鲁棒指数稳定的。

定理1假设下列条件成立：

(A1)设 fj(0)=σij(0,0)=0且存在常数lj>0，cij>0,dij>0,i,j=1,2，…，n，使得对任意ν,μ,x,y∈R，有

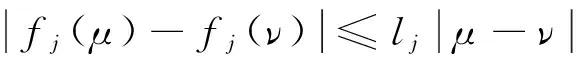
(11)

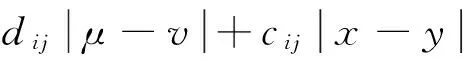
(12)

(A2)下列不等式成立

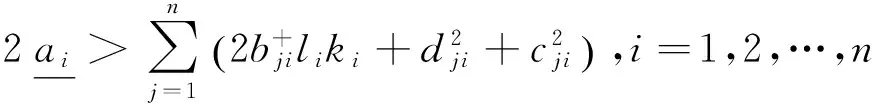
(13)

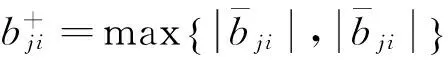
则满足条件(A1)～(A2)的系统(1)存在唯一的全局解，且系统(1)是均方鲁棒指数稳定的。

证明

Ⅰ系统(1)存在唯一全局解

令

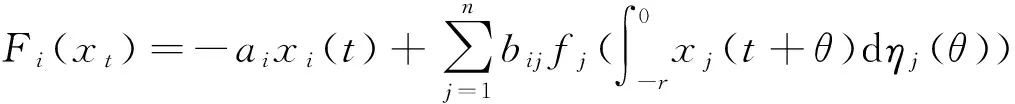
(14)

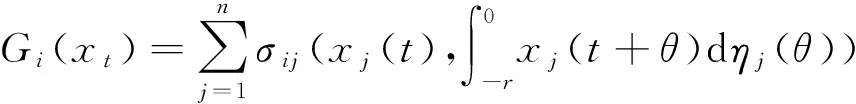
(15)

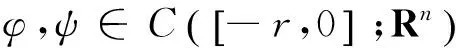
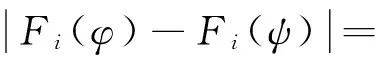
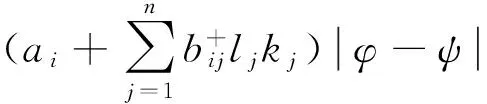
(16)

从而

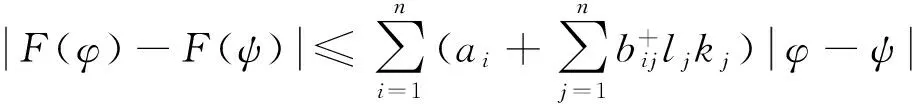
(17)

同理由(A1)得

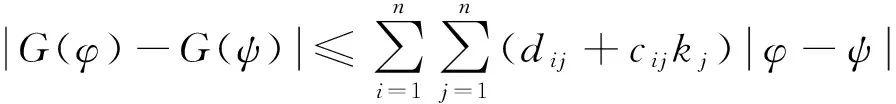
(18)

令

(19)

则 (5)式成立。从而由引理 1 知，则系统(1)存在唯一连续的全局解x(t),t≥0。

Ⅱ 系统(1)均方鲁棒指数稳定

定义

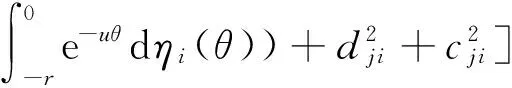
(20)

由(A2)可知

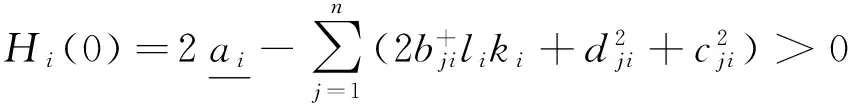
(21)

由H(u)在(0,+∞)上连续，且当u→+∞时，H(u)→-∞。故存在u*∈[0,+∞)，满足

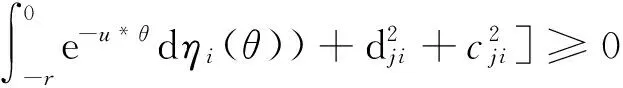
(22)

定义Lyapunov泛函

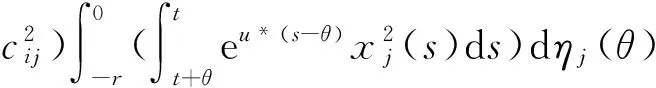
(23)

由(2), (7), (23)和 (A1)得

θ)dηj(θ))dwj(t)≤

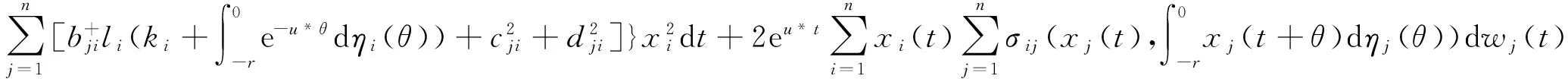
(24)

由(8)和 (22)可知

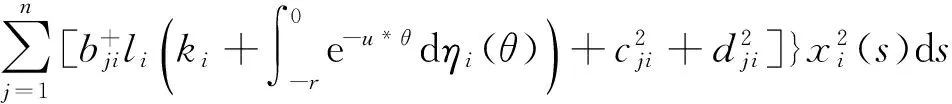
θ)dηj(θ))dwj(s)≤

(25)

上式两端取数学期望得

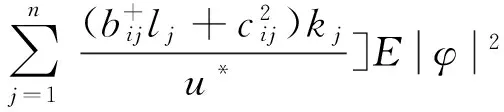
即

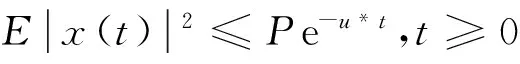
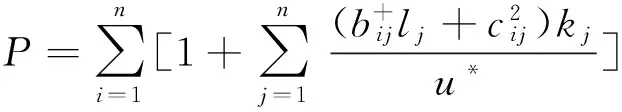
注1 如果扩散系数σij=0,i,j=1,2,…,n，则系统(1)转化为文献[2]中第三章研究的系统，因此文献[2] 第三章研究问题是本文的特例。

实例

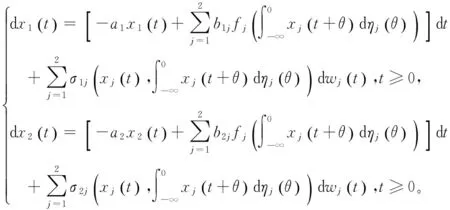
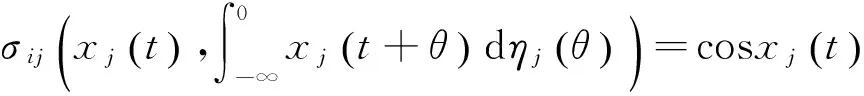
kj=1。j=1,2。则显然满足定理中条件(A1)，且可取

l1=l2=d11=d22=c11=c22=1,

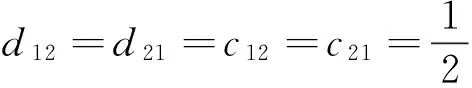
则有

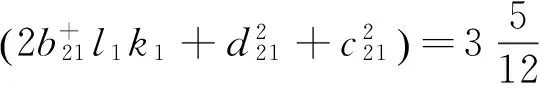
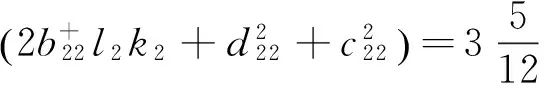
满足定理中条件(A2)，因此该系统是均方鲁棒均方指数稳定的。

[1]Hopfield J J. Neurons with graded response have collective computational properties like those of two-state neurons [J]. Proceedings of the national academy of sciences, 1984, 81(10): 3088-3092.

[2]王林山. 时滞递归神经网络(Delayed recurrent neural network)[M]. 北京： 科学出版社， 2008.

Wang L.Delayed Recurrent Neural Network[M]. Beijing： Science Press, 2008.

[3]Forti M, Tesi A. New conditions for global stability of neural networks with application to linear and quadratic programming problems [J]. Circuits and Systems I: Fundamental Theory and Applications, IEEE Transactions on, 1995, 42(7): 354-366.

[4]Wan L, Sun J. Mean square exponential stability of stochastic delayed Hopfield neural networks [J]. Physics Letters A, 2005, 343(4): 306-318.

[5]Wang Z, Shu H, Fang J, et al. Robust stability for stochastic Hopfield neural networks with time delays [J]. Nonlinear Analysis: Real World Applications, 2006, 7(5): 1119-1128.

[6]Duan S, Hu W, Li C, et al. Exponential Stability of Discrete-Time Delayed Hopfield Neural Networks with Stochastic Perturbations and Impulses [J]. Results in Mathematics, 2012, 62(1-2): 73-87.

[7]Pradeep C, Vinodkumar A, Rakkiyappan R. Delay-dependent exponential stability results for uncertain stochastic Hopfield neural networks with interval time-varying delays [J]. Arabian Journal of Mathematics, 2012, 1(2): 227-239.

[8]沈轶, 廖晓昕. Hopfield 型时滞神经网络的指数稳定性[J]. 数学物理学报: A 辑, 1999, 19(2): 211-218.

Shen Y, Liao X.Exponential Stability of Hopfield Neural Networks[J].Acta Mathematica Scientia, 1999, 19(2)： 211-218.

[9]沈轶, 廖晓昕. 非线性随机时滞系统族的鲁棒稳定性[J]. 自动化学报, 1999, 25(4): 537-542.

Shen Y,Liao X.Robust stability of a family of nonlinear stochastic delay systems[J].Acta Automatica Sinica, 1999, 25(4): 537-542.

[10]Wallis G. Stability criteria for unsupervised temporal association networks [J]. IEEE Transactions on Neural Networks, 2005, 16(2): 301.

[11]Wang L, Xu D. Global asymptotic stability of bidirectional associative memory neural networks with S-type distributed delays [J]. International Journal of Systems Science, 2002, 33(11): 869-877.

[12]Wang Y, Lu C, Ji G, et al. Global exponential stability of high-order Hopfield-type neural networks with S-type distributed time delays [J]. Communications in Nonlinear Science and Numerical Simulation, 2011, 16(8): 3319-3325.

[13]Zhang R J， Wang L S． Global exponential robust stability of interval cellular neural networks with S-type distributed delays[J]．Mathematical and Computer Modelling， 2009， 50： 380-385.

[14]Mao X R． Stochastic Differential Equation and Application (second edition)[M]． Chichester： Horwood Publishing， 2007.

AMS Subject Classifications：00A69； 03B30； 03C05

责任编辑陈呈超

Stability of Stochastic Hopfield Neural Network with S-Type Distributed Delays

SUN Xiao-Qi1， WANG Lin-Shan2

(1.College of Information Science and Engineering, Ocean University of China, Qingdao 266100， China; 2.School of Mathematical sciences, Ocean University of China, Qingdao 266100， China)

This paper is studied the stochastic Hopfield neural network with S-type distributed delays and investigated stability problems of this neural network. Some sufficient conditions on global robust exponential stability in mean square are established in this paper. The means are mainly constructing the suitable Lyapunov functional and applying the stochastic analysis techniques. Because the systems with discrete time delays and the systems with continuously distributed delays do not contain each other. However, S-distributed delays are introducted in stochastic neural network with time delays. It effectively solves the problem that discrete and distributed delays issues not included in the mutual. More even, the existence and uniqueness of solutions and the global robust exponential stability in mean square of the system are proved, which are promoted the results of the relevant literature. An example was given to show the correctnessof the conclusions.

neural networks； S-type distributed delays； global robust exponential stability in mean square

国家自然科学基金项目(11171374)； 山东省自然科学基金重点项目(ZR2011AZ001)资助

2014-10-12；

2015-06-12

孙小淇(1986-)，女，博士生。E-mail:sunxiaoqi@live.com.

❋❋通讯作者： E-mail：Wangls@ouc.edu.com

TP183

A

1672-5174(2016)10-139-04

10.16441/j.cnki.hdxb.20140231

Supported by National Natural Science Foundation of China(11171374)；Shandong Municipal Natural Science Foundation(ZR2011AZ001)