某火炮自动机高速机构的热-结构耦合效应仿真分析

戴涌，钱林方，吴晓金，徐亚栋

（1.南京理工大学机械工程学院，江苏南京210094；2.重庆望江工业有限公司军品研发中心，重庆400071）

某火炮自动机高速机构的热-结构耦合效应仿真分析

戴涌1，2，钱林方1，吴晓金2，徐亚栋1

（1.南京理工大学机械工程学院，江苏南京210094；2.重庆望江工业有限公司军品研发中心，重庆400071）

针对某高射速自动机在样机实弹射击时出现的周期性停射故障，应用热膨胀经典理论和有限元计算方法，对高射速自动机进行了热-结构耦合分析。结果表明：将结构尺寸作适当的调整，不仅能满足现阶段射速的要求，而且有进一步提高射速的空间。结构设计方案改进后的验证样机，经多轮实弹试验测试，没有出现周期性停射现象，故障得到解决。将热-结构耦合方法应用于工程实践，以期在解决类似故障和结构设计的分析方法上有所借鉴。

兵器科学与技术；自动机；有限元；热-结构耦合

0　引言

火炮自动机结构在受热状态下，不仅受外载荷产生的结构应力影响，还受到温度场产生的热应力影响，并可能导致结构功能失效或破坏，分析这些问题时，必须考虑温度场的变化对结构强度、刚度和承载能力的影响。如今，有很多方法可以来进行热-结构耦合分析，如有限元方法。该数值模拟方法结合实际试验所带来的最大好处是能够节约大量的研制成本，对武器系统的设计具有很好的指导作用。目前，热-结构耦合研究应用主要集中在航空航天领域，国内外相关研究报道也比较多［1-4］，而在常规武器装备设计方面的应用研究则较少。

传统火炮自动机结构设计过程中，一般不考虑热过程，通常情况下这样不会产生问题。但是任何材料都有不同程度的热胀冷缩现象［5］，尤其是对于运动配合受约束较多的机构在工作过程中，由热膨胀引起的故障日益突出，如某型装备在试验过程中出现的周期性停射故障。该装备的某连续高速运动机构由箱体、基体和前后衬套等零件组成，机构工作时在基体内产生高温高压气体，并以极高的频率消失和生成，基体和箱体固定不动，而前后衬套须在高温高压气体作用下完成往复运动以使整个机构完成预定的动作；当往复运动持续一段时间后，起初处于室温状态的箱体、基体和前后衬套的温度得到不同程度的升高，由于它们的温升变形量引起衬套的运动出现卡死，机构停止运动；间隔一段时间后，温度下降到临界点，卡滞消失，机构又恢复运动。此故障现象具有一定的周期性和原因不确定性，严重地影响了装备的正常运行，并对操作人员的人身安全造成极大的威胁，必须予以排除。

本文针对上述问题，采用有限分析方法先对结构进行热传导分析，得到结构内部的温度场分布；再进行结构分析，得到由温度产生的结构应力；最后通过分析反推结构设计时的公差配合关系。

1　结构热分析

结构热分析是求解温度场对结构中应力、应变和位移等物理参数的影响，即利用现有的技术方法，对处于某种温度载荷下的结构进行热应力和结构应力的耦合分析。对于热结构分析，在有限元方法中通常用顺序耦合分析，即先进行热分析求得结构的温度场，再进行结构分析。将热分析求得的温度场作为载荷加到结构分析中，求解结构中的应力分布。

在三维问题中，瞬态温度场的场变量φ（x，y，z，t）在直角坐标中应满足的微分方程为

式中:ρ为材料密度；c为材料比热容；t为时间；kx、ky、kz是材料沿着3个主方向的导热系数；Q=Q（x，y，z，t）是物体内部的热源密度。

求解瞬态温度场问题是求解在初始条件下，即在φ（x，y，z，t）=φ0（x，y，z）条件下，满足瞬态热传导方程及其边界条件的场函数φ，φ应是坐标与时间的函数。

针对上述三维问题中瞬态热传导微分方程和边界条件，建立起等效积分形式:

式中:w、w1、w2、w3是任意函数，按照伽辽金法选择任意函数，设Γ1上已经满足强制边界条件，则w1= 0，并且不失一般性，可以令

将（3）式代入（2）式中，并且对其中第一项中Ω内积分的第2～4项进行分部积分，则可得到（2）式等效积分的“弱”形式为

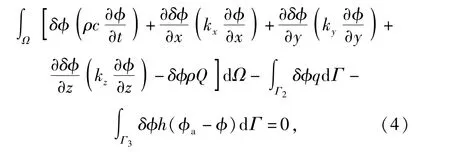
利用（4）式可以建立起瞬态温度场有限元的一般格式。首先将空间域离散为有限个单元体，在单个单元内温度可以用节点温度插值得到，即

式中:n为单元体内节点数；N为形函数；θ为温度自变量。

将（5）式代入（4）式中，并且考虑到δφ的任意性，可以得到离散后的瞬态热传导有限元求解方程为

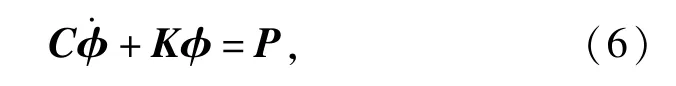
式中:C为热容矩阵；K为热传导矩阵；P是温度载荷向量；φ为节点温度向量是节点温度向量对时间的导数。C、K以及P中的元素由单元的相应的矩阵元素集成为

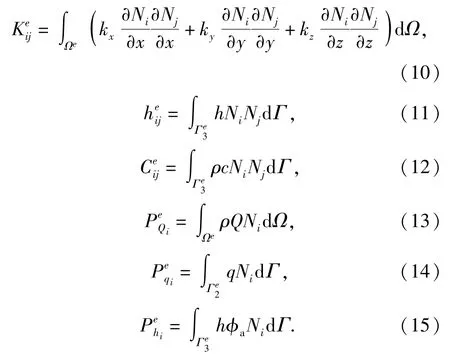
通过上述公式，已经将时间域和空间域的偏微分方程在空间域内离散为用节点温度表示的常微分方程。

2　自动机结构热故障分析

自动机设计时考虑气体密封性等原因，各零件间间隙量都进行了严格控制，以保证各项战斗指标满足规定要求。部分结构简图如图1所示。

连续高速射击后，自动机各部分零件温度都有不同程度的升高。基体、后衬套、前衬套与箱体的热膨胀对自动机机构运动的影响［6］，引起自动机工作故障。

2.1后衬套热膨胀分析

由于后衬套结构相对简单，可应用理论计算方法得到其热膨胀量。为对比有限元热分析方法和理论计算结果的一致性，分别运用有限元方法和理论计算来分析后衬套的热膨胀轴向伸长量［7-8］。

假定后衬套与前衬套端面的最大实测间隙量为Δmax，当后衬套温度为θbu时，前衬套与后衬套之间的热变形过盈量为

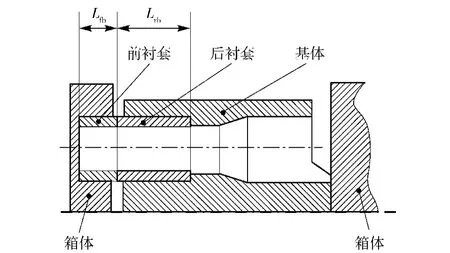
图1　结构简图Fig.1 Structural diagram

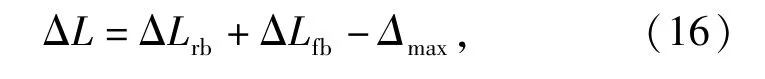
式中:ΔLrb为后衬套在θbu时的伸长量；ΔLfb为前衬套的有效热伸长量。

运动开始位置，机构作用力在基体上形成前推动力扭矩Tbtf:

式中:F为外力；β为作用力压力角；dbtf为力作用法线到机构运动轴线间的距离。

阻力扭矩包括热变形过盈量作用于基体上形成阻力扭矩Tbrf和由于基体与箱体热膨胀产生的阻力矩（作用在基体上）Tbcrf，其表达式分别为

式中:f为前衬套与后衬套间的静摩擦系数；Ab为基体配合端截面积；db为衬套轴线到机构旋转轴线间的距离；d为配合面到机构旋转轴线间的距离；L= Lfb+Lrb；Fbu为后衬套上产生的变形力为

Arb为后衬套截面积，E为弹性模量。

当后衬套温度为tbu时，热变形过盈量作用于基体形成阻力扭矩（Tbrf+Tbcrf）大于外力作用在基体上形成运动扭矩Tbtf时，则基体被锁死，机构不能完成预定的动作。

为此，要使基体不被锁死，则阻力扭矩Tbrf必须不大于复进扭矩Tbtf，计算可得临界热变形过盈量为

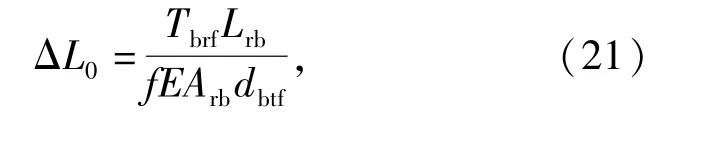
因此，在设计过程中只要热变形过盈量不大于ΔL0，就能够保证各机构的正常工作。

2.2临界温度计算

假定后衬套与前衬套间的初始间隙为ΔLini，则消除此间隙量的温度为

式中:α为材料的热膨胀系数。在消除该间隙量的温度下，到达临界热变形过盈量ΔL0所需温度增量为

因此满足机构正常工作的临界温度为

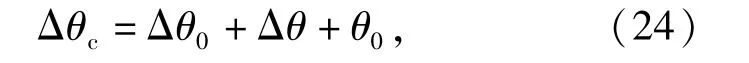
式中:θ0为室温。

由此可知:如果后衬套的实际温度小于临界温度Δθc时，能保证各机构的正常运行。出现故障时，衬套实测温度为θbu，其高于由（24）式所计算的临界温度值Δθc；自动机构停止工作后，随着温度在自然状态下不断下降，机构恢复工作。至此，自动机停射故障发生的根本原因得以明确:从热膨胀伸长量这一方面来说，当温度下降到正常工作温度后，自动机重新开始工作；从理论计算角度来说，故障得以复现。

2.3结构设计

前述计算时温度为θcf，如果温度升高到θmax（试验测试的最高炮口温度），按各零件的温度分布关系估算后衬套、前衬套的计算温度为θrbc和θfbc及相应的热膨胀量为Δrbc和Δfbc，见表1.

表1　温度θmax零件估算温度及热膨胀量Tab.1 Calculated temperature and thermal expansion amount atθmax

由此可算得热膨胀后零件间的变形增加量La为

为了保证温度在θmax下机构也能够正常工作，须满足尺寸关系:

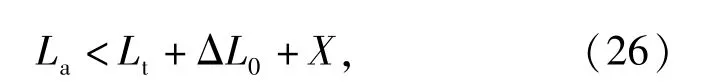
式中:Lt为前衬套及后衬套理论间隙；X为后衬套磨削量。

由（26）式得

为了保证自动机正常工作，X的取值须大于0.457mm（圆整为0.5 mm），也就是说须将后衬套磨短0.5mm.

3　算例

3.1自动机温度场仿真

射击停止后，用红外测温仪测量各零件不同位置的温度，计算用材料性能参数及温度见表2.

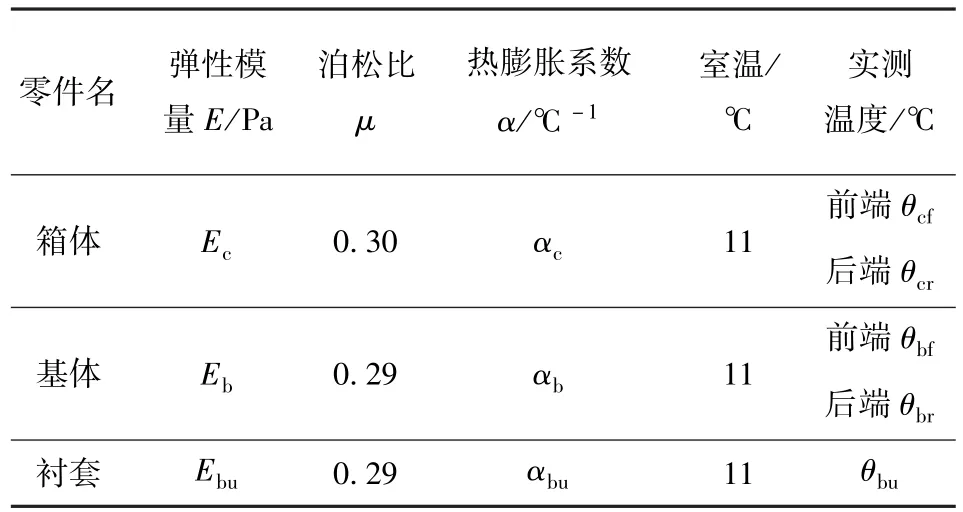
表2　计算用材料性能参数及温度Tab.2 Performance parameters and temperatures of materials used for calculation

图2　后衬套热膨胀分析Fig.2 Thermal analysis of rear bushing

图3　前衬套热膨胀分析Fig.3 Thermal analysis of front bushing

利用有限元软件（ABAQUS）及表2所列的材料参数和温度条件分别对前后衬套、基体和箱体进行有限元分析，计算结果如图2～图5所示（图中所示为位移量，单位mm），对应的计算结果如表3所示。

图4　基体热膨胀分析Fig.4 Thermal analysis of basic body

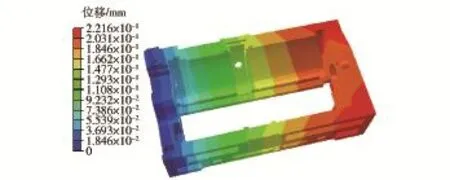
图5　箱体热膨胀分析Fig.5 Thermal analysis of box

表3　热膨胀量Tab.3 Thermal expansion amount

3.2试验

为了充分验证结构改进是否能满足各项性能指标要求，分别进行了常规试验和最高温度极限试验。

3.2.1常规试验

装弹100发，按每组15发间隔6 s连续进行多组实弹射击试验，当炮口温度达到220℃时停止射击，试验状态数据如表4所示。

表4　15发连续5组射击试验结果Tab.4 Firing rate and muzzle temperature in the firing of15 projectiles in each group

上述试验在寒区进行，室外温度-1.6℃.从试验结果可以看出，射速满足设计要求（由于此高射速自动机采用内能源形式，射速是其最重要的一项性能指标。然而由于结构尺寸缩短，结构间间隙量增加，设计改进是否影响射速必须予以重点关注）。试验结果表明，当炮口温度达到甚至超过220℃时，该自动机仍能正常工作。

3.2.2最高温度极限试验

按常规射击方式，进行多轮多组实弹试验，试验状态数据如表5所示。

表5　3轮5组试验射击结果Tab.5 Firing rate and muzzle temperature in 3 rounds of test

从试验结果可以看出（寒区，室外温度-5.6℃），修改了前后衬套的配合间隙量后，射速满足设计要求，当炮口温度达到384℃时（超过结构修前的临界温度220℃），该自动机仍能正常工作。

4　结论

由自动机工作原理和相关力学计算可知，当温度为θbu时，因热变形而作用于基体上的扭矩大于外力（来自于复进机构的弹簧力）作用于基体上的扭矩，故在此温度时，机构锁死，出现停射故障。

当后衬套上的临界温度为220℃，临界热变形过盈量为ΔL，此时要使机构能稳定地正常工作，必须将后衬套尺寸减小0.5 mm.在不同的试验条件下，该自动机都能满足性能指标的要求，设计改进达到预期目标，进而有效地验证了本文所采用的热-结构耦合仿真分析方法的适用性，因而此方法对于结构设计及其改进有现实的指导意义。

（References）

［1］ 张剑.气压盘式制动器热-结构耦合与热衰退性能研究［D］.镇江:江苏大学，2013. ZHANG Jian.Research of the thermal-structure coupling and the heat-fade performance on air disc brakes［D］.Zhenjiang:Jiangsu University，2013.（in Chinese）

［2］ 李金良，肖楠，谢基龙.重载货车车轮踏面制动辐板热应力分析［J］.机械工程学报，2012，48（12）:133-138. LI Jin-liang，XIAO Nan，XIE Ji-long.Thermal stress analysis of the heavy-haul freight cars wheel web plate under the wheel tread braking［J］.Journal of Mechanical Engineering，2012，48（12）: 133-138.（in Chinese）

［3］ 王丽.星载抛物面天线在轨热-结构耦合分析［D］.哈尔滨:哈尔滨工业大学，2011. WANG Li.Research on thermal-structural analysis of in-orbit parabolidal satellite antenna［D］.Harbin:Harbin Institute of Technology，2011.（in Chinese）

［4］ 李代金，罗凯，党建军，等.超空泡水下航行器空间运动建模与弹道仿真［J］.兵工学报，2012，33（8）:956-961. LI Dai-jin，LUO Kai，DANG Jian-jun，et al.Kinematic modeling and trajectory simulation for underwater supercavitating vehicles［J］.Acta Armamentarii，2012，33（8）:956-961.（in Chinese）

［5］ 苏晓鹏，钱林方，戴劲松，等.高射速自动机身管热容量及热应力分析［J］.南京理工大学学报，2009，33（4）:112-117. SU Xiao-peng，QIAN Lin-fang，DAI Jin-song，et al.Thermal capacity and thermal stress analysis of rapid-fire gun barrel［J］. Journal of Nanjing University of Science and Technology，2009，33（4）:112-117.（in Chinese）

［6］ 严宗达，王洪礼.热应力［M］.北京:高等教育出版社，1993. YAN Zong-da，WANG Hong-li.Thermal stress［M］.Beijing: Higher Education Press，1993.（in Chinese）

［7］ 吴永海，徐诚，陆昌龙，等.某速射火炮身管系统传热特性的数值仿真研究［J］.系统仿真学报，2007，19（19）:4407-4410. WU Yong-hai，XU Cheng，LU Chang-long，et al.Numerical study of heat-transfer characteristics of rapid-fire gun barrel system［J］.Journal of System Simulation，2007，19（19）:4407-4410.（in Chinese）

［8］ 胡振杰.火炮发射过程中的身管热弹耦合分析［D］.南京:南京理工大学，2007. HU Zhen-jie.Gun launch process in tube heat-elasticity coupling analysis［D］.Nanjing:Nanjing University of Science and Technology，2007.（in Chinese）

Analysis about Thermal-structure Coupling Effect of High Firing Rate Automatic Mechanism of a Gun

DAI Yong1，2，QIAN Lin-fang1，WU Xiao-jin2，XU Ya-dong1
（1.School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，Jiangsu，China；2.Product Research and Development Center，Chongqing Wangjiang Industry Co.，Ltd.，Chongqing 400071，China）

The prototype of a high firing rate automatic mechanism of a gun has a periodic fire stop failure during firing.The classical thermal expansion theory and the finite element method are used for the thermal-structure coupling analysis of high firing rate automatic mechanism.The analysis results show that the size of its structure can be appropriately adjusted to meet the requirement of the current firing rate and further improve the rate of fire.The improved structural design of demonstration prototype has non periodic fire stop phenomenon after several rounds of live ammunition tests.Thermal-structure coupling method can be used to solve similar failures in engineering practice.

ordnance science and technology；automatic mechanism；finite element；thermal-structure coupling

TJ303+.3

A

1000-1093（2016）09-1738-06

10.3969/j.issn.1000-1093.2016.09.026

2016-01-07

中国兵器装备集团公司“十二五”预先研究项目（JP606）

戴涌（1968—），男，研究员级高级工程师，博士研究生。E-mail:daiyong@cqwj.com；钱林方（1961—），男，教授，博士生导师。E-mail:lfqian@vip.163.com