选择性集成极限学习机分类器建模研究

徐晓杨　纪志成

(江南大学物联网工程学院　江苏 无锡 214122)



选择性集成极限学习机分类器建模研究

徐晓杨纪志成

(江南大学物联网工程学院江苏 无锡 214122)

极限学习机ELM(Extreme Learning Machine)具有训练过程极为快速的优点,但在实际分类应用中ELM分类器的分类精度和稳定性有时并不能满足要求。针对这一问题，在ELM用于分类时引入一种训练结果信息量评价指标来改进输出权值矩阵的求解方法，并增加隐层输出矩阵竞争机制来提高ELM的稳定性。为了进一步提高ELM的分类正确率，借鉴神经网络集成的理论，提出一种选择性集成ELM分类器。在集成方法中采用改进Bagging法并提出一种基于网络参数向量的相似度评价方法和选择性集成策略。最后通过UCI数据测试表明，同Bagging法和传统的全集成法相比，该方法拥有更为优秀的分类性能。

极限学习机神经网络选择性集成Bagging

0　引　言

极限学习机ELM是由Huang等[1,2]提出的一种基于单隐层前馈神经网络模型(SLFNs)的新型学习算法。它区别于传统神经网络的最大特点在于整个训练过程只需要一步，无需反复对网络中的众多参数进行复杂的迭代运算。所以，极限学习机的训练过程极为快速，同时具备良好的泛化性能。但是ELM同样也存在诸多不足，ELM的输入权值、隐层偏置均为随机产生，这些参数的随机性也使得最终生成的ELM模型的性能不具稳定性。另外，ELM中转移函数和隐层神经元数量的选择至今也没有一个广泛适用的理论体系的指导。如果缺乏应用背景的先验知识，那么往往需要耗费大量的精力才能最终获得一个性能良好的ELM模型。

Hansen等[3]于1990年首创性地提出了关于神经网络集成的方法与理论。他们通过实验证明如果先训练多个神经网络再进行组合就可以把整个神经网络系统的泛化能力显著的提高。Sollich等于1996给出了神经网络集成的定义[3]：将有限个神经网络对同一问题进行学习，最终整个系统在某个输入下的输出由构建此系统的神经网络共同决定。Krogh等则给出了神经网络集成的泛化误差公式[3]，该公式明确指出如果构成系统的子网络泛化能力越强同时子网络之间的相似度越低，那么系统的泛化误差就越小。在此之后，Zhou等[4]通过使用遗传算法，在所有的子网络中选择出部分进行集成，并证明了相较于集成所有子网络的系统，选择性集成了泛化能力强并且相似度低的子网络的系统往往能够拥有更好的泛化性能。

综上所述，为了进一步提高ELM模型的分类性能同时改善ELM的缺陷与不足，本文利用神经网络集成的方法与理论对ELM进行选择性集成。在ELM的选择性集成过程中，如何产生泛化能力强并且相似度低的子ELM模型，如何评价子网络之间的相似度以及采用何种策略去选择子网络集成是选择性ELM集成方法研究的关键问题。本文针对上述问题，在子ELM模型的生成过程中，引入一种训练结果信息量评价指标来改进输出权值矩阵的求解方法，并在隐层输出矩阵随机生成时增加隐层输出矩阵竞争机制，以此来加强子网络的性能和稳定性。在ELM集成时，采用改进的Bagging算法来降低子网络之间的相似度，并提出一种基于网络参数向量的相似度评价方法对子ELM模型进行选择性集成。最后，通过UCI中的数据对本文提出的选择性集成ELM分类器的效果进行测试与分析。

1　极限学习机(ELM)及其优化

1.1ELM的基本思想

对于任意给出的N个不同的训练样本(xi,ti)，其中xi=[xi1,xi2,…,xin]T∈Rn是该样本的n维输入数据，ti=[ti1,ti2,…,tim]T∈Rm是该样本的m维期望输出，选定一个在任意区间上无线可微的函数作为网络的转移函数g(·)，并设置网络的隐层神经元个数为L，则该SLFNs模型的输出可表示为：

(1)

式中wi=[wi1,wi2,…,win]T是第i个隐层节点与n维输入数据的输入权值，θi是第i个隐层节点的偏置，βi=[βi1,βi2,…,βim]T是第i个隐层节点与m维输出的输出权值，yi=[yi1,yi2,…,yim]T是第i个输入数据通过SLFNs模型得出的实际输出，式(1)可以简写为：

Hβ=Y

(2)

其中：

式中，H矩阵被称为隐层输出矩阵，因为wi、θi的值都是随机确定的，所以在给定输入数据后矩阵H就是一个已知的确定矩阵。因此极限学习机的核心问题就是求取最优的输出权值矩阵来使网络拥有最佳的性能。Bartlett在文献[5]中指出，当多个SLFNs具有基本相当的拟合性能时，输出权值范数较小的网络其泛化性能将会更加优秀。统计学理论的研究也同样发现：实验风险可以分为经验风险与结构风险两种。一种具备良好性能的神经网络应该充分考虑这两种风险，并在它们之间找到一个合适的平衡点[6]。所以，可以将输出权值矩阵β的求解问题转换为求解下面的最优问题：

(3)

其中‖ε‖2代表ELM模型中的经验风险，α则为经验风险的惩罚系数，相应的‖β‖2就代表了模型中的结构风险。通过拉格朗日方程将其转换为一个无条件的极值问题，可以求得：

β=(α-1I+HTH)†HTT

(4)

其中I代表单位矩阵,A†代表A的Moore-Penrose广义逆。如果A为非奇异矩阵，则A†可以表示为(ATA)-1AT。利用式(4)，ELM模型对于输入x的输出f(x)即可表示为：

(5)

由于本文仅讨论ELM模型用于分类时的情形，所以最终的分类结果y可以表示为：

y={j|fj(x)=max{fi(x),i=1,2,…,m}}

(6)

1.2加入信息量评价的ELM分类模型

神经网络作为分类器使用时，实际上是一种基于概率的分类器。如果式(6)中fi(x)对应的数值越大，则说明输入x属于类别i的概率就越大；同样的如果fi(x)对应的数值越小，就说明x属于类别i的概率越小。通过下式可以很容易将ELM的分类结果以概率的形式输出：

(7)

(8)

式中，Pi(x)表示输入x属于类别i的概率。当Pi(x)的概率越大而其他的概率越小时，表明在特征空间中该样本和决策超平面的距离越远，分类器对该数据的分类结果越有把握；反之，分类器对分类结果就越不确定[7]。为了更加直观地阐明本文对ELM分类器的优化原理，先来看一组例子。假设有一组三分类的训练样本(x,t)且t=0(x对应的类别编号为0)，那么在ELM模型中t=[1,-1,-1]。如果有两个ELM模型A和B对它的训练结果分别为yA=[1.5,-0.5,-0.5]和yB=[0.5，-0.5,-0.5]，那么有‖εA‖2=‖εB‖2，如果又有‖βA‖2≈‖βB‖2。根据式(3)模型A和B应该拥有十分相近的分类性能，但根据文献[7]中的论述，模型A的性能要优于模型B的性能。本文受此启发，基于文献[7]中的理论对式(3)进行改写。在特征空间中样本和决策超平面的距离可以由输出矩阵Y中各个元素的方差表示，方差越大则说明距离越远,分类效果越好。在矩阵中，矩阵的最大特征值λmax可以用来评价矩阵在特征空间中的方差，这在一些数据分析法中也被称为信息量。根据定义又有‖Y‖2=λmax，因此‖Y‖2可以用来评价ELM模型输出矩阵中信息量的大小，在相近条件下，输出矩阵中信息量大的模型将会具备更加优秀的分类性能。所以式(3)可以按如下改写：

(9)

其中，γ为输出矩阵信息量的奖励系数。同样的，再次运用拉格朗日方程将上式变换为一个无条件的极值问题,其中δ=[δ1,δ2,…,δN]T,δi∈Rm、μ=[μ1,μ2,…,μN]T,μi∈Rm均为相应的拉格朗日乘子。

δ(Hβ-T-ε)-μ(Hβ-Y)

(10)

对式(10)中的各变量求偏导并令其结果为0即可得到式(11):

(11)

再根据式(11)可得：

β=[α-1I+(I-α-1γ)HTH]†HTT

(12)

那么式(5)也就应该改写为：

f(x)=h(x)[α-1I+(1-α-1γ)HTH]†HTT

(13)

由式(12)求出的输出权值矩阵β充分考虑了ELM在用作分类器时的拟合性、泛化性和训练输出结果所带的信息量，且不难看出当γ=0时式(12)就退化成了式(4)。

1.3隐层输出矩阵竞争机制

上文中通过加入信息量评价指标对的求解进行优化，但隐层输出矩阵H的生成仍然是随机的，这些随机参数的合适与否将直接影响ELM模型的性能。许多学者也意识到了这个问题，Zhu等[8]提出把‖ε‖2作为适应度函数并运用进化算法对H矩阵进行寻优，但单纯提高ELM的训练精度并不代表ELM的性能就会得到提升；陈涵瀛等[9]将H矩阵的求解问题转化为了多目标优化问题，将‖ε‖2和‖β‖2作为两个独立的目标函数对H矩阵进行双目标寻优，但是其忽略了‖ε‖2和‖β‖2之间大致的权重关系，并且在求得的Pareto最优解集中选择出合适的解也是较为困难的。更为严重的是这些学者都忽略了关键的一点：ELM中随机参数的总数=(m+1)×L，其中m为输入数据的维数，L为隐层节点的数量。当m和L较大时随机参数的数量就会变得很大，如果直接对这些参数进行寻优就会引发维数灾难。运用群智能算法在高维解空间中寻优时不得不大幅增加种群规模和迭代次数，求解H矩阵就会消耗大量的时间，ELM模型训练极为快速的优势也就被大大削弱了。本文为解决这一问题提出了隐层输出矩阵竞争机制，先随机产生有限组参数集并形成对应的Hi矩阵，再通过加权组合形成最终的H矩阵：

(14)

其中ηi称之为竞争系数，倘若Hi的竞争力越强那么ηi的数值就会越大。数组η=[η1,η2,…,ηk]取值的不同就会产生无限多个H矩阵，本文把对随机参数本身的寻优策略改为对数组η=[η1,η2,…,ηk]的寻优，这样就能够显著地降低解空间的维数，大幅缩短寻优的时间。把式(9)作为适应度函数同时选用式(12)作为β的求解公式，然后运用粒子群算法寻找出最优的数组η并组合出对应的H矩阵。ELM分类器的具体构造步骤如下所示，其中粒子群算法的具体内容请详见文献[10]本文中就不再赘述。

(a) 确定参与竞争的隐层输出矩阵个数P,并随机生成P个隐层输出矩阵Hi，i=1,2,…,P。

(d) 确定粒子群算法的迭代次数C，再通过式(14)求得与ηi对应的H矩阵并将式(9)作为适应度函数开始进行寻优直至C次迭代全部完成，在粒子群算法的每一次迭代过程中需要满足式(14)中的约束条件。

(e) 将迭代求得的最优数组ηoptimal根据式(14)确定对应的最优H矩阵，再通过式(12)求出β矩阵，确定H和β后就可以根据式(13)构造出优化ELM分类器，至此ELM分类器的构造就完成了。

理论上，P、S以及C设置的越大H矩阵的优化效果越好，但是为了控制寻优时间需要根据实际情况设置合适的值。

2　选择性集成

选择性ELM集成的第一步就是要生成一定数量且之间具有一定差异度的子ELM模型。可以设想一下如果每一个子ELM模型都十分相似，那么它们对相同输入的输出也会十分相似。把这些相似的子网络集成在一起只会白白增加建模的复杂度而对网络性能的提升起不到明显的作用。为解决这一问题，本文采用Bagging法并加以改进来降低子网络之间的相似度。根据文献[6]的论述，选择性集成泛化能力强并且相似度低的子网络的系统往往能够拥有比集成所有子网络的系统更好的泛化性能，那么一种有效的相似度评价方法将会对系统的选择性集成起到正确的指导作用。本文提出一种基于子网络参数向量的相似度评价方法和选择性集成策略，并通过其构建最终的选择性集成ELM分类器模型。本文所述选择性ELM集成方法的基本流程如图1所示。

图1　本文选择性ELM集成方法的基本流程

2.1基于改进Bagging算法的个体网络生成

Bagging算法是一种多学习算法的集成技术，它的核心基础是可重复随机取样[3]。每一个子网络的训练样本集都从原始训练样本集中随机抽取，且通常来说新生成的训练样本集规模和原始训练样本集规模相当。由于采取有放回的抽取方式所以原始训练样本集中的某一样本可能被抽取多次也可能一次未被抽取。这样就在各个子网络的训练样本集上构造出了差异性，且新生成的训练样本集平均约含有63.2%的原始训练样本集内容。

但Bagging法的取样方式具有比较大的盲目性，随机取样并不能有效遍历整个原始样本集，也就无法充分反映出原始样本集中样本的空间分布情况，这对训练出的子网络性能有很大的影响。本文将分层抽样的思想引入Bagging法中，先按照各个样本所对应的类别将原始样本集分层，再在每一层样本集中使用Bagging法采样。完成后将各层的采样集进行组合即可得到一个新的训练样本集，这样的采样方法既能够构造出差异性又能够保证新训练集的采样质量。为了进一步增大子网络之间的差异性，在“Sigmoid”、“Sine”和“Hardlim”函数之中随机选取一个作为子网络的转移函数g(·)。

2.2子网络的相似度评价

在许多关于神经网络集成的文献中都给出了其相似度评价的方法。陆慧娟等[11]根据子网络对测试样本集的输出结果来评价子网络的相似度，输出结果越不一致则相似度越低，但不同的测试样本集就会得出不同的相似度结果，结果可能具有偶然性；Rahman等[12]则运用聚类技术对子网络进行相似度评价，但聚类数目难以确定且过程略有繁琐。

本文提出一种基于子网络参数向量的相似度评价方法。由ELM的基本原理可知：y=h(x)β，所以给定输入的输出是根据H矩阵和β矩阵来求解的。在子网络结构确定的前提下子网络的差异性主要体现在构成H矩阵和β矩阵的参数集上。通过子网络的参数集而不是输出结果可以更为本质地评价子网络的相似度而不会受到测试样本集的影响。

对于一个输入有n种属性而输出有m种类别的分类问题而言，如果网络i有L个隐层神经元那么网络i中就有n×L个输入权值、L个隐层偏置和m×L个输出权值共记(m+n+1)×L个参数，将这些参数组成一个向量ci=(ω1,…,β1,…,θL)。根据定义，向量a和b的内积可表示为：

〈a,b〉=‖a‖·‖b‖cosθ

(15)

由式(15)可知cosθ的大小可以作为一种评价向量a和b相似程度的定量指标。基于余弦定理的向量相似度评价公式有许多种变形，张宇等[13]给出了较为详细的阐述，本文选用Dice系数法作为评价向量相似度的方法，其计算公式如下：

(16)

易知Sim(ci,cj)的值域为[-1,1],当Sim(ci,cj)越小时相似度越低同时也说明子网络i和j的相似度越低。特别当ci=cj时有Sim(ci,cj)=1，而当ci=-cj时有Sim(ci,cj)=-1。根据式(16)就可以对任意两个子网络的相似度做出定量的评价。

2.3选择性集成策略

通过式(16)把Q个子网络两两之间的相似度求出，用Simij来表示子网络i和j的相似度，那么可以得到这Q个子网络的相似度矩阵Similarity：

(17)

显然，Similarity是一个对称矩阵并且对角线元素都为1。为了方便下文中对相似度阈值ψ的设置，需要对Similarity中的元素大小进行归一化处理。本文使用Matlab中mapminmax()函数将矩阵中除对角线上的所有元素归一化到[0,1]之间。

根据Krogh等[3]给出的神经网络集成泛化误差公式：

(18)

(a) 通过改进Bagging法和本文第一节中所述的方法生成有限个ELM子网络。

(b) 选用原始训练样本集对每一个子网络进行测试并按照式(9)求出每一个子网络的泛化误差，完成后按泛化误差从小到大的顺序对子网络进行排序。

(c) 根据实际情况设置一个泛化误差阈值φ并把泛化误差大于φ的子网络全部剔除，一般来说剔除总数的20%～30%较为合适，剩下的Q个子网络即可组成精英子网络集net=[net1, net2,…, netQ]。

(d) 求出net中所有子网络两两之间的相似度并得出相似度矩阵Similarity。再设置一个相似度阈值ψ，从第一行中的元素开始比对如果Simij>ψ&&i≠j就把netj从net中剔除同时将矩阵Similarity的第j行也删除掉，如此操作直至Similarity的所有行都比对完成。此时，net中剩余的Q′个子网络即是选择出用于集成的泛化能力强且相似度低的优秀个体。

(e) 对每一个子网络neti设置一个权值ρi，ρi按如下方法设置：首先将步骤(b)中求得的各子网络的泛化误差通过下式归一化到[0,1]之间：

(19)

(20)

最后构造出最终的选择性集成ELM分类器模型，且模型的输出可表示为f(x)=ρ1f1(x)+ρ2f2(x)+…+ρQ′fQ′(x),最终的分类结果则可根据式(6)得出。

3　实验与分析

上文中论述了选择性集成ELM分类器ELMSE(Extreme Learning Machine Selective Ensemble)的方法与理论。在本节中为了测试ELMSE方法的有效性，将在UCI数据库中选择5组分类数据集进行仿真测试。为了更加直观和形象地说明ELMSE的分类性能，在仿真测试中还将加入经典ELM模型、本文第1节中提出的改进ELM模型(IELM)、Bagging法集成模型和全集成ELM模型(ALL-EE)作为参照对象。其中Bagging法的具体内容参照文献[14]，只不过将文献[14]中的PNN网络改为ELM。ALL-EE方法与ELMSE基本类似，只是最后对生成的子网络全部集成，没有选择性集成的步骤。

在UCI中分别选取Glass、Iris、Heart、Letter和Wine这五个数据集作为本次实验的数据，它们的基本信息如表1所示。

表1　实验所用数据集基本信息

为了避免实验中可能出现的偶然性并进一步增强实验的说服力，本文采取5次交叉验证。先将各个数据集平均分成5份并且尽量保证每一份中各个类别的样本所占的比例基本相同；然后依次选取每一份作为测试集剩下的4份则自动变为训练集，将5次测试得出的分类准确率平均后作为最终结果。在使用这些数据集前，先对它们进行归一化处理来消除样本中各个属性不同量纲对网络训练效果的影响。在参数选择方面式(9)中的α取1，γ取0.2，1.3节中P、S、C这三个参数在试验中统一设置为6、20和50。选择性集成中的泛化误差阈值φ可以根据子网络的整体情况调整而相似度阈值ψ取0.7，隐层神经元的个数L和子网络的生成个数可以根据数据集中样本的属性数和类别数进行适当调整。以数据集Wine为例，φ取20，L取10，子网络生成个数取40。本次实验的结果如表2-表4所示，其中表2为单一ELM分类器的对比而表3、表4则为三种不同集成方式之间的对比。

表2　单一ELM模型分类正确率

表3　三种不同集成网络的分类正确率

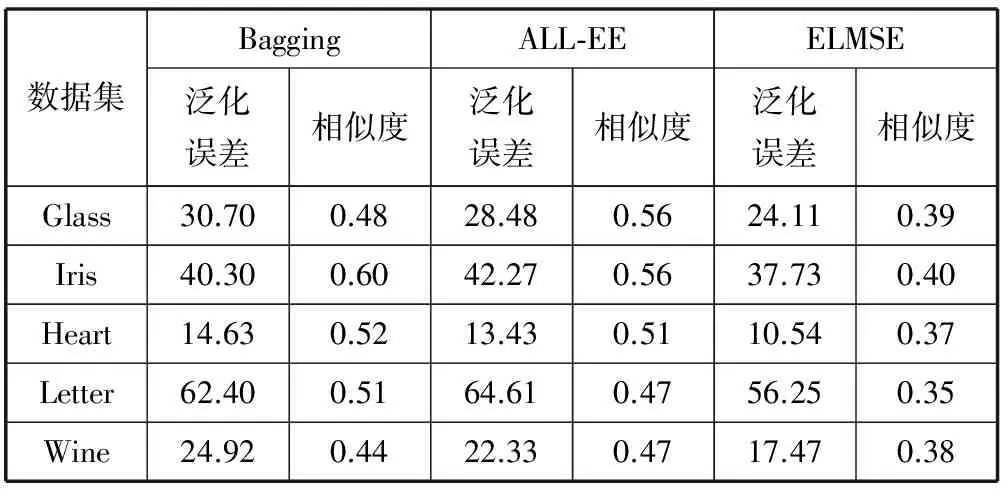
表4　网络关键指标对比

由表2可知，IELM在4个数据集中的分类精度都要优于原始ELM模型，且在Glass和Letter数据集上的优势更为明显。这是因为Glass和Letter都属于多属性多分类的复杂问题，原始ELM比较容易得出不确定的分类结果从而降低分类的正确率，而IELM则通过上文中的改进一定程度上地避免了这种问题。

从表3和表4中3种不同集成方法的比较可以看出，ELMSE在系统平均泛化误差和平均相似度这两项关键指标上都比其他方法更为优异并且总体上分类正确率也更高。这一实验结果验证了Zhou等[6]的结论同时也说明本文第2节提出的相似度评价方法和选择性集成策略是有效的，和其他几种方法相比能够使集成的ELM网络拥有更佳的分类性能。

4　结　语

本文针对ELM分类器在实际应用中性能不稳定、精度不高的问题，通过深入研究ELM分类器的模型提出了一种评价训练结果中信息量大小的矩阵求解方法。并针对ELM模型中参数随机产出的不足，引入隐层输出矩阵竞争机制。在选择性集成方面，针对已有的子网络相似度评价方法的不足，提出了一种基于子网络参数向量的相似度评价方法和选择性集成策略并给出了具体的计算公式和集成步骤。通过UCI数据测试表明，本文提出的选择性集成ELM分类器能够比其他ELM分类器拥有更好的分类性能，为现实中复杂的分类问题提供了一种新的可行方案。

[1] Huang G B,Zhu Q Y,Siew C K.Extreme learning machine:theory and application[J].Neurocomputing,2006,70(1-3):489-501.

[2] Huang G B,Wang D H,Lan Y.Extreme learning machines:a survey[J].International Journal of Machine Learning and Cybernetics,2011,2(2):107-122.

[3] 周志华,陈世福.神经网络集成[J].计算机学报,2002,25(1):1-8.

[4] Zhou Z H,Wu J,Tang W.Ensembling neural networks:many could be better than all[J].Artificial intelligence,2002,137(1):239-263.

[5] Bartlett P L.The sample complexity of pattern classification with neural networks:the size of the weights is more important than the size of the network[J].IEEE Transactions on Information Theory,1998,44(2):525-536.

[6] Shipp C A,Kuncheva L I.Relationships between combination methods and measures of diversity in combining classifiers[J].Information Fusion,2002,3(2):135-148.

[7] Yang J,Yang J Y,Zhang D,et al.Feature fusion:parallel strategy vs.serial strategy[J].Pattern Recognition,2003,36(6):1369-1381.

[8] Zhu Q Y,Qin A K,Suganthan P N,et al.Evolutionary extreme learning machine[J].Pattern Recognition,2005,38(10):1759-1763.

[9] 陈涵瀛,高璞珍,谭思超,等.自然循环流动不稳定性的多目标优化极限学习机预测方法[J].物理学报,2014,63(20):111-118.

[10] 胥小波,郑康锋,李丹,等.新的混沌粒子群优化算法[J].通信学报,2012,33(1):24-30.

[11] 陆慧娟,安春霖,马小平,等.基于输出不一致测度的极限学习机集成的基因表达数据分类[J].计算机学报,2013,36(2):341-348.

[12] Rahman A,Verma B.Cluster-based ensemble of classifiers[J].Expert Systems,2013,30(3):270-282.

[13] 张宇,刘雨东,计钊.向量相似度测度方法[J].声学技术,2009,28(4):532-536.

[14] 蒋芸,陈娜,明利特,等.基于Bagging的概率神经网络集成分类算法[J].计算机科学,2013,40(5):242-246.

RESEARCH ON MODELLING SELECTIVE ENSEMBLE EXTREME LEARNING MACHINE CLASSIFIER

Xu XiaoyangJi Zhicheng

(School of Internet of Things Engineering,Jiangnan University,Wuxi 214122,Jiangsu,China)

As its advantage, the training speed of extreme learning machine (ELM) is extremely fast. But sometimes its stability and precision can’t meet the requirement of practical application. In order to solve the problem, this paper introduces a solution for ELM when to be used in classification, in it the output weight matrix is improved with the evaluation factor of information in training results. Meanwhile, the hidden layer output matrixes competitive mechanism is added to improve the stability of ELM. For the sake of further improving ELM’s accuracy rate in classification, we propose a kind of selective ensemble extreme learning machine classifier by learning from the theory of neural network ensemble. In ensemble method, we adopt the improved Bagging and propose a subnet’s parameter vector-based similarity evaluation method and selective ensemble policy. Finally it is demonstrated by UCI data test that compared with Bagging and traditional all ensemble ELM, the solution proposed here has better performance in classification.

Extreme learning machineNeural networkSelective ensembleBagging

2015-01-30。国家粮食局公益性科研项目(2013130 12)。徐晓杨，硕士生，主研领域：神经网络及其应用。纪志成，教授。

TP183

A

10.3969/j.issn.1000-386x.2016.09.065