一种执行机构工作空间边界提取方法
李元丰 张万欣
(中国航天员科研训练中心人因工程重点实验室 北京 100094)
一种执行机构工作空间边界提取方法
李元丰张万欣
(中国航天员科研训练中心人因工程重点实验室北京 100094)
工作空间边界的提取在机械臂等执行机构的设计及功能评价中是非常重要的处理操作。将执行机构工作空间点云转化为图像,结合灰度图像处理方法提出一种新型的执行机构工作空间边界提取方法。首先提出栅格密度算法,作为点云转化为灰度图像的转化算子,栅格密度描述了空间点云的分布情况,可用于分析机构灵巧度;然后采用数学形态学处理方法对灰度图像进行平滑处理和边缘检测;最后,利用坐标对应关系反算边界的坐标位置信息。以人体上肢可达域作为实验对象进行了算法验证,结果表明该算法可以快速、准确地提取人体上肢可达域的边界,且与其他算法相比在运算速度与精确度上具有优势。
执行机构工作空间边界提取栅格密度数学形态学
0 引 言
准确的计算工作空间对于机械臂等执行机构来说是确定其工作范围、评价工效性能的重要前提。正向算法是一种计算工作空间的有效算法,在执行机构每个自由度的活动范围内采样一定的步进,以数值试验的方式计算末端执行器的空间可达位置,从而构成空间点云表征的机构工作空间。相比于解析法,数值试验方法操作简单,可以规避解析法可能遇到的奇异解问题[1]。但由于正向算法获得的工作空间是由空间散乱点云表征的,包含了过多的信息,无法直观地读取有价值的特征信息,如工作空间的边界,因此对点云的后期处理就显得尤为重要。
工作空间的边界是工作空间的首要特征,通过对散乱点云进行处理,提取其曲面或者曲线边界包络是点云工作空间处理的重要研究内容。Rastegar[2]等人采用蒙特卡洛法计算工作空间边界;Ceccarelli[3]等人提出二值矩阵法;另外研究人员提出的边界提取算法还包括栅格法[4]、分段极值法[5]、局部点象限法[6]等。然而各算法都存在一定局限性,尤其是无法表征工作空间点云的分布密度情况,体现执行机构的灵巧度。机构的灵巧度是指执行机构从各个角度到达某一位置的难易程度。陈文斌[7]在研究中提出了点云的距离权重概念可部分解决该问题,然而该算法在计算速度、边界提取的精确度上存在一定的局限性。
本文提出一种新的执行机构工作空间边界提取方法。首先提出栅格密度概念,并以此作为算子将工作空间点云转化为灰度图像,从而将点云问题转化为图像处理问题。栅格密度可充分描述点云的空间分布情况,从获得的灰度图像中的灰度分布即可获得执行机构在空间内的灵巧度情况;利用数学形态学原理对灰度图像进行光滑处理和边缘检测,最终通过坐标对应关系获得执行机构工作空间边界。为验证算法的性能,对文献[8]中提出的人体上肢可达域进行了边界提取实验,实验结果证明了该方法的有效性。
1 方 法
1.1栅格密度算法

图1 栅格法原理示意图
传统栅格法提取边界的原理是将平面离散成一定大小的网格,根据各个栅格中是否包含数据点判断其是否位于工作区域内;再依据相邻栅格的拓扑结构关系判断此栅格是边界网格还是内部网格,据此确定边界点[1],如图1所示。
栅格密度算法是在栅格法将平面划分为一定数量的网格基础上引入了点密度概念,分别计算各网格中数据点的数量,从而获得各个网格中的点密度情况,组成密度矩阵。利用数据矩阵与灰度图像转化算法将密度矩阵转化为灰度图像,从而将点云问题转化为图像处理问题。
具体做法可表述为:选取一定栅格尺寸将平面划分为m×n个网格,分别计算各个网格中数据点的数量,对矩阵中元素进行归一化处理获得相对密度矩阵W:
(1)
密度矩阵中元素携带有数值和位置信息,表示的是相应位置栅格内数据点的相对密度。
进一步采用数据矩阵与灰度图像转化算法将密度矩阵W转化为灰度图像P:
(2)
灰度图像矩阵P中元素同样携带有数值和位置信息,表示的是相应位置像素点的灰度值。灰度值大小代表执行机构到达对应位置的难易程度,灰度值大表示容易到达,机构在此的灵巧度好,灰度值小表示不容易到达,机构在此的灵巧度低,灰度值为零则表示该位置不可到达。
密度矩阵W与灰度图像P为相互对应关系,即某栅格内相对密度wij唯一且与相应像素点上的灰度pij对应,而密度矩阵与灰度图像转化的过程实际就是建立起这样一种对应关系。
1.2数学形态学方法
1.2.1数学形态学基本理论
数学形态学是一种应用于图像处理的新方法,是在集合论的基础上发展而来的[9]。它以严格的数学理论和几何学为基础而又密切联系着实际,与其他的空域或频域图像处理和分析方法相比具有一系列明显的优势[10-12]。数学形态学方法处理图像的基本思想是利用结构元素作为“探针”,对目标图像进行“探测”,保留符合要求的信号而剔除其他信号[13,14]。数学形态学处理图像的核心内容是结构元素的选择,结构元素实际上是衡量图像信息的“标尺”,标尺标准的选定将直接影响图像处理的效果。
数学形态学定义了膨胀和腐蚀两种基本的运算。设A为目标图像,B为结构元素。
膨胀运算的定义为:
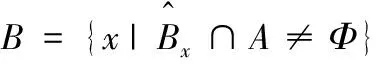
(3)
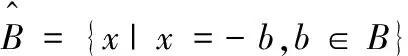
(4)
膨胀是一个扩张的过程,可以填充图像中的小孔及在图像边缘处的小凹陷部分。
腐蚀运算的定义为:
AΘB={x|Bx⊆A}
(5)
腐蚀是一个收缩的过程,可以消除图像中细小无意义的点。
通过膨胀和腐蚀的组合,获得开运算和闭运算两种扩展运算。采用相同的结构元素先进行腐蚀运算,后进行膨胀运算定义为开运算:
A∘B=(AΘB)⊕B
(6)
开运算可以平滑图像轮廓,去除图像中的细小点。
与开运算相反,采用相同的结构元素先进行膨胀运算,后进行腐蚀运算定义为闭运算:
A·B=(A⊕B)ΘB
(7)
闭运算可以填补图像的空洞和缺陷。
1.2.2灰度图像处理方法
利用数学形态学方法提取边界是借鉴于其在图像边缘检测中的应用。为排除灰度变化给边界提取带来的干扰,首先将灰度图像二值化。灰度图像二值化的关键在于分割阈值的确定,根据实际情况合理地选择阈值是准确提取图像信息的关键。常用的阈值确定方法有P片法、峰谷法[14]以及迭代法[15]等。
二值图难免会有缺陷或者噪声,因此选取结构元素B1,对图像进行开、闭运算滤波,平滑图像去除噪声。
依据数学形态学的基本运算,主要有以下几种典型的边缘检测算子[16]:
假设A为原图像,B2为结构元素,B(A)表示图像边缘。
(1) 腐蚀型
B(A)=A-AΘB2
(8)
(2) 膨胀型
B(A)=A⊕B2-A
(9)
(3) 膨胀腐蚀型
B(A)=(A⊕B2)-(AΘB2)
(10)
当然也可以通过基本运算的组合获得其他形式的形态学边缘检测算子。在本文中,以上基本检测算子已经可以满足要求。
1.3坐标对应关系
如前文所述,密度矩阵和灰度图像(包括二值化后的二值图像)中的元素均携带有位置以及数值信息,其中元素的位置信息是在栅格划分过程由平面坐标空间转化为矩阵中的位置参数。
假设平面点云的横纵坐标下限分别为xfloor和yfloor,栅格边长为Δlx和Δly,则灰度图像(或二值图)中的元素pij与平面坐标空间的坐标位置对应关系可描述为:
xp=xfloor+(j-1)·Δlx
(11)
yp=yfloor+(i-1)·Δly
(12)
式中,xp与yp表示图像元素对应于平面坐标空间的横纵坐标位置。
通过此对应关系可以实现图像像素位置与空间坐标位置参数的转化。因此,通过形态学处理运算提取后的灰度图像(二值图)的边界可以转化到坐标空间,反算点云边界的空间坐标位置。
2 实验及结果
为验证本文边界提取算法的有效性,采用文献[8]中所述的人体右手臂上肢可达域模型作为处理对象开展实验验证。人体坐标系定义如图2所示,X轴沿人体冠状轴方向,Y轴沿人体矢状轴方向,Z轴沿人体垂轴方向,坐标原点定义在左右肩关节中心连线中点[7]。
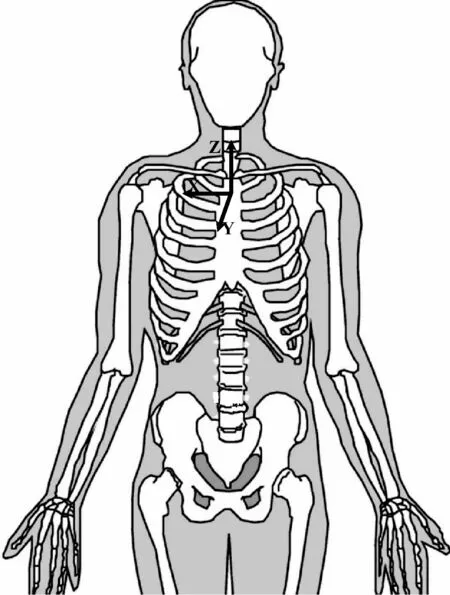
图2 人体坐标定义
人体上肢可达域模型包含6个关节旋转自由度,分别为内肩关节活动角度φrp和φde,外肩关节活动角度φA、φF、φR以及肘关节屈/伸运动角度φEF。依据表1中各个角度的活动范围,计算获得由4 278 655个点组成的人体上肢可达域空间点云。

表1 关节角度活动范围
算法过程及结果如下:
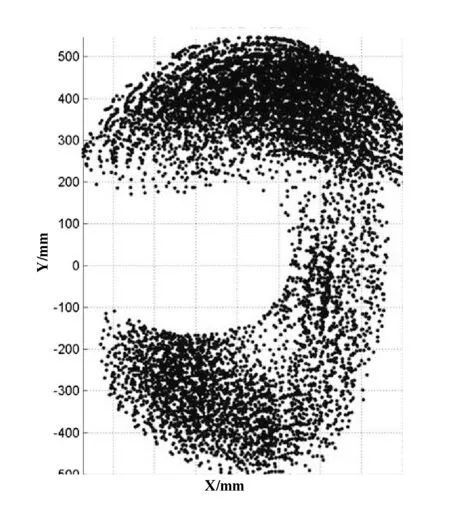
图3 平面点云分布
(1) 空间点云降维处理。以10 mm作为步长,将三维空间点云划分为103个平面点云组成。图3所示为选取的某一层点云分布。
(2) 计算栅格密度矩阵W。栅格设定为边长8 mm的正方形,计算每个栅格中的点分布密度情况,获得栅格密度矩阵W。
(3) 栅格密度矩阵转化为灰度图像。将密度矩阵归一化处理,设定矩阵中最大值元素为单位1,通过转化算法将密度矩阵转化为灰度图像,结果如图4(a)所示。灰度图像中的各处灰度并不相同,体现出人体上肢到达各个位置的难易程度的区别,即人体上肢的灵巧度,(b)为二值图边界。从图中可以看出,上肢在人体前部的灵巧度要好于在身体侧面和后面的灵巧度,该结论符合人体上肢的活动特性。

图4 数学形态学处理图像
(4) 灰度图像数学形态学平滑及边缘检测。首先根据灰度图像以及人体上肢可达域特点选取合适的阈值,将灰度图像二值化。
选取结构元素B1对二值图进行开、闭运算平滑处理,滤波去噪:
(13)
选取钻石形结构元素B2,通过腐蚀性边缘检测算子提取二值图像边界,提取结果如图4(b)所示。
(14)
(5) 利用坐标对应关系,计算获得边界空间坐标位置,图5(a)所示为提取的边界与点云图。实验结果表明,本文提出的提取算法可以有效地提取点云的边界,且精确度较好。
为了验证栅格密度算法的优越性,同时依据文献[7]提出的距离权重算法提取平面点云边界,进行对比验证,距离权重算法提取平面点云边界结果如图5(b)所示。首先定性比较两种方法的提取效果,两者边界均能描述边界特征。为了进一步定量对比点云边界精度,对比两种算法提取边界包络的上肢平面可达域的面积,如表2所示。由定性比较可知,两种算法提取的边界均实现对点云轮廓的包络,所以相比较而言,平面可达域面积较小的算法所提取的边界与点云的真实边界符合程度更高,点云与提取的边界间的空隙更少。因此可知,栅格密度算法更能准确地表述点云边界的特征,边界提取精度更好。另外,栅格密度算法在运算效率上也更具优势,在相同配置计算机上,两种算法的运行时间如表3所示,可见栅格密度算法的运算效率是距离权重算法效率的近14倍。
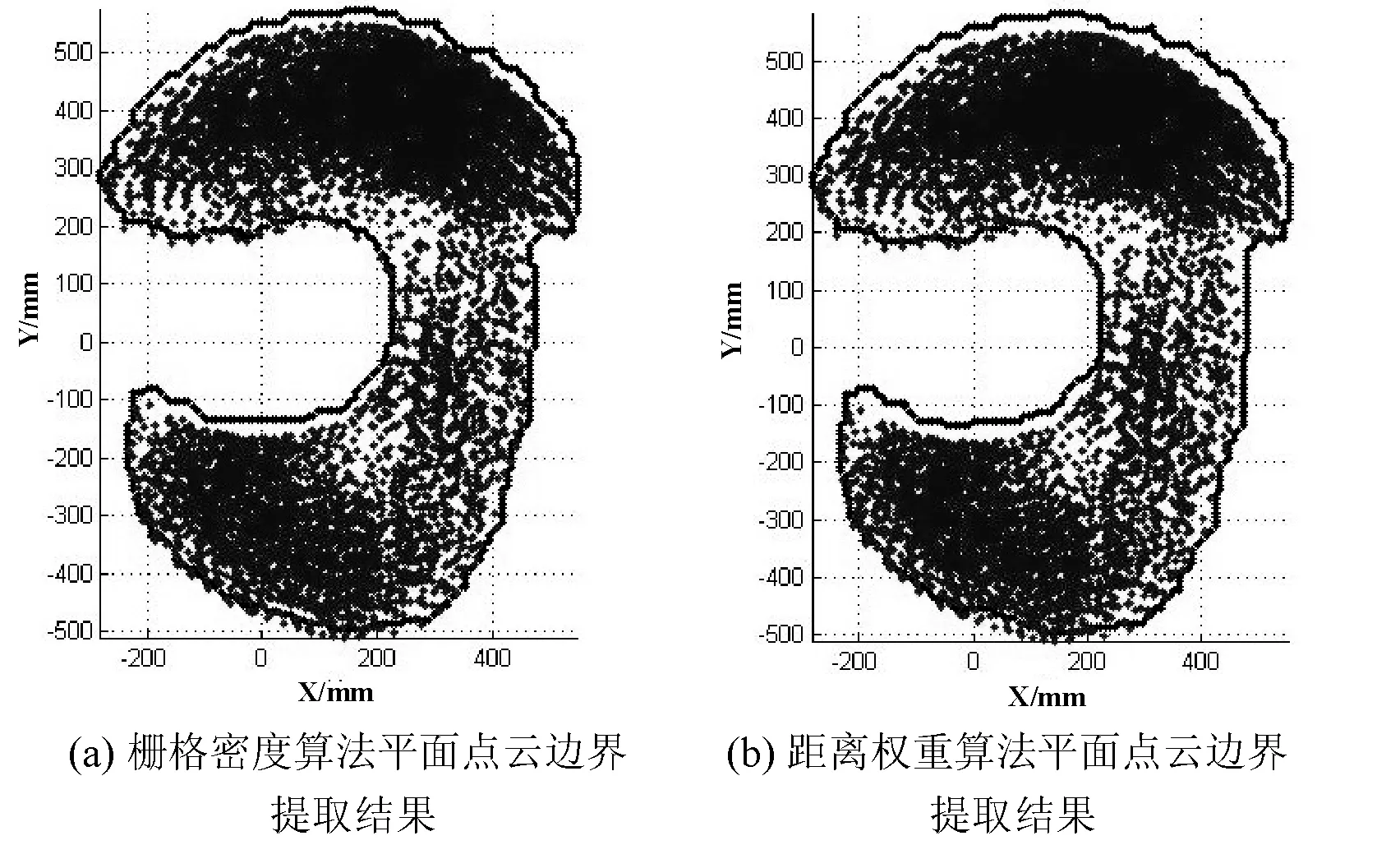
图5 平面点云边界提取结果
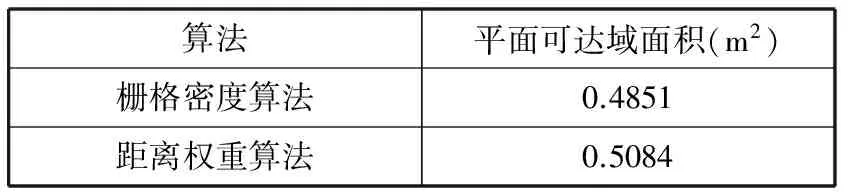
算法平面可达域面积(m2)栅格密度算法0.4851距离权重算法0.5084
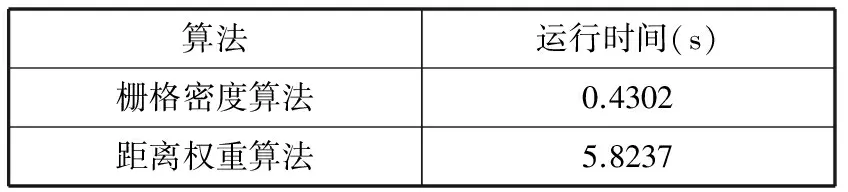
表3 算法运行时间对比
依次完成对各个高度等级的平面点云的边界提取,分别拟合连线,最终获得人体上肢可达域空间的包络边界,如图6所示。计算人体上肢可达域空间的体积为0.631 m3,结果与文献[7]中及文献[8]所述一致,证明本文提出的工作空间边界提取算法是有效的。

图6 上肢可达域边界提取结果
3 结 语
本文提出了一种针对执行机构的工作空间边界提取方法。创新地提出了栅格密度算法,将点云问题转化为灰度图像处理问题,结合数学形态学图像处理方法提取工作空间边界。所提出的栅格密度算法可应用于机构灵巧度分析。通过对人体上肢可达域模型工作空间点云边界的提取实验,验证了本文算法的有效性。同时通过对比实验,证明本文算法与其他算法相比在运算效率和提取精度等方面的优势。本文详细描述了算法的执行过程,可为相关的研究人员提供参照。
[1] 文剑.舱外航天服活动性能关键技术研究[D].北京交通大学,2011.
[2] Rastegar J,Perel D.Generation of manipulator workspace boundary geometry using the Monte Carlo method and interactive computer graphics[J].Journal of Mechanical Design,1990,112(3):452-454.
[3] Ceccarelli M,Angeles J.A numerical evaluation of the workspace of a seven-axis, redundant manipulator[C]//IEEE International Conference on Robotics and Automation,2000:2551-2556.
[4] Alciatore D,Ng C.Determining manipulator workspace boundaries using the Monte Carlo method and least squares segmentation[C]//23rd ASME Mechanisms conference,1994:141-146.
[5] 曹毅,李秀娟,宁祎.三维机器人工作空间及几何误差分析[J].机械科学与技术,2006,25(12):1458-1461,1502.
[6] 印峰,王耀南,余洪山.基于蒙特卡罗方法的除冰机器人作业空间边界提取[J].控制理论与应用,2010,27(7):891-896.
[7] Wenbin Chen,Caihua Xiong,Xiaolin Huang,et al.Manipulator Workspace Boundary Extraction and Its Applicationin Workspace Analysis of the Human’s Upper Extremity[J].Advanced Robotics,2009,23(10):1393-1410.
[8] Klopcar N,Tomsic M,Lenarcic J.A kinematic model of the shoulder complex to evaluate the arm-reachable workspace[J].Journal of Biomechanics,2007,40(1):86-91.
[9] 杨丹,赵海滨,龙哲.MATLAB图像处理实例详解[M].清华大学出版社,2013.
[10] 吴一全,宋昱,周怀春.基于各向异性数学形态学的火焰图像边缘检测[J].仪器仪表学报,2013,34(8):1818-1825.
[11] 彭智浩,杨风暴,王志社,等.基于数学形态学和自动区域生长的红外目标提取[J].红外技术,2014(1):47-52.
[12] 赵明波,何峻,田军生,等.基于改进的渐进多尺度数学形态学的激光雷达数据滤波方法[J].光学学报,2013(3):285-294.
[13] 黄海龙,王宏,郭潘,等.一种基于数学形态学的多形状多尺度边缘检测算法[J].东北大学学报:自然科学版,2010,31(10):1483-1486.
[14] 张伟伟,刘学峰.基于数学形态学的图像边缘检测研究[J].计算机与数字工程,2006,34(9):59-60.
[15] 沈世旻,盛翊智.基于边缘检测的车牌图像分割技术[J].自动化技术与应用,2004,23(3):24-26.
[16] Maragos P.Tutorial on advances in morphological image processing and analysis[J].Optical Engineering,1987,26(7):623-632.
A MANIPULATOR WORKSPACE BOUNDARY EXTRACTION ALGORITHM
Li YuanfengZhang Wanxin
(National Key Laboratory of Human Factors Engineering,China Astronauts Research and Training Center,Beijing 100094,China)
The boundary extraction of workspace is a significant operation in design and performance evaluation of actuator such as manipulators. In the paper we transform the point cloud of manipulator workspace to image, and propose a novel manipulator workspace boundary extraction algorithm in combination with greyscale image processing method. First we define the grid density algorithm, which is employed as the transform operator for transforming the point cloud to greyscale image. Grid density describes the distribution status of space point cloud, and can be used to analyse the dexterity of manipulators. Then we use mathematical morphology processing method to smooth the greyscale image and detect its boundary. Finally, by making use of the coordinate correspondence we obtain the coordinates location information of boundary through backcalculation. The accessible domain of human’s upper extremity is taken as the experimental object to verify the proposed algorithm, result indicates that the novel algorithm is fast and accurate in the extraction of accessible domain of human’s upper extremity, and has the advantages in operation speed and accuracy than some other algorithms.
ManipulatorWorkspaceBoundary extractionGrid densityMathematical morphology
2015-02-03。载人航天领域预先研究项目(040301)。李元丰,硕士生,主研领域:航天服工程。张万欣,研究员。
TP30
A
10.3969/j.issn.1000-386x.2016.09.047

