一个新的具有非单调零齐次核的Hilbert型不等式

钟建华，陈　强

(1．广东第二师范学院 数学系， 广东 广州 510303；2．广东第二师范学院 计算机科学系， 广东 广州 510303)



一个新的具有非单调零齐次核的Hilbert型不等式

钟建华1，陈强2

(1．广东第二师范学院 数学系， 广东 广州 510303；2．广东第二师范学院 计算机科学系， 广东 广州 510303)

引入一个新的非单调且零齐次的核,利用含参数σ的权函数及配方方法,得到了相应的具有最佳常数因子的Hilbert型积分不等式及其等价形式,并给出了特殊情形.

Hilbert型不等式；权函数；参数；等价式

0　引言

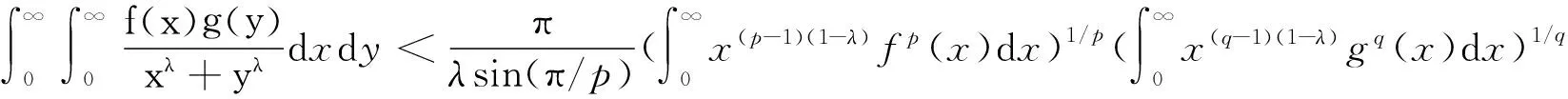
(1)

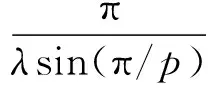
研究核为负齐次的Hilbert型不等式是近年来该研究领域中对经典不等式进行推广的一个主要突破点,在Hilbert型不等式参量化研究体系中至关重要.关于核为负齐次的Hilbert型不等式的一般性理论可参见文[2].

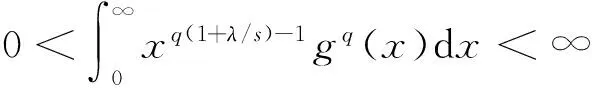
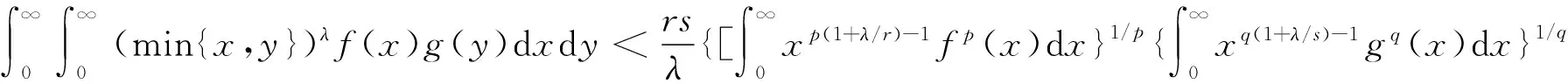
(2)

文[4]得到一个特殊的核为实数齐次的Hilbert型积分不等式,引入参数λ≥0,在右边积分为正数的条件下,有

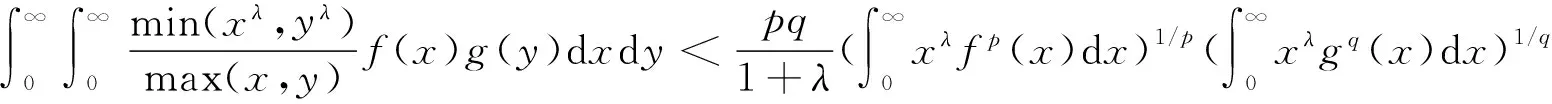
(3)

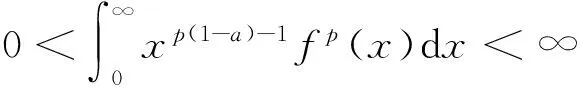
(4)

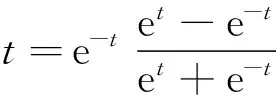
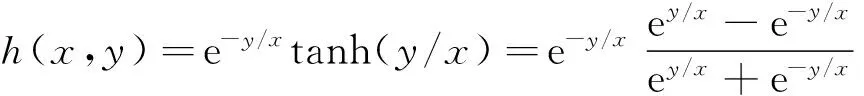
(5)

应用权函数及实分析方法,建立一个具有最佳常数因子的零齐次核的Hilbert型积分不等式和等价式,并考虑了一些特殊结果.

1　一些引理

(6)

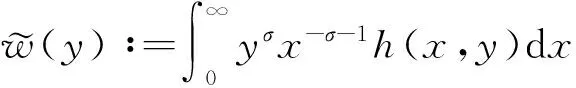
(7)

则有

(8)

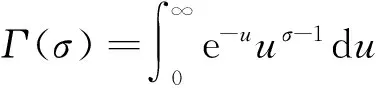
证明对式(6)作变换u=y/x,则有

(9)

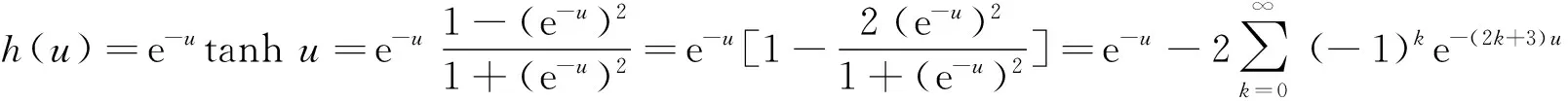
将其代入式(9)中,并令t=(2k+3)u,得

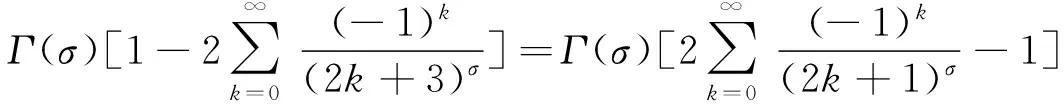
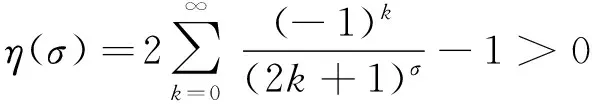
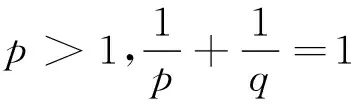
(10)

这里,k(σ)为式(8)所定义.

证明配方并由Hölder不等式[8]及式(7),有

(11)

由式(11),Fubini定理[9]及式(6),式(7),有

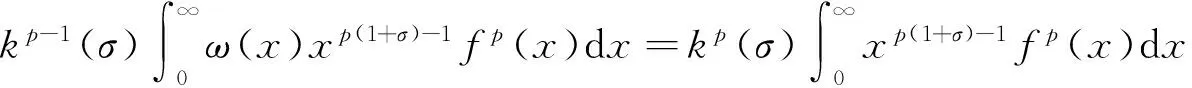
即式(10)成立.证毕.

2　主要定理

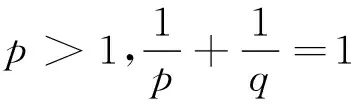
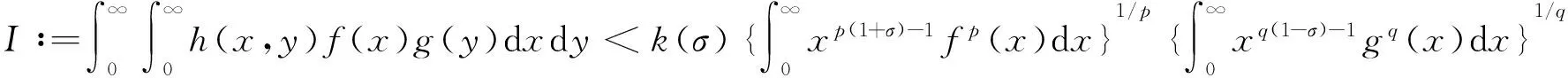
(12)

(13)

这里,k(σ)为式(11)所定义,且k(σ)及kp(σ)均为最佳值.

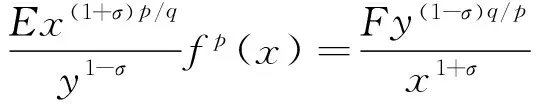
不妨设E≠0(否则,F=E=0),故有

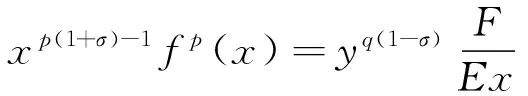
配方并由Hölder不等式[8],有

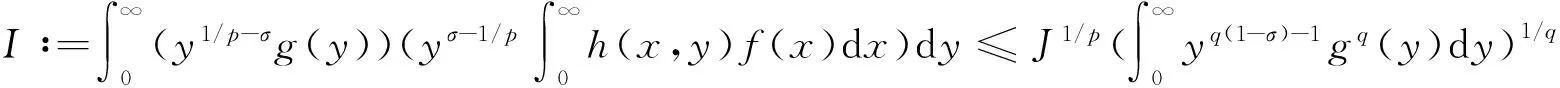
(14)

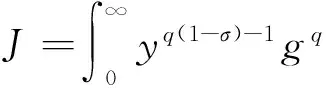
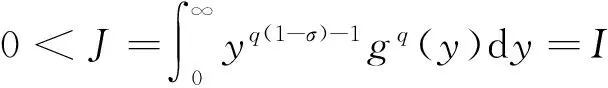
(15)

即

(16)

对式(16)两边p次方,可得式(13),且它与式(12)等价.

则可算得

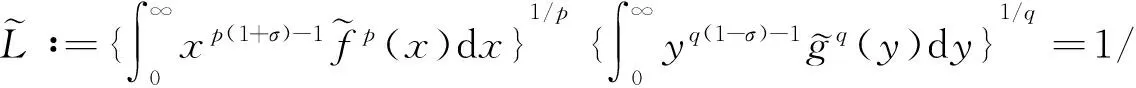
由Fubini定理[9],并对下式中的内积分作变换u=y/x,可得

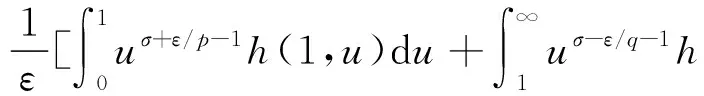
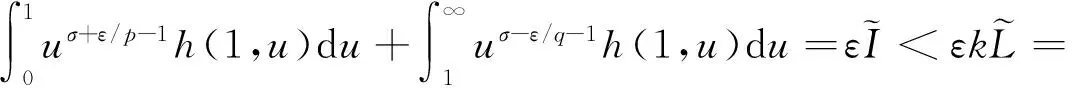
(17)

由Fatou引理[9],及式(17),易得

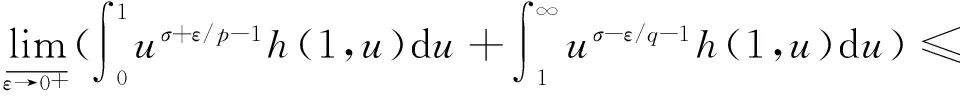
这与假设矛盾,故k=k(σ)必为式(12)的最佳值.式(13)的常数因子kp(σ)必为最佳值,不然,由式(14),必导出式(12)的常数因子也不为最佳值的矛盾结论.证毕.

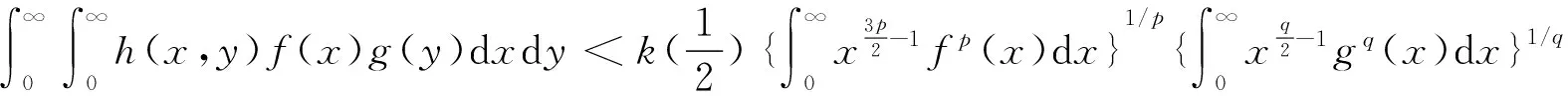
(18)

(19)

(20)

(21)

致谢：作者衷心感谢杨必成教授的细心指导.

[1] 杨必成. 关于一个推广的Hardy-Hilbert不等式[J].数学年刊(A),2002,23(2):247-252.

[2] 杨必成.算子范数与Hilbert型不等式[M].北京:科学出版社,2009:148-299.

[3] 杨必成.关于正数齐次核的Hilbert型不等式[J].广东教育学院学报,2009,29(3):1-8.

[4] 杨必成.一个Hilbert型积分不等式[J].浙江大学学报(理学版),2007,34(2):121-124.

[5] 杨必成.一个新的零齐次核的Hilbert型积分不等式[J].浙江大学学报(理学版),2012,39(4):390-392.

[6] 王竹溪,郭敦仁.特殊函数概论[M].北京:北京大学出版社,2000:40-81.

[7] 钟玉泉.复变函数论[M].北京:高等教育出版社,2003.

[8] 匡继昌. 常用不等式[M].济南:山东科学技术出版社,2004:4-5.

[9] 匡继昌. 实分析引论[M].长沙:湖南教育出版社,1996:45-46.

A New Hilbert-Type Inequality with the Non-monotone Homogeneous Kernel of Degree 0

ZHONG Jian-hua1, CHEN Qiang2

(1． Department of Mathematics, Guangdong University of Education, Guangzhou,Guangdong, 510303, P.R.China; 2． Department of Computer Science, Guangdong University of Education, Guangzhou, Guangdong, 510303, P.R.China)

A new Hilbert-type inequality with the non-monotone homogeneous kernel of degree 0 is provided in this paper. By utilizing the weight coefficients with the parameter σ and the method of completing the square, the corresponding Hilbert-type integral inequality with the best constant factor and the equivalent form are obtained. Some particular cases are considered.

Hilbert-type inequality; weight function; parameter; equivalent form

2015-09-28

国家自然科学基金资助项目(61370186)；2014年广州市科技计划应用基础研究项目(2014J4100032)

钟建华,男, 广东廉江人, 广东第二师范学院数学系副教授.

O178

A

2095-3798(2016)05-0038-05