一类具记忆项的二阶非线性发展方程的能量衰减估计

吴佳睿，蒲志林

（四川师范大学　数学与软件科学学院，成都 610066）

一类具记忆项的二阶非线性发展方程的能量衰减估计

吴佳睿，蒲志林

（四川师范大学数学与软件科学学院，成都 610066）

主要研究一类具有记忆项的二阶非线性发展方程的能量衰减估计，通过运用积分不等式以及索布列夫空间嵌入定理，证明该方程柔和解的能量呈指数衰减。

全局存在性；指数衰减；非线性波方程；积分微分方程

0 引 言

设Ω⊂Rn是具有光滑边界Γ的有界区域，考虑以下的粘弹性膜方程：

问题（1）描述的是具记忆项的材料力学问题。其中γ是正常数，△是拉普拉斯算子，β称为记忆项。文献［1-3］通过Lyapunov方法研究了方程（1）的某种扰动能量，得出了解的存在性及能量衰减性质，文献［4］研究了方程（1）的原始能量，得出了能量的衰减估计，但添加了对记忆项的限制：β（0）＞0，β′（t）≤0，。本文弱化了限制条件，使其结果可运用到更广泛的情况。

为此考虑抽象空间X（X是一个Hilbert空间）上的抽象方程：

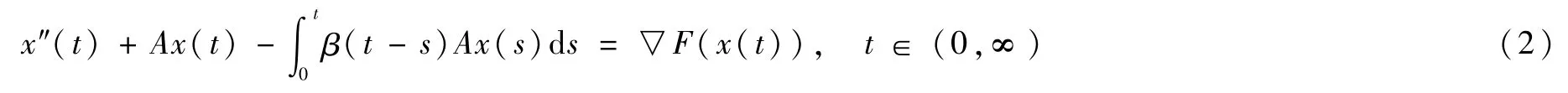
其中A=-△是自共轭线性算子，并且在其定义域稠密。▽F是Gâteaux可微泛函F的梯度算子。

本文的主要目的是在对记忆项β具有更弱的限制条件下，对方程（2）的能量作出衰减估计。这个弱化的限制条件是：

β∶［0，∞）→［0，∞）是局部绝对连续函数，且存在α（t）≥0，使得下列条件满足：

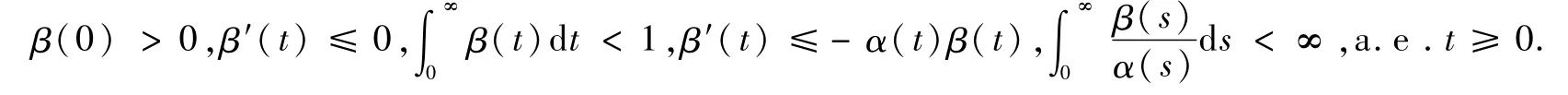
为了方便研究，下面一节将介绍必要的预备知识与基本假设，最后将给出文章的主要结论及证明。

1 预备知识与基本假设

假设X是一实H ilbert空间，内积记为〈·，·〉，范数记为‖·‖，L1（0，T）是通常的取实值的Lebegue空间。对任意f∈L1（0，T）和任意的

考虑下列抽象二阶微分方程：

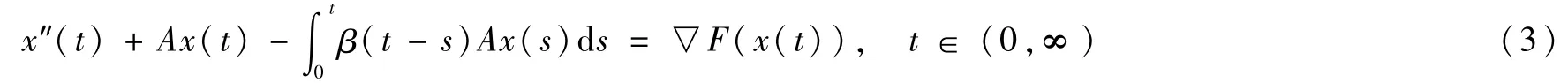
作以下假设：

（H1）A在 X上是自共轭线性算子，D（A）是稠密的，∃M ＞0使得

（H2）β∶［0，∞）→［0，∞）满足：

（b）存在函数 α（t）≥0使得

（c）∀R＞0，∃常数CR＞0使得有

（d）F（0）=0，▽F（0）=0，且存在一个严格单调递增的连续函数 ψ∶［0，∞）→［0，∞）使得：

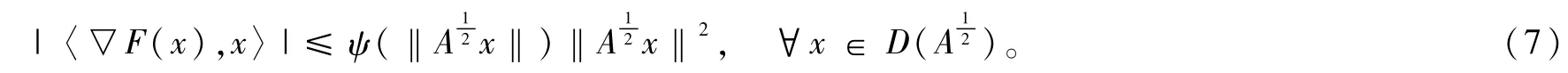
假设x0，x1∈X，考虑柯西问题：

引 理1［5，6］若x0∈D（），x1∈X，T＞0，则方程（8）在［0，T］上存在唯一的柔和解x，并且x∈C1（［0，T］；X）。如果x0∈D（），x1∈D（），则方程（8）的柔和解也是强解，并且x∈C1（［0，T］；D（））。

根椐文献［7］，我们把方程（8）的能量定义为：

引理2［4］在假设（H1-H3）下，方程（8）的能量 Ex（t）单调递减，并且：

则存在ρ0＞0，使得当x0∈D（），x1∈X，且

引理3［4］若假设（H1-H3）成立，并且存在一严格递增的连续函数 ψ∶［0，∞）→［0，∞），使得时，能量Ex满足：

注：假设（7）确保了条件（10）的成立。

引理 4［8-11］假设Ex在［0，∞）上是非负的单调递减函数，如果∃常数S0，C＞0，使得

2 主要结论及证明

定理1 若假设（H1-H3）成立，且S0＞0，则存在正数ρ0和 C，使得当 x0∈D（A），x1∈X且时，方程（8）的柔和解x的能量Ex（t）满足：

定理2 若假设（H1-H3）成立，则存在正数ρ0和 C，使得当x0∈D（A），x1∈X且ρ0时，方程（8）的柔和解x的能量Ex（t）满足：Ex（t）≤Ex（0）exp（1-Ct），∀t≥0。

定理1的证明：

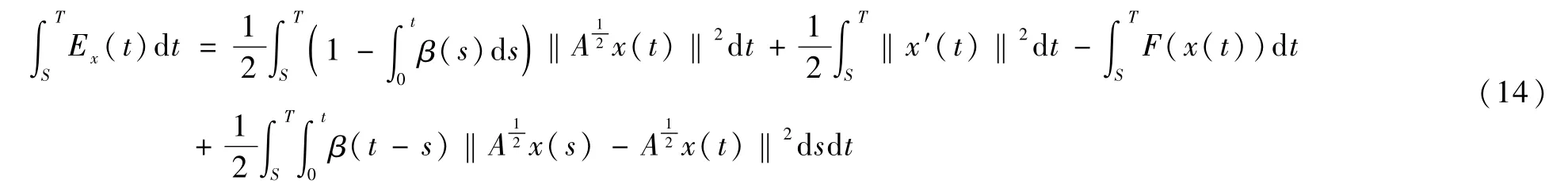
下面先对方程（14）右边第一项进行估计，用x（t）与方程（3）作内积再在（S，T）上积分，可得：

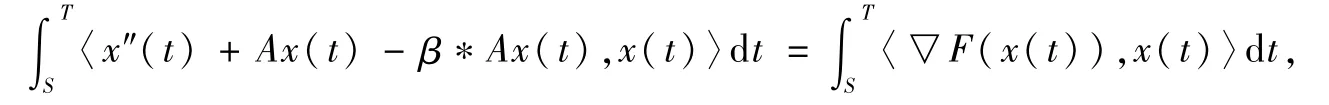
即有：

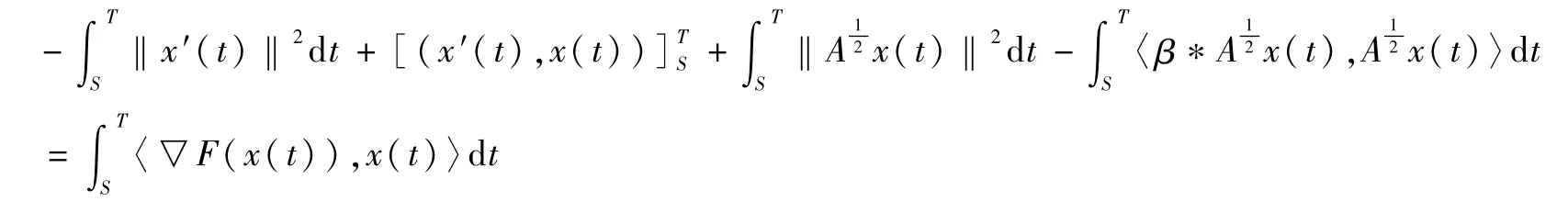
因此可得：

下面对（15）右边第三项进行估计，注意到对任意的ε＞0，有：

而根椐条件（5）和（9），我们有：

定理1得证，再结合引理4，定理2显然成立。

［1］BERRIM IS，MESSAOUDIS A.Existence and decay of solutions of a viscoelastic equation with a nonlinear source［J］.Nonlinear Analysis：Theory，Methods and Applications，2006，64（4）：2314-2331.

［2］CAVALCANTIM M，OQUENDO H P.Frictional versus viscoelastic damping in a sem ilinear wave equation［J］.SIAM JControl Optim，2003，42（4）：1310-1324.

［3］KOMORNIK V，ZUAZUA E.A directmethod for the boundary stabilization of the wave equation［J］.JMath Pures Appl.，1990，69（1）：33-54.

［4］ALABAU-BOUSSOUIRA F，CANNARSA P，SFORZA D.Decay estimates for second order evolution equations with memory［J］.Journal of Functional Analysis，2008，254（5）：1342-1372.

［5］PRÜSS J.Evolutionary Integral Equations and Applications［M］.Basel：Birkhauser-Verlag，1993.

［6］CANNARSA P，SFORZA D.Mathematical Models and Methods for Smart Materials［M］.Bologna：World Scientific，2002：343-345.

［7］RIVERA J E M，SALVATIERRA A P.Asymptotic behaviour of the energy in partially viscoelastic materials［J］.Quart Appl Math，2001，59（3）：557-578.

［8］ALABAU-BOUSSOUIRA F.A general formula for decay rates of nonlinear dissipative systems［J］.Comptes Rendus Mathematique，2004，338（1）：35-40.

［9］ALABAU-BOUSSOUIRA F.Convexity and weighted integral inequalities for energy decay rates of nonlinear dissipative hyperbolic systems［J］.Appl Math Optim，2005，51（1）：61-105.

［10］ELLER M，LAGNESE JE，NICAISE S.Decay rates for solutions of a Maxwell system with nonlinear boundary damping［J］. Comput.Appl.Math，2002，21（1）：135-165.

［11］MARTINEZ P.A new method to obtain decay rate estimates for dissipative systems［J］.ESAIM Control Optim CA，1999，4（1）：419-444.

The Energy Decay Estimates for General Second Order Nonlinear Evolution Equations w ith M emory

WU Jiarui，PU Zhilin
（College of Mathematic and Software Science，Sichuan Normal University，Chengdu 610066，China）

The paper studied the energy decay estimates for general second order nonlinear evolution equations with memory.Based on the integral inequality and Sobolev embedding theorem，it has been confirmed that the energy of m ild solution decays with exponential rate.

global existence；exponential decay；nonlinear wave equations；integro-differential equations

O19

A

10.16246/j.issn.1673-5072.2016.01.002

1673-5072（2016）01-0010-07

2016-03-02

四川省科技计划项目（2015JY0125）

吴佳睿（1990—），女，四川成都人，硕士，主要从事偏微分方程稳定性研究。E-mail：287694855@qq.com

蒲志林（1963—），男，四川万源人，博士，教授，博士生导师，主要从事非线性微分方程与无穷维动力系统理论研究。E-mail：411296267@qq.com