多轮独立电驱动车辆驱动力优化控制研究
阳贵兵,廖自力,马晓军,刘春光
(装甲兵工程学院陆战平台全电化技术重点实验室,北京100072)
多轮独立电驱动车辆驱动力优化控制研究
阳贵兵,廖自力,马晓军,刘春光
(装甲兵工程学院陆战平台全电化技术重点实验室,北京100072)
为了充分发挥多轮独立电驱动车辆的动力性能,提出了一种层次化的驱动力优化控制结构。该控制结构包含基于各轴载荷预分配控制、驱动防滑控制和基于车辆状态的再分配3层控制,其中防滑控制是核心层,采用基于路面最优滑转率滑模控制的方法,通过设计基于累积求和统计目标控制的路面跳变检测器,结合车轮滑转率-路面附着系数图形,可实现变路面的最优滑转率估计。通过该分层控制结构,实现了驱动力在各轴之间以及各个驱动电机之间的优化分配控制。利用硬件在环实时仿真实验验证了该控制结构能改善车辆的爬坡性能、直线加速性能以及障碍路面行驶的通过性。
控制科学与技术;多轮独立电驱动;动力性能;驱动防滑;优化控制
DOI:10.3969/j.issn.1000-1093.2016.01.004
0 引言
相比传统机械传动车辆,多轮独立电驱动车辆具有全轮独立可控、电机转矩响应快速以及输出转矩可精确测量等优势[1]。基于这些优势,许多学者开展了轮毂电机驱动车辆牵引力控制研究[2-4],以及行驶稳定性控制研究[5]。
牵引力控制系统,是目前应用较为广泛地用于提高轮毂电机驱动车辆直驶动力性能和稳定性能的控制系统,其主要通过驱动防滑控制(ASR)来实现[6-7]。但由于ASR是针对单轮实施控制的,只能实现单个驱动轮的最优转矩输出控制,而无法实现整车层面的多电机协调控制,即在驾驶员给定一定的情况下,无法实现转矩在驱动电机之间的转移,因此,容易出现整车牵引力降低,动力性能不能完全发挥的缺点。
针对以上不足,本文以ASR为核心,增加了基于载荷预分配和基于车辆状态的再分配的转矩优化控制策略,实现整车驱动力的优化分配控制。ASR控制中,最优滑转率采用路面附着系数μ-车轮滑转率λ曲线斜率法获得,并设计基于累积求和(CUSUM)统计目标控制法的路面跳变监测器,实现变路面的最优滑转率估计,在此基础上,利用滑模变结构控制算法计算最优输出转矩。最后,利用硬件在环实时仿真平台对所提出的控制方案进行仿真分析和验证。
1 整车驱动力优化控制策略
整车驱动力控制结构如图1所示,最上层为基于各轴载荷的预分配,中间层为防滑控制,最下层为驱动力再分配,控制器直接控制对象为8个驱动电机。各控制层所需要的车辆状态参数通过传感器获取,主要状态参数包括纵向加速度aχ、车轮转速ωi和车速v,其中,车速采用估计的方法获取。Trefi_1,…,Trefi_8为第i层控制输出的给定转矩;Tref1,…,Tref8为8个驱动电机实际输出的转矩值。
2 基于各轴载荷的驱动力预分配
车辆在爬坡和加速行驶情况下,各轴载荷分配不均匀,在相同路面附着条件下,各轮所能获得的最大路面附着力也不同,如果采用转矩平均分配的方法,虽然可以保证车辆行驶的平稳性,但由于载荷小的车轮无法输出期望的扭矩,整车的驱动力将会受到影响,车辆动力性能不能完全发挥。因此,本文提出了基于各轴载荷的驱动力预分配方法。转矩预分配层中,包含油门踏板信号解析和载荷计算两部分。
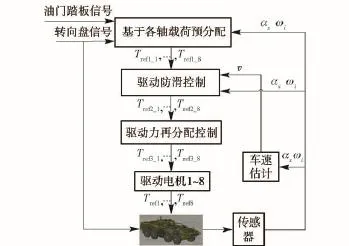
图1 整车驱动力优化控制框图Fig.1 The control structure of vehicle driving force
2.1 油门信号解析
轮毂电机驱动车辆的油门踏板信号不再等同传统车辆发动机的齿杆位置,而是代表轮毂电机的转矩。为了符合驾驶员的操作感觉,油门踏板设立了自由行程和有效行程,油门踏板开度η可表示为
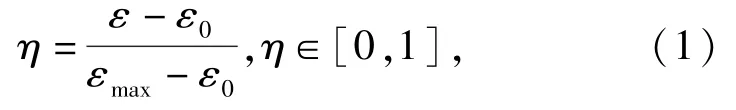
式中:ε0、ε和εmax分别表示油门踏板的空行程、有效行程和最大行程。
油门踏板开度η与总需求转矩Ttot的关系为
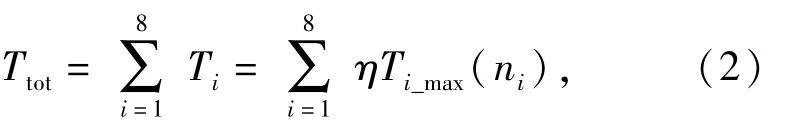
式中:Ti_max(ni)为第i个电机在当前转速下的最大转矩。电机的外转矩特性曲线关系如图2所示。
2.2 各轴载荷计算
假设车辆在坡度为α的坡面上直线加速行驶,车辆受力分析如图3所示。
图3中,Ff为车辆爬坡阻力,包括风阻、车轮滚动阻力等;Fd表示整车驱动力;H为质心高度;Fzi为第i轴载荷,Li为第i轴到第1轴的距离;L0为第1轴到质心的距离;a为车辆加速度。
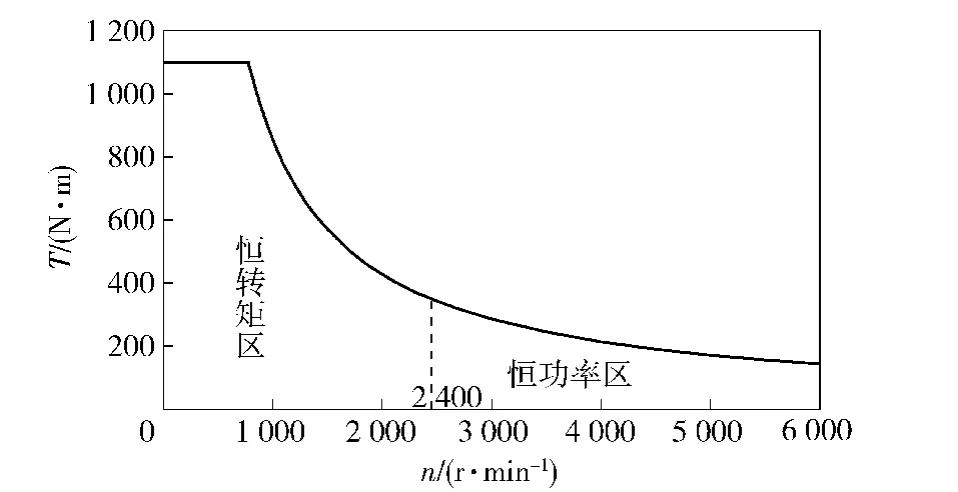
图2 电机外转矩特性曲线Fig.2 Characteristic curve of motor torque
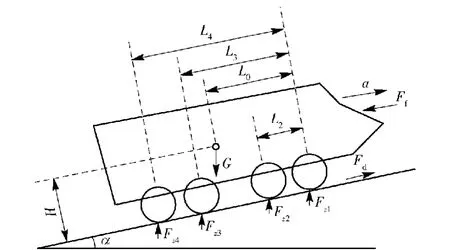
图3 车辆爬坡受力分析Fig.3 Force analysis of vehicle climbing
各轴车轮载荷计算[8]如下:
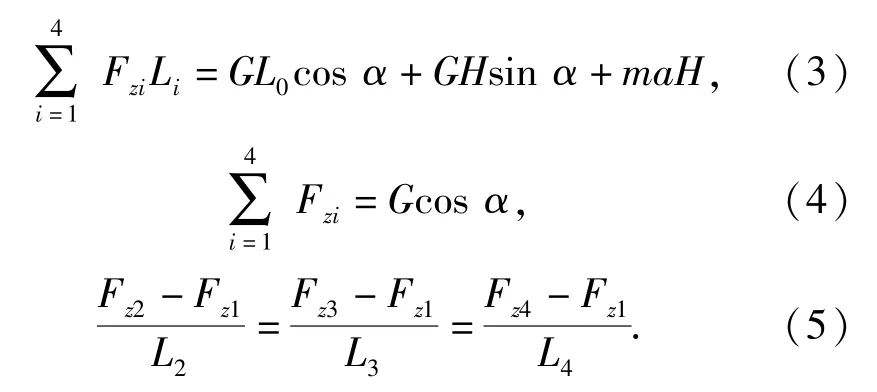
根据(3)式~(5)式可得到各轴载荷为
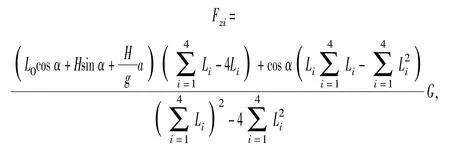
则各轴驱动电机预分配的转矩值(同轴两侧驱动电机预分配值相同)为
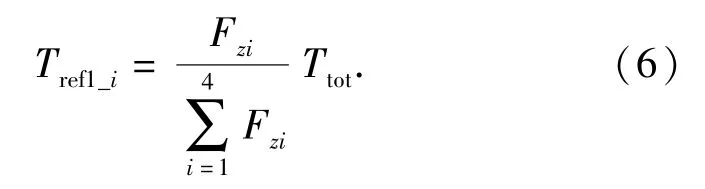
3 驱动防滑控制
当车辆在低附着路面加速、不平路面行驶或者过沟坎等工况时,经常会出现部分车轮打滑甚至悬空的情况,根据以往的仿真经验,在这些工况下,单纯依赖基于载荷的转矩分配方法,无法有效克服车轮打滑的现象,而车轮的过度滑转,一方面会影响车辆行驶的稳定性,另一方面降低了车辆的动力性能。因此,本文在基于载荷的转矩预分配后,增加驱动防滑控制层,对8个驱动轮进行独立控制,防滑控制结构如图4所示。
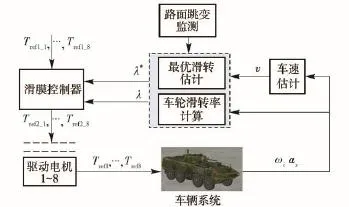
图4 驱动防滑控制结构Fig.4 The control structure of ASR
图4中,ASR主要包括最优滑转率估计,车轮滑转率计算、路面跳变监测以及滑模控制器4个部分,λ和λ*分别表示轮胎的滑转率和最优滑转率,滑模控制器根据输入的轮胎滑转率和最优滑转率值,输出端为8个电机的转矩优化值。
3.1 最优滑转率估计
最优滑转率估计是驱动防滑控制的关键技术,滑转率估计的准确与否直接决定了防滑控制的效果。本文提出了一种对μ-λ曲线求斜率的方法估计最优滑转率点,并采用CUSUM统计目标控制法实现变路面行驶工况下的最优滑转率估计。
图5给出了3种路面下的车轮滑转率λ与路面附着系数μ的关系曲线,从中可以看出,路面附着系数随车轮滑转率总是先增加再减少,路面附着系数最大值所对应的滑转率称为最优滑转率。因此,可以通过对路面附着系数求滑转率的微分,通过观察其值的正负变化确定最优滑转率点。
根据(7)式:
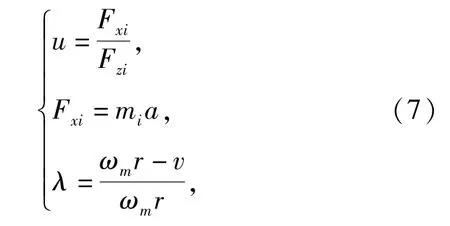
可推导出:
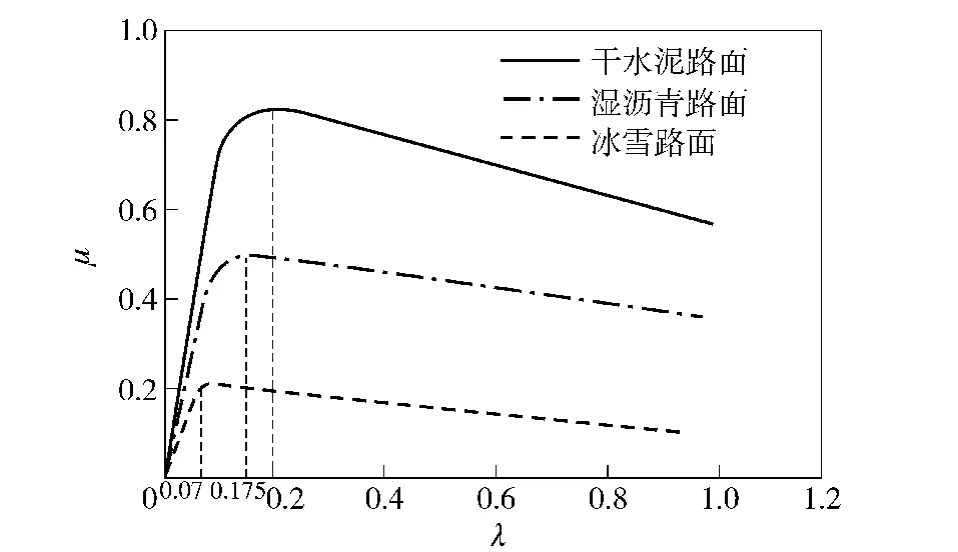
图5 3种典型路面的μ-λ关系曲线Fig.5 μ-λ curves of three typical road surfaces
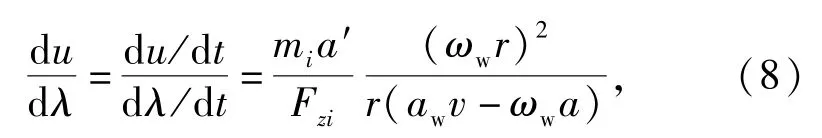
式中:Fχi、Fzi表示第i轴车轮的驱动力和载荷;mi表示整车质量在第i轴的分量;ωw为车轮转速;aw为车轮加速度;r为车轮半径。
du/dλ值的变化跟式a'(awv-ωwa)有关,式中的变量a和ωw可以通过加速度传感器和转速传感器获取,车速v通过a与ωw值进行估算得到,传感器信号的准确度直接影响到du/dλ值的计算,因此,在使用之前,需对采集到的传感器信号进行滤波处理。
当车辆行驶路面发生变化,车轮滑转率也会随之发生改变,所对应的最优滑转率值也发生变化,此时,前一个估算周期所获得的最优滑转率值显然已经不能适用,控制器需要对λ*重新进行估计,本文采用CUSUM统计目标控制法,设计路面跳变监测器,其原理如下:
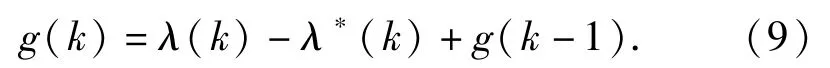
当路面条件无变化时,测量得到的λ(k)应在估计出的最优滑移率λ*(k)附近,因而g(k)的累积求和应在零值附近波动。若路面确实发生了跳变,车轮滑转率也会随之跳变,因此,会出现λ(k)总是大于或者小于λ*(k),通过设置阀值H,当g(k)累计值超过H时,可以认为路面发生了跳变。H值的大小直接决定了监测器的敏感度,H设置过小,则会造成频繁的触发,H设置过大,则会降低检测的精度。
g(k)会出现正、负两种累计值,因此,必须设置正、负两个阀值。当g(k)超过正值H时,即λ持续大于λ*,这种情况说明车轮进入附着系数更低的路面行驶,此时,应在前一个估算周期得到的λ*控制基础上,进一步减小电机转矩输出,同时,采用μ-λ曲线斜率法再一次对最优滑转率值进行估算,并用其估算的结果对监测器中的λ*值进行更新。当g(k)低于负值H时,即λ持续小于λ*,这种情况出现有两方面原因:一是车轮进入高附着系数路面行驶,另外就是驾驶员降低了油门踏板给定。此情况下,防滑控制器放开电机转矩输出限制,待μ-λ曲线出现新的斜率拐点时,再重新进行控制。
3.2 滑模控制器设计
在获得当前路面最优滑转率值的基础上,采用基于最优滑转率滑模控制方法对电机输出转矩进行控制。
车辆在水平路面时的车轮模型为
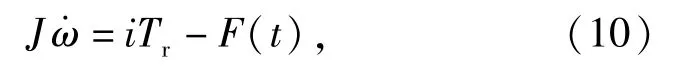
驱动电机简化为1阶动态系统模型:
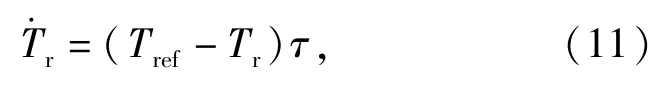
式中:J为车轮转动惯量;i为传动比;Tr为电机实际输出转矩值;F(t)为轮胎所受的地面附着力和滚动阻力之和;Tref为电机转矩参考值;τ为电机相应时间常数。
令χ1=ω,χ2=Tr,建立系统状态方程:
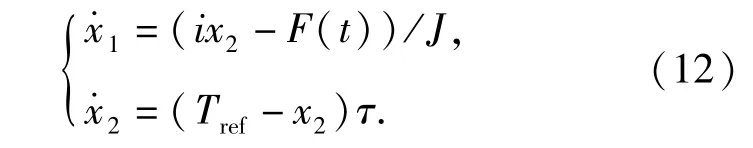
选取两个线性滑模面:

式中:χ1d、χ2d分别为最优滑转率点所对应的电机转速的期望值和实际输出转矩的期望值。
选择指数趋近率:
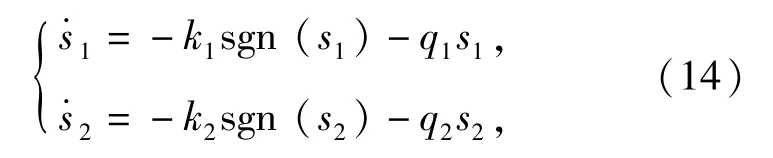
式中:k1>0,q1>0,k2>0,q2>0.k1、k2值决定了趋近的速度,其值越大,趋近的速度越快,但是可能导致到达滑模面后出现比较大的抖振;通过调节q1、q2值可有效保证非滑模运动具有良好品质。因此,在参数选择时,可适当增大q1、q2值,减小k1、k2值。
将(13)式代入(14)式得
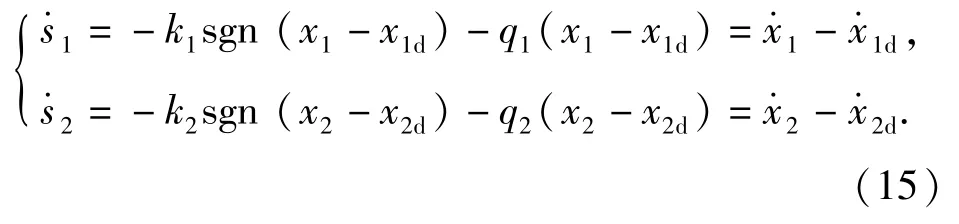
联立(12)式得
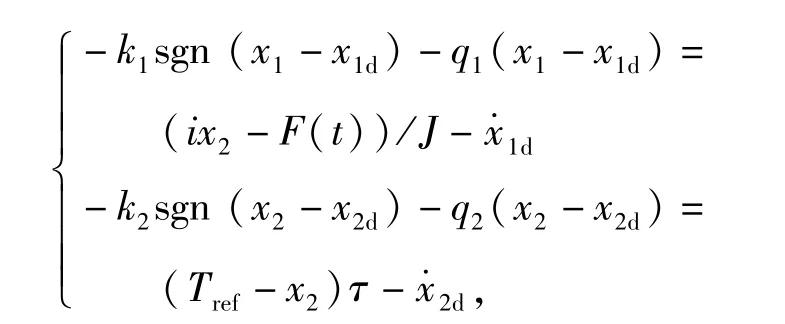
消除χ2,得
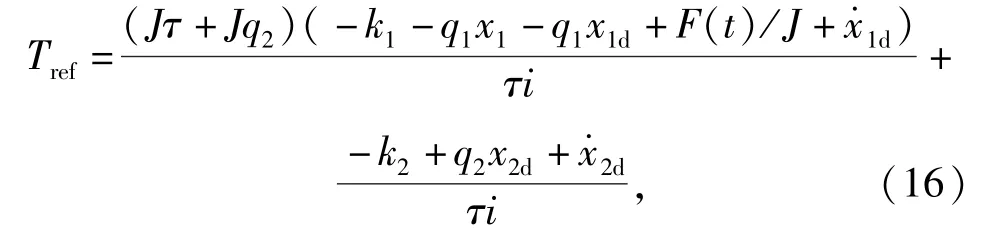
Tref即为给定的电机转矩参考值,通过对每个车轮进行防滑控制,可得到8个驱动电机参考值输出Tref2_1,…,Tref2_8.
4 基于状态的驱动力再分配控制
与机械车辆不同,轮毂电机驱动装甲车辆驱动力控制除实现防滑控制外,还可以实现驱动力的再分配控制:当出现个别车轮的滑转后,由于实施防滑控制所降低的该车轮转矩可以增加到其他正常车轮上,以维持整车驱动力不变。本文采用基于车辆行驶状态的驱动力再分配控制,分配策略如下:
以左侧车轮的为例,首先判断车轮是否出现滑转状况,并计算因滑转而损失的驱动力:
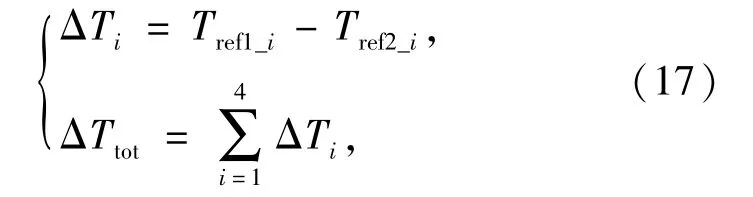
式中:Tref1_i表示基于载荷预分配层给定的第i个电机转矩;Tref2_i为防滑控制层输出的该电机给定转矩;当ΔTi值大于某一阀值时,则可判断出该车轮是否发生了滑转;ΔTtot表示左侧4个车轮因滑转而减少的总驱动力。
其次,计算该侧各驱动电机的转矩再分配值:
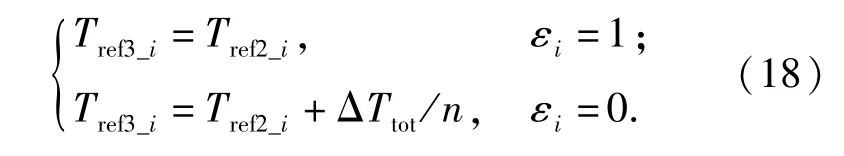
式中:εi=1表示第i个车轮有滑转;εi=0表示该车轮正常;n表示正常的车轮数量。
5 硬件在环联合仿真实验分析
本文采用基于实车中央控制器的硬件在环实时仿真实验对所提出的驱动力优化分配算法进行验证分析,硬件在环实时仿真平台结构如图6所示。
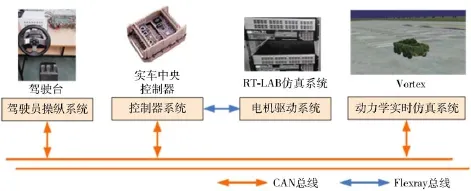
图6 硬件在环实时仿真平台Fig.6 Hardware-in-loop real-time simulation platform
其中车辆动力学模型以及路面场景模型采用多体动力学仿真系统Vortex软件进行建模。本文研究对象为8轮独立驱动车辆,车辆动力学模型全质量21 t,包括车身模型、悬架、转向机构以及轮胎模型4个部分,其中,轮胎模型采用Magic轮胎模型。路面场景模型根据仿真需要采用三维实体建模,并可设置不同的路面附着系数,能充分反应轮-地相互作用力。
5.1 爬坡性能仿真分析
车辆爬30°坡实验,主要验证基于载荷分配各轴转矩的策略对车辆爬坡性能的影响,采用平均分配各轴转矩作为对比实验,仿真路面附着系数设置为0.8,油门踏板满程。仿真结果如图7、图8所示。
车辆在平路开始加速,在第8 s接触坡面,第8.5 s车辆完全行驶在坡面上,第24 s完成爬坡。油门踏板给定的总驱动力矩峰值为8 800 N·m.采用平均分配法,各轴每个电机给定转矩相同,峰值为1 100 N·m;而采用基于载荷飞分配,从第1到第4轴转矩峰值分别为420 N·m、900 N·m、1 300 N·m、1 780 N·m.由仿真结果可知,采用平均分配各轴转矩,由于前两轴载荷较小,车轮能够利用的最大路面附着力小于轮边扭矩的期望值,车轮发生滑转,电机输出转矩降低,整车牵引力不足,因此,车辆在坡面上处于减速状态,最后速度降为0;而采用本文基于载荷分配转矩的方法,车辆能以15 km/h的稳定车速完成爬坡。
5.2 单一附着路面行驶仿真
低附着路面加速仿真:路面附着系数设置为0.3,油门踏板满程。仿真结果如图9~图12所示。
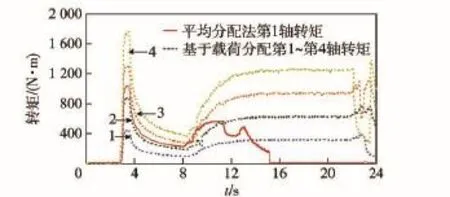
图7 电机输出转矩Fig.7 Motor torque output
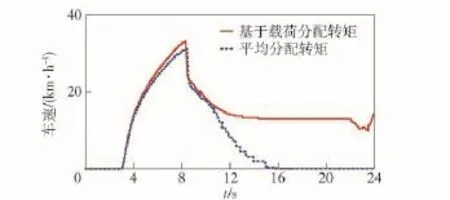
图8 车速曲线Fig.8 The curves of vehicle speed
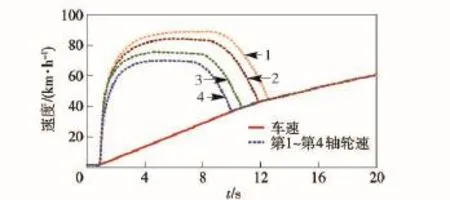
图9 无控制时车速与左侧4轮转速Fig.9 The vehicle speed and the 4-wheel speed on the left side without control
该附着路面条件下估计出的最优滑转率为0.12,防滑控制器通过控制驱动电机的转矩,将车轮滑转率控制在最优滑转率附近,减小了车轮的滑转,最终仿真车速达到78 km/h,而无控制状态最终车速为60 km/h,采用防滑控制使车辆的动力性能得到提高。
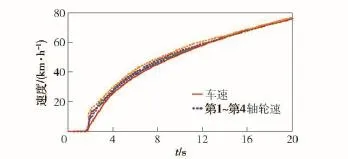
图10 无控制时车速与左侧4轮转速Fig.10 The vehicle speed and the 4-wheel speed on the left side without control
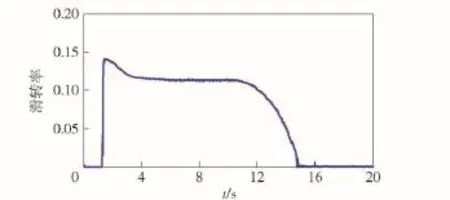
图11 第1轴左侧车轮滑转率Fig.11 The wheel slip ratio on the left side of the first axis
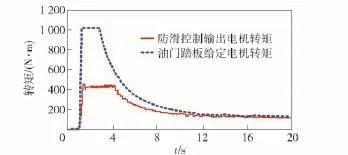
图12 第1轴左侧电机输出转矩Fig.12 The motor torque on the left side of the first axis
5.3 变路面仿真
5.3.1 低附着与高附着对接路面加速行驶
车辆在低附着与高附着对接路面加速行驶,踏板行程满程,低附着路面附着系数设置为0.3,高附着路面附着系数设置为0.8.车辆在第4 s由低附着路面进入高附着路面,以第1轴左侧车轮为观测对象。仿真结果如图13、图14所示。
在低附着路面行驶时,防滑控制器以0.12的滑转率为最优控制目标调节驱动电机的转矩,从第4 s进入高附着路面后,路面跳变检测器检测到路面跳变,并对最优滑转率进行重新估计,估计值为0.185,防滑控制器迅速调节电机转矩的输出值。
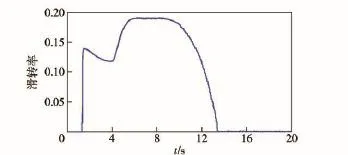
图13 车轮滑转率Fig.13 The wheel slip ratio
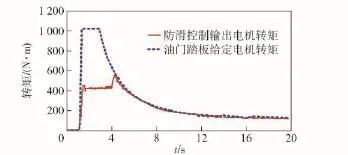
图14 电机输出转矩Fig.14 Motor torque output
5.3.2 过连续起伏路面仿真
选择连续起伏障碍路面,路面附着系数设置为0.9,由于车辆在起伏路面行驶时,各驱动轮的载荷发生连续变化,甚至会出现车轮悬空,因此,可看做是路面附着系数变化的行驶条件。以第1轴左侧车轮为观测对象,仿真结果如图15~图17所示。
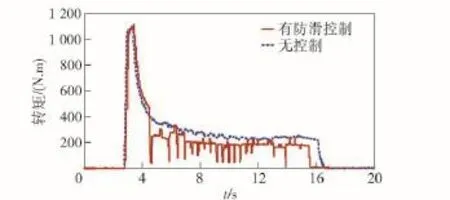
图15 电机输出转矩Fig.15 The motor torque output
车辆从第4.5 s开始进入连续起伏路面,在起伏路面行驶过程中,最优滑转率估计值介于0.075~0.2之间(车轮悬空的时候为0.075,与路面接触最紧的时候为0.2),由仿真车速对比可知,防滑控制提高了车辆在起伏路面行驶的车速,从而改善了车辆在障碍路面行驶的通过性。
5.4 部分车轮悬空仿真
该实验主要验证驱动力再分配控制对整车驱动力的影响效果。实验过程中,将车身固定,使第1、第3轴车轮悬空,第2、第4轴车轮着地,油门踏板开度为20%,仿真结果如图18所示。
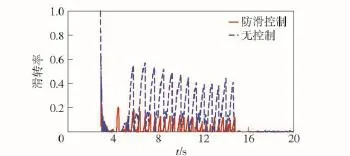
图16 车轮滑转率Fig.16 The wheel slip ratio
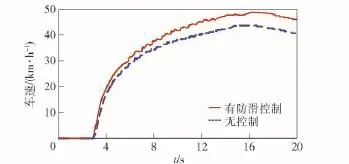
图17 车速曲线Fig.17 The curves of vehicle speed
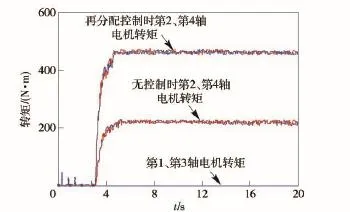
图18 电机输出转矩Fig.18 Motor torque output
驱动踏板给定各轴转矩约为220 N·m,由于第1、第3轴车轮悬空,在防滑控制器的作用下,其驱动电机转矩输出为0,无再分配控制时,整车牵引力将损失一半,而增加再分配控制后,第1、第3轴电机因悬空而减少的驱动力增加到第2、第4轴电机上,整车牵引力基本保持不变。
6 结论
针对多轮独立电驱动车辆,本文提出了一种层次化的驱动力优化控制结构,该结构包括基于各轴载荷的预分配、防滑控制和基于车辆状态的再分配控制3层控制。通过硬件在环实时仿真实验,验证了该分层控制方案能够实现驱动力在各驱动电机上的优化分配,改善了车辆的爬坡性能、直线加速性能以及障碍路面行驶的通过性,最大限度地发挥多轮独立电驱动车辆的性能优势。
References)
[1]Maeda K,Fujimoto H,Hori Y.Four-wheel driving-force distribution method for instantaneous or split slippery roads forelectric vehicle with in-wheel motors[C]//The 12th IEEE International Workshop on Advanced Motion Control.Sarajevo,Bosnia:IEEE,2012:1-6.
[2]Zhang L P,Li L,Qi B N,et al.Torque adaptive traction control for distributed drive electric vehicle[J].Journal of Mechanical Engineering,2013,20(13):106-113.
[3]Kawabe T.Model predictive PID traction control systems for electric vehicles[C]//2012 IEEE International Conference on Control Applications.Dubrovnik,Croatia:IEEE,2012:112-117.
[4]Ha H,Kim J,Lee J.VDC of in-wheel EV simulation based on precise wheel torque control[J].Lecture Notes in Computer Science,2013,8102:56-65.
[5]Hiraku O,Murakami,T.Improvement of vehicle stability by reaction force control on accelerator pedal and steering wheel[C]//International Power Electronics Conference.Sapporo,Japan:IEEE,2010:2956-2963.
[6]de Castro R,Araújo R E,Freitas D.Wheel slip control of EVsbased on sliding mode technique with conditional integrators[J].IEEE Transactions on Industrial Electronics,2013,60(8): 3256-3271.
[7]苏建强,马晓军,许世蒙,等.多轮电驱动装甲车辆车轮防滑控制[J].汽车工程,2014,36(5):592-596.SU Jian-qiang,MA Xiao-jun,XU Shi-meng,et al.Anti-slip control of armored vehicle with multi-in-wheel motors drive[J].Automotive Engineering,2014,36(5):592-596.(in Chinese)
[8]刘春明,张承宁,刘志福.8×8轮毂电机全轮驱动车辆动力学建模与仿真[J].北京理工大学学报,2014,34(2):143-147.LIU Chun-ming,ZHANG Cheng-ning,WANG Zhi-fu.Dynamics modeling and simulation on four-axle[J].Transactions of Beijing Institute of Technology,2014,34(2):143-147.(in Chinese)
A Study of Driving Force Optimal Control of Multi-wheel Independent Electric Drive Vehicle
YANG Gui-bing,LIAO Zi-li,MA Xiao-jun,LIU Chun-guang
(The Key Lab of All-electric Technology of Land Warfare Platform,Academy of Armored Force Engineering,Beijing 100072,China)
In order to improve the power performance of multi-wheel independent electric drive vehicle,a hierarchical control structure is established to realize the optimal control of the whole vehicle driving force.This kind of control structure includes an predistribution control of load on each axis,the acceleration slip regulation(ASR)and the redistribution based on state of vehicle.The ASR is the core layer which adopts a slip mode control method based on the road's optimal slip rate,and an abnormal fault detector based on cumulative sum(CUSUM)statistical control is designed.The optimal estimation of slip rate can be realized based on μ-λ figure.The hierarchical control structure can be used to achive the optimal distribution of drive force between axis and driving motor based on the output control of single wheel's optimal control.The control structure is proven by a real-time simulation in hardware in loop (HIL)in order to improve the vehicle's performances,including climbing ability,directly accelerating ability,and trafficability.
control science and technology;multi-wheel independent electric drive;power performance;acceleration slip regulation;optimal control
TJ81
A
1000-1093(2016)01-0023-08
2015-05-05
军队科研项目(40402050101)
阳贵兵(1987—),男,博士研究生。E-mail:ygb1987@163.com;廖自力(1974—),男,副教授,硕士生导师。E-mail:569024533@qq.com

