回路参数对霍尔推力器点火脉冲电流影响
杜建华,胡俊锋,杨子怡
1.北京控制工程研究所,北京100094 2.哈尔滨工业大学 先进动力研究所,哈尔滨 150001
回路参数对霍尔推力器点火脉冲电流影响
杜建华1,*,胡俊锋2,杨子怡2
1.北京控制工程研究所,北京100094 2.哈尔滨工业大学 先进动力研究所,哈尔滨 150001
在分析霍尔推力器点火启动过程中电源侧脉冲电流形成机理的基础上,通过解析分析和变参数试验的方法研究了外回路参数与电源侧脉冲电流峰值之间的规律。研究结果表明,随着外回路电容和电感的增大,电源脉冲点火电流峰值减小,根据理论推导得到的霍尔推力器点火启动过程电源脉冲电流峰值函数,分析了外回路电感、电容参数对点火脉冲电流的影响,给出了给定电感值下电感线圈匝数、磁环导磁截面积、磁芯材料BH曲线的要求,为霍尔推力器放电外回路的参数设计提供理论参考。
霍尔推力器;电源侧脉冲电流;点火启动;外回路参数;电感
霍尔推力器稳定工作的前提是确保其可靠点火,尤其在应用于小卫星编队飞行任务[1]或高精度脉宽调制模式时,推力器将频繁地经历点火与关机过程[2]。而在霍尔推力器点火过程中,电源侧会出现一个脉冲电流,脉冲电流持续时间约为几十微秒,脉冲电流峰值为正常电源回路电流数十倍,电源端脉冲电流峰值甚至会短时超过电源保护电流的整定值,严重影响霍尔推力器的安全运行。尽管霍尔推力器点火启动过程只有几十微秒,这几十微秒的特性对推力器系统影响很大,电流冲击可能会破坏推力器整体绝缘性,甚至会冲击整个电路的电源系统,严重影响推力器在轨运行的可靠性。因此,航天器在轨运行过程中,需要保证推力器的可靠点火,同时尽可能降低点火冲击。
霍尔推力器点火启动过程本质上是正交电磁场下的气体雪崩击穿过程,对于正交电磁场下气体击穿理论研究是有借鉴意义的。Meyer研究空气击穿电压在存在横向磁场条件下的变化,并在试验中发现最小击穿电压所对应的压力变化[3]。Wehrli通过计算,得到磁场对击穿条件和汤生系数的影响[4]。Blevin和Haydon着重考虑气体击穿时电子雪崩过程,初步得到磁场存在时,气体击穿过程中电子能量,漂移速度和汤生系数的变化[5-6]。Petraconi和Maciel研究磁场对电离系数和二次发射电子系数的影响,结果表明当外加与电场正交磁场时,气体击穿电压会降低[7]。Blevin和Brennan通过研究正交磁场下气体击穿过程中电子群位置以确定电离率、电子漂移速度等,进而分析磁场对汤生放电特性[8]。
霍尔推力器点火启动过程,是多参数相互耦合过程,其成功与否除了与放电电压、励磁电流和质量流量等宏观放电参数有关,还受到外回路参数的影响。法国的Vial和俄罗斯Arkhipov分别在试验中发现放电电流在推力器点火瞬间会有一个脉冲。不同的是,Arkhipov在推力器启动过程中观察到两个电流峰值,并认为第1个电流峰值与电源滤波器的电容放电有关,第2个脉冲电流是通道内大量氙原子电离所致。Vial在点火瞬间发现的电流峰值大约为正常放电电流的数倍,并且之后放电电流会出现与呼吸机制有关的低频振荡。Arkhipov还进行不同滤波器参数下的点火试验,建立发动机内部放电特性与外回路参数间的联系,得到电源电路参数决定脉冲电流持续时间的结论[9-10]。
普林斯顿大学的Ellison和Raitses通过高速CCD相机研究点火启动过程,展示了从推力器点火到稳定50 μs时间段内的电离过程[11]。同时,Vial利用高速CCD相机研究点火启动过程各表征参数随时间演化过程[10],结果显示等离子振荡与呼吸振荡模式有关,启动过程羽流区周期性的振荡是电离区从阴极逐渐向阳极移动的结果。
Taccogna建立了包括整个放电通道的二维轴对称模型,对霍尔推力器的点火过程进行模拟研究。同时,为了减小模拟计算量,Taccogna采用相似设计方法,通过PIC模拟得到了点火过程中电势、电子、离子和等离子体密度等参数随时间的变化过程[12]。哈尔滨工业大学的刘辉考虑到点火启动过程中的特殊性,把电子看作一个能够发射20 A电子电流的热阴极,对Taccogna原有模型进行修正,同时在模型中考虑了推力器的近场羽流区。因此,模拟结果与实际测量结果相似,再现了点火过程放电电流峰值的演化过程[13]。
本文将从电源侧脉冲电流形成的物理机理出发,通过试验的方法研究电源侧脉冲电流变化规律,然后从发动机内部放电特性和外回路滤波单元两个层面分析电源侧脉冲电流的影响机理,进而推导得到电源脉冲电流峰值的理论公式,给出电源电流峰值合理的预测边界。
1 试验系统
试验平台主要包括真空系统,发动机系统,控制与测量系统。实验室的真空系统包括真空罐、抽真空设备、测量真空的真空计、控制阀门和连接管路。真空罐直径为1.2 m,长4 m,由无磁性不锈钢组成,其静态真空度能达到10-3Pa量级,满足试验要求真空度。
试验中使用的霍尔推力器是HPPL研制的千瓦级HET-100试验样机。霍尔推力器放电通道是由氮化硼陶瓷加工而成,外陶瓷套筒直径为100 mm,通道轴向尺寸为51 mm。HET-100所使用的工作介质为纯度为99.999%的氙气。额定工况下,分别利用100 mL/min和10 mL/min的两个AFC50D质量流量计为推力器和阴极供气,流量计的控制精度小于1%,直流稳压电源单独为推力器和串联励磁线圈供电。
试验测量装置采用Yokogawa公司横河DL850示波记录仪。垂直分辨率12 bit,可实现最大1 000 V输入,条件动作触发等功能。
试验中点火电路如图1所示,外回路参数对电源端电流影响实验的设计流程如下:

图1 供电系统示意Fig.1 Power supply schematic diagram
1)启动系统,确保真空罐的真空条件,保持HET-100最优工况下的放电参数不变:采用氙气工质,工质阳极流量42.8 mL/min,放电电压260 V,采用同一串联励磁电流,励磁电流3.5 A。
2)在放电参数不变的条件下,开始进行外回路参数改变的点火试验。首先,保证滤波单元的电感不变,电容从10 μF开始,以步距10 μF逐渐增加到70 μF,每一电容值下进行点火10次,测量HET-100启动过程中电源端脉冲电流变化情况。然后,在同一试验条件下,电容固定为10 μF和30 μF,改变电感值范围0.1~0.7 mH@0.1 mH/step,不同电感值下推力器进行10次点火,测量推力器启动过程中电源端脉冲电流特性。
2 试验结果及讨论
现有的研究表明,霍尔推力器点火启动过程中,电源端不可避免地会出现一个持续时间大约为几十微秒,峰值大约为几百安培的脉冲电流。众所周知,出于安全性,通常电源会设定一个过流保护值,一旦电流超过过流值,电源就会自动关闭输出[14]。因此,点火启动过程中,这种电源电流峰值的不确定性导致电源过流值设定存在不确定性,影响推力器的可靠运行。同时,在任一能满足推力器成功点火的放电参数下,点火启动过程中电源电流峰值都是推力器稳定运行时电源电流的数十倍,瞬间高电流会冲击电源系统,引起电磁干扰,影响电源使用寿命[15]。
点火瞬间放电脉冲电流是通道内原子瞬间雪崩式电离的结果。瞬间高电流造成由电阻、电容和电感三者组成的滤波电路中电容两端电压下降,电容两端电压跌落,电源会通过电感与电阻给电容充电,导致发动机电源端形成脉冲电流。点火启动过程时间数量级为微秒量级,时间很短,所以根据点火电路及基尔霍夫定律,点火启动过程中电源端电流可以表示为
(1)
式中:IP为电源端电流;Id0为推力器稳定工作时的放电电流;C为电容器电容;ΔU为电容两端的电压降;Δt为电容充电时间。
大量的试验结果表明,当电源电流达到最大值时,放电电流已基本趋于稳定,因此式(1)中Id0表示推力器稳定运行时的放电电流,并可以初步认为电源电流峰值主要取决于电容两端的电压降以及电容充电时间。电容器充电时间与RLC滤波电路参数有关,由电路理论基础和角频率可以计算谐振周期
(2)
式中:T为谐振周期;L为滤波单元电感。
根据试验结果可得电容充电时间大约为其固有周期的1/4,即电源端电流表达式可表示为
(3)
利用电路理论及电感定义式,并结合以上各式可以得到
(4)
式中:μ为磁导率;N为电感线圈匝数;S为电感磁路的横截面积;li为电感磁路长度。
如果流过电感的电流没有超过允许值范围,电感的电感值不会改变,如果电感上电流过大,磁导率μ将会减小,电感值L也会随之减小。更确切地说,根据磁化曲线,B与H之间存在一段非线性关系饱和区域,该区域内,当H增加时,B几乎不怎么改变。这主要是由于电流引起电感L变化引起的,变化关系体现在磁导率的不同。因此,用指数函数形式对磁导率μ和磁场强度H之间的关系进行拟合,拟合函数
(5)
式中:a,b为拟合系数;μ0为真空磁导率;H为磁场强度。综合电路理论和式(5)可得
(6)
将式(6)带入式(4),可以得到推力器点火启动过程中电感的变化关系式:
(7)
在推力器点火启动过程中,电感会出现磁饱和现象,电感值瞬间减小。此时电感的阻抗只有几欧,然而,试验中与电感并联的电阻阻值为120 Ω,远大于电感的阻抗值。因此,可以忽略通过电阻的电流,认为电流只通过电感给电容充电。将L表达式(7)带入式(3)中,同时Id0考虑到远小于Ip,因此,式(3)可以表示为:
(8)
从电源电流峰值公式(8)中不难看出,电源电流峰值取决于外回路电感参数和电容两端电压降,而电容两端电压降与电容、推力器阳极流量,放电电压等放电参数有关,即电源电流峰值不仅受放电参数的影响,同时也受外回路参数的影响。
2.1电容对电源侧脉冲电流的影响
试验分别测量了不同电容下推力器点火启动过程中电源端脉冲电流,统计结果得到电源端脉冲电流峰值随电容变化规律,如图2所示。从图中可以看出,推力器点火启动过程中电源端脉冲电流峰值随电容增大逐渐减小。根据上节中对电源端电流形成机理分析,由式(8)可知,在其他参数不变的前提下,当电容值增加时,电源端电流脉冲峰值将随之增加,而试验结果却出现与公式相反结果,这意味着电容值的改变同时还伴随着其他参数的变化。

图2 电源脉冲电流和电容两端电压降随电容变化规律Fig.2 Variation of the power pulse current andthe voltage drop across capacitance with capacitances
为分析具体参数变化,结合电容本身特性进行分析,电容值大小表征电容储存电荷能力,即电容维持其两端电压的能力。电容值C越大,电容储存电荷能力越强,电容两端电压变化越小。因此,电容值的改变会引起推力器点火启动过程中电容两端电压降的变化。图2同时给出了推力器点火启动过程中电容两端电压降随电容变化情况。可见,电容两端电压降在电容增加情况下有明显减小趋势。
综合考虑,当外回路电容参数变化时,Ipmax公式中会出现电容C和电容电压降ΔU的变化,并且两者变化方向相反。比较来看,ΔU的变化范围远大于C的变化范围,C对电流峰值的影响在微安数量级,而ΔU对电流峰值的影响在几十安数量级上,因此,在探讨电容对电源端脉冲电流峰值影响时,忽略电容值本身的变化,主要考虑电容改变引起电容两端电压降的变化,从而导致电源端脉冲电流峰值的变化。其变化规律表现为:随着滤波器电容的增加,推力器点火启动过程电源端脉冲电流峰值是减小的。经过分析外回路参数的影响机理,改变滤波器参数得到电源脉冲电流峰值理想的减小趋势,这对减小电源电流冲击,未来解决推力器电源安全可靠性具有借鉴意义。
2.2电感对电源侧脉冲电流的影响
(1)电感量对电源侧脉冲电流的影响
根据所述试验方案进行电感点火试验,对点火启动过程电源端脉冲电流峰值进行统计,得到推力器点火启动过程,电源端脉冲电流峰值与电感的关系如图3所示。

图3 电源脉冲电流随电感变化规律Fig.3 Relationship between power pulse current and inductances
从图3中可以看出,在不同的电容下,推力器点火启动过程中,电源端电流峰值随着电感值的增加而减小。根据电源电流峰值式(8)可知,电源电流峰值与电感有关,试验中电感参数变化主要是通过改变电感线圈匝数和电感磁路,于是式(8)中会有两个变化量,较难得出Ip与电感的变化趋势。由L与电源电流峰值Ip之间的关系式(3)可知,Ip反比于L,即随着L的增加,Ip减小。针对L与Ip反比关系的可能性解释如下:由电感在电路中的作用可知,电感主要作用是阻碍电流变化,电感值越大,电感阻碍电流变化作用越强,即推力器滤波电路中电流变化趋势变缓,电源电流峰值变小,因此,电源电流峰值随着电感值增加具有减小趋势。简单来看,电源电流峰值随电感增加而减小这一试验结果与理论分析趋势定性吻合。
(2)不同电感参数下的电源脉冲电流峰值理论预测边界
推力器点火启动过程中,不同放电参数下电源脉冲电流峰值的试验研究表明,电源脉冲电流峰值最终取决于推力器点火启动过程中放电通道内原子电离电荷量。启动过程中的极限情况是通道内所有原子全部被电离。因此,可以利用原子全部电离的电荷数来估算点火启动过程中电源脉冲电流峰值的最大值。假设推力器点火启动过程中,放电通道内氙原子为理想气体,并且在此过程中全部被电离。根据理想气体的状态方程,可得发动机点火启动过程中,原子电离电荷量
(9)
式中:e=1.6×10-9C,为电子电荷;N为原子总数量;P(l)为点火前通道内压力;R为理想气体常数;T为点火前氙原子温度;NA=6.02×1023为阿伏伽德罗常数;SC为放电通道横截面积;l1为气体分配器对应的轴向坐标,规定l1=0;l2为放电通道出口对应的轴向坐标。
针对本试验中HET-100型号推力器,有R=8.3J/(molK),T=300K,SC=4.0×10-3m2,l1=0,l2=50mm。
整理得到推力器点火启动过程中电源脉冲电流峰值最大值
(10)
由电源脉冲电流峰值理论预测公式(10)可以看出,当放电参数确定后,放电通道内原子数目就已确定,即相同工况下滤波器参数是影响电源脉冲电流峰值的主要因素,对于匹配的滤波器参数,则滤波器中各元件的选择至关重要。
式(10)中显示电感参数的选择最为重要,比如,同为0.1mH的电感,电感输入参数的改变将直接反映在式(10)中,磁芯的改变会改变公式中拟合参数a和b,线圈匝数N,磁环导磁截面积S以及磁路的长度li都是式(10)的主要参数[16],因此在匹配滤波器参数L=0.1mH,C=10μF和R=120不变的条件下,改变电感相关输入参数。首先在磁芯材料以及电感值L不变的前提下,分别改变线圈匝数、磁环导磁截面积和磁环回路长度,变化参数如表1所示,根据电感输入参数利用式(10)得到不同参数下推力器点火启动过程中电源脉冲电流峰值,如图4所示。

表1 电感参数变化
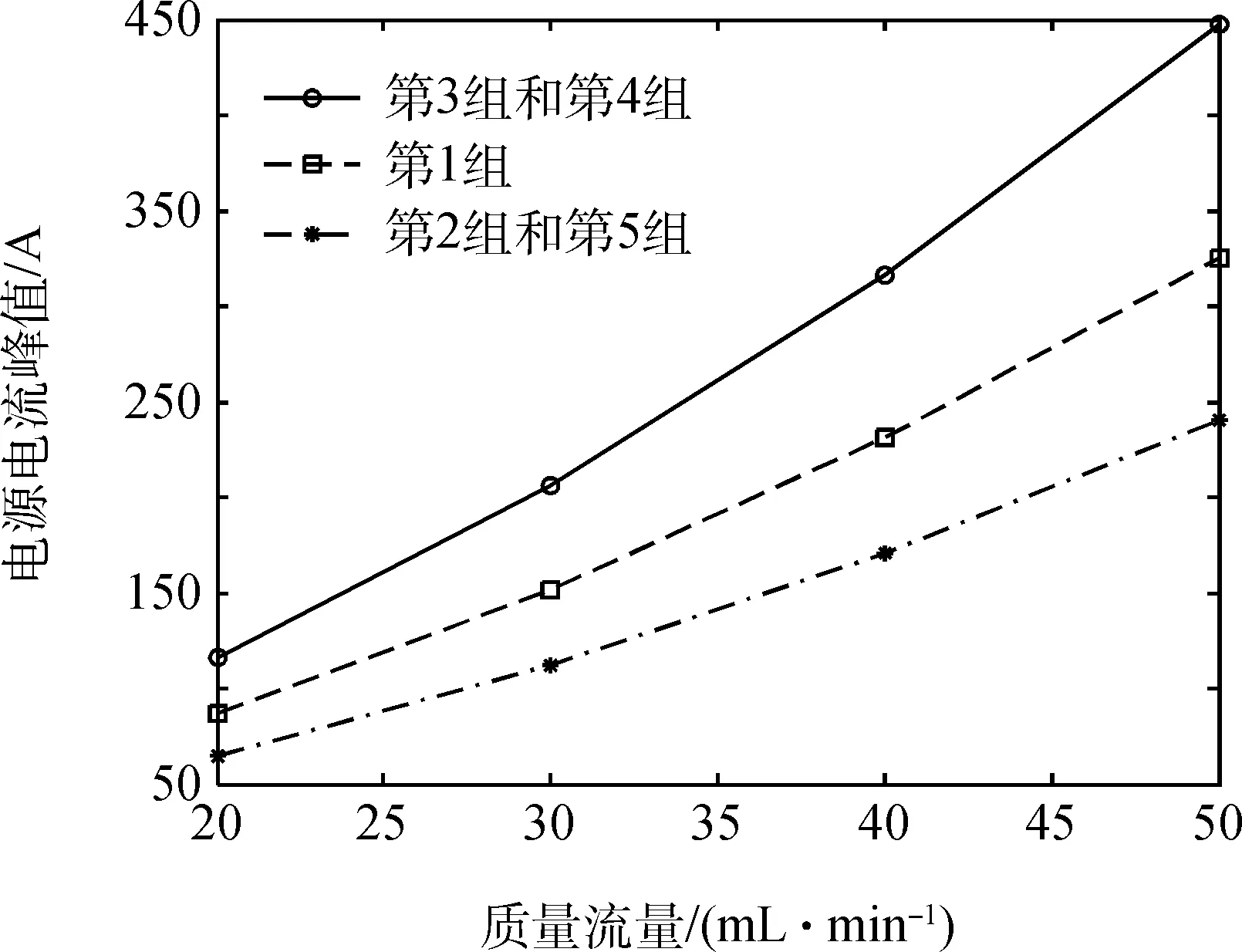
图4 不同电感参数下的电源侧脉冲电流Fig.4 Power pulse current under different inductance parameters
结果中显示,在相同滤波器参数条件下,推力器点火启动过程中,电源脉冲电流峰值与制作电感的线圈匝数与磁环导磁截面积乘积有关,只要保证两者乘积不变,通过式(10)计算所得的电源电流峰值的预测值就不变,见图4中最上面一条线和最下面一条线,N、S和li不同,但是制作电感的线圈匝数与磁环导磁截面积乘积相同,两者预测值相同。
同时,从图4中可以看出,在相同滤波器参数下,霍尔推力器在启动过程中的电源脉冲电流峰值的预测值会随着电感的线圈匝数与磁环导磁截面积乘积减小而增加。此结果对滤波器的选择具有指导意义,在确定滤波器参数条件下,在选择相同参数的电感下,应该选择线圈匝数与环磁导磁截面积乘积较大的电感,即相同电感值下,线圈匝数较多,导磁环较大的电感更有利于减小霍尔推力器点火启动过程中电源脉冲电流的峰值。
随后,保证式(10)中N、S和li不变,改变公式中a和b的值,也即是不改变电感值的条件下改变磁芯材料。因此,本文选取了5种不同磁芯材料进行对应的5组试验,图5反映了不同磁芯材料的电感磁导率随着磁场强度的变化规律,可以看出,5种磁芯材料电感磁导率均随着磁场强度增大而减小,其中材料5的电感磁导率随磁场强度变化最慢。
根据式(10)对电源侧电流峰值进行预测,预测结果如图6所示。从试验结果来看,在相同工况下第4组试验电源侧脉冲电流峰值明显高于其他4组对应的值,相反的是,第5组的电源侧脉冲电流峰值最小。结合图5,可以根据此变化趋势初步判断,制作电感的电感磁芯应该选择磁芯饱和时B随H变化慢的材料。

图5 不同材料的电感磁导率随磁场强度变化规律Fig.5 Inductance permeability of different materials as a function of magnetic field intensity
电感磁芯材料。线圈匝数、横截面积和有效长度的分析模拟结果揭示了推力器滤波单元中电感参数的选择原则,将霍尔推力器在启动过程中的电源脉冲电流峰值的预测值最小化,这为霍尔推力器电源设计、过流保护整定提供了强有力地依据。

图6 不同磁性材料下电源侧脉冲电流Fig.6 Power pulse current under different magnetic materials
3 结束语
本文首先理论分析了推力器点火启动过程中,电源端脉冲电流形成机理。并通过解析分析和试验的方法主要研究了滤波器参数对电源脉冲电流峰值的影响。结果表明,当滤波器电容参数增加,电感参数增加时,电源脉冲电流峰值具有理想的减小趋势。这些规律在一定程度上指出了减小电源电流冲击的措施。最后,根据试验结果,提出一种确定霍尔推力器启动过程电源脉冲电流峰值最大值的方法,在霍尔推力器不点火的前提下,给定不同质量流量下电源脉冲电流理论预测最大值,并推导得到电源脉冲电流峰值函数,为确保霍尔推力器安全点火提供理论依据。
其中,根据电源脉冲电流峰值理论预测公式,进一步研究了不同电感参数下电流峰值的理论预测边界。试验结果表明:一方面,在相同滤波器参数下,霍尔推力器在启动过程中的电源脉冲电流峰值的预测值会随着作电感的线圈匝数与磁环导磁截面积乘积减小而增加。也即是在相同电感值时,线圈匝数较多,导磁环较大的电感更有利于减小霍尔推力器点火启动过程中电源脉冲电流的峰值。另一方面,磁芯饱和值越大,磁芯饱和时变化趋势越小,其所对应的电源脉冲电流峰值越小。与此,根据此变化趋势初步判断,制作电感的电感磁芯应该选择即磁芯饱和时B随H变化慢的材料。
References)
[1]谢红军,洪鑫. 深空探测器推进系统[J]. 上海航天,2003,20(2):38-43.
XIE H J, HONG X. The propulsion system of deep space detector[J]. Aerospace Shanghai,2003, 20(2):38-43(in Chinese).
[2]HOSKINS W A, CASSADY R J. 30 years of electric propulsion flight experience at aerojet rocketdyne[C] ∥33rd International Electric Propulsion Conference.Washington D.C.,2013:1-10.
[3]MEYER BOICHENKO A , TKACHEV A N. Boundary between the regions of drift and runaway of electrons outside the townsend discharge domain boundary[J]. Technical Physics, 2014, 59(9): 1334-1337.
[4]WEHRLI M. Funkenpotentiale im transversalen magnetfelde[J]. Annalen der Physik, 1922, 374(20): 285-314.
[5]BLEVIN H A, HAYDON S C. The townsend ionization coefficients in crossed electric and magnetic fields[J]. Australian Journal of Physics, 1958, 11(1): 18-34.
[6]BLEVIN H A, HAYDON S C. The interpretation of breakdown characteristics of electrodeless discharges in transverse magnetic fields[J]. Proceedings of the Physical Society, 1963, 81(3): 490.
[7]PETRACONI G, MACIEL H S, PESSOA R S, et al. Longitudinal magnetic field effect on the electrical breakdown in low pressure gases[J]. Brazilian Journal of Physics, 2004, 34(4B): 1662-1666.
[8]BLEVIN H A, BRENNAN M J. Townsend discharges in transverse magnetic fields[J]. Australian Journal of Physics, 1983, 36(6): 859-866.
[9]ARKHIPON ZHAKUPOV A, KHARTOV S, LATYSHEV L. Hall thruster with a sectioned conducting channel[J].Spacecraft Propulsion, 2000,465:827.
[10]VIAL V, MAZOUFFRE S, PRIOUL M, et al. CCD images of Hall effect thruster plume dynamics after ultrafast current ignition[J]. IEEE Transactions on Plasma Science, 2005, 33(2): 524-525.
[11]ELLISON C L, RAITSES Y, FISCH N J. Fast camera imaging of Hall thruster ignition[J]. IEEE Transactions on Plasma Science, 2011, 39(11): 2950.
[12]TACCOGNA F, LONGO S, CAPITELLI M, et al. Start-up transient in a Hall Thruster[J]. Contributions to Plasma Physics, 2006, 46(10): 781-786.
[13]LIU H, YU D R, YAN G J, et al. Investigation of the start transient in a Hall thruster[J]. Contributions to Plasma Physics, 2008, 48(9-10): 603-611.
[14]杨乐. 脉冲等离子体推力器工作过程理论和实验研究[D]. 合肥:国防科学技术大学, 2007:86-90.
YANG L. Theoretical and experimental study of pulsed plasma thruster operation process[D]. Hefei:National University of Defense Technology, 2007:86-90(in Chinese).
[15]李林凌, 刘伟, 赵烁. 电推进系统空间试验技术研究[J]. 航天器工程, 2014, 23(3): 126-132.
LI L L, LIU W, ZHAO S. Study on sapce test of electric propulsion system[J]. Spacecraft Engineering, 2014, 23(3):126-132(in Chinese).
[16]HOGAS M, RYDLER K E, STENARSON J, et al. Analytic solution of the magnetic field and inductance in a coaxial short circuit[J]. IEEE Transactions on Instrumentation and Measurement,2015,(6):1582-1587.
(编辑:高珍)
Effect of circuit parameters on start-up transient current of Hall thrusters
DU Jianhua1,*,HU Junfeng2,YANG Ziyi2
1. Beijing Institute of Control Engineering, Beijing 100094, China 2. Institute of Advanced Power,Harbin Institute of Technology, Harbin 150001, China
Based on the analysis of the formation mechanism of the pulse current in the power supply side during the start-up transient, the relationship between the outer circuit parameters and the pulse current peek in the power supply side was studied by the analysis and experiments under varying parameters. Results show that the pulse current on the power supply side decreases with the increase of capacitance and inductance. Based on the deduced function of peak pulse current on the power supply side, the effects of capacitance and inductance on the power supply pulse current during a Hall thruster start-up transient was studied. The requirement of the turn, magnetic core sectional area, and the BH curve of selected inductor was discussed.This research can provide reference for the outer circuit parameter design in Hall thrusters.
Hall thruster;pulse current in the power supply side; start-up process; outer circuit parameters; inductance
10.16708/j.cnki.1000-758X.2016.0045
2015-11-26;
2015-12-30;录用日期:2016-05-11;
时间:2016-07-1213:26:39
http:∥www.cnki.net/kcms/detail/11.1859.V.20160712.1326.003.html
国家自然科学基金(51477035)
杜建华(1979-),男,高级工程师,wonderful0579@126.com,主要研究方向为空间数字电源、电推进电源
V430
A
http:∥zgkj.cast.cn
引用格式:杜建华,胡俊锋,杨子怡.回路参数对霍尔推力器点火脉冲电流影响[J].中国空间科学技术, 2016,36(4):
51-57.DUJH,HUJF,YANGZY.Effectofcircuitparametersonstart-uptransientcurrentofHallthrusters[J].ChineseSpaceScienceandTechnology, 2016,36:(4)51-57(inChinese).

