钢构企业生产调度系统的研究与应用
花季伟 佟静翠 雷兆明
1(天津师范大学计算机与信息工程学院 天津 300387)2(河北工业大学控制科学与工程学院 天津 300401)
钢构企业生产调度系统的研究与应用
花季伟1佟静翠2雷兆明2
1(天津师范大学计算机与信息工程学院天津 300387)2(河北工业大学控制科学与工程学院天津 300401)
一个好的生产调度系统可以给钢结构企业的生产带来巨大的收益,但钢构企业的生产调度约束复杂、寻优困难。针对该调度问题提出基于蚁群遗传混合算法的生产调度模型,并解决动态调度情况下的紧急工件插入问题。以河北省某钢结构企业为依托,对该生产调度系统执行情况进行研究,实验结果表明,该蚁群遗传混合算法在钢构企业生产调度中的应用可以提高生产效率。
钢结构生产调度蚁群遗传混合算法动态调度
0 引 言
在信息化飞速发展的今天,企业越来越开始关注合理而高效的生产管理系统。这是因为合理而高效的生产管理系统可以保障企业的生产调度合理顺畅的实施[1]。由于钢结构产品具有强度高、塑性和韧性好,材质均匀等特点,因此在人们的生产生活中得到了广泛使用,随之而来的就是钢结构企业的迅速发展。这就需要钢结构企业在进行生产时配以行之有效的生产调度系统,从而达到提高生产效率,减少劳力和机械损耗等的目的。本文以某钢构企业实际生产调度为基础,以提高企业利润、优化生产方案为目标,研究基于蚁群遗传的混合算法的生产调度系统。
Job-Shop调度是许多学科研究的热点,同时也是典型的NP难题[2]。非人工智能的调度方法有基于运筹学的方法、启发式调度方法、基于仿真的方法,这些方法都对实际情况进行了理想处理,使计划与生产调度脱节,结果难以实用化[3]。人工智能调度方法是基于人工智能技术和人类调度专家经验对调度问题进行建模并求解的方法总称。目前国内已有很多该方面的研究,王海瑶[4]等建立基于双层规则组合的Job Shop多目标柔性调度方法;姜桦[5]等以旅行商问题说明了蚁群算法的模型结构。本文结合钢结构的实际生产,建立了多目标生产数学模型,较好地解决了钢构企业的生产调度难题。
1 功能简介
对钢结构企业而言,生产管理系统面临的最大困难是如何面向多构件生产进行有效的组织生产。钢构件在生产过程中会受到众多条件因素的影响,如不同品种、构件的工序数、工序的班组分配、紧急件的动态插入等,所以设计一个高效的生产调度系统是企业生产环节的关键所在。
生产调度是将产品的生产顺序解析成为设备、原料等生产资源的分配顺序,以客户的订单需求为目标,结合企业的生产能力和其他各方面的实际约束,对生产资源进行合理分配,以达到提高生产效率、增加企业利润的目标,从而指导企业生产的各个环节有序进行。所以生产计划与生产调度系统的功能模块如图1所示。

图1 生产计划与调度系统图
以下是对生产计划与调度系统中主要模块的简介:1) 工序拆分模块负责将要生产的钢构件进行拆分,生成不同的生产工序,以便班组对其进行加工;2) 生产计划模块负责将同一批次的钢构件工序进行排产,生成工序的生产时间及负责生产的班组,该模块的工序的排产方案由本文提出的混合算法来实现;3) 计划进度模块,各班组负责人可以通过查询该模块来了解各自班组的近期生产计划;4) 计划调整模块,当有紧急钢构件需要加工处理时,可以通过计划调整模块来实现对现有生产计划的调整,也就是动态调度的过程。
2 算法分析
钢结构企业生产属于柔性、离散的生产过程,问题主要有:1) 工序多班组选择问题;2) 动态调度问题。工序在加工时如果选择加工班组不当或加工时间安排不合理就会使生产效率下降,导致企业利润受损。当有紧急件需要处理时,如果安排不当不仅会影响紧急件的完工时间,甚至会导致其他构件不能按时完成。所以需要一个合理的算法来制定高效的生产计划。针对以上情况本文采用分层法解决柔性调度问题。根据生产系统开发目标构建数学模型,首先利用蚁群算法避免大量冗余迭代的特点解决班组选择问题。然后借鉴遗传算法的良好的全局搜索性优势解决作业调度问题,以使生产系统相关性能指标最优。如总完工时间,生产能力与负荷均衡;而对于动态调度问题主要是解决紧急件插入情况,具体解决办法根据紧急构件插入时间点而定。
2.1问题描述
钢构件工序的多班组选择的问题描述:n个构件在g个不同班组上加工,每个构件x道工序(x>1),提前给出各构件的工序加工顺序。每道工序可以在若干个班组上加工,且不同的班组加工同一道工序所用的工时不同。该生产调度的目标是为每个钢构件的每道工序找到合适的班组,并确定每个班组上的工序加工顺序及加工时间,使各个班组的生产能力与负荷均衡且完成总任务时间最短这一性能指标最优。
针对问题描述可对生产过程做出以下约束:
1) 工序在加工过程中不能中断;
2) 同一种钢构件的各工序间具有加工顺序,不同钢构件间的工序加工不具有加工顺序;
3) 预先给定了工序在班组上的加工时长;
4) 同一时刻一个钢构件只能在一个班组上加工,且班组不能同时加工多道工序。
以下是对数学模型中参数和变量进行的说明:
g:加工班组总数
n:钢构件总数
i,j:钢构件序号,i,j=1,2,…,n
k:设备序号,k=1,2,…,m
Tj:第j个钢构件的工序总数
Ojx:第j个钢构件第x道工序
Mkjx:第j个钢构件第x道工序在班组i上加工
tkjx:第j个钢构件第x道工序在班组i上加工时间
bjx:第j个钢构件第x道工序加工开始时间
fjx:第j个钢构件第x道工序加工结束时间
CMax:最大的完工时间
该问题的约束条件如下:
1) 同一个钢构件的加工工序优先级不同,如式(1)和式(2):
bjx+(Mkjx×tkjx)≤fjx
(1)
fjx≤bj(x+1)
(2)
2) 同一时刻,班组k不能同时加工不同的钢构件,如式(3):
bkjx+ tkjx≤bki l×rkjxil
(3)
钢构件j的第x道工序在班组k上加工时Mkjx为1,否则Mkjx为0。
钢构件j的第x道工序在班组k上加工且钢构件i的第l道工序在班组k上加工时rkjxil为1,否则rkjxil为0 。
多目标优化数学模型:
已知决策向量X=(x1,x2,…,xz),约束条件为:
Gp(x)≥0(p=1,2,…,l)
(4)
Hq(X)=0(q=1,2,…,z)
(5)
设相互冲突的优化目标有n个,则优化目标为:
F(X)=(F1(X), F2(X),…,Fn(X))
(6)
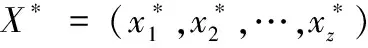
根据上述约束条件,可以对模型中的钢构件进行调度,以此来确定生产调度的最优解。考虑到生产调度中会有多个目标函数的情况,所以有如下模型:
1) 瓶颈班组的负荷最小:
MinF1= Min(WM)= Min(Max(Wk))
(7)
其中,Wk表示班组k的负荷。
2) 班组的总负荷最小:
(8)
其中,Wk表示班组k负荷。
3) 所有钢构件完工时间最小:
MinF3= Min(Max(Cj))
(9)
其中,Cj表示钢构件j的最终完工时间。
所以Min(F1,F2,F3)即为多目标调度问题的数学模型。
2.2钢构件的多班组调度
本设计采用蚁群算法来获得多班组资源优化分配可行解,并将其作为班组约束,然后用遗传算法求解JSP问题。假设柔性作业调度模型参与的钢构件集{J1,J2,…,Jn},钢构件工序加工的班组集{ M1,M2,…,Mm}以及相应的时间集{T1,T2,…,Tt}。然后通过蚁群算法生成班组分配方案,再通过遗传算法对各班组进行优化,形成最终的排序方案,即最优调度结果。本文采用的是蚁群—遗传的开放式混合算法,即先用蚁群算法求出班组的最优分配方案,再用遗传算法求出各车间的工序排产方案,最终得到优化结果。
2.3已知工序的析取图模型
本文采用蚁群算法对FJSP的工艺路线问题进行求解,可将其看成是旅行商问题。将钢构件工序可选加工班组看成是城市的结点,然后将其表示成解构造图模型,有向弧代表当前工序加工完后可移向的班组方向。蚂蚁的解构造图为G=(V,CUD,τ) ( V表示所有节点的集合;C表示有向图G中所有有向弧的集合;D表示有向图G中所有析取边的集合;τ表示信息素分布,与解构造图上的弧相关联)。现以钢构件在车间6个班组的生产情况为例,6个班组分别为下料、组立、铆对、焊接、除锈和喷漆班组,分别用M1、M2、M3、M4、M5、M6表示。已知钢构件数、工序数及相应的加工工时,则析取图模型如表1所示。

表1 析取图模型
2.4班组分配规则
为了能够提高解的质量和缩短搜索时间,提升效率,本文所采取的策略是优先选中加工时长最短的班组。同时累计每个班组已负载的加工时间, 从而平衡各班组的工作负荷。设班组已负载的加工时间累计为CMsum(1×6矩阵),该矩阵初始化为[0,0,0,0,0,0],用于分别累计六个班组加工的工时。如当加工钢构件 J1的工序O11时,需选取加工时长最短班组M1,所以将该工时2加到矩阵CMsum的第一列中。
η为局部启发式信息,它的作用是指引蚂蚁选择加工时间最短的班组[7]。η的取值:ηij=1/(CM(1+CMsum)),CM表示选择M班组时的当前负载。则转移规则公式为:
(10)
2.5各班组中工序的优化
由上述的蚁群算法可得班组的最优分配方案,即确定出各钢构件工序的优选加工班组。这样就可以将工序多班组选择问题简化成钢构件工序在确定班组上的加工顺序及时间问题。也就是说该最优方案可作为设备约束条件,用于遗传算法的约束,进而通过遗传算法解决各车间的工序排产问题,并最终得到柔性作业车间调度的最优解。
综合考虑上述的约束条件,遗传算法可以采用以下的编码方式:每个染色体上的每一个基因代表工件的一道工序,该工序的加工班组已确定,染色体的长度为钢构件数与工序数的乘积[8]。
1) 编码:假设由蚁群算法求得的设备分配最优解为:J1的三道工序选择的班组分别为M1、M4、M1,J2的三道工序选择的班组分别为M5、M1、M3,以及J3J4的班组分配情况。随机生成的染色体[1 2 2 1 2 1 3 3 3 4 4 4],1表示钢构件J1,2表示钢构件J2,其中出现的三个1表示J1的三道工序,三个1在染色体中出现的位置表示三道工序的先后顺序,同理工件J2J3J4也是如此。
2) 适应度函数选择:由生产调度的模型约束知本文遗传算法的目标函数就是求钢构件最大完工时间最小,即式(9)。遗传算法的适应度函数:
(11)
其中F3是钢构件的完工时间,cmax根据钢构件加工时间经验而定,为常数。
3) 遗传算子操作:可采用轮盘赌的方式随机选取两条染色体,采用单点的方式进行交叉。对选的两条染色体依次从头增加向量长度,当两个向量含有相同的数字类别和长度时,便将该点作为交叉点进行交叉,保留最优个体。操作如下:

根据前面染色体定义的规则对染色体进行初始化,随机生成预知数量的染色体。规定迭代次数,再通过遗传算法的适应度计算、基于POX交叉策略的设计、采用逆序变异规则进行变异,对其进行算法迭代,最终得到算法的最优解。该最优解即为钢构件生产的最佳生产进度。
2.6动态调度问题的解决
车间生产过程是一个动态的调度过程,因此还需要在设计的基本调度方案(计划进度模块)上考虑紧急件插入的情况,对计划进度进行调整,即动态调度的情况。根据紧急件插入的时间点不同,分为四种情况:1) 在工序加工之前插入;2) 在工序加工过程中插入;3) 在工序间插入;4) 在所有工序完成后插入。针对不同情况解决方案如下:
1) 若紧急工序的所需时长<(工序开始时间-插入紧急工序时间点),则对整体调度无影响;否则,调度方案时间点右移(插入紧急工序时间点+插入紧急工序的所需时长-工序开始时间)。
2) 紧急工件紧接着其工序完成时间开始加工,若(下道工序开始时间-工序结束时间)>插入紧急工序的时长,则对整体调度无影响;否则,该工序后的所有工序后移(插入紧急工序的所需时长+工序结束时间-下道工序开始时间)。
3) 若插入紧急工序的时长<(下道工序开始时间-插入紧急工序时间点), 则对整体调度无影响;否则,调度方案时间点右移(插入紧急工序时间点+插入紧急工序的所需时长-下道工序开始时间)。
4) 若除当前设备外,在插入紧急工件时间点以后无工件工序处于加工或准备加工状态,则对整体调度无影响;否则,若其他设备处于加工状态,转2)处理;若其他设备处于准备加工状态,转3)处理。
通过对紧急件的处理,对计划进度进行调整,生成调整后的进度。通过计划进度模块与计划调整模块相结合即可确保各钢构件按时完成。
3 算法实现
本文采用的是开放式蚁群—遗传混合算法对作业调度问题求解。首先采用蚁群算法求解工序班组的优选问题,目的是确定待加工钢构件和该钢构件相关工序的优选班组;再采用遗传算法求解班组中的各道工序加工顺序和加工的起止时间。基本的参数设置如下:蚁群算法,蚂蚁数m、迭代数Nc、信息重要程度α、启发式因子重要程度β、信息素挥发系数ρ、信息素增强系数Q见表2所示;遗传算法,迭代次数maxGen、种群大小pop、交叉因子crossover、变异因子mutation、选择算子psel见表3所示。其工作流程如图2、图3所示。当考虑到紧急件插入情况时,其动态调度流程如图4所示。

表2 蚁群算法参数

表3 遗传算法参数

图2 遗传算法流程图
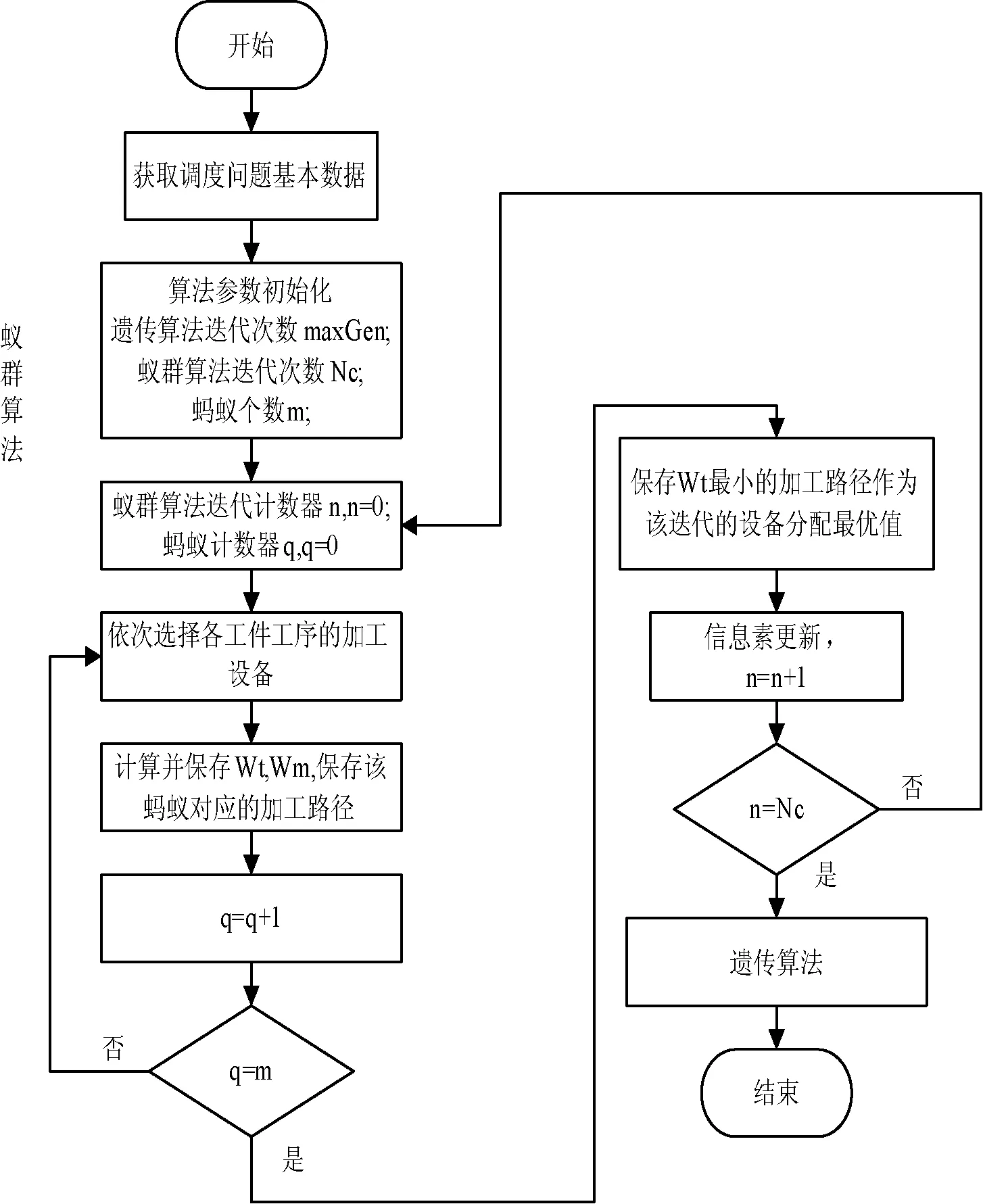
图3 蚁群遗传算法流程图

图4 动态调度流程图
4 实验及结果分析
已知该钢结构企业某车间共有6个班组,以表1给出的生产信息为例,对其进行仿真(算法参数参见表2和表3),并将其仿真结果与蚁群算法的仿真结果进行对比。表4给出了四种构件各自的加工总时间、生产的总时间及成功的次数。图5给出了结果仿真图,横坐标表示算法求解时迭代的次数,纵坐标表示加工所需的总工时(以天计算)。

表4 生产调度结果表

图5 两种算法仿真结果图
由仿真结果可以看出,在车间班组、工件数量、工序等相同的情况下,虽然两种算法最终收敛到的值差不多,但是蚁群遗传混合算法收敛速度明显优于蚁群算法的收敛速度,成功次数更高,故可靠性更好。可见该算法在一定程度上既节省了排产时间,又提高了生产效率。
5 结 语
本文首先对生产计划与生产调度系统的主要模块进行了简单的介绍。针对生产计划模块和计划调整模块遇到的问题提出了解决方案:讨论了柔性作业车间调度的问题,通过对柔性车间作业的工序约束建立了生产调度模型。在算法中着重讨论了班组分配和工序加工顺序问题,并提出了基于蚁群遗传的混合算法对该问题进行求解。同时又考虑了动态调度情况下的紧急工件插入问题,并给出了相应的解决方案。实验结果证明,该混合算法可以很好地解决该企业的生产调度问题,使企业产品能够按时保质保量的完成。本文算法的不足之处就是没有考虑大型公共设备的运输时间,这也是以后需要改进的地方。
[1] 黄肖玲,柴天佑.复杂生产过程计划调度级联模型在选矿MES中的应用研究[J].自动化学报,2011,37(9):1130-1139.
[2] 王丽红.基于混合蚁群算法Job-Shop调度问题的研究与实现[D].哈尔滨理工大学,2008.
[3] 张青.基于遗传算法的车间调度问题研究[D].长春理工大学,2012.
[4] 王海瑶,蒋增强,葛茂根.基于规则组合的Job Shop多目标柔性调度方法[J].合肥工业大学学报:自然科学版,2010(1):14-18.
[5] 姜桦,李莉,乔非,等.蚁群算法在生产调度中的应用[J].计算机工程,2005(5):76-78.
[6] 邓宇巍.热轧带钢生产调度模型与算法研究[D].上海交通大学,2007.
[7] 黄丽韶,朱喜基.基于MATLAB的蚁群算法求解旅行商问题[J].无线互联科技,2012(3):76-78.
[8] 宋毅.基于遗传算法的生产调度方法及其软件实现[D].浙江工业大学,2003.
RESEARCH AND APPLICATION OF PRODUCTION SCHEDULING SYSTEM IN STEEL STRUCTURE ENTERPRISES
Hua Jiwei1Tong Jingcui2Lei Zhaoming2
1(College of Computer and Information Engineering,Tianjin Normal University,Tianjin 300387,China)2(SchoolofControlScienceandEngineering,HebeiUniversityofTechnology,Tianjin300401,China)
A good production scheduling system can bring enormous benefits to the production of steel structure enterprises, however its production scheduling constraints are complex, and the optimisation are difficult too. For the scheduling problem, we proposed a hybrid ant-genetic algorithm-based production scheduling model. At the same time, we solved the problem of urgent workpieces insertion in dynamic scheduling case. Based on a certain steel structure enterprise in Hebei province, we studied the implementation of this production scheduling system. Experimental results showed that the application of hybrid ant-genetic algorithm in production scheduling of steel structure enterprise could improve production efficiency.
Steel structureProduction schedulingHybrid ant-genetic algorithmDynamic scheduling
2015-01-07。天津市高等学校科技发展基金计划项目(20120814);河北省科技支撑计划项目(13210307D)。花季伟,讲师,主研领域:工业物联网应用。佟静翠,硕士生。雷兆明,讲师。
TP3
A
10.3969/j.issn.1000-386x.2016.09.016

