改进的局部保持典型相关分析的无线传感器网络节点定位方法*

朱素文，曾宪华*，胡　梦

（1.重庆邮电大学计算机科学与技术学院，重庆400065；2.计算智能重庆市重点实验室，重庆400065）

改进的局部保持典型相关分析的无线传感器网络节点定位方法*

朱素文1，2，曾宪华1，2*，胡梦1，2

（1.重庆邮电大学计算机科学与技术学院，重庆400065；2.计算智能重庆市重点实验室，重庆400065）

利用接收信号强度（RSSI）进行无线传感器网络（WSN）定位是一类低成本定位方法。局部保持典型相关分析定位（LE-LPCCA）算法能通过节点间RSSI数据的相似度信息近似拟合WSN结构，取得了较高定位精度。但该算法只使用节点间相似性信息未保留信号空间和物理空间的相关性信息，且求解未知节点坐标时使用粗糙的质心法。针对以上问题，提出改进的局部保持典型相关分析定位（LE-ILPCCA）算法，该算法在样本训练阶段用平衡参数将数据的相似性和相关性信息进行融合，求取RSSI内在低维坐标表示的投影变换；在定位阶段，求解已知节点位置坐标和RSSI内在低维坐标之间存在的线性转换关系，获得未知节点的坐标。实验结果表明，本文算法与LE-LPCCA和LE-CCA相比定位精度高、稳定性强。

无线传感器网络；定位；典型相关分析；局部保持投影

EEACC：6150；7230doi：10.3969/j.issn.1004-1699.2016.10.019

无线传感器网络系统 WSN（Wireless Sensor Networks）主要应用于事件的监测，而事件发生的位置对检测来说是至关重要的。目前应用最为广泛的全球定位系统GPS（Global Position System）在卫星信号能到达的场所可以取得较好的定位效果，但其局限性较大，在室内环境或遮挡较严重的场所就不再适用。此外，GPS设备成本和能量消耗都较高，无线传感器网络又是一个资源受限的网络，能耗要求极为严格［1］。因此，利用网络中部分已知位置节点的信息对未知节点的位置进行估测的方法具有非常重要的研究价值。定位的目的是根据节点在全网络中收集到的接收信号强度 RSSI（Received Signal Strength Indicator）等数据，确定节点在网络中的物理位置。与其它定位技术相比，RSSI技术用于WSN定位中，所消耗的设备功率和成本较低，因此基于RSSI的定位算法被广泛应用。本文主要研究基于RSSI信息的定位方法。

借助统计学和流形学习对定位问题进行建模和算法设计一直是研究热点［2-7］。近年来，随着机器学习的发展，Pan Junfeng等提出基于核典型相关分析定位LE-KCCA（Location Estimation-Kernel Canonical Correlation Analysis）算法［8］，它集合CCA和核函数，对信号空间和物理空间求出一个统一的非线性映射，但未考虑WSN复杂多变的拓扑结构。顾晶晶等提出局部保持典型相关分析定位LE-LPCCA（Location Estimation-Locality Preserving Canonical Correlation Analysis）算法［9］，该算法将数据的局部结构信息引入到CCA中，能较好的拟合WSN结构，取得较高定位精度。陈祠等提出基于主成分分析的室内指纹定位模型［10］，它将对定位精度影响最大的一组“成分”作为指导定位的指纹，在减少计算量的同时提高定位精度。Lee等提出一种基于多维尺度支持向量回归的非测距定位算法［11］，该算法与标准支持向量回归不同，在不转化为多点定位问题的前提下实现多个输出，具有较好的鲁棒性和较高的定位精度。曾宪华等提出多粒度流形学习的定位方法［12］，该方法可以通过不同的筛选半径获得网络的不同粒度，灵活地刻画网络结构，降低计算复杂度的同时提高了定位精度。

文献［9］中提出的LE-LPCCA算法利用节点间RSSI相似度信息，即信号数据本身的内在特性，能够近似拟合复杂的WSN拓扑结构，从而取得较高的定位精度。但该算法只使用节点间相似性信息，未保留信号量和位置数据的相关性信息，这将导致数据相关性信息丢失、训练数据信息不够丰富，进而使RSSI内在低维坐标表示的投影变换求解不精准；且计算未知节点坐标时使用粗糙的计算方法—质心法，不能精确地获得未知节点的物理坐标。针对以上问题，本文做以下两点改进：（1）在训练阶段，目标函数中使用平衡参数α对样本的相似性信息和相关性信息进行融合，样本训练时数据信息会更为丰富、完整，可以使得到的RSSI内在低维坐标表示的投影变换更加精准；（2）在定位阶段，用训练阶段得到的投影变换对已知数据中高维的信号强度矩阵进行维度约减，求取已知节点位置坐标矩阵和降维后的信号量矩阵之间存在的较为精确的线性转换关系，未知节点的估测坐标将通过这一转换关系得到。与质心法相比，精确的线性转换关系在提高定位精度上起较大的作用。

1　相关工作

在节点功率相同、传送模式相似的前提下，传感器网络中任意两节点若相邻，则接收到同一信标节点所发射的信号强度也相似，所以物理空间和信号空间存在一一映射关系［8］。以本文其中一个实验的数据集来说明这一映射关系的合理性，表1为传感器网络节点位置与接收信号强度向量关系表。这里取8个点作为参考，其中信标节点个数为5，表1中1～2列为节点的横纵坐标、3～7列为每个节点的5维接收信号强度值，从表中很容易看出，位置相近的点接收信号强度向量也十分相似。无线传感器网络中的节点定位问题可以看作是：在RSSI向量构成的信号空间和纵横坐标（这里考虑二维空间定位）构成的物理空间寻找一个合适的映射关系。一旦找出该映射关系，就能通过未知节点的RSSI向量得到该节点的物理位置坐标。

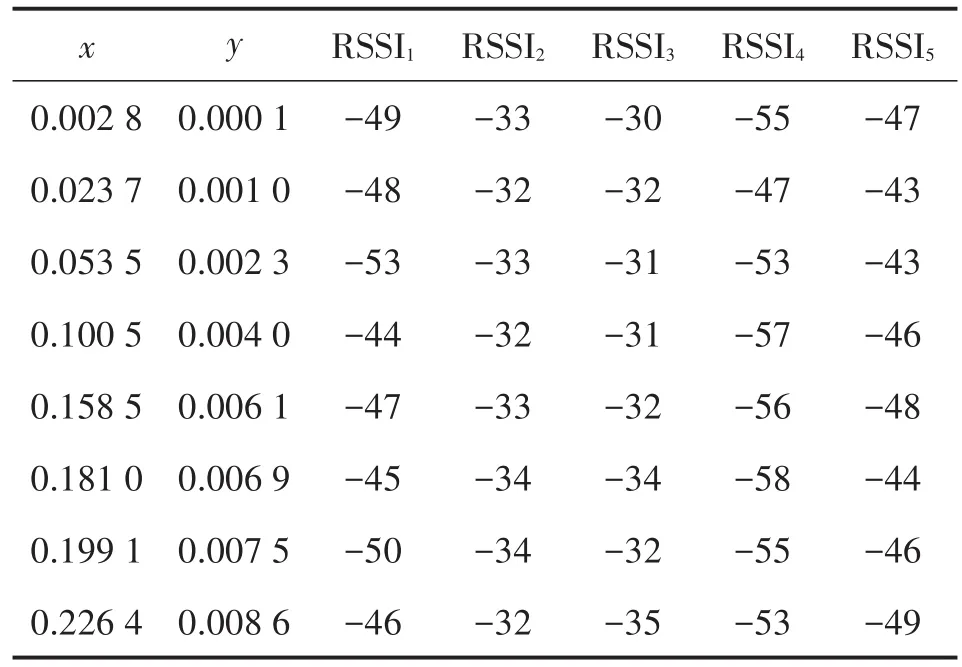
表1　传感器网络节点位置与接收信号强度向量关系表

对于一个无线传感器网络，大量的传感节点部署在区域C⊆R2内，其中m个接入点（AP）向非接入点周期性发送信号。寻求映射关系，需要收集n个位置已知的节点组成的位置坐标矩阵L=（l1，l2，…，ln）∈R2×n及其对应的从m个接入点接收到的信号强度向量组成的信号强度矩阵S=（s1，s2，…，sn）∈Rm×n；或某一移动节点沿某一轨迹移动，记录这一轨迹上n个坐标已知的位置并组成位置坐标矩阵L=（l1，l2，…，ln）∈R2×n及经过这n个位置点时所对应的信号强度向量，并组成信号强度矩阵S=（s1，s2，…，sn）∈Rm×n。以上为求解映射关系时所使用到的训练数据，当对未知节点求解时（即定位阶段），输入任一未知节点g的接收信号强度向量sg=（s1g，s2g，…，smg）T∈Rm×1，依据映射关系，就能求得该节点的位置估测坐标。

在机器学习领域，典型相关分析CCA（CanonicalCorrelation Analysis）［14］是构建两组数据间映射的经典方法，它是利用综合变量对之间的相关关系来反映两组指标之间的整体相关性的多元统计分析方法。给定一组成对样本（X，Y），其中X=［x1，x2，…，xn］∈Rs×n，Y=［y1，y2，…，yn］∈Rt×n，这里假定样本已中心化。CCA旨在为 X和Y分别寻找两组基向量（wx∈Rs，wy∈Rt），使随机变量wxTx和wyTy之间的相关程度最大。具体来讲，表示为求解式（1）相关系数ρ的最大值问题［14］：

式（1）定义的相关函数ρ关于wx和wy尺度无关，则CCA可表示为式（2）优化问题的解［14］：

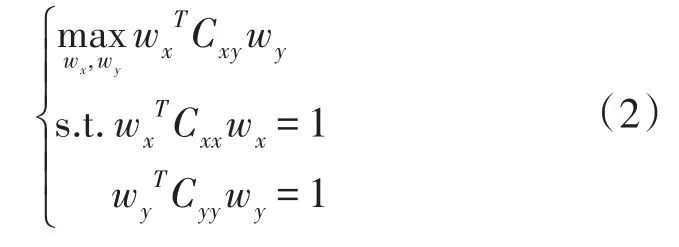
求解该最优化问题，文献［14］给出了详细的方法。通常可以得到一组基向量对（wxi，wyi）（i=1，…，d）及其对应的特征值，并将它们组成两个投影矩阵：Wx=［wx1，wx2，…，wxd］和 Wy=［wy1，wy2，…，wyd］。CCA可以为寻求信号空间和物理空间之间的映射关系提供依据，但它只能提取两组数据之间的线性关系，根据求得的投影矩阵使典型变量之间的相关性达到最大，而WSN定位问题中所使用的数据多数为高维、非线性的。

文献［9］中的LE-LPCCA算法针对LE-KCCA［8］对信号空间和物理空间求出一个统一的非线性映射、无法体现网络的分布特性这一不足，通过局部保持投影LPP（Locality Preserving Projections）［13］将网络的局部结构信息引入到CCA中，将原来的全局非线性问题转变成若干个局部的线性问题，计算每个邻域内的典型相关问题，通过优化目标函数计算得到一组投影基向量。LPP方法主要是通过一定的性能目标来寻找线性变换以实现对高维数据的降维，它注重数据内在的特性，即：复杂多变的无线传感器网络结构，旨在寻求隐含在高维数据中的低维流形结构，LE-LPCCA正是利用LPP这一特性，实现对网络拓扑结构的学习。下面具体介绍LE-LPCCA算法。

LE-LPCCA算法的输入为n个已知节点的位置坐标矩阵L=（l1，l2，…，ln）∈R2×n及其对应的接收信号强度矩阵S=（s1，s2，…，sn）∈Rm×n，未知节点g的接收信号强度向量sg=（sg1，sg2，…，sgm）T∈Rm×1；输出为未知节点g的位置坐标。

式中，ts和tl分别表示信号空间和物理空间的平均距离，这样的取法是为了使相似度矩阵更好地模拟网络拓扑结构。其中，

根据以上描述，WSN定位问题的目标函数为：

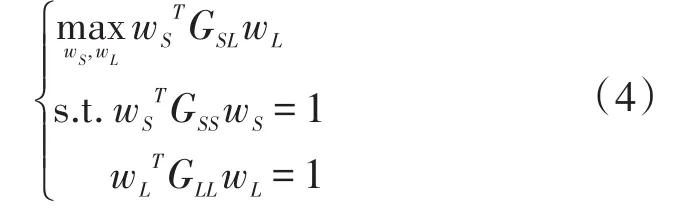
其中，GSL，GSS和 GLL的计算如下：GSL=SCSLLT，GSS=SCSSST，GLL=LCLLLT。CSL=DSL-GS∘GL，CSS= DSS-GS∘GS，CLL=DLL-GL∘GL。符号 ∘为算子；DSS（DLL，DSL）是大小为n×n的对称阵，其第i个对角元素等于矩阵GS∘GS（GL∘GL，GS∘GL）第i行（因其对称性，或第i列）元素之和。

其次，优化目标函数，求出投影矩阵WS和WL以及广义特征值λ，并对已知数据｛S，L｝作线性变换：，使数据降到二维空间，同样对未知数据进行线性变换，得到用式（5）计算未知点g与所有已知节点在线性变换后带有权重的欧式距离［8］：

其中，di表示第i个已知节点与g点的距离；λj表示第i个特征值的第 j个分量；表示第i个已知节点作线性变化后第 j个分量；表示g点作线性变化后的第 j个分量。

最后，计算未知节点K近邻节点：K个di（i=1，…，n）（第i个已知节点与g点的距离）的最小值及对应节点的物理坐标｛y1，y2，…，yK｝，其质心即为未知节点g的物理坐标。

该算法优化目标函数时只使用节点间相似度信息未保留信号空间和物理空间的相关性信息（协方差），数据间相关性信息的丢失会导致RSSI内在低维坐标表示的投影变换求解不精；且算法最后一步求解未知节点坐标时采用粗糙的计算方法—质心法，不能用较为精确的方式求解出未知节点坐标。

2　LE-ILPCCA定位算法

LE-LPCCA能够学习节点间相似度信息，进而对无线传感器网络结构近似拟合，从而取得相对高的定位精度，但该算法的目标函数只使用数据相似性信息未保留信号空间和物理空间的相关性信息，且求解过程中使用粗糙的计算方法—质心法。针对以上问题，本文提出改进的局部保持典型相关分析定位 LE-ILPCCA（Location Estimation-Improved Locality Preserving Canonical Correlation Analysis）算法，该算法分为两个阶段：训练阶段和定位阶段。训练阶段，用一个平衡参数将数据的相似性和相关性信息进行融合，对收集到的已知节点数据进行训练，从而求解目标函数得到合适的参数，即：较为精确的RSSI内在低维坐标表示的投影变换矩阵；定位阶段，根据已知节点数据和训练阶段得到的参数，求解已知节点位置坐标和RSSI内在低维坐标之间存在的较为精确的线性转换关系，并利用这一转换关系对未知节点的位置坐标进行计算。

2.1训练阶段

训练阶段是通过收集到的信号空间的RSSI数据和物理空间的位置坐标数据，计算两空间数据的相似性和相关性信息，在目标函数中用平衡参数将数据相似性和相关性信息进行融合，后对其进行优化求解，求取较为精确的RSSI内在低维坐标表示的投影变换矩阵。

训练阶段输入数据为：n个已知节点的位置坐标矩阵L=（l1，l2，…，ln）∈R2×n及其对应的接收信号强度矩阵S=（s1，s2，…，sn）∈Rm×n，p个未知节点的接收信号强度矩阵Sg=（sg1，sg2，…，sgp）∈Rm×p。

首先用式（6）分别计算信号矩阵和位置矩阵的集合内协方差矩阵CovSS、CovLL及两矩阵的集合间协方差矩阵CovSL。

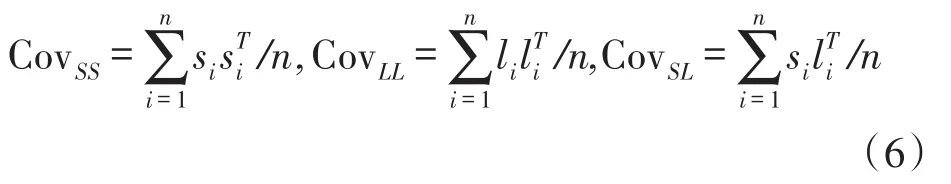
综上所述，WSN定位问题的目标函数为：

为了简化公式复杂性并方便接下来的求解运算，令：

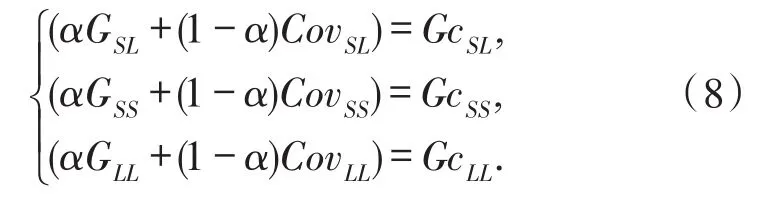
则式（7）可简化为式（9）：

对式（9）利用拉格朗日乘数法及消元解方程法，可得到如下特征值方程组：

最终得到如下广义特征值方程：

解方程并求解出更为精确的RSSI内在低维坐标表示的投影变换矩阵WS。以上为WSN定位问题中求解合适参数的训练阶段。

2.2定位阶段

当输入新的数据如：p个未知节点的接收信号强度矩阵Sg=（sg1，sg2，…，sgp），即进入WSN定位阶段时，使用训练阶段得到的投影矩阵WS对训练数据中高维的信号强度矩阵S进行维度约减，将其降到二维空间，作为候选二维信号强度矩阵PS。当对信号强度矩阵Sg中对应的每个未知节点gi（i=1，…，p）进行位置估测时，首先使用投影矩阵WS将高维信号强度向量sgi降到二维空间，再用式（5）计算gi和所有已知点（训练数据点）之间带有权重的欧氏距离［8］，并选取其中最短的K个距离所对应的候选二维信号强度矩阵和二维位置坐标矩阵中的K个列向量，分别组成两组含有K个元素的矩阵PS_K和L_K。通过以下推导建立这两个矩阵之间的线性转换关系W。gi的估测坐标将通过这一转换关系W得到。

设xi和分别表示二维位置坐标矩阵L_K和对应的二维信号强度矩阵PS_K，则它们之间的关系可以表示为xi=Wyi+b。其中，W是坐标转换矩阵，b是偏移量，是二维的，则：

分别任取xi和yi中的一个点做以下处理：

设yvs代表未知节点xv（v≠1，…，n）转换后的二维信号强度向量，则未知节点xv的位置坐标xvl求法为：

2.3LE-ILPCCA定位算法描述

文献［9］中提出的LE-LPCCA算法结合LPP将网络分布的局部信息和全局信息引入CCA中。然而，现有的LE-LPCCA存在信号空间和物理空间相关性信息丢失及求解未知节点坐标时使用粗糙质心法等问题。为弥补上述缺陷，本文提出改进的局部保持典型相关分析定位（LE-ILPCCA）算法，在LE-LPCCA算法的目标函数中增加信号空间和物理空间的相关性信息，用一个平衡参数将节点间相似性信息和两空间的相关性信息融合起来，进而求取一种RSSI内在低维坐标表示的投影变换，并根据已知节点位置坐标和RSSI内在低维坐标之间存在的较为精确的线性转换关系，获得未知节点的坐标。LE-ILPCCA算法的步骤如下：

算法1　LE-ILPCCA定位算法

图1为LE-ILPCCA定位算法示意图，灰色部分代表算法的训练阶段，主要是利用已知节点的数据和融合了协方差信息和相似度信息的目标函数，求解数据内在低维坐标表示的投影变换矩阵；蓝色部分代表算法的定位阶段，该阶段通过训练阶段得到的投影矩阵，计算训练数据及未知数据的二维空间表示，并利用带权值的欧氏距离求解未知节点的K个近邻点组成的信号强度矩阵和位置坐标矩阵，再根据这两个矩阵间的转换关系求得相对精确的线性转换关系矩阵，最后用转换关系矩阵和未知数据的二维空间表示得到该未知节点的位置坐标。

图1　LE-ILPCCA定位算法示意图

3　实验分析

3.1实验设计

为验证算法的性能，本文在两组模拟数据和一组真实数据上做实验，并分别与LE-LPCCA和典型相关分析定位（Location Estimation-Canonical Correlation Analysis，LE-CCA）算法作对比，LE-CCA是为了实验比较而设计的算法。为保证实验更细致地进行，本次试验中采用的变换间隔Δα为0.001，共循环1 001次。

两组模拟数据分别模拟的是平方区域C内随机分布及均匀分布的无线传感网络，网络中信号传播模型选择规则网络模型，无线电射程为环形，两网络的通信半径均为200 m。该模型与对数衰减模型（式（16））相比没有遮挡因子，式（16）中Pr（dist），Pr（d0），η，dist，Xσ分别表示与发射器距离为dist时的接收信号功率、距离为d0时从发射器接收到的功率、路径衰减指数、接收器与发射器之间的距离、遮挡影响因子［16］。两模拟网络中节点的接收信号功率可用式（17）表示。其中，Pt，Pl（d0）分别表示发射功率（0）、距离为d0（1 m）时的路径衰减功率（取值55），其中η取值为4。C内随机分布及均匀分布的网络中接入点个数分别为90和44，网络中所有节点个数分别为900和441。两网络分布图如图2和图3所示，其中红色点代表接入点，蓝色点代表非接入点。

图2　平方区域C内随机网络分布图

图3　平方区域C内均匀网络分布图

真实数据来源于瑞典皇家理工学院计算机科学与通信系。实验场景设置在400 m2的办公场所，其中包括一个走廊和若干个办公室。实验中一个具有可拆式外置天线的Wi-Fi接入点固定在试验场景内作为无线信号发射器，五个相同型号（TP-Link TL-WN722N）并装有可拆式外置天线的小型USB无线网络适配器安装在KUKA youBot上。这些无线网络适配器作为无线信号接收器与接入点通过2.4 GHz频率带宽的IEEE 802.11n相连接，无线适配器的通信半径为50 m。收集数据时，机器人以小于0.2 m/s的速度行驶并记录某些时刻的位置及其对应的无线信号强度值（dBm）［17］。

本文采用文献［18］的误差判定标准，通过所有节点的平均误差评判算法的性能。平均误差定义如式（18），其中，n，r，li，l͂i分别表示未知节点的个数、节点间单跳最大通信距离、未知节点的真实坐标和未知节点的估测坐标。

ave_error越小代表定位算法的精度越高。为了保证实验结果的准确性，每组实验都重复运行了20次以上。每组实验中，用作验证算法有效性的测试样本从未参与训练，且数量占总样本比例的30%。

3.2转换关系矩阵W及平衡参数α对平均定位误差的影响

以两组模拟数据集及一组真实数据为例，本文分析转换关系矩阵W及平衡参数α对定位精度的影响。当参数α为0时，本文算法可简化成与LE-CCA相近的算法，即与其唯一的不同之处在于求解未知节点坐标时使用较为精确的转换矩阵W而非质心法；同理当α为1时，本文算法可简化成与LE-LPCCA近似的算法，唯一的不同之处也和上述陈述一样。本文算法采用的邻域K是算法LE-ILPCCA（α=1）性能最优时的值，训练样本比例不同时K值也不同。每一个K值都对应一个最优的α值，当K值相同时，本文算法总是优于其它两种对比算法。

图4～图9中纵坐标均表示所有未知节点的平均定位误差，横坐标均表示训练样本百分比，它以10%为间隔从30%增加到70%。图4、图6、图8中蓝色曲线和红色曲线分别代表法算法LE-CCA和LE-ILPCCA（α=0）的平均定位误差变化趋势，图5、图7、图9中蓝色曲线表示算法LE-LPCCA的平均定位误差走势，红色曲线表示算法LE-ILPCCA（α=1）的平均定位误差变化情况。图4～图6的实验数据均为模拟数据，图8～图9为真实环境下的数据。模拟数据中，蓝色曲线和红色曲线在不同训练样本比例下平均定位误差的差值较为明显，差值为［0.061 2～0.690 2］；真实环境下平均定位误差的差值为［0.001 4～0.001 9］，虽然没有模拟数据中明显，但红色曲线依旧位于蓝色曲线之下。以下六个图中，对蓝色曲线和红色曲线走势分析发现：无论样本比例怎样变化，每个图中红色曲线总是低于蓝色曲线，即：使用转换关系矩阵W后平均定位误差整体降低。由此可以看出，无论α=0还是α=1转换关系矩阵W在提高定位精度上都起着重要的作用。

图4　转换矩阵W对算法LE-CCA的影响图（随机网络）

图5　转换矩阵W对算法LE-LPCCA的影响图（随机网络）

图6　转换矩阵W对算法LE-CCA的影响图（均匀网络）

图7　转换矩阵W对算法LE-LPCCA的影响图（均匀网络）

图8　转换矩阵W对算法LE-CCA的影响图（真实数据）

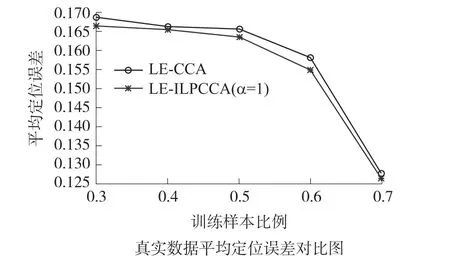
图9　转换矩阵W对算法LE-LPCCA的影响图（真实数据）

平衡参数α将数据的相似度信息和协方差信息结合起来，既使用信号空间和物理空间的相似性信息，又保留两空间之间的相关性信息，使训练样本信息更加丰富、完整。表2～表4为平衡参数α对平均定位误差的影响表，为了简化表格，平均误差值都用AEV（Average Error Value）表示。表2～表4的实验数据分别为随机网络、均匀网络和真实环境。

表2　平衡参数对平均定位误差的影响表（随机网络）

表3　平衡参数对平均定位误差的影响表（均匀网络）

表4　平衡参数对平均定位误差的影响表（真实环境）

分析3个表格的每一行（即在同一训练样本比例下），可以看出第4列最小的AEV总是比第2列和第3列都小，这表明在转换关系矩阵W减少了定位误差的基础上，平衡参数α又进一步提高了定位精度。

3.3实验结果

图10～图12中，横坐标均表示训练样本百分比（30%～70%），纵坐标表示所有未知节点的平均定位误差。蓝色曲线、绿色曲线和红色曲线分别表示算法LE-CCA、LE-LPCCA和LE-ILPCCA在训练样本密度不断增加的情况下节点平均定位误差的变化趋势。图10和图11都是模拟数据下的3种算法平均误差对比图，其区别在于图10是随机分布的网络，图11是均匀分布的网络。图12是真实数据下3种算法平均误差对比图。

图10　随机网络中3种算法平均误差对比图

图11　均匀网络中3种算法平均误差对比图

图12　真实数据中3种算法平均误差对比图

训练样本比例从30%以10%为增量增加到70%时，图10中，算法LE-CCA、LE-LPCCA和LE-ILPCCA的平均定位误差变化范围依次为［0.467 0～0.193 1］、［0.435 9～0.188 6］、［0.172 2～0.106 0］；图11中，3种算法的平均定位误差变化区间依次为［1.087 5～0.459 2］、［0.862 0～0.458 5］、［0.323 7～0.252 3］；图12中，3种算法的平均定位误差变化范围依次为［0.170 2～0.132 4］、［0.168 6～0.127 7］、［0.161 9～0.124 9］。图10和图11中平均定位误差的变化范围表示，LE-ILPCCA算法的平均定位误差明显低于LE-CCA和LE-LPCCA，图12中3种算法的平均定位误差之间的差值没有图10和图11明显，但LE-ILPCCA算法的平均定位误差仍旧低于其它两种。通过对比以上三个图可以看出，不论在模拟数据集还是真实数据集上，随着训练样本比例不断增加，节点的平均定位误差整体上都呈现不断减小的趋势，这是因为随着训练样本数量的增加，用作训练投影矩阵的样本信息更加丰富，从而对网络的分布特性和两空间之间映射关系的学习更准确。无论训练样本比例怎样变化，每一个图中的红色曲线都低于绿色曲线和蓝色曲线，这表示本文算法（LE-ILPCCA）在定位精度和算法稳定性上总是优于其它两种算法（LE-CCA和LE-LPCCA）。

最后，定量分析本文算法（LE-ILPCCA）与对比算法相比平均误差降低的百分比。表5～表7表示LE-ILPCCA与LE-CCA和LE-LPCCA相比平均定位误差降低的百分比数值，三个表的实验数据分别来源于：随机网络、均匀网络和真实环境。平均定位误差降低的百分比计算方法为：对比算法的平均定位误差减去本文算法的平均定位误差再除以对比算法的平均定位误差。为简化表格，平均误差降低百分比用AERP（Average Error Reduction Percentage）表示。分析三个表格中平均定位误差降低的百分比数值可以看出，LE-ILPCCA与对比算法相比：在模拟数据中，平均误差降低的百分比维持在39%～71%之间；在真实环境中，降低的百分比在1.06%～7.65%之间。真实环境中本文算法与对比算法相比平均误差降低的百分比没有模拟数据中高，这是因为真实环境的数据训练样本数量较多，LE-CCA和LE-LPCCA得出的平均定位误差已较低，维持在0.125 0～0.175 0之间，本文算法能进一步降低平均误差，但效果没有模拟数据中明显。

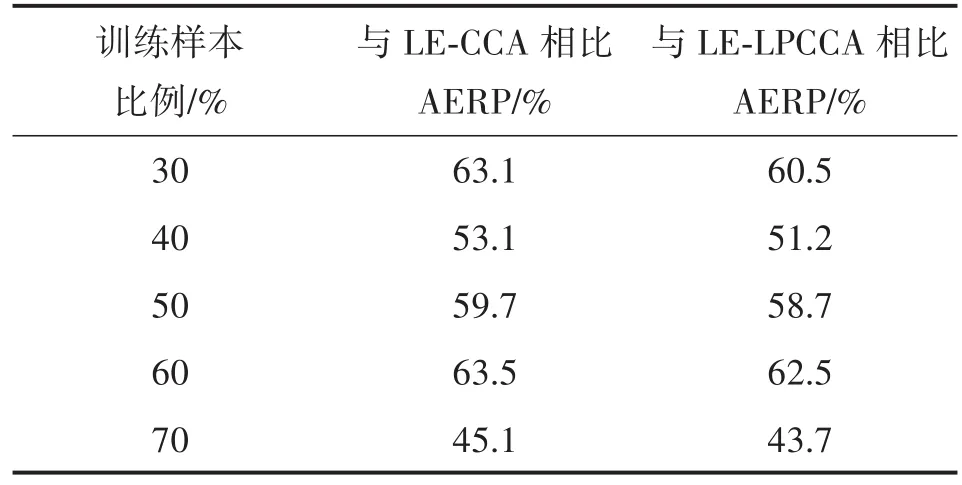
表5　本文算法与对比算法相比平均误差降低的百分比（随机网络）

表6　本文算法与对比算法相比平均误差降低的百分比（均匀网络）

表7　本文算法与对比算法相比平均误差降低的百分比（真实环境）

4　结论

本文提出改进的局部保持典型相关分析定位LE-ILPCCA）算法，主要是针对局部保持典型相关分析定位（LE-LPCCA）算法存在的两点不足：①训练阶段，目标函数中未保留信号空间和物理空间的相关性信息、仅使用节点间相似度信息，导致数据相关性信息丢失、数据内在低维坐标表示的投影变换不够准确；②定位阶段，求解节点位置坐标时使用较为粗糙的计算方法—质心法，不能精确地求解出节点位置坐标。本文算法弥补以上两点不足，主要改进之处在于：在样本训练阶段，同时使用已知数据的相似性信息和相关性信息，用平衡参数将两者融合起来，求取较为精确的数据内在低维坐标表示的投影变换；在定位阶段，根据已知节点位置坐标矩阵和RSSI内在低维坐标之间存在的线性转换关系，求解未知节点的坐标。本文在两组模拟数据及一组真实数据上做了实验，结果表明本文算法与LE-LPCCA和LE-CCA相比平均定位误差较低、性能较稳定。本文算法虽然克服以上两个缺点，但未找到一个鲁棒的算法来计算使节点平均定位误差最小的平衡参数，且该算法适用于二维空间定位问题，未扩展到三维空间中去，未来工作将在以上两个方面做改进。

［1］王营冠，王智.无线传感器网络［M］.北京：电子工业出版社，2012.

［2］Shang Y，Ruml W，Zhang Y，et al.Localization from Mere Connectivity［C］//Proceedings of the 4th ACM International Symposium on Mobile Ad Hoc Networking&Computing，Annapolis，Maryland，USA，2003：201-212.

［3］Patwari N，Hero I I I，Alfred O.Manifold Learning Algorithms for Localization in Wireless Sensor Networks［C］//International of Conference Acoustics，Speed，and Signal Processing，Quebec，Canada，2004：857-860.

［4］Samadian R，Noorhosseini S M.Probabilistic Support Vector Machine Localization in Wireless Sensor Networks［J］.ETRI Journal，2011，33（6）：924-934.

［5］Pan J J，Pan S J，Yin J，et al.Tracking Mobile Users in Wireless Networks via Semi-Supervised Colocalization［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2012，34（3）：587-600.

［6］陈淑敏，乔晓田，毛佳，等.基于接收信号强度（RSSI）的室内二次定位方法［J］.传感技术学报，2015，28（4）：572-577.

［7］杨文铂，邢鹏康，刘彦华.一种基于自适RSSI测距模型的无线传感器网络定位方法［J］.传感技术学报，2015，28（1）：137-141.

［8］Pan J J，Kwok J T，Yang Q，et al.Multidimensional Vector Regression for Accurate and Low-Cost Location Estimation in Pervasive Computing［J］.IEEE Transactions on Knowledge and Data Engineering，2006，18（9）：1181-1193.

［9］顾晶晶，陈松灿，庄毅.用局部保持典型相关分析定位无线传感器网络节点［J］.软件学报，2010，21（11）：2883-2891.

［10］陈祠，牟楠，张晨.基于主成分分析的室内指纹定位模型［J］.软件学报，2013，24（S1）：98-107.

［11］Lee J，Choi B，Kim E.Novel Range-Free Localization Based on Multidimensional Support Vector Regression Trained in the Primal Space［J］.IEEE Transactions on Neural Networks and Learning Systems，2013，24（7）：1099-1113.

［12］曾宪华，唐胜枰.基于多粒度流形学习的无线传感器网络定位方法［J］.传感技术学报，2013，26（8）：1152-1158.

［13］He X F，Niyogi P.Locality Preserving Projections（LPP）［C］//Neural Information Processing Systems，Vancouver，American，2004：96-103.

［14］Hardoon D R，Szedmak S，Shawe-Taylor J.Canonical Correlation Analysis：An Overview with Application to Learning Methods［J］.Neural Computation，2004，16（12）：2639-2664.

［15］Sun T K，Chen S C.Locality Preserving CCA with Applications to Data Visualization and Pose Estimation［J］.Image and Vision Computing，2007，25（5）：531-543.

［16］Rappaport T S.Wireless Communications：Principles and Practice［M］.New Jersey：Prentice Hall PTR，1996.

［17］Ramviyas Parasuraman，Sergio Caccamo，Fredrik Baberg，Petter O-gren，CRAWDAD dataset kth/rss（v.2016 01 05），traceset：indoor，downloaded from http：//crawdad.org/kth/rss/20160105/indoor，doi：10.15783/C7088F，Jan 2016.

［18］王成群.基于学习算法的无线传感器网络定位问题研究［D］.浙江：浙江大学，2009.

朱素文（1991-），女，重庆邮电大学计算机学院硕士研究生，主要研究方向为无线传感器网络定位、流形学习等，zhusuwen@foxmail.com；

曾宪华（1973-），男，四川攀枝花人，2009年获得北京交通大学计算机软件与理论专业博士，现任重庆邮电大学计算机学院教授，硕士生导师，计算机学会会员，主要研究方向为机器学习和计算机视觉等，zengxh@cqupt.edu.cn；

胡梦（1992-），女，重庆邮电大学计算机学院硕士研究生，主要研究方向为无线传感器网络定位、流形学习等，humeng1016@foxmail.com。

Improved Locality Preserving Canonical Correlation Analysis Node Localization Method in Wireless Sensor Networks*

ZHU Suwen1，2，ZENG Xianhua1，2*，HU Meng1，2
（1.College of Computer Science and Technology，Chongqing University of Posts and Telecommunications，Chongqing 400065，China；2.Chongqing Key Laboratory of Computational Intelligence，Chongqing 400065，China）

Location methods in wireless sensor networks（WSN）by received signal strength indicator（RSSI）are relatively inexpensive.Location Estimation-Locality Preserving Canonical Correlation Analysis（LE-LPCCA）can fit the structure of WSN approximately using RSSI similarity among nodes and achieve high localization accuracy，but it only uses data similarity while ignoring data dependency between signal and physical space，and employs rough centroid method.As to problems above，this paper proposes Location Estimation-Improved Locality Preserving Canonical Correlation Analysis（LE-ILPCCA）method.In training phrase，it combines data similarity and dependency using a balance parameter to compute more precise projection transformation of RSSI inner lower dimensional coordinates；in localization phrase，it calculates location of unknown nodes utilizing accurate transformational relation between position coordinates and RSSI inner lower dimensional coordinates of known nodes.Experimental results show that our method has a higher accuracy and stability than LE-LPCCA and LE-CCA.

wireless sensor networks；localization；canonical correlation analysis；locality preserving projections

TP393

A

1004-1699（2016）10-1579-10

项目来源：国家自然科学基金项目（61075019）；2015年重庆市研究生科研创新项目（CYS15173）

2016-03-20修改日期：2016-04-21