基于拟态有限体积法的频率域可控源三维正演计算

彭荣华， 胡祥云， 韩波， 蔡建超

1 中国地质大学(武汉)地球物理与空间信息学院， 武汉　430074 2 不列颠哥伦比亚大学地球、海洋与大气科学学院， 温哥华 V6T 1Z4， 加拿大 3 中国海洋大学海洋地球科学学院， 青岛　266100



基于拟态有限体积法的频率域可控源三维正演计算

彭荣华1,2， 胡祥云1*， 韩波3， 蔡建超1

1 中国地质大学(武汉)地球物理与空间信息学院， 武汉430074 2 不列颠哥伦比亚大学地球、海洋与大气科学学院， 温哥华 V6T 1Z4， 加拿大 3 中国海洋大学海洋地球科学学院， 青岛266100

大规模地球物理电磁数据的定量解释需要发展高效、稳定的三维正反演算法.本文通过求解离散化的三维电场矢量Helmholtz方程，实现了基于有限体积法的频率域可控源电磁(CSEM)三维正演算法.为模拟具有强电性差异的三维电性介质，该算法采用拟态有限体积法(MFV)对Maxwell方程组进行离散化；另外，为获得稳定、高精度的正演数值结果，采用直接矩阵分解技术来求解离散所得到的大型稀疏线性方程组.对于具有多个发射源的CSEM测量来说，一次矩阵分解结果能够用于同频率下所有场源的正演计算.为降低场源奇异性及边界条件对数值精度的影响，采用虚拟场源校正技术，避免了散射场公式中在构建场源项时所需的大量时间.对于具有多个频率的CSEM的模拟计算，采用分频并行策略来加快三维正演计算.最后，通过与一维层状模型及三维模型的数值结果的对比验证了本文所开发的正演算法对频率域CSEM模拟计算的准确性及有效性，表明该正演算法能够有效应用于三维介质的数值计算.另外，对于多频率CSEM的并行测试结果表明基于分频并行策略的并行计算能够显著地降低正演计算时间.

可控源电磁法； 有限体积法； 虚拟场源校正技术； 三维正演； 直接分解法

An important step in this 3D modeling scheme is to solve the large linear equation system resulting from MFV discretization. In order to obtain stable and accurate numerical solutions, the linear equation system is solved by a direct-matrix solver, namely MUMPS, which is more robust than commonly used iterative solvers (e.g, Krylov subspace iterative techniques) for numerically difficult cases. The algorithm is very suitable for multi-source CSEM modeling by separating the solving process into a single expensive matrix factorization and relatively inexpensive forward backward substitutions for many right-hand sides.

For total-field formulation, dense gridding in the vicinity of source points is usually required to mitigate source singularities, and extra padding cells at the boundaries are needed to meet boundary conditions. Both of them can quickly increase the size of the linear equation system to be solved, making it computationally expensive for direct solutions. To avoid substantial increase of the size of the discretized model, a source correction technique is applied to reduce source singularities and boundary effects. In addition, considering the independence of computation for different frequencies, a parallel forward modeling scheme based on frequency partition is implemented to speed up the simulation of multi-frequency CSEM problems.

Numerical experiments have been carried out to evaluate the performance of our forward modeling algorithm. Numerical solutions using this algorithm show good agreement with quasi-analytic solutions for 1D layered models, and numerical errors are significantly reduced with source correction in the vicinity of source points. In addition, comparison of simulated data generated by our algorithm to published 3D data for a typical marine 3D model validates our algorithm. Besides, statistical results demonstrate that parallel computing based on simple frequency partition approach can achieve nearly linear speedup due to the independence of computation between frequencies for multi-frequency CSEM simulation.

1　引言

频率域可控源电磁法(controlled-source electromagnetic method，CSEM)由于具有勘探深度大，分辨力高且野外抗干扰能力强等优点，经过30多年快速发展，目前已被广泛应用于包括陆地、海洋及航空等领域内的油气、矿产资源勘探和近地表地质勘查.随着电磁仪器、数据采集技术以及解释方法的快速发展，可控源电磁法在复杂地质环境下的三维勘探成为当前电磁勘探的重要趋势及研究热点.在电磁数据的处理解释中，反演是必不可少的步骤，而正演计算是反演的核心.因此，电磁数据的定量解释首先需要发展有效的正演算法.从数值模拟的角度来说，目前常用于三维电磁正演的数值方法主要包括：积分方程法(Avdeev et al., 2002；Hursán and Zhdanov, 2002；Zhdanov et al., 2006；Avdeev and Knizhnik, 2009)、有限差分法(Mackie et al.,1994；Newman and Alumbaugh, 1995；Smith, 1996；Weiss and Newman, 2002；沈金松, 2003； Streich, 2009)、有限体积法(Haber and Ascher, 2001；Weiss and Constable, 2006； 杨波等, 2012； Jahandari and Farquharson, 2014；韩波等, 2015a)和有限单元法(Badea et al., 2001； 徐志锋和吴小平, 2010；Schwarzbach et al., 2011；Puzyrev et al., 2013； Ansari and Farquharson, 2014；李勇等, 2015；杨军等, 2015).另外，其他方法如伪谱法(Huang et al., 2010; Liu et al., 2013)、Lanczos谱分解法(Knizhnerman et al.,2009)也被广泛用于三维电磁正演问题的求解.有关电磁法三维正演方面进展的综述可以详见(Avdeev, 2005；Börner, 2010).总体来说，目前三维正演算法研究的重点在于提高精度和计算效率.

CSEM正演中常采用散射场方法来避免场源的奇异性，然而构建散射场的场源项需要计算几乎每个离散网格采样点处的一次电场或磁场.对于三维问题，离散网格中的电场或磁场采样点个数大约是网格数的3倍，很容易达到几百万甚至上千万.因此构建散射场场源往往需要大量的时间，随着发射场源的增加，甚至有可能超过解线性方程需要的时间(韩波等, 2015b).相较之下，总场方法直接对物理场源离散化，不存在这个问题.但总场方法中一般需要在物理场源附近加密网格来削弱场源奇异性的影响，大量网格数同样会导致大量的计算时间.除了加密网格以外，还可采用场源校正技术等手段来降低场源奇异性的影响.

正演计算中的一个关键步骤是求解离散化后产生的大型线性方程组.在早期受限于计算机内存，三维正演中大型线性方程组几乎都采用对内存需求极低的Krylov子空间迭代法.随着大型稀疏矩阵分解算法的不断优化(Amestoy et al., 2001，2006； Li, 2005； Schenk and Gärtner, 2006)以及计算机硬件技术的快速发展，利用直接解法求解三维正演的大型线性方程组成为可能.与迭代解法相比，对于同一线性方程组，直接解法通常需要消耗更多的计算内存和更长的计算时间.尽管如此，直接解法相对于迭代解法有两大显著优点：一是求解时间和精度基本不受系数矩阵的条件数影响，因此网格的剖分方式或介质的电性差异对正演算法影响很小，使得求解精度更高，正演算法更稳定；另一个是直接解法的主要开销集中在系数矩阵的分解阶段，对于单一频率多个场源位置的问题，只需进行一次矩阵分解加上多次计算量极小的前代-回代过程即可，而不像迭代解法对每个频率每个场源都要单独求解，因此直接解法特别适合具有多个场源的CSEM三维模拟(Oldenburg et al.，2013).正因为这些优点，基于矩阵分解的直接解法最近几年开始应用于CSEM三维正演计算(Streich, 2009；Chung et al., 2014；杨军等, 2015).

本文采用拟态有限体积法(Mimetic Finite Volume, MFV)，通过求解离散化的三维电场矢量Helmholtz方程，实现了频率域CSEM三维正演算法.为获得稳定且高精度的数值结果，采用直接矩阵分解法来求解离散所得到的大型稀疏线性方程组；为消弱场源奇异性及边界条件的影响，采用场源校正技术来提高求解精度.对于多频率正演问题，采用分频并行策略来降低正演计算时间；最后通过多个理论合成模型正演计算测试，验证了本文所开发的正演算法对频率域CSEM模拟计算的准确性及有效性.

2　方法理论

2.1控制方程

在CSEM所采用的频率范围内，位移电流的影响可以忽略不计.假定时谐因子取为eiwt，则频率域Maxwell方程组可表示为

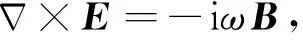
(1)

(2)

其中，E为电场强度(V·m-1)，B为磁感应强度(T)，ω为角频率(rad/s).σ为介质电导率(S·m-1)，对于各向同性介质，σ为标量.μ0为真空中磁导率(H·m-1). Js为外部激发场源的电流密度(A·m-2).对(1)式取旋度并将其带入(2)式，消去磁感应强度B，得到关于电场E的二阶矢量Helmholtz方程为

(3)

2.2拟态有限体积法

为求解方程(3)，本文采用拟态有限体积法(MFV)来对连续的Maxwell方程组进行离散化.MFV方法的最大特点是能够对连续的微分算符进行精确的离散模拟，并确保离散化后的矢量场仍然满足其对应的连续形式的矢量性质及物理特性(Hyman and Shashkov, 1999a, b).如离散化的电磁场的能量守恒能够自动满足，有效避免了伪解的产生.对于正交规则网格及各向同性介质来说，该离散化方法与常用的交错网格有限差分法(Staggered Finite-Difference, SFD)相一致(Smith, 1996).尽管最近也有将非正交交错网格有限差分法应用于电磁数值模拟的研究(邱稚鹏等，2013)，但MFV适用范围更广，其不仅对于非正交网格同样适用(Hyman and Shashkov, 1997)，而且对于具有高度电性差异及各向异性介质，MFV能够自然地得到对称的离散化形式(Hyman et al., 1997；Haber and Ruthotto, 2014)，这对于复杂三维介质的模拟十分有效.

为获得Maxwell方程组的离散形式，首先考虑方程(1)和(2)的弱解形式为(Hyman and Shashkov, 1999a)：

(4)

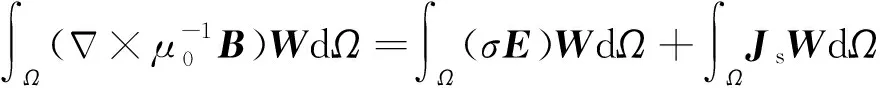
(5)

其中W和F分别为与电场E和磁感应强度B属于相同Hilbert空间的任意测试函数(Hyman and Shashkov, 1999a).对(5)式左端项进行分部积分，可得公式为

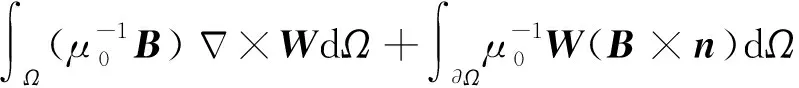
(6)

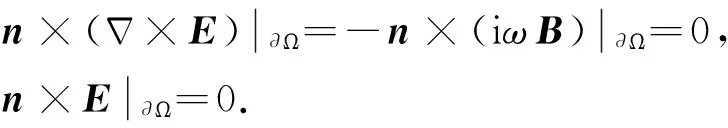
(7)

将(6—7)式代入到(5)式中，得到公式为

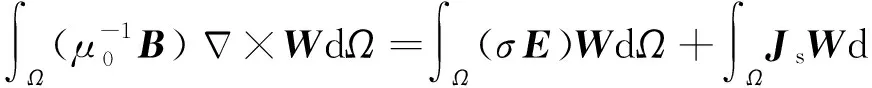
(8)

由于MFV是在离散单元的控制体积内进行积分，因此正交结构网格(Weiss and Constable, 2006；韩波等, 2015a)、半结构网格(Haber and Heldmann, 2007)和非结构网格(Jahandari and Farquharson, 2014)都能用来对(4)式和(8)式的积分进行离散化.本文采用基于Yee网格(Yee, 1966)的交错网格.图1展示了交错网格电磁场采样方式及电场分量和磁场分量各自的控制体积.其中电场定义在单元棱边的中心，磁感应强度定义在单元面的中心，介质电导率和磁导率定义在单元中心.

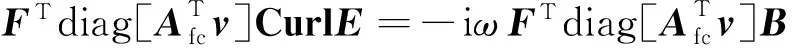
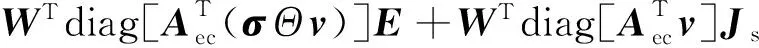
(10)

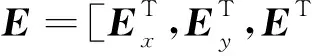
由于F和W为任意的网格测试函数，将(9)式代入(10)式并进行简化可得(3)式的离散形式为

(CurlTMfμCurl+iωMe σ)E=S，

(11)

其中

(11)式可简化成大型线性方程组为

(12)

其中系数矩阵A为稀疏、正定、对称复矩阵.图2给出了网格数为5×5×5的模型的MFV离散所得到的系数矩阵A的稀疏结构.

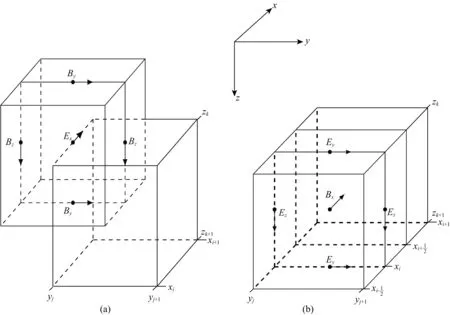
图1　电磁场分量交错采样方式及其控制体积(a) 电场x分量采样位置及其控制体积； (b) 磁场x分量采样位置及其控制体积.Fig.1　Staggered discretization of MFV(a) Integration volume for x-component of electric field； (b) Integration volume for x-component of magnetic field.

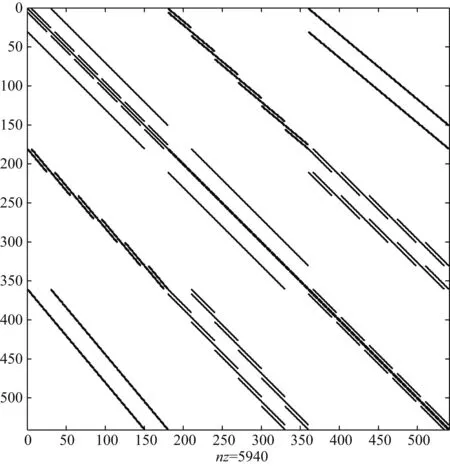
图2　网格数为5×5×5的模型的MFV离散线性方程系数矩阵的稀疏结构Fig.2　Sparse structure of coefficient matrix A resulted from MFV discretization on a 5×5×5 staggered grid

2.3虚拟场源校正技术

在可控源电磁法中，由于外加场源的存在，待求解的电磁场在场源附近会发生急剧变化，场源的奇异性会极大降低数值计算结果的精度.目前主要有两种处理方法来降低场源奇异性的影响. 第一种方法是采用散射场公式(Newman and Alumbaugh, 1995；Streich, 2009；韩波等, 2015a)，将待求解的电磁场分解为由参考模型(一般为均匀空间或一维层状模型)在外加场源激发下所产生的一次场和三维模型所产生的二次场的叠加.由于外加场源已包含在一次场的计算中，二次场的场源不再具有奇异性.另一种是基于电磁场总场公式，通过对场源点附近进行网格加密的方法来减少场源奇异性的影响(Plessix et al., 2007).

在散射场公式中，为避免计算二次场时出现场源的奇异性，必须确保选择的参考模型的电阻率与场源点附近的电阻率一致.对于海洋CSEM测量来说，由于发射场源一般位于海水中，一般容易满足该条件.但对于陆地CSEM测量来说，通常CSEM勘探会在较大测区内布设多个发射位置(Streich et al., 2011)，当场源处的电阻率发生变化时，需要求解不同参考模型的一次电磁场响应，从而增加计算量.另外，在散射场公式中，每个场源处都需要计算三维空间内所有电磁场采样点处的一次电磁场来构建场源项或进行总场合成.随着发射场源位置的增加，场源项的构建所消耗的时间会快速增加，甚至会超过系数矩阵分解所消耗的时间(韩波等, 2015b).与之对比，在总场公式中，网格加密的策略虽然能够降低场源奇异性的影响，但与此同时会显著地增加待求解的未知量个数，从而增大计算开销，降低求解效率.另外，为满足边界条件，无论是采用散射场公式还是总场公式，通常都需要将计算区域的外边界设置得足够远，这使得待求解的方程组会非常巨大.

为降低场源奇异性及边界条件对数值精度的影响，本文采用虚拟场源校正技术(Pidlisecky et al., 2007)来对总场控制方程(11)式中的源项进行校正，避免了在场源点附近进行网格局部加密所造成的计算量的增大.Pidlisecky等(2007)、Pidlisecky和Knight(2008)将该校正技术运用到直流电阻率的正演计算中，取得了很好的效果.为得到校正后的场源项，考虑存在解析解的均匀半空间模型σ0，利用上节发展的有限体积法对其离散化可得公式为

(13)

其中系数矩阵A(σ0)和右端项S0均由(11)式确定.假设E0是模型σ0在外加场源Js激励下的网格采样点处的电场响应，可通过解析求解很容易得到(Ward and Hohmann, 1988)，由于离散化误差及边界条件的影响，待求解的电场分量E与真实的电场响应E0会有一定差异.此时，我们可以得到场源校正量为

(14)

将(14)式所得到的场源校正量添加到(12)式右端，得公式为

(15)

通过求解(15)式便可以得到待求解的电场值.

2.4大型线性方程组的求解

由于离散后所得到的系数矩阵为稀疏、正定、对称复矩阵，本文通过调用基于多波前分解算法的MUMPS (Amestoy et al., 2001，2006)线性运算库对其进行LDLH分解，然后计算所有发射场源的CSEM电磁响应.有关MUMPS的运算效率及与迭代法的对比可参考Streich(2009)和Oldenburg等(2013)，另外关于MUMPS的求解精度、稳定性及内存需求等性能的详细分析，可参考韩波等(2015b).

2.5多频率并行计算

为增大勘探深度及提高数据空间分辨率， CSEM测量中通常会采集多个频率的数据.对于三维正演来说，为降低计算时间，通常需考虑对其进行并行计算.一种思路是利用并行矩阵分解算法对多个频率依次进行求解.由于矩阵并行分解算法涉及到不同进程之间大量的通信需求，并行效率不甚理想；并且，随着并行进程数的增加，总的内存消耗也会迅速增加(Pardo et al., 2012；韩波等, 2015b).对于频率域CSEM来说，考虑到不同频率之间的正演计算是相互独立的特征，在计算资源允许的条件下，可以对多个频率同时进行并行矩阵分解计算.Grayver等(2013)的测试结果表明，分频并行策略比采用矩阵并行分解算法依次对多个频率进行分解计算的效率要高很多.因此本文采用分频并行策略，将所有频点尽可能均匀地分配到所有进程中进行并行计算.

并行程序采用主从并行模式.其中主进程作为控制节点，负责模型网格、收发参数的发送以及计算任务的分配，并对各子进程的计算结果进行回收以及结果的输出，不参与计算；各子进程负责从主进程处接受计算任务并将计算结果发回给主进程.在整个并行计算过程中，各子进程只与主进程进行通信.由于本文所使用的并行计算平台计算资源(可调用的计算节点数和计算内存)的限制，在子进程中，对于每个频点的计算，并未采用矩阵并行分解算法.当分配有多个频点时，需依次对多个频率进行分解计算.整个并行算法的计算流程如图3所示.

图3　CSEM 正演并行计算流程图Fig.3　Flowchart of 3D parallel CSEM forward modeling

3　理论模型计算

本节通过对多个理论模型的正演数值结果的对比分析来检验本文所开发的正演算法对频率域CSEM模拟计算的准确性及有效性.

3.1一维层状模型的对比测试

为了验证本文所开发的CSEM三维正演算法的准确性，首先考虑具有准解析解的一维层状模型.图4a是海洋CSEM中用于模拟高阻油气层的标准模型(Constable and Weiss，2006).为模拟强电性差异，油气层电阻率设为1000 Ωm，厚度为100 m，顶部距海底1000 m；海底沉积层电阻率为1 Ωm，海水层厚度为1000 m，电阻率为0.33 Ωm.图4b为典型陆地一维层状模型.电阻率为100 Ωm沉积层中包含一层电阻率为10 Ωm的低阻目标层，该目标层顶部埋深200 m，厚度为400 m.所有模型的空气层电阻率均取109Ωm.本文所有计算均在一个小型并行机上完成.该小型并行集群系统配置有8个计算节点，每个计算节点含有2个4核Intel○RXeon○RE5410型处理器，主频为2.33 GHz，每个计算节点配置有32G内存.操作系统为CentOS 5.5.层状模型的拟解析解均通过Dipole1D程序(Key，2009)求得.

对于海底层状模型(图4a)，其观测系统设置为：电偶极子位于海底上方100 m，发射频率取0.25 Hz和1 Hz，电流强度为1A.接收器位于海底表面，布设方向与偶极方向一致(inline观测方式).模型剖分网格数为132×52×52.图5给出了不同频率下Ex分量和By分量的振幅-收发距(Magnitude Versus Offset, MVO)曲线与相位-收发距(Phase Versus Offset, PVO)曲线的MFV三维数值解与解析解的对比.从图中可以看出，不同频率的电磁场分量的MFV数值解与解析解均高度一致.图6则给出了MFV解相对于解析解的误差情况.当未进行场源校正时，可以看到在发射偶极附近(收发距小于1000 m)，电磁场的各个分量均具有较大的误差，振幅最大误差可达10%左右，相位最大误差可达2°，这主要是由于场源的奇异性造成的.需要说明的是，为降低待求解的线性方程组的尺寸，减少直接求解的计算量，本文并未在场源点附近进行精细的网格加密来降低场源奇异性的影响.当采用场源校正技术后，在场源附近，场源奇异性对于数值精度的影响会迅速降低，振幅最大误差降为5%以内，相位最大误差降为1.5°以内.另外，随着收发距的增加，场源奇异性的影响迅速降低，误差也随之迅速减小，电磁场分量的振幅误差降为2%以内，相位误差在2°以内.对于海洋CSEM来说，近场区内(收发距小于1000 m)一次场占据主导地位，一般并不包含海底目标层信息(Zhdanov et al., 2014).另外，从数值计算结果对比来看，场源奇异性对于远场区的计算精度影响有限，因此采用总场公式对于海洋CSEM的正演计算是完全可行的.

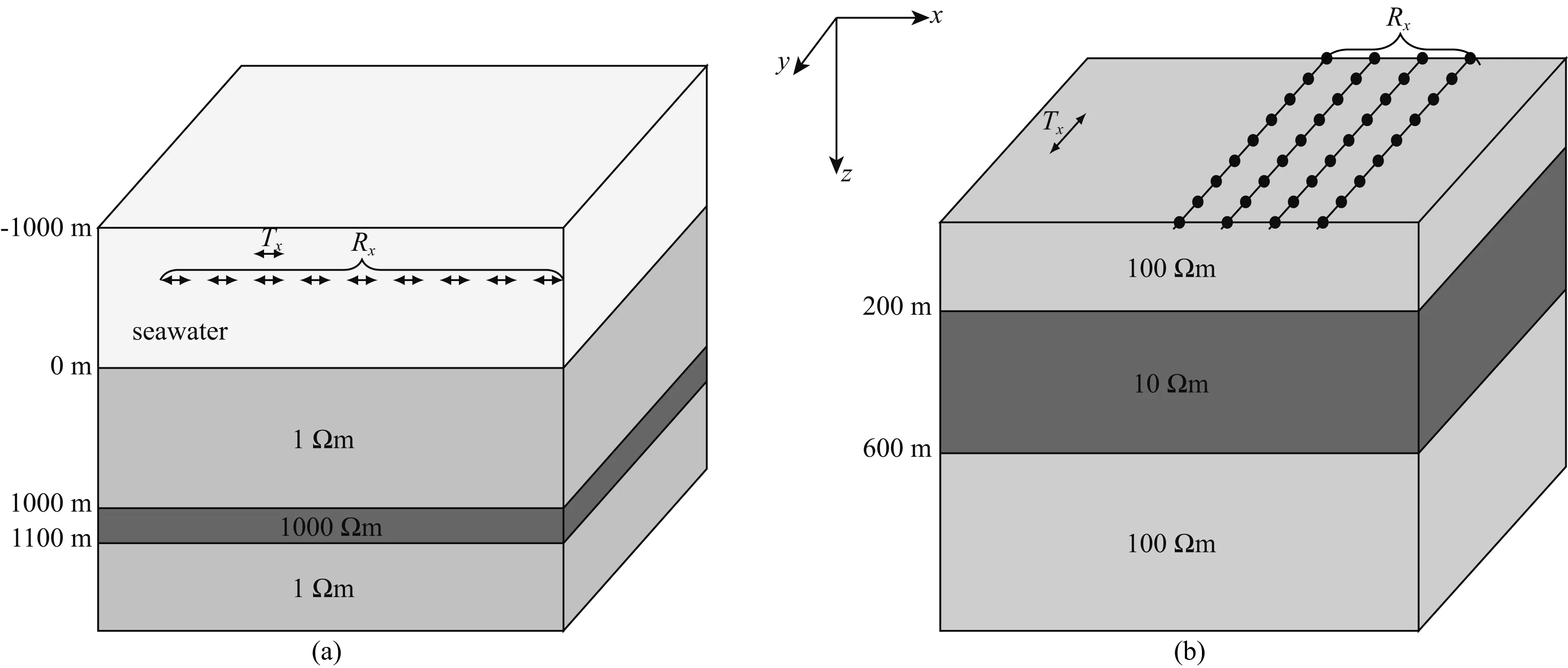
图4　海洋(a)及陆地(b)一维层状模型Fig.4　Sketches of (a) marine-based and (b) land-based 1D layered models

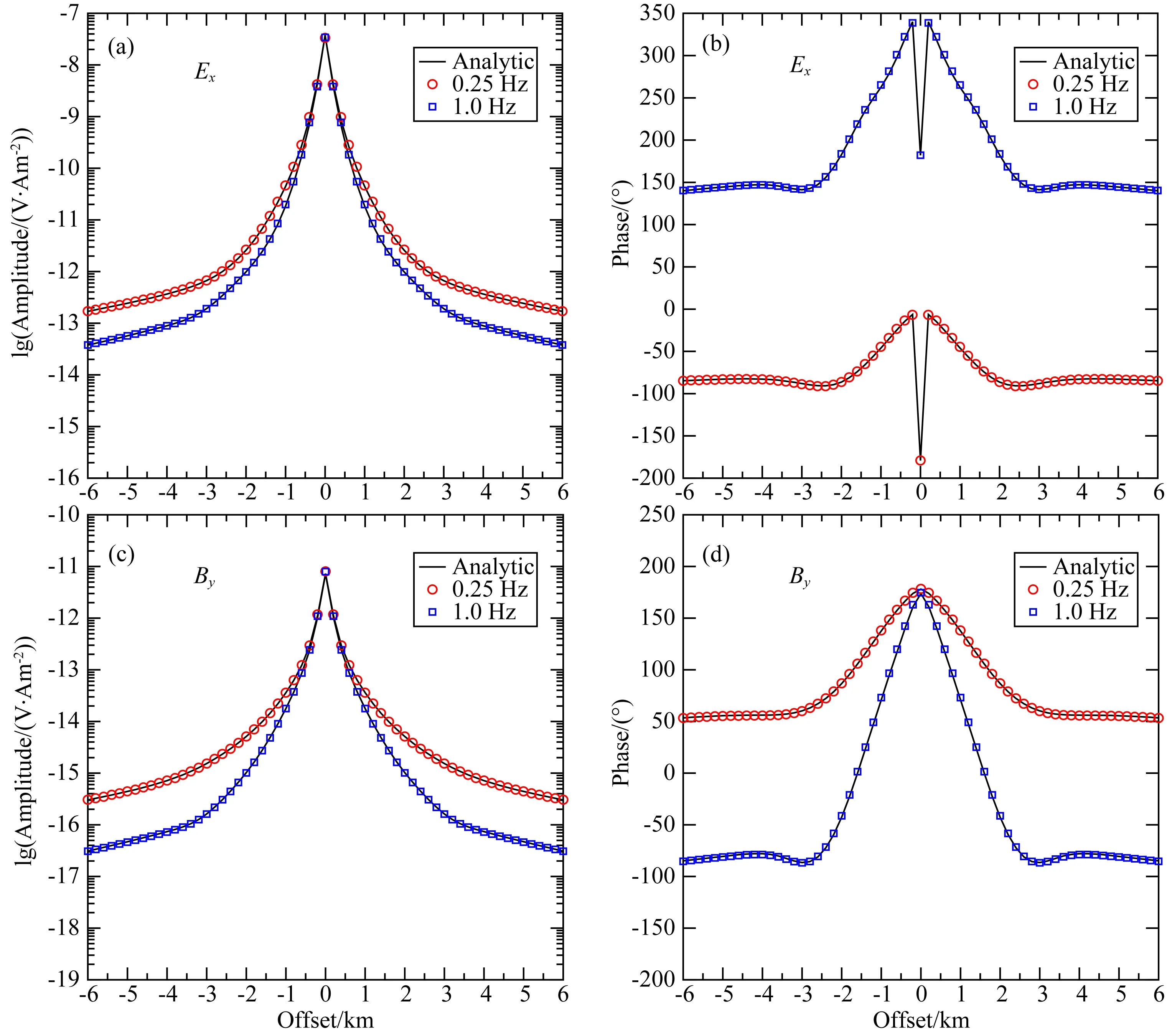
图5　海洋层状模型CSEM数值解与拟解析解对比(a)(c)为电磁场分量的振幅，(b)(d)为对应电磁场的相位.Fig.5　Accuracy comparison between MFV numerical solutions and quasi-analytic solutions for marine 1D layered model(a)(c)are amplitudes of field components,(b)(d)are corresponding phases.

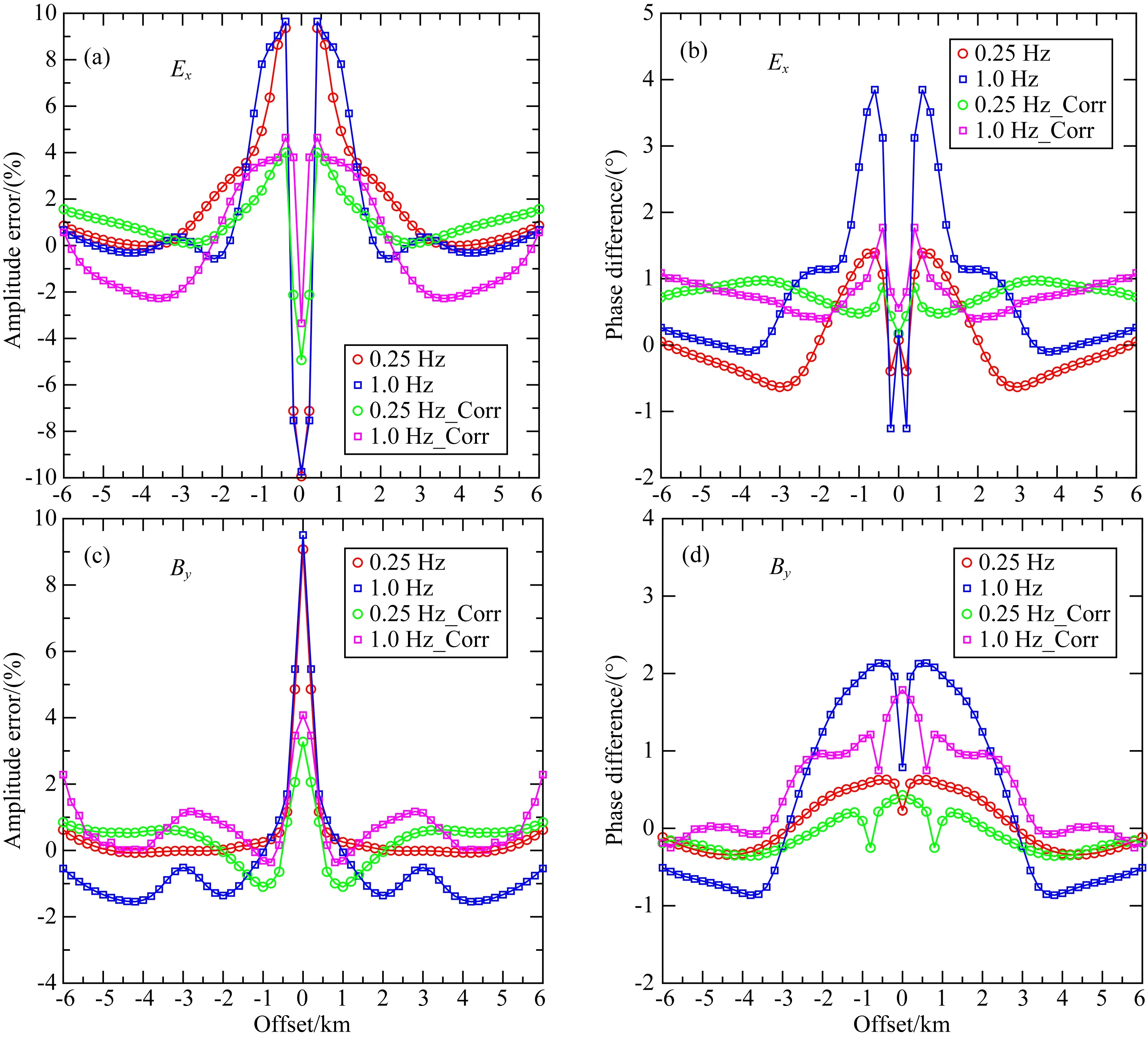
图6　海洋层状模型CSEM数值解相对于拟解析解的误差(a)(c)为电磁场分量振幅的相对误差，(b)(d)为对应电磁场的相位差异.Fig.6　Errors between MFV numerical solutions and quasi-analytic solutions for marine 1D layered model(a)(c)indicate relative errors in amplitude,(b)(d)are corresponding phase difference.

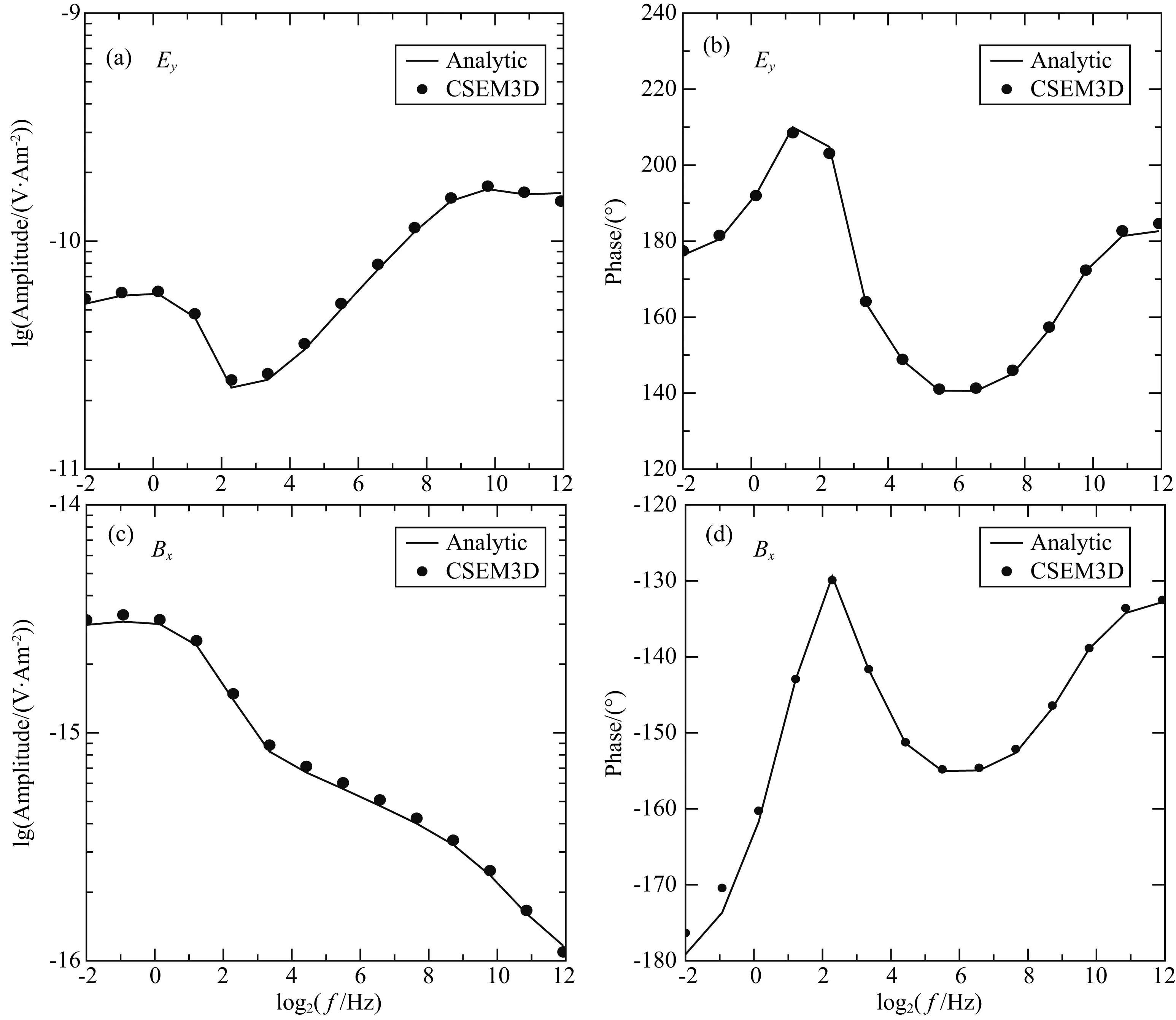
图7　层状模型CSEM数值解相对于拟解析解的误差(a)(c)为电磁场分量的振幅，(b)(d)为对应电磁场的相位.Fig.7　Accuracy comparison between MFV numerical solutions and quasi-analytic solutions for land 1D layered model(a)(c)are amplitudes of field components,(b)(d)are corresponding phases.

对于陆地层状模型(图4b)，观测系统采用可控源音频大地电磁法(CSAMT)(底青云和王若，2008)的观测方式.其中发射源为1000 m的接地导线，发射频点数为14个，频率在0.25～4096 Hz之间呈对数等间隔分布；测线平行于发射源布设.模型剖分网格数为99×56×40.图7给出了与场源中心距离为6 km的测点上所有频率的Ey分量和Bx分量的MFV数值解与解析解对比.从图中可以看出，所有频点的数值解与解析解均非常吻合.图8则给出了数值解相对于解析解的误差情况.从图中可以看出，当未进行场源校正时，大多数频点的电磁场分量的振幅误差为6%～8%；与之对比，采用场源校正技术后，电磁场分量的振幅误差降为5%以内.另外，在进行场源校正后，电磁场分量的相位误差略有增加，但仍保持在2°以内.在野外CSAMT测量中，由于各种人文噪声的影响，视电阻率误差和相位误差一般会比较大(Hu et al., 2013)，经过场源校正后，采用总场公式来进行CSAMT的正演模拟完全能够满足实测精度要求.

3.2三维模型的对比测试

在1D层状模型测试的基础上，本节对海洋3D模型进行了正演测试，并与已经发表的采用散射场公式的正演算法(韩波等, 2015b)所得到的结果进行了对比验证.

图9为典型海洋三维油气藏模型.油气藏模型尺寸为4 km×4 km×0.1 km，电阻率为100 Ωm，其顶部埋深距海底1000 m.均匀海底沉积层电阻率为1 Ωm，海水层厚度为1 km，电阻率为0.33 Ωm.观测系统设置为：发射偶极子沿x方向，位于海底上方100 m处，坐标为(0, 0, -100 m).接收站沿y=0的测线布设于海底，测线方向与偶极方向一致.发射频率为1 Hz.

图10给出了对于海洋三维模型，采用本文算法所得到的数值结果与散射场算法的正演结果对比图.从图中可以看出，无论是电场分量(图10a,b)还是磁场分量(图10c,d)，利用本文算法所得到的正演结果均与散射场算法的结果吻合的非常好，尽管在大偏移距处(>5 km)，两者的结果有略微的偏差.

3.3并行计算效率分析

为了检验本文所开发CSEM三维正演算法的并行效率，对陆地1D层状模型的多频率正演响应进行了并行计算测试，按对数等间隔在0.25～4096 Hz之间取12个频率.表1给出了使用不同数量的计算节点时的运行时间和并行加速比.可以看出，随着计算节点数的增加，总的计算时间迅速降低.由于各个频率之间的计算是完全独立的，主进程与各个子进程只涉及到非常少的通信(计算参数的分配及结果回收)，从并行加速比来看，并行效率非常接近于理想情况(加速比等于计算进程数).

程序运行模式计算节点数每个节点分配的频点个数模型剖分网格大小程序运行时间(s)并行加速比串行模式11299×56×405315.4无并行模式11299×56×405357.20.992699×56×402688.31.984399×56×401372.63.876299×56×40935.95.68

4　结论

(1) 本文采用直接解法来求解离散化的电场矢量Helmholtz方程，实现了基于有限体积法的频率域CSEM三维正演计算.对多个理论模型的正演测试结果表明本文的算法对于典型海洋和陆地CSEM测量是有效的.

(2) 由于采用直接解法来求解线性方程组，一次矩阵分解的结果可以用于不同发射源位置的计算，特别适合具有多发射源的CSEM测量；此外，在矩阵分解中，系数矩阵的病态程度对于矩阵分解结果影响很小，使得基于矩阵分解的直接解法对于包含强电性差异的地电模型都可以获得稳定且高精度的解.

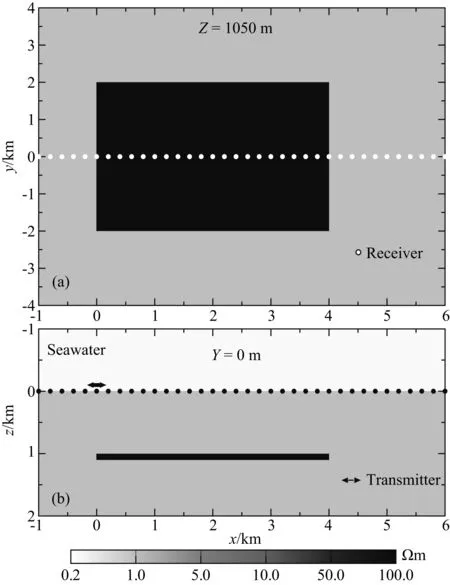
图9　海洋三维油气藏模型平面

图10　海洋三维模型数值结果对比(a)(c)电磁场分量振幅； (b)(d)电磁场分量相位.其中方框为本文正演所得到的结果，圆圈为韩波等(2015a)计算的结果.Fig.10　Comparison of data obtained from our modeling scheme to data resulted from Han et al. (2015a) for 3D marine model(a) Ex amplitudes； (b) Ex phases； (c) By amplitudes； (d) By phases.

(3) 采用了总场公式，场源的模拟采用直接离散化的方式.与基于散射场公式的正演算法相比，场源项的构建并不需要多次求解均匀模型或1D模型的一次电磁场，发射源位置的增加只引起计算量的少量增加，同样有利于多发射源的CSEM测量.与此同时，为避免对场源点附近进行网格局部加密所引起的计算量的增加，采用虚拟场源校正技术来降低场源奇异性及边界条件对数值精度的影响，取得了较好的效果.

(4) 三维电磁模拟对于计算资源要求很高，并且往往花费较长的计算时间.因此提高计算效率对于快速的电磁三维正反演至关重要.随着个人工作站和小型服务器的普及，一个有效的策略是考虑并行计算.对于多频率CSEM测量来说(如CSAMT)，基于分频并行的策略能够有效降低总的计算时间.另外，在计算资源允许的条件下，还可考虑对矩阵分解算法进行并行，从而进一步提高并行效率.

致谢感谢加拿大英属哥伦比亚大学(UBC)Eldad Haber教授的指导及与GIF组内同学进行的有益讨论，感谢MUMPS线性运算库的开发者们，感谢两名匿名审稿人对本文提出的宝贵修改意见.

Amestoy P R, Duff I S, L′Excellent J Y, et al. 2001. A fully asynchronous multifrontal solver using distributed dynamic scheduling.SIAMJournalonMatrixAnalysisandApplications, 23(1): 15-41. Amestoy P R, Guermouche A, L′Excellent J Y, et al. 2006. Hybrid scheduling for the parallel solution of linear systems.ParallelComputing, 32(2): 136-156.

Ansari S, Farquharson C G. 2014. 3D finite-element forward modeling of electromagnetic data using vector and scalar potentials and unstructured grids.Geophysics, 79(4): E149-E165.

Avdeev D, Knizhnik S. 2009. 3D integral equation modeling with a linear dependence on dimensions.Geophysics, 74(5): F89-F94.

Avdeev D B. 2005. Three-dimensional electromagnetic modelling and inversion from theory to application.SurveysinGeophysics, 26(6): 767-799.Avdeev D B, Kuvshinov A V, Pankratov O V, et al. 2002. Three-dimensional induction logging problems, Part I: An integral equation solution and model comparisons.Geophysics, 67(2): 413-426.

Badea E A, Everett M E, Newman G A, et al. 2001. Finite-element analysis of controlled-source electromagnetic induction using Coulomb-gauged potentials.Geophysics, 66(3): 786-799.

Börner R U. 2010. Numerical modelling in geo-electromagnetics: advances and challenges.SurveysinGeophysics, 31(2): 225-245.

Chung Y, Son J S, Lee T J, et al. 2014. Three-dimensional modelling of controlled-source electromagnetic surveys using an edge finite-element method with a direct solver.GeophysicalProspecting, 62(6): 1468-1483.

Di Q Y, Wang R. 2008. Controlled Source Audio-Frequency Magneto Tellurics (in Chinese). Beijing: Science Press.

Grayver A V, Streich R, Ritter O. 2013. Three-dimensional parallel distributed inversion of CSEM data using a direct forward solver.GeophysicalJournalInternational, 193(3): 1432-1446.

Haber E, Ascher U M. 2001. Fast finite volume simulation of 3D electromagnetic problems with highly discontinuous coefficients.SIAMJournalonScientificComputing, 22(6): 1943-1961. Haber E, Heldmann S. 2007. An octree multigrid method for quasi-static Maxwell′s equations with highly discontinuous coefficients.JournalofComputationalPhysics, 223(2): 783-796. Haber E, Ruthotto L. 2014. A multiscale finite volume method for Maxwell′s equations at low frequencies.GeophysicalJournalInternational, 199(2): 1268-1277.

Han B, Hu X Y, Huang Y F, et al. 2015b. 3-D frequency-domain CSEM modeling using a parallel direct solver.ChineseJ.Geophysics(in Chinese), 58(8): 2812-2826, doi: 10.6038/cjg20150816.

Han B, Hu X Y, Schultz A, et al. 2015a. Three-dimensional forward modeling of the marine controlled-source electromagnetic field with complex source geometries.ChineseJ.Geophys. (in Chinese), 58(3): 1059-1071, doi: 10.6038/cjg20150330.Hu X Y, Peng R H, Wu G J, et al. 2013. Mineral exploration using CSAMT data: Application to Longmen region metallogenic belt, Guangdong Province, China.Geophysics, 78(3): B111-B119.

Huang Q H, Li Z H, Wang Y B. 2010. A parallel 3-D staggered grid pseudospectral time domain method for ground-penetrating radar wave simulation.JournalofGeophysicalResearch, 115(B12): B12101, doi: 10.1029/2010JB007711.

Hursán G, Zhdanov M S. 2002. Contraction integral equation method in three-dimensional electromagnetic modeling.RadioScience, 37(6): 1-1-1-13.

Hyman J, Shashkov M, Steinberg S. 1997. The numerical solution of diffusion problems in strongly heterogeneous non-isotropic materials.JournalofComputationalPhysics, 132(1): 130-148.

Hyman J M, Shashkov M. 1997. Adjoint operators for the natural discretizations of the divergence, gradient and curl on logically rectangular grids.AppliedNumericalMathematics, 25(4): 413-442.

Hyman J M, Shashkov M. 1999a. Mimetic discretizations for Maxwell′s equations.JournalofComputationalPhysics, 151(2): 881-909.

Hyman J M, Shashkov M. 1999b. The orthogonal decomposition theorems for mimetic finite difference methods.SIAMJournalonNumericalAnalysis, 36(3): 788-818.

Jahandari H, Farquharson C G. 2014. A finite-volume solution to the geophysical electromagnetic forward problem using unstructured grids.Geophysics, 79(6): E287-E302.

Key K. 2009. 1D inversion of multicomponent, multifrequency marine CSEM data: Methodology and synthetic studies for resolving thin resistive layers.Geophysics, 74(2): F9-F20.

Knizhnerman L, Druskin V, Zaslavsky M. 2009. On optimal convergence rate of the rational Krylov subspace reduction for electromagnetic problems in unbounded domains.SIAMJournalonNumericalAnalysis, 47(2): 953-971. Li X S. 2005. An overview of SuperLU: Algorithms, implementation, and user interface.ACMTransactionsonMathematicalSoftware(TOMS), 31(3): 302-325.

Li Y, Wu X P, Lin P R. 2015. Three-dimensional controlled source electromagnetic finite element simulation using the secondary field for continuous variation of electrical conductivity within each block.ChineseJ.Geophys. (in Chinese), 58(3): 1072-1087, doi: 10.6038/cjg20150331.

Liu L B, Li Z H, Arcone S, et al. 2013. Radar wave scattering loss in a densely packed discrete random medium: Numerical modeling of a box-of-boulders experiment in the Mie regime.JournalofAppliedGeophysics, 99: 68-75, doi: 10.1016/j.jappgeo.2013.08.022.

Mackie R L, Smith J T, Madden T R. 1994. Three-dimensional electromagnetic modeling using finite difference equations: the magnetotelluric example.RadioScience, 29(4): 923-935.

Newman G A, Alumbaugh D L. 1995. Frequency-domain modelling of airborne electromagnetic responses using staggered finite differences.GeophysicalProspecting, 43(8): 1021-1042.

Oldenburg D W, Haber E, Shekhtman R. 2013. Three dimensional inversion of multisource time domain electromagnetic data.Geophysics, 78(1): E47-E57.

Pardo D, Paszynski M, Collier N, et al. 2012. A survey on direct solvers for Galerkin methods.SEMAJournal, 57(1): 107-134.

Pidlisecky A, Haber E, Knight R. 2007. RESINVM3D: A 3D resistivity inversion package.Geophysics, 72(2): H1-H10.

Pidlisecky A, Knight R. 2008. FW2_5D: A MATLAB 2.5-D electrical resistivity modeling code.Computer&Geosciences, 34(12): 1645-1654.

Plessix R E, Darnet M, Mulder W A. 2007. An approach for 3D multisource, multifrequency CSEM modeling.Geophysics, 72(5): SM177-SM184.

Puzyrev V, Koldan J, de la Puente J, et al. 2013. A parallel finite-element method for three-dimensional controlled-source electromagnetic forward modelling.GeophysicalJournalInternational, 193(2): 678-693. Qiu Z P, Li Z H, Li D Z, et al. 2013. Non-orthogonal-Grid-based three dimensional modeling of transient electromagnetic field with topography.ChineseJ.Geophys. (in Chinese), 56(12): 4245-4255, doi: 10.6038/cjg20131227.

Schenk O, G?rtner K. 2006. On fast factorization pivoting methods for sparse symmetric indefinite systems.ElectronicTransactionsonNumericalAnalysis, 23(1): 158-179.

Schwarzbach C, B?rner R U, Spitzer K. 2011. Three-dimensional adaptive higher order finite element simulation for geo-electromagnetics—a marine CSEM example.GeophysicalJournalInternational, 187(1): 63-74.

Shen J S. 2003. Modeling of 3-D electromagnetic responses in frequency domain by using staggered-grid finite difference method.ChineseJ.Geophys. (in Chinese), 46(2): 281-288.

Smith J T. 1996. Conservative modeling of 3-D electromagnetic fields, Part I: Properties and error analysis.Geophysics, 61(5): 1308-1318.

Streich R. 2009. 3D finite-difference frequency-domain modeling of controlled-source electromagnetic data: Direct solution and optimization for high accuracy.Geophysics, 74(5): F95-F105.

Streich R, Becken M, Matzander U, et al. 2011. Strategies for land-based controlled-source electromagnetic surveying in high-noise regions.TheLeadingEdge, 30(10): 1174-1181.

Ward S H, Hohmann G W. 1988. Electromagnetic theory for geophysical applications.∥ Electromagnetic Methods in Applied Geophysics: Vol. I, Theory. Tulsa, OK: SEG. Weiss C J, Constable S. 2006. Mapping thin resistors and hydrocarbons with marine EM methods, Part II: Modeling and analysis in 3D.Geophysics, 71(6): G321-G332. Weiss C J, Newman G A. 2002. Electromagnetic induction in a fully 3-D anisotropic earth.Geophysics, 67(4): 1104-1114.

Xu Z F, Wu X P. 2010. Controlled source electromagnetic 3-D modeling in frequency domain by finite element method.ChineseJ.Geophys. (in Chinese), 53(8): 1931-1939, doi: 10.3969/j.issn.0001-5733.2010.08.019. Yang B, Xu Y X, He Z X, et al. 2012. 3D frequency-domain modeling

of marine controlled source electromagnetic responses with topography using finite volume method.ChineseJ.Geophys. (in Chinese), 55(4): 1390-1399, doi: 10.6038/j.issn.0001-5733.2012.04.035.

Yang J, Liu Y, Wu X P. 2015. 3D simulation of marine CSEM using vector finite element method on unstructured grids.ChineseJ.Geophys. (in Chinese), 58(8): 2827-2838, doi: 10.6038/cjg20150817.

Yee K S. 1966. Numerical solution of initial boundary value problems involving Maxwell′s equations in isotropic media.IEEETransactionsonAntennasandPropagation, 14(3): 302-307.

Zhdanov M S, Lee S K, Yoshioka K. 2006. Integral equation method for 3D modeling of electromagnetic fields in complex structures with inhomogeneous background conductivity.Geophysics, 71(6): G333-G345.

Zhdanov M S, Masashi E, Cox L H, et al. 2014. Three-dimensional inversion of towed streamer electromagnetic data.GeophysicalProspecting, 62(3): 552-572.

附中文参考文献

底青云, 王若. 2008. 可控源音频大地电磁数据正反演及方法应用. 北京: 科学出版社.

韩波, 胡祥云, 黄一凡等. 2015b. 基于并行化直接解法的频率域可控源电磁三维正演. 地球物理学报, 58(8): 2812-2826, doi: 10.6038/cjg20150816.

韩波, 胡祥云, Schultz A等. 2015a. 复杂场源形态的海洋可控源电磁三维正演. 地球物理学报, 58(3): 1059-1071, doi: 10.6038/cjg20150330.

李勇, 吴小平, 林品荣. 2015. 基于二次场电导率分块连续变化的三维可控源电磁有限元数值模拟. 地球物理学报, 58(3): 1072-1087, doi: 10.6038/cjg20150331.

邱稚鹏, 李展辉, 李墩柱等. 2013. 基于非正交网格的带地形三维瞬变电磁场模拟. 地球物理学报, 56(12): 4245-4255, doi: 10.6038/cjg20131227.

沈金松. 2003. 用交错网格有限差分法计算三维频率域电磁响应. 地球物理学报, 46(2): 281-288.

徐志锋, 吴小平. 2010. 可控源电磁三维频率域有限元模拟. 地球物理学报, 53(8): 1931-1939, doi: 10.3969/j.issn.0001-5733.2010.08.019.

杨波, 徐义贤, 何展翔等. 2012. 考虑海底地形的三维频率域可控源电磁响应有限体积法模拟. 地球物理学报, 55(4): 1390-1399, doi: 10.6038/j.issn.0001-5733.2012.04.035.

杨军, 刘颖, 吴小平. 2015. 海洋可控源电磁三维非结构矢量有限元数值模拟. 地球物理学报, 58(8): 2827-2838, doi: 10.6038/cjg20150817.

(本文编辑张正峰)

3D frequency-domain CSEM forward modeling based on the mimetic finite-volume method

PENG Rong-Hua1,2, HU Xiang-Yun1*, HAN Bo3, CAI Jian-Chao1

1InstituteofGeophysicsandGeomatics,ChinaUniversityofGeosciences,Wuhan430074,China2DepartmentofEarth,OceanandAtmosphericSciences,UniversityofBritishColumbia,VancouverV6T1Z4,Canada3CollegeofMarineGeosciences,OceanUniversityofChina,Qingdao266100,China

Quantitative interpretation of large-scale controlled-source electromagnetic (CSEM) data in the frequency domain requires efficient and stable three-dimensional (3D) forward modeling and inversion codes. In this paper, we present a 3D forward modeling scheme for frequency-domain CSEM surveys based on the mimetic finite volume (MFV) method, which solves the Helmholtz equation for the total electric field.

Controlled-source electromagnetic； Mimetic finite volume method； 3D forward modeling； Source correction technique； Direct solver

10.6038/cjg20161036.

国家自然科学基金(41274077和41474055)、国家重点基础研究发展计划项目(2013CB733200)、国家留学基金委(201406410020)和湖北省自然科学基金(2015CFA019)联合资助.

彭荣华，男，1988年生，博士研究生，研究方向为电磁法三维正演与反演模拟.E-mail:prhjiajie@163.com

胡祥云，男，1966年生，教授，博士生导师，主要从事电磁法的理论与应用研究.E-mail：xyhu@cug.edu.cn

10.6038/cjg20161036

P631

2016-07-06，2016-09-12收修定稿

彭荣华， 胡祥云， 韩波等. 2016. 基于拟态有限体积法的频率域可控源三维正演计算. 地球物理学报，59(10):3927-3939,

Peng R H, Hu X Y, Han B, et al. 2016. 3D frequency-domain CSEM forward modeling based on the mimetic finite-volume method.ChineseJ.Geophys. (in Chinese),59(10):3927-3939,doi:10.6038/cjg20161036.