基于CHAMP、GRACE和COSMIC掩星数据的全球电离层hmF2建模研究

刘桢迪， 方涵先*， 翁利斌， 马强， 张建彬

1 解放军理工大学气象海洋学院， 南京　211101 2 中国人民解放军63655部队， 乌鲁木齐　841700



基于CHAMP、GRACE和COSMIC掩星数据的全球电离层hmF2建模研究

刘桢迪1， 方涵先1*， 翁利斌1， 马强1， 张建彬2

1 解放军理工大学气象海洋学院， 南京211101 2 中国人民解放军63655部队， 乌鲁木齐841700

基于CHAMP、GRACE和COSMIC的电离层hmF2掩星数据，采用最小二乘法建立了一个包含地磁和太阳活动、经度、地方时、年积日和纬度信息的非线性多项式hmF2模型(Nonlinear Polynomial Peak Height Model—NPPHM).利用GRACE掩星数据对NPPHM与IRI2012进行了独立检验，结果显示这两个模型在2008年与GRACE数据的相关系数分别为0.798和0.532，均方根误差分别为25.97 km和44.56 km；在2012年，相关系数分别为0.732和0.488，均方根误差分别为31.39 km和42.83 km.选取全球不同地区14个测高仪站点数据，并引入相似离度对这两个模型的精度进行了评估，结果表明，NPPHM的相似离度远小于IRI2012，更加接近测高仪观测值.使用Athens站2003—2013年数据对模型进行了检验，结果显示IRI2012与Athens站测高仪数据的平均偏差达到8.11%，NPPHM则只有3.53%，并且在太阳活动低年及每年10月NPPHM的精度要明显高于IRI2012.此外，NPPHM也能够较好模拟出hmF2的日变化、季节变化及赤道异常等特性.

电离层hmF2建模；非线性多项式；掩星数据

1　引言

电离层F2层的电子密度峰值高度(hmF2)是电离层物理中一个十分重要的参量.它对高频电波在电离层内的传播和反射具有重要影响.hmF2的抬升或下降将直接影响到信号在电离层内的传播，可能改变其传输路径，造成信号中断.因此，对hmF2的研究将有助于无线电波频谱管理.在构建电离层电子密度剖面时，hmF2是其中一个至关重要的因素.所以，对峰值高度hmF2的建模具有重要的科学意义.

电离层hmF2存在较为复杂的变化，它在赤道地区的分布范围一般是350～500 km，在中纬地区一般是250～350 km.hmF2也存在依赖于季节、地方时、太阳活动和地磁活动的变化特性.此外，电场漂移及中性风等对hmF2也具有一定的调制作用(Hoque and Jakowski，2012).

目前，国际参考电离层模型IRI是应用广泛的hmF2经验模型.IRI模型是根据大量电离层探测数据得到的经验预报模型，它综合了全球180多个数字测高仪站点的资料，主要描述了海拔高度50～1500 km范围内平静地磁场条件下非极区电离层的峰值高度、电子密度、电子温度、离子成分、离子温度和离子漂移的月平均值等重要参数(Bilitza et al., 1979).继Rawer(1978)发布了第一个版本的IRI之后，学者们又提出了多个IRI的更新版本(Bilitza et al., 1979; Bilitza, 1990, 2015; Bilitza and Reinisch, 2008)，目前国际参考电离层的最新版本为IRI2012.IRI利用F2层传输因子M(3000)F2参量来得到hmF2，二者的转换方程只有在近似假设电子密度与高度呈抛物型相关的条件下才能成立(Shubin et al., 2013)，但这一假设与实际情况并不完全相符.Magdaleno 等(2011)的研究表明，在高纬地区IRI模型值超出测高仪实测值的30%左右，在赤道附近则低估达40%左右.

近来，很多学者利用不同的观测数据和方法对hmF2的建模进行了研究.例如，Zhang等(2009，2010)使用经验正交函数(EOF)、Altadill等(2013)使用球谐函数构造了全球hmF2经验模型，Brunini等(2013)则分别使用不同的数学表达来描述hmF2的全球变化和日变化.但是，这些模型都是基于地基测高仪数据建立的.虽然地面测站已经积累了较长时间的电离层观测数据，但全球站点的数量极为有限，且全球分布不均(在海洋上几乎没有分布)，这是以上建模的不足之处.随着掩星技术的发展，研究人员基于掩星数据也构建了一些hmF2模型，例如Shubin等(2013)使用勒让德函数和傅里叶展开分别描述hmF2的空间变化和时间变化，得到了SMF2(the Satellite Model of the F2layer)模型，但是，SMF2模型缺少太阳活动变化项，只能局限于太阳活动低年使用.Hoque和Jakowski(2012)利用非线性多项式方程，建立了hmF2的NPHM(Neustrelitz Peak Height Model)模型.然而，NPHM模型只包含13个系数，并且模型缺少经度变化项和地磁变化项，它与NeQuick模型(Radicella and Leitinger，2001)的比较表明两者的相对误差是接近的，可见NPHM在精度上提高不大.

本文利用CHAMP(Challenging Minisatellite Payload), GRACE(Gravity Recovery And Climate Experiment)和COSMIC(Constellation Observing System for Meteorology, Ionosphere and Climate)的掩星探测数据，基于目前对电离层hmF2的研究基础，使用非线性多项式方程对全球hmF2建模.利用非线性多项式方程能够构建出形式相对简单、计算效率相对较快，同时精度较高的模型(Hoque and Jakowski, 2012).同NPHM模型相比，本文采用的非线性多项式包含315个系数，且除纬度、太阳活动、年积日和地方时外，更为全面的考虑了经度和地磁活动两项影响因素.此外，本文将全球按照纬度划分为71个纬度带，在各纬度带内分别通过最小二乘拟合确定系数，从而回避了在模型中加入先验纬度变化信息，进一步提高模型的计算效率和准确性.使用GRACE数据、地面测高仪数据对模型进行了独立检验，并利用NPPHM模拟了hmF2变化特性，评估NPPHM的精度和模拟能力.

2　数据

本文使用了掩星数据进行建模和检验，这部分数据源由CHAMP卫星2001年6月到2008年9月、GRACE卫星2007年2月到2013年9月和COSMIC卫星2006年4月到2014年12月的掩星剖面(EDP)组成.Hajj和Romans(1998)、Garcia-Fernandez 等(2003)和Lei等(2007)对掩星反演技术做出了详细说明.通过Abel变换可以从掩星观测中获得十分准确的F2层峰值高度(hmF2)和峰值密度(NmF2).Yue等(2010)指出反演得到的hmF2与真实值之间的绝对标准差为8.9 km(夜间)和7.4 km(白天)，相对标准差为2%(夜间)和2%(白天).Lei 等 (2007)将掩星反演得到的hmF2与Millstone Hill站的非相干散射雷达观测数据及Jicamarca站的垂测仪观测数据进行比较后发现，掩星反演的偏差范围为10～30 km.Krankowski等(2011)利用部分欧洲垂测仪数据对掩星反演的hmF2做了进一步研究发现，两种数据的平均偏差为2.8 km.CHAMP和GRACE卫星的掩星剖面由German Aerospace Center(DLR)Neustrelitz(http:∥swaciweb.dlr.de/)提供.COSMIC掩星剖面由COSMIC Data Analysis and Archive Center(CDAAC,http:∥cosmic-io.cosmic. ucar.edu/cdaac/index. html)提供.从掩星剖面中，可以获取各个高度处的电子密度及精度较高的地理坐标.对于得到的剖面，根据Lei等(2007)的研究，本文筛选出，150 km≤hmF2≤600 km，103·cm-3≤NmF2≤8×106·cm-3，并且卫星轨道高度(orbalt)满足orbalt≥hmF2+50的剖面，从中提取出对应的hmF2.最终由COSMIC得到有效数据约3.8×106个(约占总数据的92%)，由CHAMP得到有效数据约2.2×105个(约占总数据的5%)，由GRACE得到有效数据约1.3×105个(约占总数据的3%).图1表示选用数据随太阳活动水平、地理纬度、地理经度、年积日、地方时和地磁指数的分布情况.从图1可知，建模所用数据对经度、年积日和地方时的覆盖较为全面和均匀；中低纬数据较多，高纬数据较少；低太阳活动水平分布较多，高太阳活动水平分布较少，F10.7>150时分布极少；地磁活动弱时的数据较多，地磁活动强时的数据较少，Ap>20的数据极少.

图1　数据随太阳活动、年积日、地理纬度、地方时、地理经度、地磁指数的分布情况Fig.1　Data distributions as F10.7, day of year, Geographical Latitude, Local Time，Geographical Longitude and geomagnetic index Ap

另外，本文也使用了地基测高仪hmF2数据进行检验.这部分数据由Space Physics Interactive Data Resource (SPIDR,http:∥spidr.ngdc.noaa.gov/spidr/)提供.我们选取了14个能够代表全球不同区域的测站.由于测高仪数据只用于对模型的检验，所以具体的测站坐标及数据内容将在第4节予以说明.

3　方法和结果

3.1建模方法

采用非线性多项式方程对全球hmF2建模.非线性多项式方程已经被成功应用到顶部电离层标高模型、电离层电子总含量模型及热层大气密度模型等多个经验模型中(Kutiev et al., 2006;Kakinami et al., 2008,2009; Liu et al., 2013).

为提高计算效率，同时避免在模型中加入先验纬度变化信息，本文采用划分纬度带分别建模的方法.将全球hmF2数据从90°S开始向北按照地理纬度间隔5°进行划分.同时，为避免模型出现纬度变化不光滑的情况，使相邻纬度带之间重合2.5°的区域，最终将全球划分为71个纬度带.在各纬度带内分别拟合求相应的系数.每个纬度带的中间纬度作为该纬度带拟合所得系数对应的纬度，其他纬度处的系数可以通过插值得到.表1给出了前5个纬度带的具体情况.

表1　前5个纬度带范围及所得系数对应的纬度Table 1　Ranges of the first 5 latitude zones and the corresponding latitude for each group of coefficients

除纬度外，影响hmF2的因素主要包括地理经度(Lon)、太阳活动(F10.7)、地磁活动(Ap)、地方时(LT)和年积日(Doy).非线性多项式模型是基于这些影响因素都是相互独立的假定建立的.但是在研究中我们发现，将太阳活动、地磁活动和地理经度作为独立项时，模型精度并没有得到明显提高，然而计算效率却大大下降，所以本文将这三项因素作为一个独立多项式加以考虑，这与Liu等(2013)的处理方法相似.具体模型形式如下：

hmF2=F1(F10.7,Ap,Lon)F2(LT)F3(Doy),

(1)

方程(1)中F1-3是分别表示各项变化且含有多个系数的多项式.F1表征hmF2随太阳活动(F10.7)、地磁指数(Ap)和地理经度(Lon)的变化.根据Liu 等 (2005) 和Müller 等 (2009) 的研究，地磁活动项取为线性关系.Shubin (2015)指出太阳活动与hmF2之间近似为对数关系.所以F1具体形式如下：

(2)

F1含有(2M+3)个系数.

F2表征hmF2随地方时(LT)的日变化：

(3)

F2含有(2N+1)个系数.

F3表征hmF2随年积日(Doy)的季节变化：

(4)

F3含有(2P+1)个系数.

需要注意的是，利用最小二乘原理进行拟合确定系数时，先根据方程(2)—(4)将(1)式展开.方程(2)—(4)相乘后总共得到[(2M+3)×(2N+1)×(2P+1)]个独立系数.与Hoque和Jakowski(2012)的方法相似，方程(3)中，取N=3，分别表示hmF2的日变化、半日变化和1/3日变化；根据Lin等(2014)的研究，方程(4)中，取P=2，分别表示hmF2的年变化和半年变化.为获取较高的精度，同时提高模型计算效率，本文对方程(1)中M的不同取值进行了研究对比，最终选取M=3.模型在全球的71个纬度带内共有9×7×5×71=22365个系数，它们由掩星数据通过最小二乘法拟合得到.

3.2建模结果

为了检验拟合效果，需要对NPPHM的残差进行分析.根据建模使用的掩星数据源对应的纬度、经度、年积日、地方时、太阳活动和地磁活动，得到NPPHM及IRI2012对应的模型值(mod)，计算模型值与原始数据(obs)间的相对偏差(RD)、平均相对偏差(Mean)和均方差(STD)：

(5)

(6)

(7)

(8)

图2给出了NPPHM和IRI2012相对偏差的统计结果，实线是NPPHM的统计结果，虚线是IRI2012的统计结果.IRI2012相对偏差偏向正值区分布且在偏差较大区域分布较多，平均相对偏差达7.3%，均方差为14.99%.而NPPHM偏差呈现正态分布特征，大部分集中在0附近，向正负两侧迅速减少，平均相对偏差为0.81%，均方差为9.57%.由此可见，建模的结果是比较理想的.

4　模型检验

利用建模数据源以外的掩星数据和电离层测高仪数据，对模型进行独立检验，并同时与IRI2012的精度进行对比.此外，利用NPPHM模拟hmF2的形态特征以检验其表征hmF2变化特性的性能.

图2　相对偏差分布直方图Fig.2　Histogram of relative deviation

4.1GRACE掩星数据独立检验

分别选取GRACE 2008年和2012年的掩星数据，与NPPHM和IRI2012进行比对.需要指出的是，这一步进行检验的模型，是将2008年和2012年GRACE掩星数据分别从建模原始数据源中剔除后重新建模所得到的结果，所以验证数据是独立的.2008年和2012年分别是太阳活动低年和较高年.此外，这些数据涵盖了大量不同的经纬度、地方时和年积日.图3和图4分别是2008年和2012年的比对结果，同时计算给出了相关系数(R)、平均相对偏差(Mean)和均方根误差(RMS).均方根误差(RMS)计算方法如下：

(9)

由图3可以看出，2008年太阳活动低年期间，NPPHM与GRACE掩星观测值的相关系数为0.798，高于IRI2012的0.532；两个模型的平均相对偏差分别为1.93%和11.48%，表明NPPHM的偏差远小于IRI2012；均方根误差分别为25.97 km和44.56 km，NPPHM比IRI2012降低了约42%.

图3　2008年NPPHM与IRI2012 hmF2同GRACE hmF2的散点分布图Fig.3　Scatter plots of NPPHM results and IRI2012 results versus GRACE hmF2 in 2008

图4所示的2012年是太阳活动水平较高年份，NPPHM和IRI2012与观测值的相关系数分别为0.732和0.488，前者较后者提高了约50%；平均相对偏差分别为0.19%和5.97%；均方根误差分别为31.39 km和42.83 km，前者较后者降低了约27%.

从GRACE掩星数据的检验结果来看，IRI2012经验模式与掩星观测数据相比存在较大的偏差，而NPPHM模型的偏差较小，尤其在太阳活动低年，NPPHM的偏差进一步减小，这可能是因为建模使用的原始数据大部分集中在太阳活动低年，高年数据较少.需要指出的是，当电离层受到磁暴等异常活动影响时，峰值高度hmF2可能会出现极高或极低值，然而这部分的数据量很少且电离层暴变化非常复杂，所以NPPHM与IRI2012模型均在这些情况下出现了较大的偏差，这是经验模型的建模原理所决定的.

4.2电离层测高仪数据检验

4.2.1全球hmF2分布检验

选取代表全球不同区域的电离层测高仪数据，与NPPHM和IRI2012进行比对.分别选取了南、北半球各4个测站的3、6、9和12月的数据，分别代表了春、夏、秋、冬四个季节.这些测站代表着南北半球的低、中、高纬地区及东西半球的美洲、欧洲和大洋洲地区，表2列出了选取测站的地理坐标.为了保证测站当月的hmF2数据量足够多，选取数据的时间段范围较宽，包括2007年、2008年、2013年和2014年.其中2007年和2008年是太阳活动低年，2013年和2014年是太阳活动高年.图5表示上述4年F10.7指数随年积日的变化.

将测高仪hmF2的月均值(Ionosonde)与NPPHM及IRI2012的模型月均值进行比较.为了全面评估模型值与观测值在变化趋势及数值大小上的一致程度，本文引入相似离度进行分析.相似离度不仅能够体现样本间数值差异的大小，而且能够体现样本间形态上的相似，是一种比较全面的相似衡量标准(李开乐，1986；翁利斌等，2011)，它在气象相关领域得到了广泛应用.计算公式为

图4　2012年NPPHM与IRI2012hmF2同GRACE hmF2的散点分布图Fig.4　Scatter plots of NPPHM results and IRI2012 results versus GRACE hmF2 in 2012

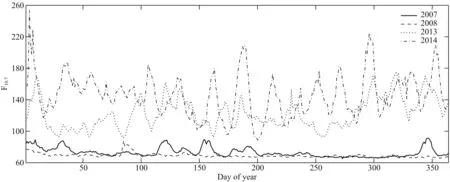
图5　2007年、2008年、2013年和2014年太阳活动变化Fig.5　The variations of F10.7 in 2007,2008,2013 and 2014

站点纬度/°N经度/°E站点纬度/°N经度/°EKwajalein9167.2Jicamarca-12.1-77PuertoRico18.5-67.2Madimbo-22.430.9Athens3823.5Louisvale-28.521.2Boulder40-105.3Hermanus-34.419.2MillstoneHill42.6-71.5Bundoora-37.72145.05Moscow55.537.3PortStanley-51.7-57.8College64.9-147.8Thule77.5-69.2

(10)

其中，

(11)

(12)

(13)

(14)

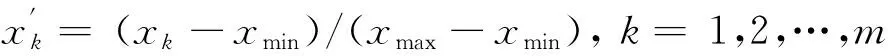
图6给出了太阳活动低年的分析结果，图7给出了太阳活动高年的分析结果.从图6可以看出，在太阳活动低年，IRI2012普遍偏高，而NPPHM在南北半球的春、夏、秋、冬四个季节都与测高仪观测值更加接近.NPPHM在反映hmF2的变化趋势上也优于IRI2012.例如Boulder站LT=23时左右测高仪观测数据显示出上升趋势，NPPHM呈现出相同的趋势，而IRI2012则出现了下降趋势；Madimbo站LT=12时左右观测数据出现下降，但这一变化十分微小且持续时间很短，可以忽略，NPPHM保持水平，而IRI2012则出现较为明显的上升趋势.从相似离度的分析可以看出，NPPHM与观测值的相似离度均小于IRI2012，且有较大提升.例如在Kwajalein站，IRI2012的相似离度是0.285，NPPHM的相似离度是0.156，提升45%以上.

图6　太阳活动低年测高仪(点)、NPPHM(实线)和IRI2012(虚线)hmF2月均值随地方时的变化情况上四幅表示北半球，下四幅表示南半球；从左至右分别表示3月、6月、9月和12月；c1、c2分别表示IRI2012和NPPHM同测高仪的相似离度.Fig.6　Variations of monthly mean of NPPHM (solid lines) and IRI2012 (dotted lines) as a function of LT in comparisons with ionosonde observation (dots) in low solar activity yearsThe upper panel is the Northern Hemisphere, the lower panel is the Southern Hemisphere; fromleft to right is March, June, September and December, respectively; c1 is the analog deviation between IRI2012 and ionosonde observation, c2 is the analog deviation between NPPHM and ionosonde observation.

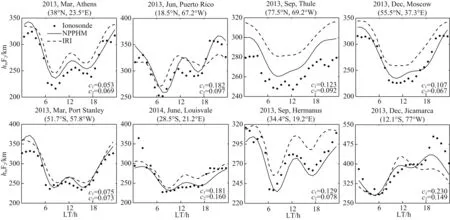
图7　同图6，太阳活动高年情况Fig.7　Same as Fig.6,but for high solar activity years

由图7可知，在太阳活动高年，NPPHM相比于IRI2012更接近实测值.从相似离度的分析结果可以看出，在其中7个测站NPPHM的相似离度小于IRI2012.例如，在Puerto Rico站，IRI2012相似离度为0.182，而NPPHM的相似离度为0.097，提升47%左右.但是，在Athens站，NPPHM的相似离度略高于IRI2012，分别为0.069和0.053，这可能是太阳活动高年的建模数据较少造成的.

总体来看，不论在太阳活动低年还是太阳活动高年，NPPHM在绝大部分测站处的精度优于IRI2012，在数值和形态上都与测高仪观测值更加相似.同时我们也注意到，从全球来看，NPPHM在低纬赤道地区的相似离度较其他地区偏高，这可能是由于低纬赤道地区不满足掩星数据反演过程中的球对称假设，因此产生了一定的反演误差.下一步我们将引入包括低纬赤道地区在内的垂测仪hmF2数据，以进一步改进NPPHM的区域适用性.

4.2.2长期hmF2变化检验

选取Athens站(38°N，23.5°E)一个太阳活动周(2003—2013年)的观测数据，对11年数据逐月(Month)逐世界时(UT)求出hmF2的月均值，以检验NPPHM在一个完整的太阳活动周内的表现.图8给出了11年间月均值的变化情况.图8(中)出现的空缺部分是因为Athens站缺少2008年8月、9月、10月和2012年6月所有时刻的数据以及2012年7月部分时刻的数据.

由图8可知，NPPHM能够较为准确地反映出11年间Athens站的月均值变化，高低值分布及变化趋势都与测高仪数据比较一致.经计算，2003—2013年IRI2012与Athens站测高仪数据的平均偏差(Mean)达到8.11%，NPPHM则只有3.53%，后者比前者降低了约56.5%.注意到，IRI2012在每年10月的UT=9—12时之间出现明显的高值区，而测高仪数据则相应的表现为低值区，NPPHM与测高仪数据表现一致.表3分别列出了各年10月UT=9、10、11、12时的月均值偏差.由表3可知，NPPHM的偏差在0附近波动，有正有负，其绝对值绝大部分在20 km以下，最高为28.79 km；而IRI2012的偏差全部为正值，大部分在50 km以上，最高达83.37 km.2006—2010年间，测高仪数据在UT=6—18时较低，大部分在200 km以下，最低达180 km；在UT=0—5时及UT=19—23时之间较高，但大部分也在280 km以下，最高达300 km.NPPHM与测高仪观测值相似，而IRI2012则明显偏高，在UT=6—18时之间普遍偏高20 km以上，且出现了300 km左右的高值，在UT=0—5时及UT=19—23时之间，hmF2大多数分布在300～330 km之间.表4列出了2006—2010年间NPPHM和IRI2012在UT=19—23时之间的平均偏差.从表4可以看出，NPPHM的平均偏差绝对值均在2 km以下，而IRI2012均在25 km以上.

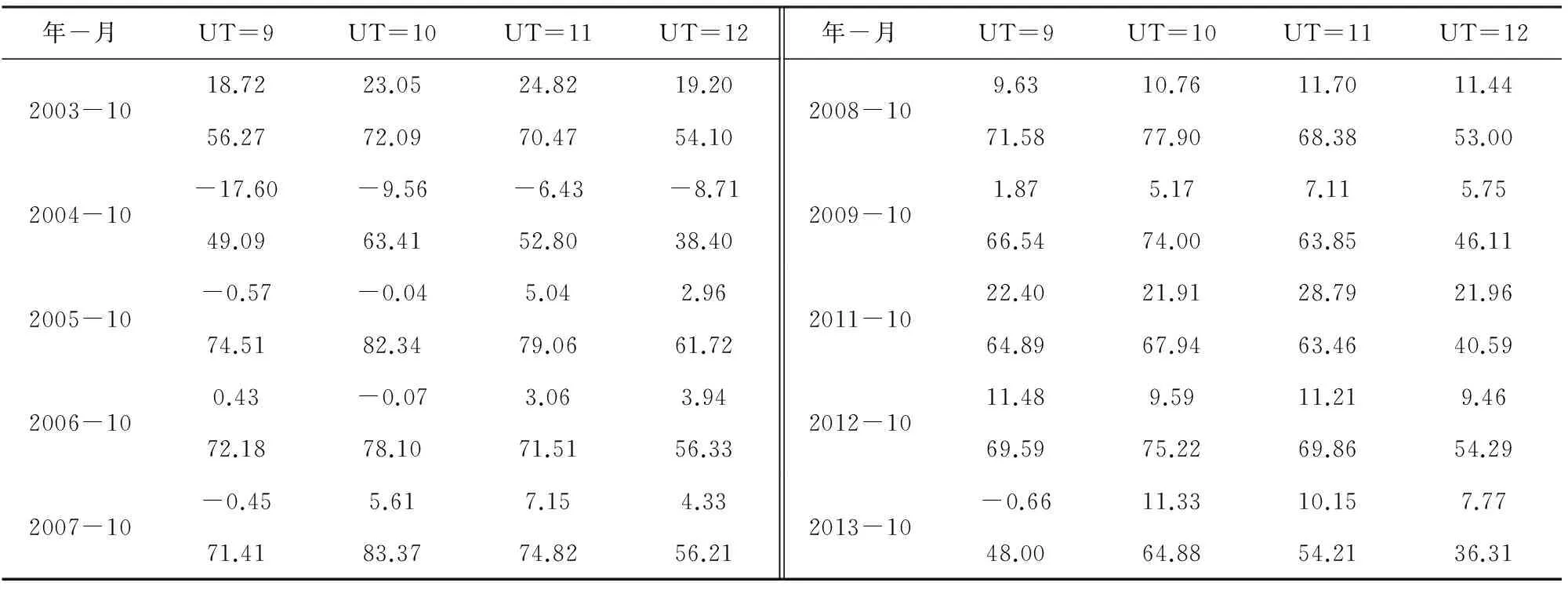
表3　UT=9、10、11、12时的月均值偏差(单位：km)Table 3　The deviation of monthly mean at UT=9,10,11,12 (unit: km)

注：每个月的上一行表示NPPHM偏差，下一行表示IRI2012偏差.

表4　UT=19—23之间的平均偏差Table 4　Mean deviation from UT=19 to UT=23

4.3hmF2变化特性检验

为了检验NPPHM表征hmF2随纬度(Lat)、地方时(LT)和年积日(Doy)变化的性能，本文研究了NPPHM在确定经度(Lon)、太阳活动(F10.7)和地磁指数(Ap)条件下的模型结果.当Lon=70°W，Ap=5时，图9(a1—a4)分别给出了F10.7=80条件下春分日(Doy=80)、夏至日(Doy=173)、秋分日(Doy=266)和冬至日(Doy=356)的hmF2分布情况;图9(b1—b4)给出了F10.7=120条件下相同年积日的分布情况.从图9可知，白天hmF2在磁赤道附近显著增强，这与我们熟知的电离层赤道异常现象相符，并且由图9可知这种异常在LT=12时和LT=20时左右出现两个峰值，这与Yue 等(2015)的研究结果一致.LT=12时的增强是由于此时太阳天顶角最小，太阳辐射最强，热层大气电离产生的等离子体在电场作用下向上漂移；LT=20时的增强是日落期间向上垂直漂移的反转增强造成的.由图9分析hmF2的日变化可知，磁赤道附近白天hmF2高于夜间，中纬及高纬地区夜间hmF2高于白天，这与我们已知的结论是相符的(熊年禄等，1999).造成这种现象的原因是在中高纬地区，子午风在夜间产生很强的向上漂移，在白天产生向下漂移，造成了hmF2的昼夜差，而在低纬地区这种昼夜差逐渐减弱至反号.由图9a2、a4、b2、b4可知，hmF2在夏季半球高于冬季半球，这与已知的hmF2季节变化特征相符(熊年禄等，1999)，这可能是因为白天的盛行风场是夏季半球吹向冬季半球.

5　结论

本文利用非线性多项式构建了全球hmF2经验模型NPPHM，模型中包含315个系数，自变量包括太阳活动指数、地磁指数、地理经度、地方时和年积日.将来自CHAMP、GRACE和COSMIC的掩星数据按照纬度划分为71个不同纬度带，分别在这些纬度带内通过最小二乘拟合最终得到71组系数.经过对NPPHM和IRI2012的检验，本文得到以下结论：

(1) 分别利用NPPHM和IRI2012对建模使用的掩星数据源进行模拟， NPPHM平均偏差远小于IRI2012，说明建模的拟合效果较好.

(2) 利用建模数据源以外的GRACE掩星数据独立检验.NPPHM和IRI2012在太阳活动低年(2008年)与GRACE数据的相关系数分别为0.798和0.532，均方根误差分别为25.97 km和44.56 km；在太阳活动高年(2012年)的相关系数分别为0.732和0.488，均方根误差分别为31.39 km和42.83 km.

(3) 选取代表全球不同区域的地面测高仪数据并引入相似离度对NPPHM和IRI2012进行对比分析表明，NPPHM在全球绝大部分测站优于IRI2012，它在数值和变化形态上都与测高仪观测更加相似.

(4) 使用测高仪Athens站2003—2013年hmF2的月均值与NPPHM及IRI2012比较.长期来看，IRI2012与测高仪数据偏差较大，达8.11%，而NPPHM高低值分布及变化趋势都与测高仪数据比较一致，且偏差仅为3.53%.

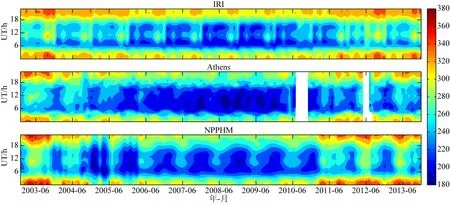
图8　2003—2013年Athens站IRI2012(上)、测高仪(中)和NPPHM(下)月均值随世界时的变化Fig.8　Diurnal variations of monthly mean of IRI2012 (top)，ionosonde observation (middle) and NPPHM (bottom) as a function of UT from 2003 to 2013 in Athens

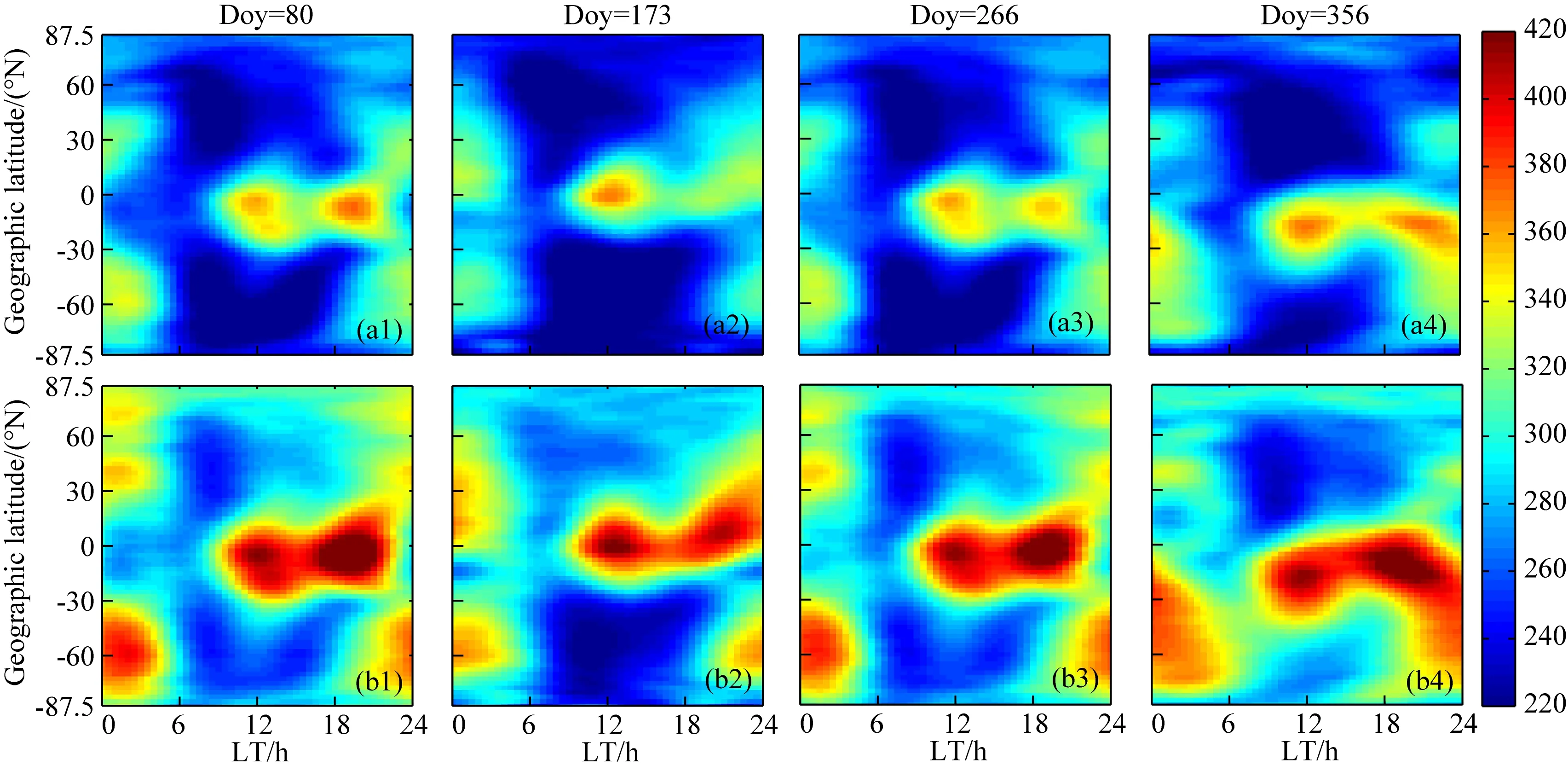
图9　NPPHM随纬度和地方时的变化(Lon=70°W，Ap=5)上一行表示太阳活动低年(F10.7=80)，下一行表示太阳活动高年(F10.7=120)；从左至右分别表示春分日(Doy=80)、夏至日(Doy=173)、秋分日(Doy=266)和冬至日(Doy=356).Fig.9　Variations of NPPHM as functions of latitude and local time(Lon=70°W，Ap=5)The upper panel represents low solar activity year (F10.7=80), the lower panel represents high solar activity year(F10.7=120); from left to right is spring equinox (Doy=80),summer solstice(Doy=173),autumn equinox(Doy=266) and wintersolstice(Doy=356).

(5) NPPHM能够较好的模拟hmF2的日变化、季节变化及赤道异常等特性.

本文采用的非线性多项式模型也可以用于对电离层电子总含量(TEC)及F2层峰值密度(NmF2)的建模中.今后可以进一步补充建模原始数据，尤其是太阳活动高年、高纬地区和来自赤道地区测高仪的数据，以使模型更加完善.

致谢感谢German Aerospace Center(DLR) Neustrelitz提供CHAMP和GRACE卫星电离层探测数据，感谢CDAAC(COSMIC Data Analysis and Archive Center)提供COSMIC卫星电离层探测数据，感谢SPIDR(Space Physics Interactive Data Resource)提供地面测高仪探测数据.感谢国家自然科学基金(40505005)的支持.

Altadill D, Magdaleno S, Torta J M, et al. 2013. Global empirical models of the density peak height and of the equivalent scale height for quiet conditions.Adv.SpaceRes., 52(10): 1756-1769. Bilitza D, Eyfrig R, Sheikh N M. 1979. A global model for the height of the F2-peak using M3000 values from the CCIR numerical map.ITUTelecommun.J., 46: 549-553.

Bilitza D. 1990. International reference ionosphere 1990, NSSDC 22-90. Greenbelt, Maryland, USA: National Space Science Data Center.

Bilitza D, Reinisch B W. 2008. International reference ionosphere 2007: Improvements and new parameters.Adv.SpaceRes., 42(4): 599-609.

Bilitza D. 2015. The international reference ionosphere-Status 2013.Adv.SpaceRes., 55(8): 1914-1927.

Brunini C, Conte J F, Azpilicueta F, et al. 2013. A different method to update monthly medianhmF2values.Adv.SpaceRes., 51(12): 2322-2332.

Garcia-Fernandez M, Hernandez-Pajares M, Juan M, et al. 2003. Improvement of ionospheric electron density estimation with GPSMET occultations using Abel inversion and VTEC information.J.Geophys.Res., 108(A9): 1338. Hajj G A, Romans L J. 1998. Ionospheric electron density profiles obtained with the global positioning system: Results from the GPS/MET experiment.RadioSci., 33(1): 175-190.

Hoque M M, Jakowski N. 2012. A new global model for the ionospheric F2 peak height for radio wave propagation.Ann.Geophys., 30(5): 797-809.

Kakinami Y, Watanabe S, Oyama K I. 2008. An empirical model of electron density in low latitude at 600 km obtained by Hinotori satellite.Adv.SpaceRes., 41(9): 1495-1499.

Kakinami Y, Chen C H, Liu J Y, et al. 2009. Empirical models of total electron content based on functional fitting over Taiwan during geomagnetic quiet condition.Ann.Geophys., 27(8): 3321-3333.

Krankowski A, Zakharenkova I, Krypiak-Gregorczyk A, et al. 2011. Ionospheric electron density observed by FORMOSAT-3/COSMIC over the European region and validated by ionosonde data.J.Geod., 85(12): 949-964.

Kutiev I S, Marinov P G, Watanabe S. 2006. Model of topside ionosphere scale height based on topside sounder data.Adv.SpaceRes., 37(5): 943-950.

Lei J H, Syndergaard S, Burns A G, et al. 2007. Comparison of COSMIC ionospheric measurements with ground-based observations and model predictions: Preliminary results.J.Geophys.Res., 112(A7): A07308.Li K Y. 1986. A new similarity parameter and its application.ActaMeteor.Sinica(in Chinese), 44(2): 174-183.

Lin J, Yue X A, Zeng Z, et al. 2014. Empirical orthogonal function analysis and modeling of the ionospheric peak height during the years 2002-2011.J.Geophys.Res., 119(5): 3915-3929. Liu H, Lühr H. 2005. Strong disturbance of the upper thermospheric density due to magnetic storms: CHAMP observations.J.Geophys.Res., 110(A9): A09S29. Liu H X, Hirano T, Watanabe S. 2013. Empirical model of the thermospheric mass density based on CHAMP satellite observations.J.Geophys.Res., 118(2): 843-848.

Magdaleno S, Altadill D, Herraiz M, et al. 2011. Ionospheric peak height behavior for low, middle and high latitudes: A potential empirical model for quiet conditions-comparison with the IRI-2007 model.J.Atoms.SolarTerr.Phys., 73(13): 1810-1817. Müller S, Lühr H, Rentz S. 2009. Solar and magnetospheric forcing of the low latitude thermospheric mass density as observed by CHAMP.Ann.Geophys., 27(5): 2087-2099.

Radicella S M, Leitinger R. 2001. The evolution of the DGR approach to model electron density profiles.Adv.SpaceRes., 27(1): 35-40.

Rawer K, Ramakrishnan S, Bilitza D. 1978. International Reference Ionosphere, International Union of Radio Science. Special Report. Brussels, Belgium. Shubin V N, Karpachev A T, Tsybulya K G. 2013. Global model of the F2layer peak height for low solar activity based on GPS radio-occultation data.J.Atoms.SolarTerr.Phys., 104: 106-115. Shubin V N. 2015. Global median model of the F2-layer peak height based on ionospheric radio-occultation and ground-based Digisonde observations.Adv.SpaceRes., 56(5): 916-928.Weng L B, Fang H X, Xie Y Q, et al. 2011. Application of analog prediction method on ionospheric TEC short-term forecast.ChineseJ.SpaceSci. (in Chinese), 31(6): 747-753.

Xiong N L, Tang C C, Li X J. 1999. Introduction of the Ionospheric Physics (in Chinese). Wuhan: Wuhan University Press.

Yue X, Schreiner W S, Lei J, et al. 2010. Error analysis of Abel retrieved electron density profiles from radio occultation measurements.Ann.Geophys., 28(1): 217-222.

Yue X A, Schreiner W S, Kuo Y H, et al. 2015. Ionosphere equatorial ionization anomaly observed by GPS radio occultations during 2006-2014.J.Atoms.SolarTerr.Phys., 129: 30-40.

Zhang M L, Liu C, Wan W, et al. 2009. A global model of the ionospheric F2peak height based on EOF analysis.Ann.Geophys., 27(8): 3203-3212.

Zhang M L, Liu C X, Wan W X, et al. 2010. Evaluation of global modeling ofM(3000) F2andhmF2based on alternative empirical orthogonal function expansions.Adv.SpaceRes., 46(8): 1024-1031.

附中文参考文献李开乐. 1986. 相似离度及其使用技术. 气象学报, 44(2): 174-183. 翁利斌, 方涵先, 解妍琼等. 2011. 相似预报法在电离层TEC短期预报中的应用. 空间科学学报, 31(6): 747-753.

熊年禄, 唐存琛, 李行健. 1999. 电离层物理概论. 武汉: 武汉大学出版社.

(本文编辑汪海英)

Global model of ionospheric hmF2based on CHAMPE, GRACE and COSMIC radio occultation

LIU Zhen-Di1， FANG Han-Xian1*， WENG Li-Bin1， MA Qiang1， ZHANG Jian-Bin2

1InstituteofMeteorologyandOceanography,PLAUniversityofScienceandTechnology,Nanjing211101,China2UnitNo. 63655ofPLA,Urumqi841700,China

For global ionospherichmF2modeling, a nonlinear polynomial model approach based on globalhmF2observational data form ionospheric radio occultation (IRO) measurements onboard CHAMP, GRACE, and COSMIC satellites is presented in this paper. The Nonlinear Polynomial Peak Height Model (NPPHM) is constructed by a nonlinear fit withhmF2measurements in least squares sense and describes the dependencies ofhmF2on geomagnetic activity, solar activity, geographical longitude, local time, day of year and geographical latitude. Using independent data from CHAMP satellite, quantitative analysis is made. The correlation coefficients for proposed model NPPHM and CHAMP data are 0.798 in 2008 and 0.732 in 2012, respectively. The corresponding coefficients for IRI2012 are 0.532 and 0.488. NPPHM shows root mean squared errors (RMS) of 25.97 km and 31.39 km in 2008 and 2012, respectively. The corresponding values for IRI2012 are 44.56 km and 42.83 km. Analog deviations are calculated to compare the NPPHM with IRI2012, using data from 14 different world wide ionosonde stations. The deviation of NPPHM is much less than that of IRI2012. Using observational data from the Athens station from 2003 to 2013, the mean deviation of IRI2012 is 8.11%, more than 3.53% of NPPHM. In low solar activity years and every October during the 11 years, the accuracy of NPPHM is much higher than that of IRI2012. What’s more, NPPHM can well present the daily variation, seasonal variation and equatorial ionization anomaly phenomenon ofhmF2.

IonospherichmF2modeling； Nonlinear polynomial； Radio occultation data

10.6038/cjg20161003.

国家自然科学基金项目(40505005)资助.

刘桢迪,男,1991年生,硕士研究生,研究方向为电离层物理.E-mail:lzdion@163.com

方涵先,男,1974年生,教授,博士生导师,研究方向为电离层物理.E-mail:fanghxp@163.com

10.6038/cjg20161003

P352

2015-10-09，2016-01-25收修定稿

刘桢迪， 方涵先， 翁利斌等. 2016. 基于CHAMP、GRACE和COSMIC掩星数据的全球电离层hmF2建模研究. 地球物理学报，59(10):3555-3565,

Liu Z D， Fang H X，Weng L B,et al. 2016. Global model of ionospherichmF2based on CHAMPE, GRACE and COSMIC radio occultation.ChineseJ.Geophys. (in Chinese),59(10):3555-3565,doi:10.6038/cjg20161003.