两种量热模式下物质热分解的动力学补偿效应
尹瑞丽 陈利平,* 陈网桦 吴 珂张彩星 李 焓 于 诚
(1南京理工大学化工学院安全工程系,南京210094;2常州出入境检验检疫局,江苏常州213003)
两种量热模式下物质热分解的动力学补偿效应
尹瑞丽1陈利平1,*陈网桦1吴珂2张彩星1李焓1于诚1
(1南京理工大学化工学院安全工程系,南京210094;2常州出入境检验检疫局,江苏常州213003)
热分析量热仪主要包括动态、等温、恒温及绝热四种操作模式。很多学者基于动态及等温模式的测试结果,采用Arrhenius速率常数进行动力学计算,进而发现了所谓的“动力学补偿效应”。为了解绝热模式下是否也存在动力学补偿效应,分别采用绝热加速量热法(ARC)及动态差示扫描量热法(DSC)研究了过氧化二异丙苯(DCP)、40%(质量分数,下同)DCP溶液、葡萄糖、45%葡萄糖溶液的热分解特性,在此基础上基于Arrhenius公式计算了对应的表观活化能E和指前因子A,并对计算结果进行了分析。结果表明:绝热模式下,不同质量的同种样品及其溶液的最佳动力学参数,或者同一组数据采用不同的反应级数获得的lnA和E之间均存在明显的线性关系。此外,尽管由动态DSC数据计算获得的E和lnA普遍小于绝热模式的结果,但两种模式下获得的lnA和E之间仍然存在动力学补偿效应。由此可以推断,具有相同或类似反应机理的反应,虽然实验模式不同,但其E和lnA之间存在明显的动力学补偿效应。
动力学补偿效应;绝热模式;动态模式;活化能;指前因子
doi:10.3866/PKU.WHXB201511023
1 引言
热分析及量热方法在科学研究和生产实践中的应用越来越广泛,其主要研究物质(料)在各种热环境下发生各种物理、化学变化的过程1。求解描述某反应的“动力学三因子”(表观活化能E、指前因子A和反应机理函数f(α))是热分析动力学研究的目的2。而求解E和A常用Arrhenius公式3,4:

上式中T为开氏温度;R为气体常数;k为反应速率常数。
理论上,动力学三因子应该是相互独立的变量。然而,1976年,Gallagherh和Johnson5首先在Cu催化C2H5OH脱水反应中发现了所谓的动力学补偿效应(kinetic compensation effect),即lnA与E呈线性关系的现象,表达式为:

上式中a和b为补偿参数,a的单位2是mol∙kJ-1。
随后,更多学者发现了类似的现象,如张冬梅6、Qin7、Pouretedal8等对动态模式的热分析数据进行动力学计算,发现了lnA与E的线性关系;Pouretedal等还进一步根据lnA与E的线性关系预测了A的值。陈鸿伟等9则基于等温模式的测试结果发现了该现象。同时,还有学者尝试从样品与反应过程的物理化学性质,实验的各种因素和动力学计算的数学结果等方面对这种现象进行探讨10-15。文献16指出动力学补偿效应的存在是Arrehnius速率常数指数形式的必然结果,并利用数学方法进行了证明。
尽管已有报道对动力学补偿效应进行研究,然而这些研究都是基于动态模式(线性升温)或等温模式下的实验数据而开展的。实际上,动力学分析在绝热测试与分析中同样需要,但目前尚无这方面的报道。
过氧化二异丙苯(DCP)受热易分解,其分解热非常大,采用较小的样品量,最大温升速率就会超过ARC的跟踪速率。为了降低DCP的反应热,同时选用质量分数为40%的DCP的乙苯溶液(40% DCP)进行研究。乙苯在测试温度范围内不参加反应。因此,理论上DCP和40%DCP的动力学参数必然有相关之处。
为了研究不同分解机理的样品,获得的动力学参数是否有显著不同,选择分解机理与DCP不同的葡萄糖和45%葡萄糖水溶液进行测试。
因此本文利用绝热加速量热仪(ARC)对以上4种样品进行绝热测试及动力学计算,进而将结果与差示扫描量热法(DSC)动态模式下的动力学参数进行比较,探讨两种模式下的动力学补偿效应。
2 试剂和实验条件
2.1试剂
过氧化二异丙苯,99.5%(w,质量分数,下同),阿拉丁试剂;乙苯,98.5%,国药集团化学试剂有限公司;葡萄糖(D-(+)-Glucose),大于99.5%,阿拉丁试剂。
待测样品为:DCP,40%DCP的乙苯溶液(40%DCP),葡萄糖,45%的葡萄糖水溶液(45%葡萄糖)。
2.2实验设备和测试条件
ARC:英国Thermal Hazard Technology公司生产的绝热加速量热仪(esARC)。
ARC测试条件:加热-等待-搜索模式,温升台阶5°C,检测灵敏度0.02°C∙min-1,等待时间10 min,样品球为钛球,比热容0.53 J∙g-1∙K-1。
绝热模式测试时,样品释放的热量有一部分不可避免地用来加热样品池,从而导致所测温度曲线也受其影响。因此需要采用热修正系数Ф进行修正17-20,热修正系数定义为:

对测得的绝热温升进行修正,得到:

由此得到样品的比放热量为:

式中,mcell为样品球的质量,g;Cpcell为样品球的比热,J∙g-1∙K-1;ms为样品质量,g;Cps为样品的比热,J∙g-1∙K-1;ΔT为实测绝热温升,°C;ΔTad为修正后的绝热温升,°C;H为修正后的比放热量,J∙g-1。
ARC测试中,4种样品的质量和对应的Ф值列于表1。

表1 ARC测试的样品质量及Ф值Table 1 Sample masses and Φ values inARC tests
DSC测试采用瑞士Mettler Toledo公司生产的DSC-1。DSC测试条件:DCP和40%DCP溶液的测试温升速率β分别为2、4、8、10 K∙min-1。样品质量如表2所示。葡萄糖和45%葡萄糖溶液的测试温升速率分别为1、4、8、10 K∙min-1,升温速率差别越大,得到样品的起始分解温度和峰温差别越大,求取活化能和指前因子时,数据拟合范围越宽,所以在对葡萄糖及其溶液测试时,升温速率改为1 K∙min-1。样品质量如表3所示。
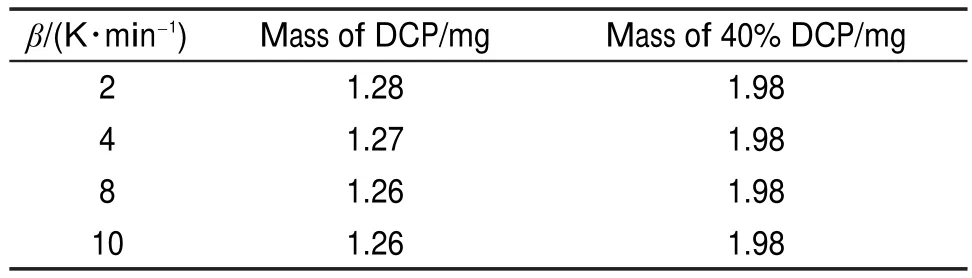
表2 DCP和40%DCP溶液的DSC测试质量Table2 MassesofDCPand40%DCPsolutioninDSCtests
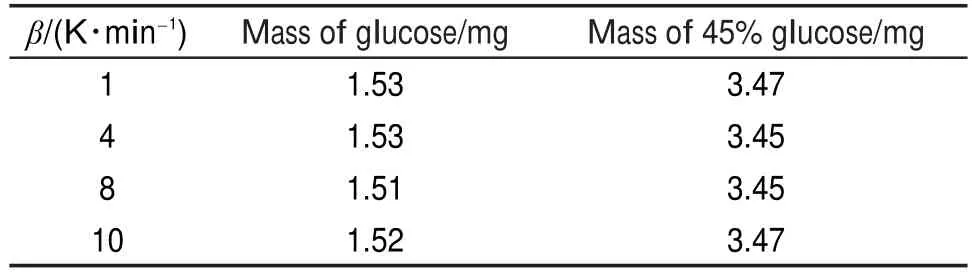
表3 葡萄糖和45%葡萄糖溶液的DSC测试质量Table 3 Masses of glucose and 45%glucose solutionin DSC tests
3 测试结果与讨论
3.1测试结果
3.1.1ARC绝热模式测试结果
表4和表5列出4种样品ARC的测试结果,包括样品起始分解温度To,°C;修正后的绝热温升ΔTad,°C;最大放热速率(dT/dt)m,°C∙min-1;修正后的放热量H,J∙g-1等参数。
由ARC测试结果可知,Ф值不同,样品球吸收的热量所占样品释放热量的比例不同,其温度和温升速率都是经过样品球吸热并经热量平衡后的结果。实测得到的起始分解温度、绝热温升、最大温升速率等均具有明显的差异。而对ARC数据进行动力学计算时,需要用到实测绝热温升和温升速率等参数,由于这些参数的差异,动力学计算结果必然不同。
3.1.2DSC动态模式测试结果
图1为4种样品的DSC测试结果。结果显示,温升速率越大,对应的起始分解温度和峰温越高。DCP和葡萄糖的DSC曲线能观察到明显的熔化吸热峰(峰向下),它们的溶液则不存在吸热峰。同时也可以发现,DCP与其溶液放热峰的峰型,起始温度等参数都比较接近,同样的现象也能在葡萄糖及其溶液中观察得到,其原因是作为溶剂的乙苯和水在测试的温度范围中很稳定,不参与反应。
3.2动力学计算
3.2.1基于绝热模式数据的动力学计算
绝热分解反应温度与温升速率的关系为:
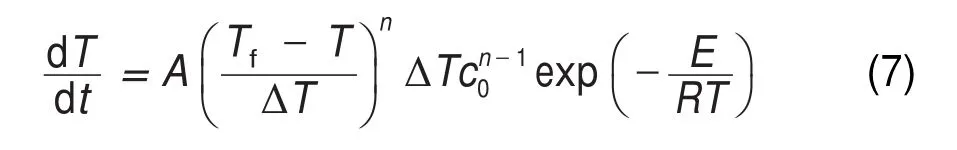
令:
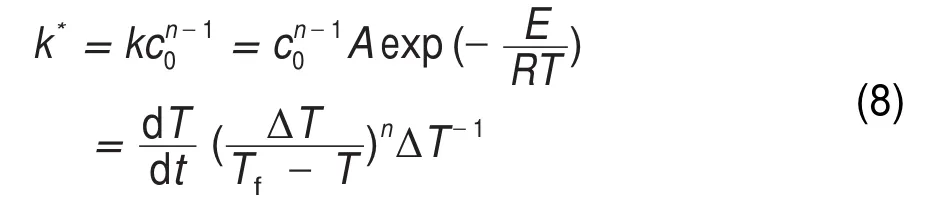
对(8)式两边取对数得:
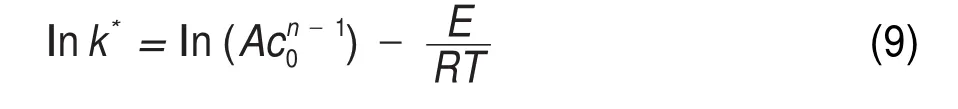
式中dT/dt为温升速率,°C∙min-1;Tf为分解终止温度,K;T为温度,K;c0为反应物初始摩尔浓度,mol∙L-1;n为反应级数17,21-23。

表4 DCP和40%DCP溶液的ARC测试结果Table 4 ARC test results of DCPand 40%DCPsolution
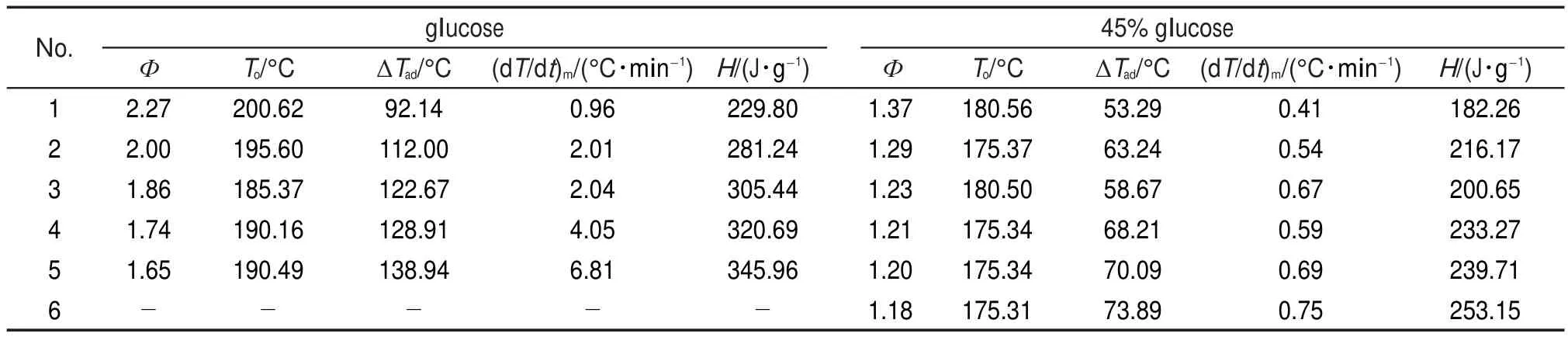
表5 葡萄糖和45%葡萄糖溶液的ARC测试结果Table 5 ARC test results of glucose and 45%glucose solution

图1 4种样品DSC的测试结果Fig.1 DSC test results of the four samples TS:sample temperature
选择合适的反应级数n,使方程(9)中lnk*与1/T的关系为直线。利用Origin软件进行拟合,由直线的斜率得到E,截距得到A。
采用上述方法对不同质量和Ф值的4种样品进行动力学计算,并将相关系数最高的计算结果列于表6和表7。

表6 DCP和40%DCP溶液的lnA与E的计算结果Table 6 Calculated results of lnAand E for DCPand 40%DCPsolution
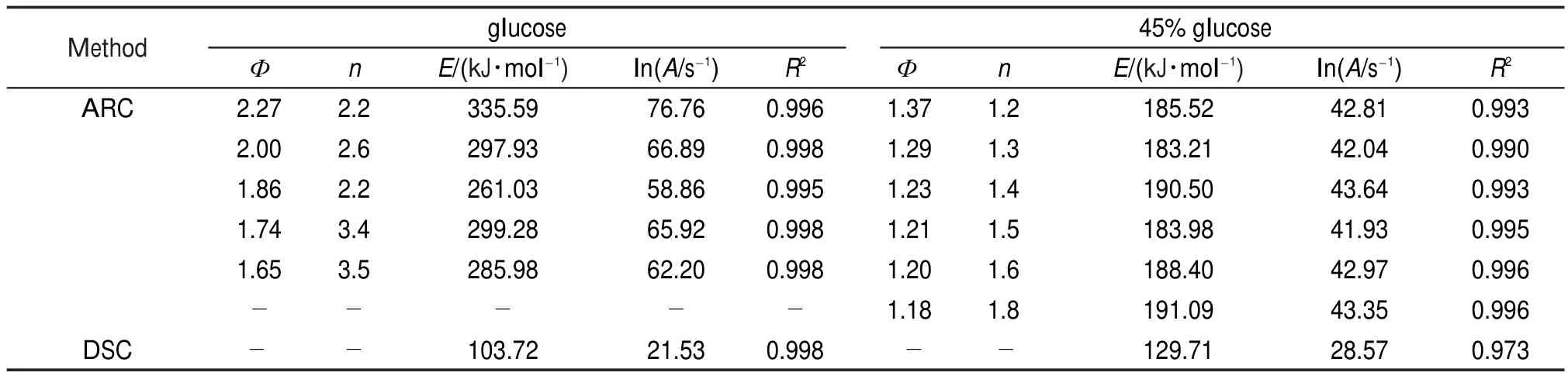
表7 葡萄糖和45%葡萄糖溶液的lnA与E的计算结果Table 7 Calculated results of lnAand E for glucose and 45%glucose solution
由表6和表7可知,基于绝热模式数据计算lnA和E时,相关系数较高,说明选择的n是可靠的。同时可以发现,如上文所述的现象,即不同Ф下的相同样品,由于实测起始分解温度,绝热温升等参数不同,计算得到的动力学参数也不同。由于进行动力学计算时所用的数据为实测参数,因此基于不同Ф下计算得到的动力学参数,实际上描述的是该Ф下的反应速率与温度的关系,而不是该样品本身绝热分解的反应速率。
3.2.2基于动态模式数据的动力学计算

采用Kissinger方法24,25计算4种样品峰温处的E和lnA,其计算方法见式(10):上式中i对应不同的温升速率,Tpi为DSC测试的峰温,K;βi为温升速率,K∙min-1。由对作图,便可得到一条直线,从直线斜率求E,截距求lnA。计算结果同样列于表6和表7中。
3.3动力学补偿效应
3.3.1绝热模式
为了考察在绝热模式中动力学结果是否存在动力学补偿效应。图2给出了DCP和40%DCP溶液以及葡萄糖和45%葡萄糖溶液lnA和E的拟合曲线。图2显示溶于溶剂的样品绝热动力学结果和不含溶剂样品结果之间存在良好的线性关系,即不论是否含有溶剂,绝热模式下不同样品质量的绝热动力学参数E和lnA之间都存在良好的线性关系,即存在明显的动力学补偿效应。
此外,由表6和图2(a)可知,同一种样品在样品量不同时,相同n值得到的lnA和E之间具有较好的线性关系。然而表7和图2(b)显示不同样品量的实验,即使在不同反应级数n下得到的lnA和E之间也具有较好的线性关系。为了探索这种现象存在的原因,这里以40%DCP溶液,质量为1.005 g的实验数据为例,采用不同反应级数n对该测试结果进行处理,得到lnk*与1/T的关系(见图3),进而利用式(9)拟合得到不同反应级数下的lnA和E,拟合结果见表8。
将不同n下的lnA和E列于图4。显然,对同一组ARC数据,选用不同的反应级数n,得到的动力学参数之间存在明显的动力学补偿效应,并且其斜率(0.297)与图2(a)的斜率(0.306)几乎相等。这也是对同一样品不同样品质量的测试结果进行动力学计算时,尽管反应级数n值不同,lnA和E仍然存在良好线性关系的原因。
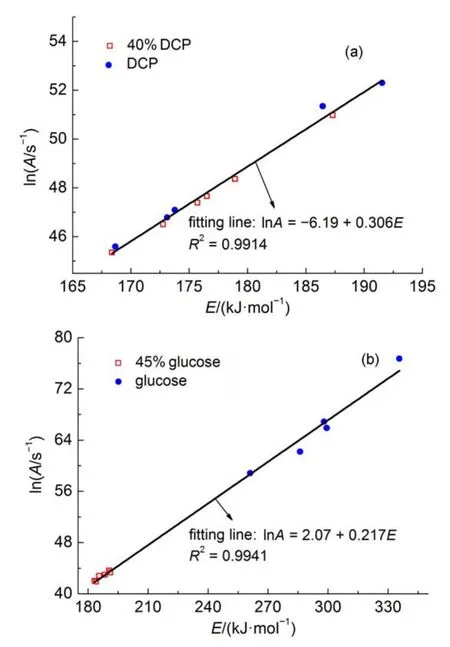
图2 在ARC数据基础上lnA和E的拟合结果Fig.2 Fitting results of lnAand E based onARC data
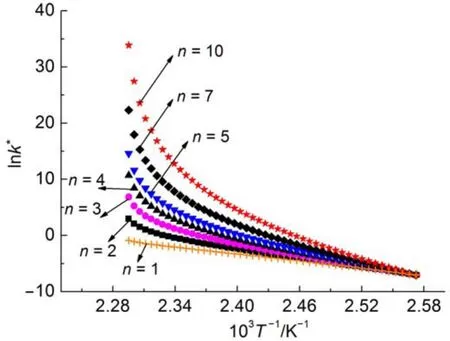
图3 同一组数据不同n计算得到的lnk*与1/T的关系Fig.3 Relationship between lnk*and 1/T with different n for the same set of data k*:pseudo rate constant
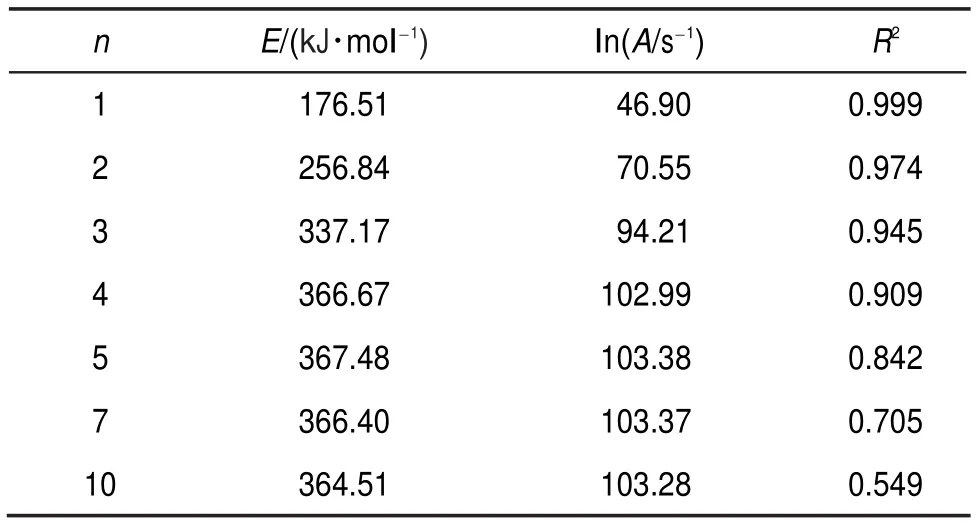
表8 同一组数据不同n计算得到lnA和E的值Table 8 Calculated lnAand E with different n for the same set of data
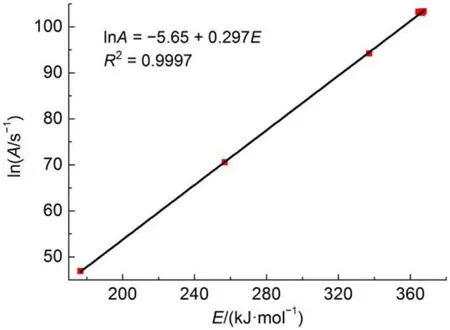
图4 同一组数据不同n计算得到的lnA和E的拟合结果Fig.4 Fitting results of lnAand E with different n for the same set of data
尝试将DCP、葡萄糖、40%DCP和45%葡萄糖溶液的动力学结果共同列于图5中,结果发现DCP和葡萄糖之间不存在动力学补偿效应(见图5)。而有关文献表明,性质相近的物质相同实验条件下进行同类型反应时,得到的动力学参数也具有明显的动力学补偿效应2。对比这两种截然不同的结果可知:具有相同或者相似的反应机理才会存在动力学补偿效应。
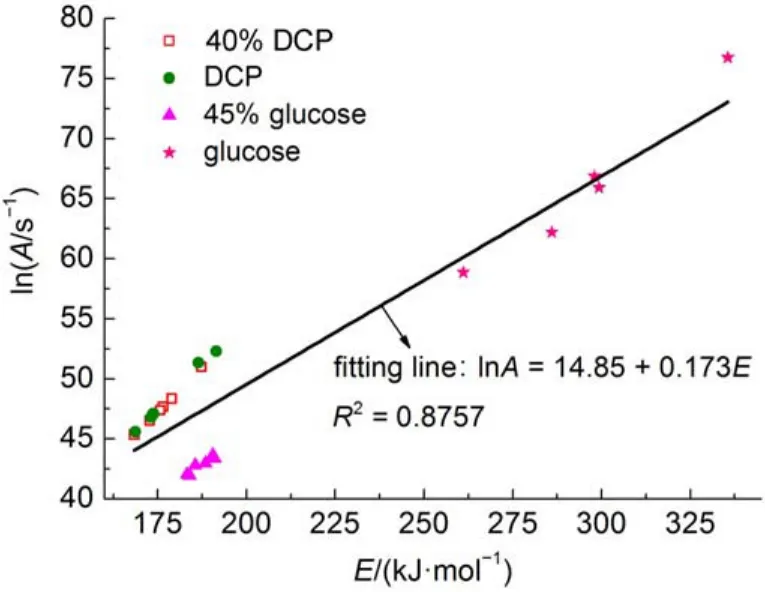
图5 在ARC数据基础上4种样品的lnA和E拟合结果Fig.5 Fitting results of lnAand E for four samples based onARC data
3.3.2绝热模式和动态模式结果
DSC的动态模式与ARC的绝热模式测试原理以及动力学参数的处理过程均不同。为了研究分别基于动态模式和绝热模式得到动力学处理结果之间是否同样存在动力学补偿效应,图6给出了DCP和40%DCP溶液,葡萄糖和45%葡萄糖溶液在动态模式和绝热模式测试基础上获得的E和lnA的关系。
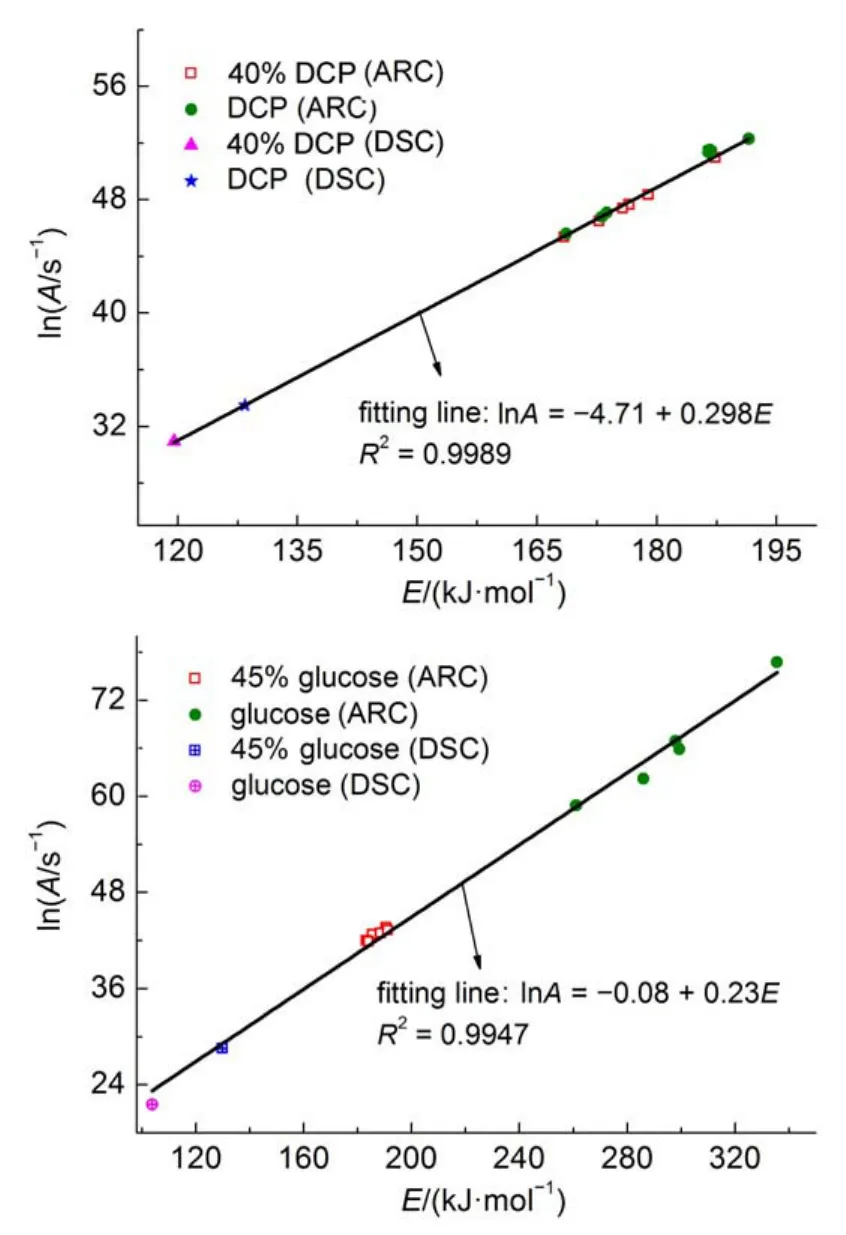
图6 在ARC和DSC数据基础上lnA和E的拟合结果Fig.6 Fitting results of lnAand E based on ARC and DSC data
结果显示,基于动态模式计算获得的E和lnA普遍小于基于绝热模式得到的结果,但是两者之间存在良好的动力学补偿效应。这从另一角度说明尽管测试模式不同,但是两类样品(DCP及其溶液,葡萄糖及其溶液)的反应机理并没有发生变化。
4 结论
采用ARC和DSC两种量热设备获得了4种样品(DCP、40%DCP溶液、葡萄糖、45%葡萄糖溶液)在绝热模式和动态模式下的热分解特性,进而计算得到活化能E和指前因子A。结果如下:
(1)绝热测试的样品量不同会导致起始分解温度、绝热温升等参数有所不同,但基于绝热模式计算得到DCP和40%DCP溶液之间,葡萄糖和45%葡萄糖溶液之间存在明显的动力学补偿效应。
(2)尽管绝热模式和动态模式的测试原理不同,且由动态模式获得的E和lnA普遍小于绝热模式的相应结果,但两种模式下相同样品及其溶液的lnA和E之间存在显著的动力学补偿效应。
(3)对绝热测得的数据采用不同反应级数n进行动力学分析时,得到的lnA和E之间也会存在动力学补偿效应。
(4)尽管操作模式不同,但是具有相同或相似反应机理的反应活化能和指前因子之间仍然会存在动力学补偿效应。
References
(1)Chen,J.H.;Li,C.R.Thermal Analysis and Its Application, 1th ed.;Science Press:Beijing,1985;pp 6-118.[陈镜泓,李传儒.热分析及其作用.第一版.北京:科学出版社,1985:6-118]
(2)Hu,R.Z.;Gao,S.L.;Zhao,F.Q.;Shi,Q.Z.;Zhang,T.L.; Zhang,J.J.Thermal Analysis Kinetics,2nd ed.;Science Press: Beijing,2008;pp 151-155.[胡荣祖,高胜利,赵凤起,史启祯,张同来,张建军.热分析动力学.第二版.北京:科学出版社,2008:151-155.]
(3)Tang,H.;Yan,Y.D.;Zhang,M.L.;Xue,Y.;Zhang,Z.J.;Du, W.C.;He,H.Acta Phys.-Chim.Sin.2013,29(8),1698.[唐浩,颜永得,张密林,薛云,张志俭,杜卫超,何辉.物理化学学报,2013,29(8),1698.]doi:10.3866/PKU. WHXB201305102
(4)Su,H.Z.;Yin,J.M.;Liu,Q.S.;Li,C.P.Acta Phys.-Chim. Sin.2015,31(8),1468.[宿洪祯,尹静梅,刘青山,李长平.物理化学学报,2015,31(8),1468.]doi:10.3866/PKU. WHXB201506111
(5)Gallagher,P.K.;Johnson,D.W.Thermochim.Acta 1976,14 (3),255.doi:10.1016/0040-6031(76)85002-2
(6)Zhang,D.M.;Zheng,C.M.;Heng,S.Y.;Liu,Z.R.;Pan,Q.; Lu,H.L.Chinese Journal of Explosives&Propellants 2014, 37(3),82.[张冬梅,郑朝民,衡淑云,刘子如,潘清,陆洪林.火炸药学报,2014,37(3),82.]
(7)Qin,Z.;Balasubramanian,S.K.;Wolkers,W.F.;Pearce,J.A.; Bischof,J.C.Annals of Biomedical Engineering 2014,42(12), 2392.doi:10.1007/s10439-014-1100-y
(8)Pouretedal,H.R.;Ravanbod,M.J.Therm.Anal.Calorim. 2015,119(3),2281.doi:10.1007/s10973-014-4330-1
(9)Chen,H.W.;Chen,J.T.;Wei,R.G.;Chen,L.Journal of Central South University:JCR-SC 2013,44(4),1695.[陈鸿伟,陈江涛,危日光,陈龙.中南大学学报:自然科学版, 2013,44(4),1695.]
(10)Barrie,P.J.Phys.Chem.Chem.Phys.2012,14(1),318.doi: 10.1039/C1CP22666E
(11)Yelon,A.;Sacher,E.;Linert,W.Phys.Chem.Chem.Phys. 2012,14(22),8232.doi:10.1039/c2cp40618g
(12)Zuniga-Hansen,N.;Silbert,L.E.;Calbi,M.M.Breakdown ofKinetic Compensation Effect in Physical Desorption.http:// arxiv.org/abs/1503.06362(accessed Mar 21,2015).
(13)Garn,P.D.Therm.Anal.1976,10(1),99.doi:10.1007/ BF02179195
(14)Brill,T.B.;Gongwer,P.E.;Williams,G.K.J.Chem.Phys. 1994,98(47),12242.
(15)Liu,T.T.;Ran,Y.Y.;Wang,B.C.;Dong,W.B.;Wu,S.G.; Gong,J.B.Front.Chem.Sci.Eng.2014,8(1),55.
(16)Koga,N.;Šesták,J.Thermochim.Acta 1991,182(2),201.doi: 10.1016/0040-6031(91)80005-4
(17)Townsend,D.I.;Tou,J.C.Thermochim.Acta 1980,37(1),1. doi:10.1016/0040-6031(80)85001-5
(18)Stoessel,F.Thermal Safety of Chemical Process:Risk Assessment and Process Design;Science Press:Beijing,2009; pp 73-74;translated by Chen,W.H.,Peng,J.H.,Chen,L.P. [Stoessel,F.化工工艺热安全:风险评估与工艺设计.陈网桦,彭金华,陈利平,译.北京:科学出版社,2009:73-74.]
(19)Lu,K.The Influence of the TypicalAdditives of Emulsion Explosives on the Thermal Decomposition of Emulsion Explosives.M.S.Dissertation,Nanjing University of Science and Technology,Nanjing,2009.[鲁凯.乳化炸药中典型组分对其热分解行为影响的研究[D].南京:南京理工大学, 2009.]
(20)Fisher,H.G.;Forrest,H.S.;Grossel,S.S.;Huff,J.E.;Muller, A.R.;Noronha,J.A.;Shaw,D.A.;Tilley,B.J.Emergency Relief System Design Using DIERS Technology:The Design Institute for Emergency Relief Systems(DIERS)Project Manual;John Wiley&Sons:New York,2010:pp 385-395.
(21)Liu,R.H.;Chen,W.H.;Hu,Y.T.Safety Principle and Dangerous Chemicals Assessment Technology,1st ed.; Chemical Industry Press:Beijing,2004;pp 158-163.[刘荣海,陈网桦,胡毅亭.安全原理与危险化学品测评技术.第一版.北京:化学工业出版社,2004:158-163.]
(22)Chen,L.P.Experimental and Theoretical Studies on Thermal Hazards of Toluene Nitrations.Ph.D.Dissertation,Nanjing University of Science and Technology,Nanjing,2009.[陈利平.甲苯硝化反应热危险性的实验与理论研究[D].南京:南京理工大学,2009.]
(23)Zhou,Y.S.;Chen,L.P.;Chen,W.H.;Yang,T.;Zhang,C.X.; Yin,R.L.CIESC Journal 2014,65(11),4383.[周奕杉,陈利平,陈网桦,杨庭,张彩星,尹瑞丽.化工学报,2014,65 (11),4383.]
(24)Kissinger,H.E.Anal.Chem.1957,29(11),1702.doi:10.1021/ ac60131a045
(25)Peng,M.J.;Lu,G.B.;Chen,W.H.;Chen,L.P.;Lü,J.Y.Acta Phys.-Chim.Sin.2013,29(10),2095.[彭敏君,路贵斌,陈网桦,陈利平,吕家育.物理化学学报,2013,29(10),2095.] doi:10.3866/PKU.WHXB201307122
Kinetic Compensation Effect under Two Different Calorimetric Modes for Thermal Decomposition
YIN Rui-Li1CHEN Li-Ping1,*CHEN Wang-Hua1WU Ke2ZHANG Cai-Xing1LI Han1YU Cheng1
(1Department of Safety Engineering,School of Chemical Engineering,Nanjing University of Science and Technology,Nanjing 210094, P.R.China;2ChangzhouEntry-ExitInspectionandQuarantineBureau,Changzhou 213003,JiangsuProvince,P.R.China)
Thermal analysis calorimeters can be used with different temperature control modes.Dynamic, isothermal,isoperibolic,and adiabatic modes are commonly used.A kinetic compensation effect was discovered when the kinetic parameters were calculated using the Arrhenius equation,based on dynamic and isothermal data.To determine whether the kinetic compensation effect existed in adiabatic mode, accelerating rate calorimetry(ARC)and differential scanning calorimetry(DSC)were used to obtain thermal decomposition curves of dicumyl peroxide(DCP),40%(w)DCP in ethylbenzene,glucose,and 45% (w)glucose in water.The apparent activation energies(E)and pre-exponential factors(A)were calculated based on the Arrhenius rate constant.An obvious kinetic compensation effect was observed in a plot of lnA vs E for a given sample at different concentrations or for the same set of ARC data analyzed with different reaction orders n.Although the calculated lnA and E values using the dynamic differential scanning calorimetry data were usually lower than those using the adiabatic ARC data,a significant kinetic compensation effect existed between the two sets of results.This result suggested that the kineticcompensation effect existed between the activation energy and pre-exponential factor in reactions with the same or similar reaction mechanisms,regardless of the temperature control mode.
Kinetic compensation effect;Adiabatic model;Dynamic model;Activation energy; Pre-exponential factor
October 6,2015;Revised:November 2,2015;Published on Web:November 2,2015.
O643;O642
*Corresponding author.Email:clp2005@hotmail.com;Tel:+86-25-84315526-8004.
The project was supported by the National Natural Science Foundation of China(51204099)and Science and Technology Plan Projects of Jiangsu Entry-Exit Inspection and Quarantine Bureau,China(2014KJ59).
国家自然科学基金(51204099)和江苏出入境检验检疫局科技计划(2014KJ59)资助项目
©Editorial office ofActa Physico-Chimica Sinica

