刍议数学语言能力在高中数学解题中的重要性

张温欣

（青岛第五十八中学高三学生）

刍议数学语言能力在高中数学解题中的重要性

张温欣

（青岛第五十八中学高三学生）

在我国现阶段高中教育领域中，数学考试不仅对学生的数学知识进行考核，还对其数学语言能力提出要求。数学语言既是数学知识与数学思维的语言载体，也是学生学习高中数学知识与解答习题的重要工具。本文首先分析高中数学语言分类与特点，随后研究其在解题中的重要性，以期为学生更好学习数学做出贡献。

数学语言能力 高中数学 解题

数学是一门抽象性与逻辑性较强的学科，在高中阶段，如何学好数学一直是我们学生难以破解的难题。数学语言可以在学生解题方面发挥不可忽视的作用，因此，我们必须尽快提高自身数学语言能力，以便于快速解决数学问题，在提高自身学习成绩、学习高中数学上更加得心应手。［1］

一、分类与特点

1.分类

在高中数学学习中，我们在归纳以后可以将数学语言大致分为表达类与知识版块类，表达类可以细化分为文字、图标与符号语言三种；知识版块类可以细化分为集合与逻辑、复数、函数、几何、计算机、代数语言等。

2.特点

高中数学语言具有精准性、简约性、符号化与形式化、抽象性、通用性、可操作性六大特点。数学定义、定理、公理与推理组成数学学科的逻辑系统，这些都需要使用精准性强的数学语言表达，在数学学科中，每一个词语或符号所表达的意义都是十分确定、不存在歧义的，具有极为精确的内涵。对于定理或者命题来说，条件需要充分必要、结论需要合理、推理论证过程需要缜密。高中数学运算要求我们必须掌握精确和具有逻辑性的数学语言，只有这样，才能准确表述数学对象的规律与本质属性，在解题过程中得出的数学理论才可以经得住考验。［2］

在学习过程中我们可以得知，数学语言具有简洁性与精炼性，使用数学语言阐述数学规律、定理与概念时，可以确保将数学推理、计算与表达更加明确清晰。数学语言形式化与符号化主要表现在数学推理与计算过程中，数学语言可以使数学推理与计算更具可靠性与可操作性，其结论更经得住检验与推敲。符号化与形式化不仅是数学发展的最终结果，还能使数学更加方便运用与操作。

高中数学学习过程中，许多学习到的推理、定理与定义多数都是生活经验的抽象概括，主要表现为使用数学符号与概括数学语言等。在数学语言中，通用性表现为在同一数学问题上，数学语言表述不同，其应用广泛，既可以表达数学思维与数学知识，也可以表述物理化原理。除此以外，在深入学习以后我们可以发现，高中数学问题能根据可操作性特点，利用数学中的已知定理、运算与规律分析，讲逻辑推理变为图表或运算形式解决问题，从而得出结论。

二、重要性

1.数学语言能力可以拓展解题思路

数学语言具有转换能力，这种能力就是指对数学语言不同表达形式互相转换或与同种表达形式内部等价转换，数学语言转换可以帮助我们有效解决数学难题，拓宽解题思路，尤其是在数形结合等领域中，数学语言可以利用问题、结构、等价与易元转换等方法引发联想，激发灵感，为解题提供线索与多种思路。［3］

在高中数学学习过程中，每一个数学概念、语义与关系都具有数学语言表达，但是，同种数学语义存在不同数学语言表达，同种数学语言表达又存在不同语义解释，转换数学语言必须注重等价交换，这表明，我们可以利用数学语言语义与形式转换，分析数学对象不同角度的性质与特征，进而发现解题思路，明确解题方向，确定解题方法。

将C1参数方程转化为极坐标方程；

（2）将C1与C2交点极坐标求出.

从题目可知，“参数方程”与“极坐标方程”都是表达曲线数学符号，只是表达角度不同，此时作为学生，在理解二者概念基础上，可以加入“普通方程”，利用形式转换公式实现解题母体，消除参数t，即x2+y201 6y1 0-x8-=+，转换极坐标方程与普通方程：

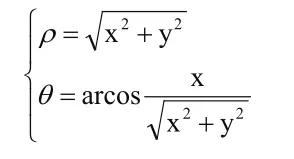
将坐标转换为极坐标形式，把C2极坐标方程根据转换公式转变为普通方程二者联立，可以得出交点坐标（1，1）与（0，2），利用转换公式将极坐标转换为2.数学语言能力是解题的基础与关键

数学语言中的理解能力就是指语义理解力，可以对数学问题中的概念、定理、条件、结论与公理表达的意义与关系进行理解，其具有三个层次，分别是理解数学名词、数学语言信息与信息间关系。数学语言理解包括挖掘数学题目中的隐含条件与辨析新定义，理解能力越强，对解决问题的帮助也就越大，例如在解题时，我们不仅需要明白它代表两数平方和，还需要联想其他语义，例如均值不等式、勾股定理、距离公式、向量与复数的模等。数学语言理解基于数学语言识别，在掌握命题中的基本信息与数学隐藏意义后，才能分析信息表达语义，寻找解题思路与方法。

例如笔者在做高考真题卷时遇到这样一道题：定义正对数：

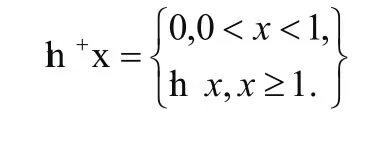
现有四个命题：

其中，真命题是（写出真命题编号）

这道题出现了对数函数表达与分段函数形式，“正对数”作为一个新定义概念，需要在解题时深入理解，明确认识数学符号结构以后，才能继续解题。篇幅有限，本文仅针对①命题进行分析，首先必须明确，“正对数”属于分段函数，在解决相关问题时，需要讨论自变量取值范围，除此以外，还需要明确的一点是，“ab”是指数形式，需要讨论“ab”取值。由于“ab”属于指数函数，因此需要分类讨论底数a的定义域，当此时命题成立；当a=1时，则命题成立；当a＞1时，ab＞1，则此时命题成立。因此命题①为真命题，命题③④真命题同理可证。

结语

综上所述，在高中阶段，数学语言能力具有十分重要的作用，因此我们必须加强这一阶段的数学学习力度，从自身角度出发提高数学语言能力，只有这样，才能真正拓展数学解题思维，改善难以掌握数学知识的学习困境，实现提高自身数学学习能力的学习目的。

［1］耿哲.数学语言能力在高中数学解题中的重要性［J］.中学数学教学参考，2015（21）.

［2］赵丽金.论学生数学语言能力在高中数学解题中的重要性［J］.中学教学参考， 2015（23）.

［3］刘强.浅析数学语言能力在高中数学解题中的重要性［J］.中学课程辅导：教师通讯，2015（12）.