混合分布的VaR非参数估计：对期货市场的实证分析

肖佳文，杨 政

（电子科技大学经济与管理学院，四川成都611731）

混合分布的VaR非参数估计：对期货市场的实证分析

肖佳文，杨 政

（电子科技大学经济与管理学院，四川成都611731）

基于价格走势的不同将金融市场分为平稳行情，趋势与震荡行情，用混合分布刻画资产收益的母体分布特征，提出一种新的VaR非参数估计方法.利用高频数据对市场状态分类，基于Bootstrap的核密度方法估计子分布，最后计算总体分布的VaR.选取股指期货，铜期货，橡胶期货，豆粕期货等四个期货品种进行实证研究，估计了不同置信水平下的多头和空头VaR.实证结果表明：新方法相较传统的GARCH族模型，多种基于厚尾分布的GARCH模型，混合正态GARCH模型以及方差—协方差法能够更准确地估计空头VaR与尾部风险.

VaR；混合分布；核密度估计；Bootstrap

1 引言

J.P.Morgan银行最早将在险价值（value at risk，VaR）运用于Risk Metrics模型［1］.Jorion在1997年给出了一个较为权威的定义：VaR描述了目标持有期某收益或损失概率分布的分位数，若α为给定的置信水平，则VaR为对应的1-α下分位数，按惯例该最大损失表示为正值［2］.VaR数学定义如下［3］：VaRα（X）=-inf｛x| P［X≤x·r］＞1-α｝.其中X为资产损益，r为调整参数（通常为1），α为置信水平.该定义表明VaR的本质就是估计分位数.由于VaR直观地给出潜在风险损失的大小，在实际应用中可以对不同头寸的风险进行比较，因此VaR成为了近年来金融市场应用最为广泛的风险度量工具之一.

金融资产收益率通常存在尖峰厚尾性［4］，波动集聚性［5］和杠杆效应［6］等特征.因此在使用基于正态分布假设和波动独立同分布假设的模型估计VaR时难以获得较好的估计效果.计算VaR的方法大致分为三类：参数方法，半参数方法与非参数方法.其中参数方法主要为GARCH族模型［7，8］：基于不同分布假定的GARCH模型（GARCH-t［9］，GARCH-GED［10］）和基于不同模型形式的GARCH模型（EGARCH［11］，IGARCH［12］，FIGARCH［13］，PGARCH［14］，GJR［15］等）.GARCH族模型能够较好地描述数据的波动集聚性，但是即使使用T分布或GED分布等厚尾分布假设也无法准确描述数据的厚尾特征.半参数方法主要为基于极值理论（Extreme Value Theory）的估计方法：传统的基于广义极值分布的分块样本极大值模型BMM（Block Maxima Model）［16］与门限超越模型POT（Peaks Over Threshold）［17］.此类模型只关注分布的尾部特征而无需了解整体分布的情况，其缺点在于难以描述波动的动态相关结构和难以确定模型参数（如数据分块长度，门限值）.非参数方法主要包括历史模拟法［18］，蒙特卡洛模拟法［19］，核密度估计法［20］，Bootstrap法［21］等.此类方法从样本分布入手，故能够较好地拟合数据的高峰厚尾特征，但是无法从模型层面描述收益率的波动集聚性.

现有的VaR估计方法大部分都将收益率的母体分布看做单一分布.通过历史数据估计母体分布的相关信息，进而得到VaR的估计.这种思路忽视了金融市场存在不同状态：当市场中无刺激信息时，金融资产价格走势较为平稳，在一个均值水平附近波动；当市场中出现利好或利空信息时，参与者会对信息进行反应，推动价格上升或下降.价格在不同行情中有明显不同的走势，因而收益率分布在不同行情中也是不同的.基于这种观察，本文将收益率的母体分布假定为一个混合分布，不同市场行情下的收益率分布为母体分布中不同的子分布，各子分布以一定概率随机出现.使用基于Bootstrap的核密度估计方法对子分布进行估计，得到子分布的VaR.然后将各子分布的VaR加权得到总体的VaR.

2 高频数据的子分布分类

记样本X为一随机变量，总体分布的样本来自K个不同的母体，则概率密度函数为

对于样本量为n的观测样本｛X1,X2,...,Xn｝，样本似然函数为

通过求解极大似然函数可以得到子分布出现概率的估计.在实际计算中，由于子分布概率密度函数的解析表达式未知，子分布出现概率的估计难以通过求解似然函数得到.本文使用训练样本中各子分布出现的频率，作为概率的近似估计.

记第i天的收益率为ri，对应的子分布类型为ki，用来估计检验样本中第i天的VaR的训练样本为训练样本即｛ri,ri+1,...,ri+n-1｝（n为训练样本量），则检验样本第i天两个子分布出现概率的近似估计为

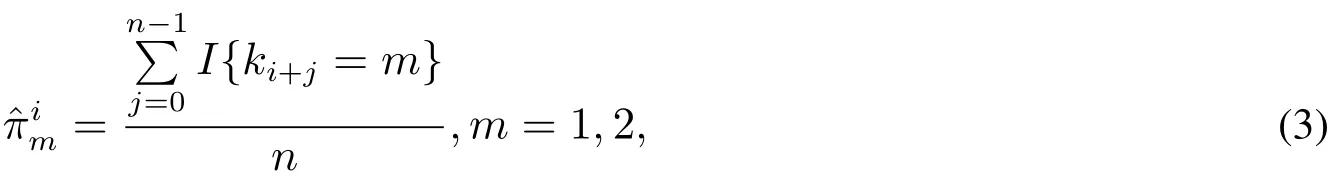
其中I｛·｝为示性函数，括号中条件成立时取值为1，反之为0.当子分布数量为2时，不同市场状态随机出现服从概率时变的二项分布.

要估计各子分布的出现概率，需要知道各样本（日收益率）所从属的子分布类型.本文根据信息对市场影响的强弱程度将市场状态分为平稳行情，趋势与震荡行情两类，即假定收益率母体分布由两个子分布构成.在平稳行情中，市场无刺激信息，价格在一个均值水平附近波动，价格序列可以视为均值非零的均值平稳时间序列.在趋势与震荡行情中，市场中有强度不等的刺激信息，受市场信息的影响，价格呈现趋势或震荡形态，价格均值是时变的，价格序列为非平稳序列.因此可以使用ADF检验来对行情进行分类.由于无常数项且无趋势项的ADF检验用于检验均值为0的均值平稳时间序列，有常数项和趋势项的ADF检验用于检验有线性趋势的趋势平稳时间序列.这两种检验都不合适.而带常数项的ADF检验用于检验均值不为0的均值平稳时间序列，在此处是合适的.所以通过对价格序列进行带常数项的ADF检验，对行情进行分类.带常数项的ADF检验的原假设H0与备择假设H1如下

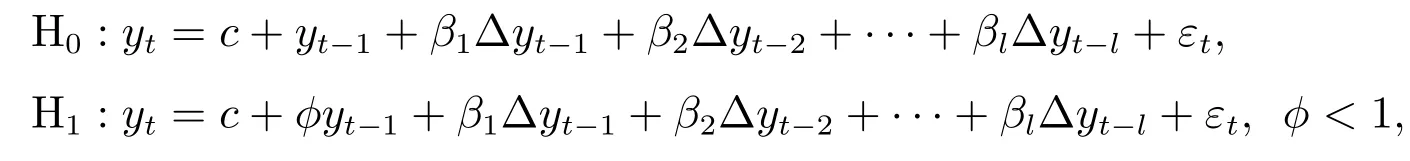
其中l为ADF检验的滞后阶数，最优滞后阶数可通过AIC准则确定.

计算中使用ADF检验的p值作为子样本分类的阈值，将p值小于0.1的定为平稳行情，p值大于0.1的定为趋势与震荡行情.对每日的1分钟收盘价序列进行带常数项的ADF检验，即可得到该日从属的子分布类型，进而用于估计训练样本中各子分布的出现概率.

3 基于非参数方法的子分布估计

在估计各子分布时，考虑到金融收益率的高峰厚尾特征，本文使用了基于Bootstrap的核密度估计方法.核密度估计方法作为一种非参数估计方法，不需要假定概率密度函数的解析表达式，能够较好地拟合金融收益率的高峰厚尾与非对称特征.Bootstrap方法是一种重抽样方法，能够较好地处理小样本问题.使用Bootstrap方法对核密度估计进行改进，可以在动态估计VaR时选取更小的训练样本，更快地对极端波动做出调整.在估计总体VaR时，首先估计各子分布的VaR，然后使用各子分布的出现概率作为权重，对子分布VaR加权得到总体的VaR.

3.1 Bootstrap方法

Bootstrap方法最早由Effron［22］于1979年提出，是一种针对小样本情况的估计方法.该方法在估计统计量时，不需要知道母体分布及待估计统计量的解析表达式.能够较好地解决母体分布未知和统计量解析表达式过于复杂带来的估计困难.其基本思想为：通过对样本进行多次有放回的随机抽样，得到多个原母体中存在但观测样本中未出现的新子样，从而获得更多有关母体分布的信息.可以证明Bootstrap方法在估计很多统计量时都满足大样本的一致性，比传统正态近似有更快的收敛速度.

使用Bootstrap方法估计分布F的1-α分位数q1-α的步骤如下：

步骤1 由观测样本｛X1,X2,...,Xn｝得到经验分布Fn（x）.令记步变量（用于记录已完成的Bootstrap抽样次数）i=1.

步骤2 对经验分布Fn进行有放回的随机抽样，得到Bootstrap子样

步骤4 若i＜k，令i=i+1，转至步骤2；若i=k，转至步骤5.其中k为设定的Bootstrap抽样总次数.

3.2 核密度估计

若观测值X1,X2,...,Xn为独立同分布的样本，则对于给定的核函数K与正的带宽（bandwidth）h，母体分布概率密度函数f（x）的核密度估计（kernel density estimator）定义为

在参数选择中，常用的核函数有均匀核，三角核，高斯核与Epanechikov核等，通常选择高斯核即可.较为重要的是带宽h的选择，n（x）对h的选择非常敏感，h直接影响着n（x）的光滑程度.一个渐进的最优带宽，可以通过对积分均方误差（AMISE）求h的微分，并令其为0求得.其中

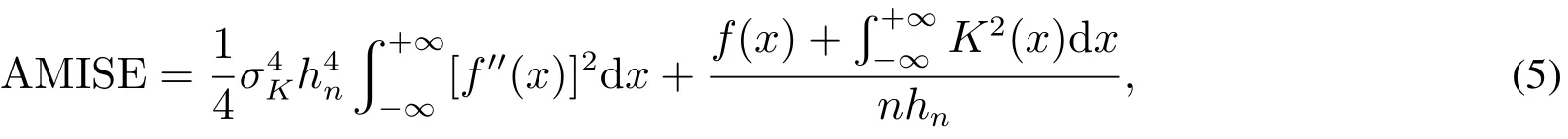
对应的渐进最优带宽为

在实践中带宽的计算方法通常为交叉验证法与插入带宽法.由于插入带宽法需要对概率密度函数做较强的假定，而这些假定不一定满足.因此本文选择交叉验证法计算带宽.该方法通过使交叉验证得分最小化来估计带宽h.交叉验证得分为

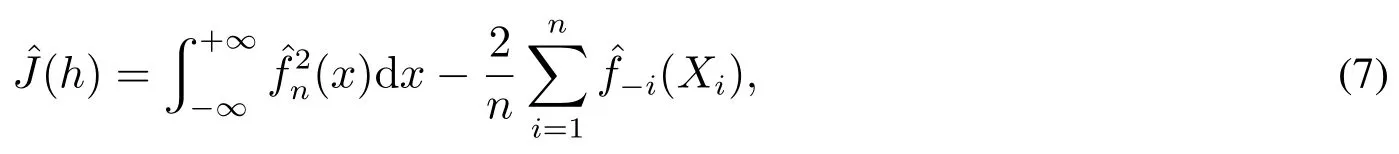
ˆJ的一个较简单的表示如下

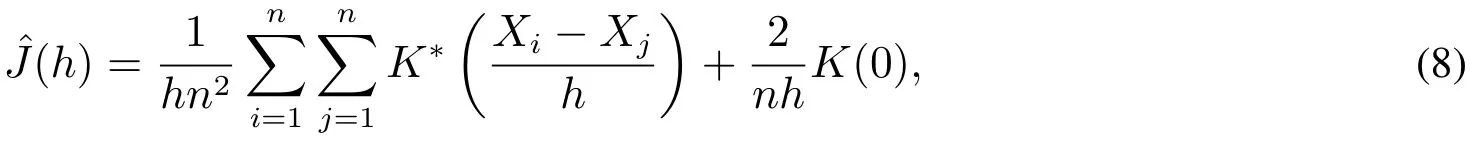
在高斯核条件下，根据VaRα的定义可知

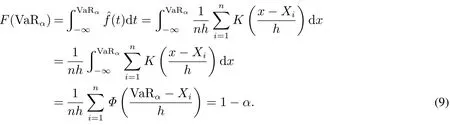
由于F（VaRα）=1-α，此时VaRα为估计出的母体分布函数（x）的1-α分位数.

4 实证分析

4.1 数据选取

本文在实证部分使用了中国金融期货交易所股指期货连续合约1分钟收盘价数据.选取的样本区间为2010年4月16日（股指期货上市日）至2013年4月10日，共723个交易日，每日270条分钟数据，总计195210条数据.股指期货是当前我国交易量与交易额最大的金融产品交易品种，2012年全年交易量为105061825手，总计交易额7584067787.796万元.由于股指期货拥有双向交易与T+0交易的特点.股指期货与股指现货相比有更大的交易额与更好的流动性，能够对市场信息进行较快调整，更充分地反映市场信息对金融产品价格波动带来的影响.本文数据来源为华西期货公司内部数据，数据处理与计算使用Matlab 2012b与R 3.1.0.

4.2 数据的基本分析

表1 沪深300股指期货收益率的统计特征Table 1 The statistical characteristics of CSI300 futures return

从表1可以看出，沪深300股指期货收益率的偏度为0.0441，轻微右偏.收益率的峰度为5.1743，有明显的尖峰特征.对比两种不同市场行情中收益率的峰度，平稳行情有较高的峰度.这是因为市场在盘整过程中，收益率在0附近波动，出现极端值的可能性很小.趋势及震荡行情的偏度为0.0128接近于0，峰度为4.9066较小.从波动性来看，趋势与震荡行情的波动（标准差）明显大于平稳行情，这也是符合常识的.正态性检验表明各情况下收益率均不服从正态分布.全样本收益率通过ADF检验，Ljung-Box Q检验，这表明日收益率数据为平稳序列，无自相关性.两种不同市场行情下收益率均通过BDS检验，满足样本相互独立假定，可以使用数据进行核密度估计.

4.3 VaR的计算及与其他方法的对比

本文计算VaR的步骤为：1）选取训练样本（训练样本量为120），通过对每个收益率样本当日的1分钟收盘价数据进行带常数项的ADF检验，对每个收益率样本从属的子分布进行分类；2）对各子分布的样本分别进行Bootstrap抽样；3）对每一个Bootstrap子样使用核密度估计方法估计给定置信水平下的VaR；4）对各子分布中所有Bootstrap子样的VaR加权得到各子分布的VaR；5）使用子分布的出现概率作为权重对子分布VaR进行加权，得到总体VaR.

在预测过程中，本文滚动选取训练样本进行1步预测.第一次预测选取第1个～120个样本作为第一组训练样本，估计第121天的收益率VaR.第二次预测选取第2个～121个样本作为第二组训练样本，估计第122天的收益率VaR，以此类推.实际的总检验样本量为602个，602个检验样本对应了602组训练样本.

在检验VaR估计方法是否有效时，使用了Kupiec提出的似然比检验［23］.给定检验样本中损失超过VaR的样本数量为N，总的检验样本数量为T，给定的置信水平为α，则对应的LR统计量为

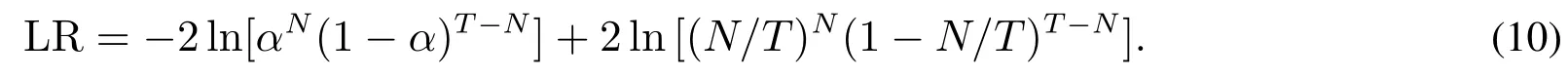
随时间推移，602组训练样本中两个子分布的出现概率变化与总交易量变化如图1所示.

从图1中可以看出，平稳行情的出现概率变化与交易量的变化是一致的，趋势与震荡行情的出现概率变化与交易量的变化是反向的.这是由于总交易量较小时，并不需要很大量的买单或卖单就会对价格带来冲击.因此无市场信息支撑的波动难以迅速平稳下来，异常波动较多，平稳行情较少.反之，交易量越大，参与者越多，市场对于信息的反映就更为准确，异常波动出现的概率较小.价格走势更为平稳，平稳行情出现的概率更大.随着时间推移，交易量先下降后上升，训练样本中趋势与震荡行情的出现概率先上升后下降，平稳行情的出现概率先下降后上升.这是由于股指期货上市后，沪深300指数先短暂上涨，然后迎来了一波长时间大跌，于2011年底到达谷底.这一段时期市场并不明朗，因而交易量先下降.其后，随着市场走势的企稳以及越来越多的交易者使用股指期货进行套利交易及风险对冲，交易量开始迅速增加.从图2可以看出，该方法能够较快地对市场的波动放大与波动缩小过程进行反映，同时也能较好体现多头VaR与空头VaR的非对称性.

图1 各组训练样本中两种市场状态的出现概率与总交易量Fig.1 Probability and volume of 2 market states in train samples

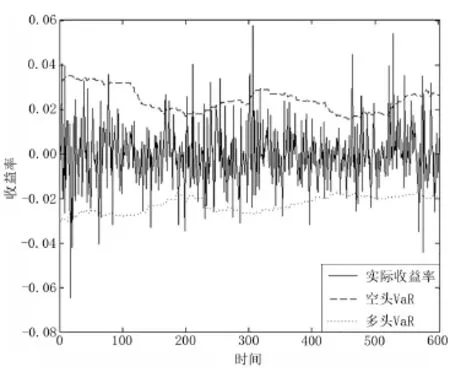
图2 95%置信水平下的VaR值与实际收益率对比Fig.2 Comparison between VaR and return at 95%confidence

表2 基于混合分布的VaR非参数估计结果Table 2 Nonparametric estimation result of VaR based on mixed distribution

VaR计算结果如表2所示，从表2可以看出，基于混合分布的VaR估计方法能够在各置信水平对多头与空头VaR进行有效估计，有较小的相对误差.在99%与95%两个置信水平下，该方法均通过Kupiec似然比检验（95%置信度，后同），是有效的VaR估计方法.

本文将该方法与参数法中常用的GARCH-N，GARCH-t，GJR模型，多种基于不同厚尾分布的GARCH模型（GARCH-GED，GARCH-skewed-t，GARCH-skewed-GED），混合正态GARCH模型（NM-GARCH）以及方差—协方差法进行了比较.由于GARCH族模型和方差—协方差法在估计时需要较大的训练样本.在比较中将GARCH族模型与方差—协方差法的训练样本量设为300，样本中的后422日作为检验样本.计算结果如表3所示.

从表3可知，1）从多头VaR来看，除GARCH-GED外所有模型在99%和95%两个置信水平下均通过似然比检验，是有效的VaR估计方法.在GARCH族模型中GARCH-t模型有最小的估计误差，估计效果比基于混合分布的VaR估计方法略好.其他基于厚尾分布的GARCH模型，如GARCH-GED，GARCH-skewed-t，GARCH-skewed-GED等存在较明显的风险高估，这表明基于GED，skewed-t与skewed-GED分布的GARCH模型生成的分布尾部过厚；2）从空头VaR来看，除GARCH-skewed-t外所有模型均能有效估计95%置信水平下的空头VaR.GARCH-GED，GARCH-skewed-GED存在明显的风险高估.在所有模型中，基于混合分布的VaR估计方法有最小的估计误差；3）除基于混合分布的VaR估计方法，GARCH-skewed-t，GARCHGED与GARCH-skewed-GED外，其他模型均无法有效估计99%置信水平下的空头VaR，未通过似然比检验，不同程度低估了股指期货空头尾部风险，为无效的估计方法.基于厚尾分布的GARCH模型在估计空头尾部风险时有较好的效果.综合来看，本文提出的基于混合分布的VaR估计方法相较其他模型更好.该方法估计股指期货空头VaR更为准确，在多头VaR与空头VaR上有较为均衡的估计能力.与GARCH-GED模型为所有模型中仅有的两个没有出现失效情况的模型（GARCH-GED模型估计的多头VaR误差较大）.

从图3可以看出，方差—协方差法的动态调整能力最差，GARCH-N，GARCH-t，GJR与NM-GARCH的整体估计效果较为接近.基于厚尾分布的GARCH模型（GARCH-GED，GARCH-skewed-t，GARCH-skewed-GED）估计结果较为接近，存在较为明显的风险高估.基于混合分布的估计方法相较其他模型与方法，能够更好地根据市场的变化进行调整，较好地拟合金融收益率的非对称特征.如检验样本中第325个～第375个样本，在这一段股指期货多头风险缩小，空头风险放大.GARCH族模型未能良好拟合多头风险缩小的过程，存在高估空头风险的情况.而基于混合分布的估计方法估计出的多头VaR在减小，空头VaR在增加，良好地拟合了收益率波动的非对称变化.

4.4 其它期货品种的VaR估计

进一步的，本文选取了金属期货，能源石化期货及农产品期货中交易量较大的铜期货，橡胶期货与豆粕期货数据，对不同模型的VaR估计能力进行了稳健性检验.计算结果如表4所示（此处仅列出失败率与似然比检验的p值）.

从表4可知，1）GARCH-N与GARCH-t模型均能有效估计橡胶期货和豆粕期货的多头与空头VaR，在估计铜期货95%置信水平下的空头VaR时失效.这两种模型在估计空头VaR时存在较为明显的风险高估，空头风险估计能力较差；2）GARCH-skewed-t，GARCH-GED与GARCH-skewed-GED模型由于使用了厚尾分布假定有较强的尾部风险估计能力.在估计99%置信水平下的VaR时，除GARCH-GED模型在估计橡胶期货空头VaR时出现了失效，其它的模型在不同数据下均得到了有效的VaR估计.但是这些模型在估计95%置信水平下的VaR时存在明显的风险高估.尤其是在估计空头VaR时，除GARCH-skewed-GED模型在估计橡胶期货时得到了有效估计，其它模型均失效，没有通过似然比检验，空头风险估计能力较差；3）基于混合分布VaR估计方法是所有模型中唯一没有出现失效情况的估计方法，对于不同数据有稳定的估计能力.在估计99%置信水平下的VaR时相较其他模型有较小的估计误差，有较好的尾部风险估计能力.多头与空头VaR的估计能力较为均衡，能够较好地拟合收益率的非对称性.

表3 股指期货VaR估计效果对比Table 3 Comparison of VaR estimation results in CSI300 futures market

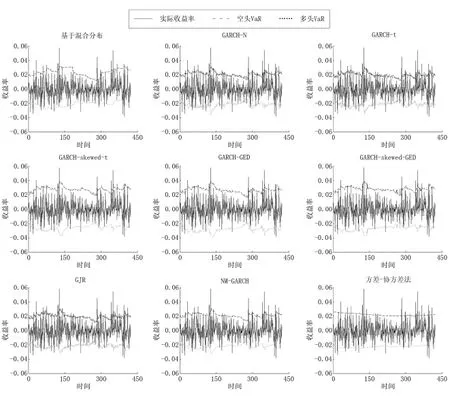
图3 不同模型95%置信水平下的VaR值与实际收益率对比Fig.3 Comparison between VaR and return of different models at 95%confidence

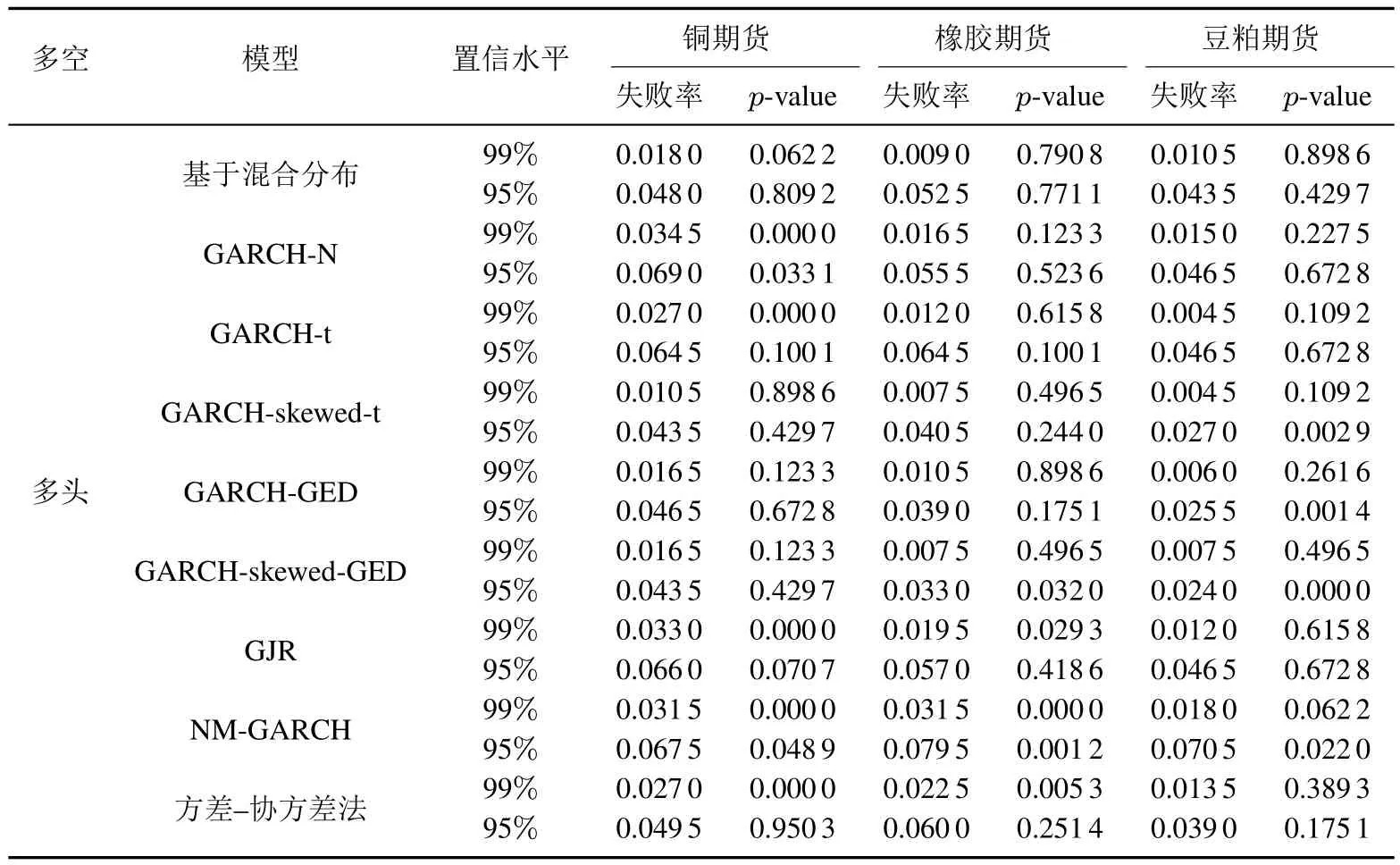
表4 多品种期货VaR估计效果对比Table 4 Comparison of VaR estimation results in several futures markets

续表4Table 4 Continue

5 结束语

现有的VaR估计方法大部分将收益率的母体分布看做单一分布.然而这种思路忽视了金融市场存在不同状态.本文将收益率的母体分布看作混合分布，使用非参数方法对股指期货，铜期货，橡胶期货与豆粕期货在99%与95%两个置信水平下的多头VaR与空头VaR进行计算，并与传统的GARCH-N模型，GARCH-t模型，GJR模型，基于厚尾分布的GARCH模型（GARCH-GED，GARCH-skewed-t，GARCH-skewed-GED），混合正态GARCH模型与方差—协方差法进行了比较.实证结果表明：基于厚尾分布的GARCH模型能够较好地估计尾部风险，但是在95%置信水平下估计的VaR存在明显的风险高估.基于混合分布的非参数VaR估计方法相较其他模型有更好的空头VaR估计能力，估计尾部风险更准确，对于不同类型的数据有稳定的估计效果.由于使用了非参数方法估计子分布，该方法能够较好拟合金融收益率分布的非对称与高峰厚尾特征，是一种有效的VaR估计方法.

［1］Morgan J P.Creditmetrics-technical Document.New York：JP Morgan，1997.

［2］Jorion P.Value at Risk：The New Benchmark for Controlling Market Risk.New York：McGraw-Hill，1997：17.

［3］Artzner P，Delbaen F，Eber J M，et al.Coherent measures of risk.Mathematical Finance，1999，9（3）：203—228.

［4］Lamoureux C G，Lastrapes W D.Heteroskedasticity in stock return data：Volume versus GARCH effects.The Journal of Finance，1990，45（1）：221—229.

［5］Haan W J，Spear S A.Volatility clustering in real interest rates theory and evidence.Journal of Monetary Economics，1998，41（3）：431—453.

［6］Campbell J Y，Hentschel L.No news is good news：An asymmetric model of changing volatility in stock returns.Journal of Financial Economics，1992，31（3）：281—318.

［7］Angelidis T，Benos A，Degiannakis S.The use of GARCH models in VaR estimation.Statistical Methodology，2004，1（1）：105—128.

［8］So M K P，Yu P L H.Empirical analysis of GARCH models in value at risk estimation.Journal of International Financial Markets，Institutions and Money，2006，16（2）：180—197.

［9］王美今，王 华.基于GARCH-t的上海股票市场险值分析.数量经济技术经济研究，2002（3）：106—109. Wang M J，Wang H.Analysis for VaR of Shanghai stock market based on GARCH-t model.The Journal of Quantitative&Technical Economics，2002（3）：106—109.（in Chinese）

［10］陈守东，俞世典.基于GARCH模型的VaR方法对中国股市的分析.吉林大学社会科学学报，2002（4）：11—17. Chen S D，Yu S D.Analysis of China's stock market using VaR method based on GARCH model［J］.Jilin University Journal Social Sciences Edition，2002（4）：11—17.（in Chinese）

［11］刘庆富，仲伟俊，华仁海，等.EGARCH-GED模型在计量中国期货市场风险价值中的应用.管理工程学报，2007，21（1）：117—121. Liu Q F，Zhong W J，Hua R H，et al.Application of EGARCH-GED model for calculating value at risk in chinese futures market. Journal of Industrial Engineering and Engineering Management，2007，21（1）：117—121.（in Chinese）

［12］Su E，Knowles T W.Asian pacific stock market volatility modeling and value at risk analysis.Emerging Markets Finance and Trade，2006，42（2）：18—62.

［14］Orhan M，K¨oksal B.A comparison of GARCH models for VaR estimation.Expert Systems with Applications，2012，39（3）：3582—3592.

［15］林 宇，魏 宇，黄登仕.基于GJR模型的EVT动态风险测度研究.系统工程学报，2008，23（1）：45—51. Lin Y，Wei Y，Huang D S.Study on dynamic risk measurement based on GJR and EVT.Journal of Systems Engineering，2008，23（1）：45—51.（in Chinese）

［16］Longin F M.From value at risk to stress testing：The extreme value approach.Journal of Banking&Finance，2000，24（7）：1097—1130.

［17］McNeil A J，Frey R.Estimation of tail-related risk measures for heteroscedastic financial time series：An extreme value approach. Journal of Empirical Finance，2000，7（3）：271—300.

［18］Hendricks D.Evaluation of value-at-risk models using historical data.Economic Policy Review，1996，2（1）：39—69.

［19］王春峰，万海辉，李 刚.基于MCMC的金融市场风险VaR的估计.管理科学学报，2000，3（2）：54—61. Wang C F，Wan H H，Li G.Esimation of value-at-risk using MCMC.Journal of Management Sciences in China，2000，3（2）：54—61.（in Chinese）

［20］尹优平，马 丹.基于分布拟合方法的高频数据风险价值研究.金融研究，2005（3）：59—67. Yin Y P，Ma D.Analysis for VaR of high-frequency data based on distribution fitting method.Journal of Financial Research，2005（3）：59—67.（in Chinese）

［21］叶五一，缪柏其，吴振翔.基于Bootstrap方法的VaR计算.系统工程学报，2004，19（5）：528—531. Ye W Y，Miao B Q，Wu Z X.Bootstrap method based evaluating VaR.Journal of Systems Engineering，2004，19（5）：528—531.（in Chinese）

［22］Efron B.Bootstrap methods：Another look at the jackknife.The Annals of Statistics，1979，7（1）：1—26.

［23］Kupiec，Paul H.Techniques for verifying the accuracy of risk measurement models.The Journal of Derivatitves，1995，3（2）：73—84.

Estimating VaR by nonparametric estimation with mixed distribution：Empirical investigation of futures market

Xiao Jiawen，Yang Zheng
（School of Management and Economics，University of Electronic Science and Technology of China，Chengdu 611731，China）

This paper proposes a new nonparametric estimation method for the VaR（value at risk）based on a mixed distribution.This method classifies market states as the stationary state and trend or fluctuating state via market changes and assumes the distribution of the asset return to be a mixed distribution.It classifies the market states using high-frequency daily data，estimates sub-distributions using kernel density estimation based on Bootstrap method，and computes the total VaR at last.CSI300，copper，rubber and soybean meal futures were selected to estimate the VaR of both long and short positions at different confidence levels in the empirical study.The empirical results show that the new method can estimate the VaR of short positions and tail risks more accurately than GARCH-type models，GARCH models based on fat tail assumptions，NM-GARCH model and variance-covariance method.

VaR；mixed distribution；kernel density estimation；Bootstrap

F830.91

A

1000-5781（2016）04-0471-10

10.13383/j.cnki.jse.2016.04.005m

肖佳文（1990—），男，湖北十堰人，硕士，研究方向：金融风险度量方法，Email：jiawen.xiao@hotmail.com；

2014-03-03；

2014-10-09.

国家自然科学基金资助项目（70901013）；教育部人文社会科学研究青年基金资助项目（15YJC790132）；中央高校基本科研业务费资助项目（ZYGX2015J159）.

杨 政（1978—），男，四川安岳人，博士，副教授，研究方向：金融时间序列分析，Email：yangzheng@uestc.edu.cn.